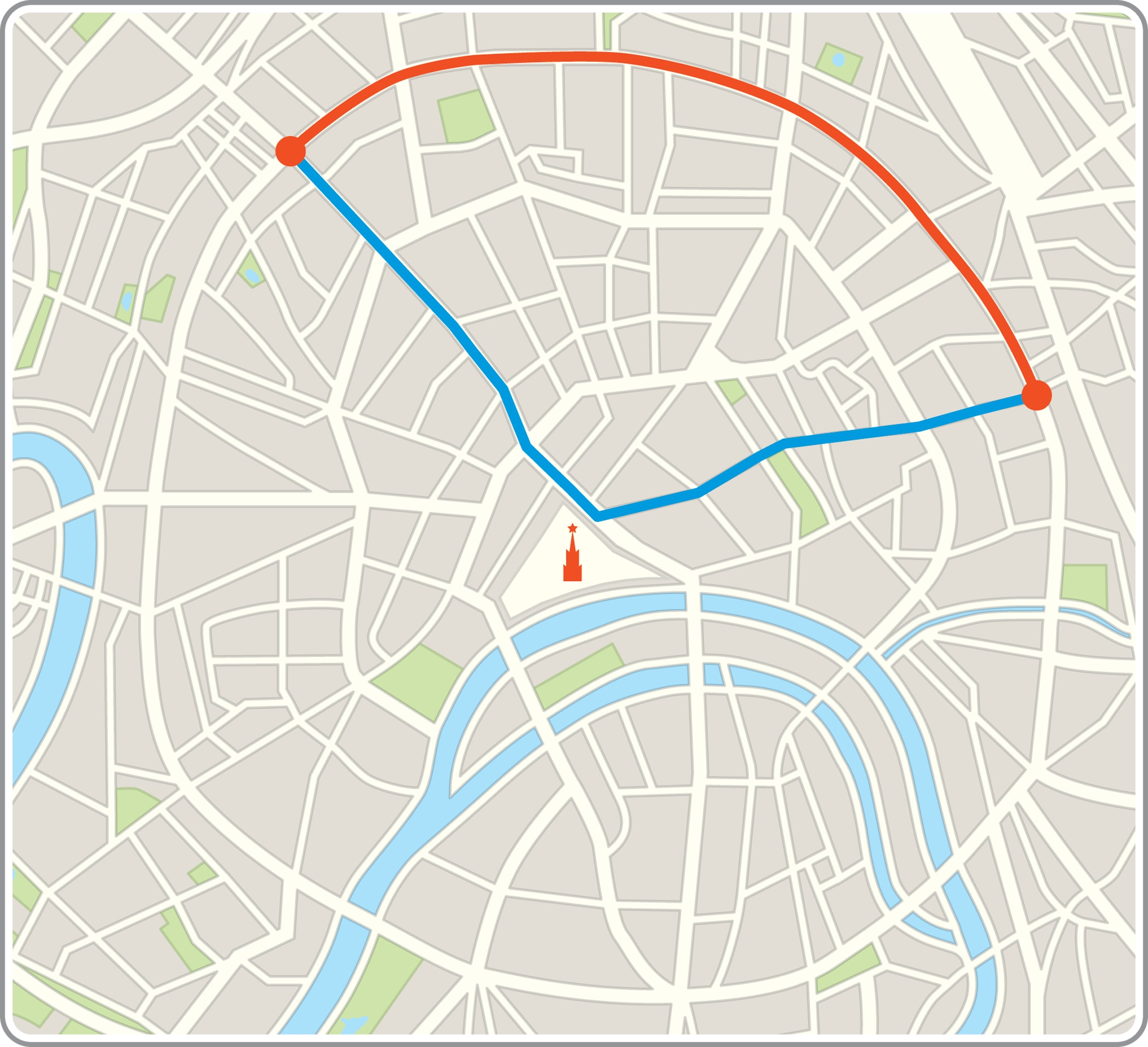
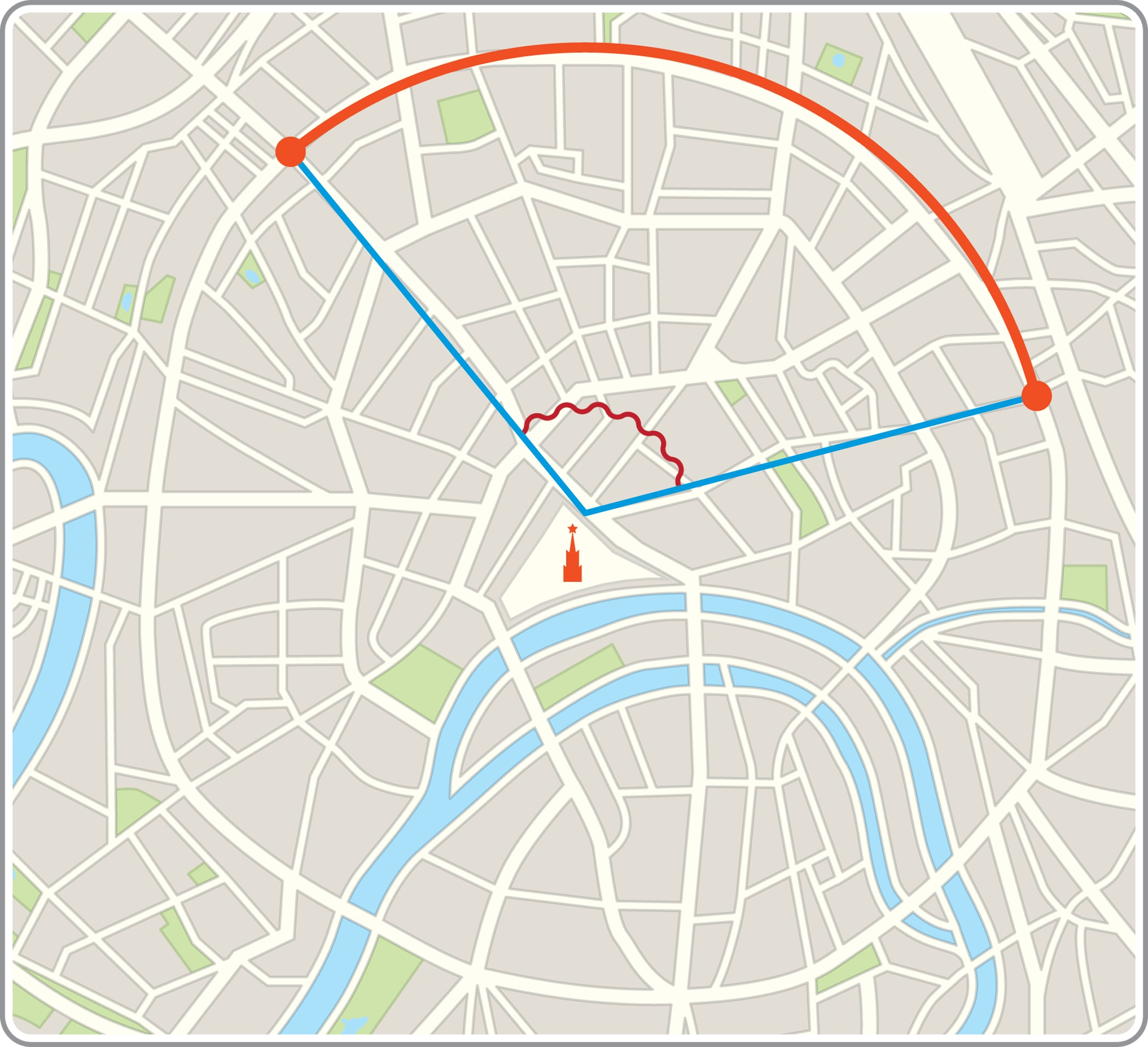
Вы хотите прогуляться по Москве. Какой путь от станции метро «Маяковская» до станции «Курская» короче: по Садовому кольцу или через центр, через Красную площадь?
Рассмотрим математическую модель. Вы находитесь в городе с сетью радиальных и кольцевых дорог. Какой путь между точками, расположенными на одном кольце, является самым коротким?
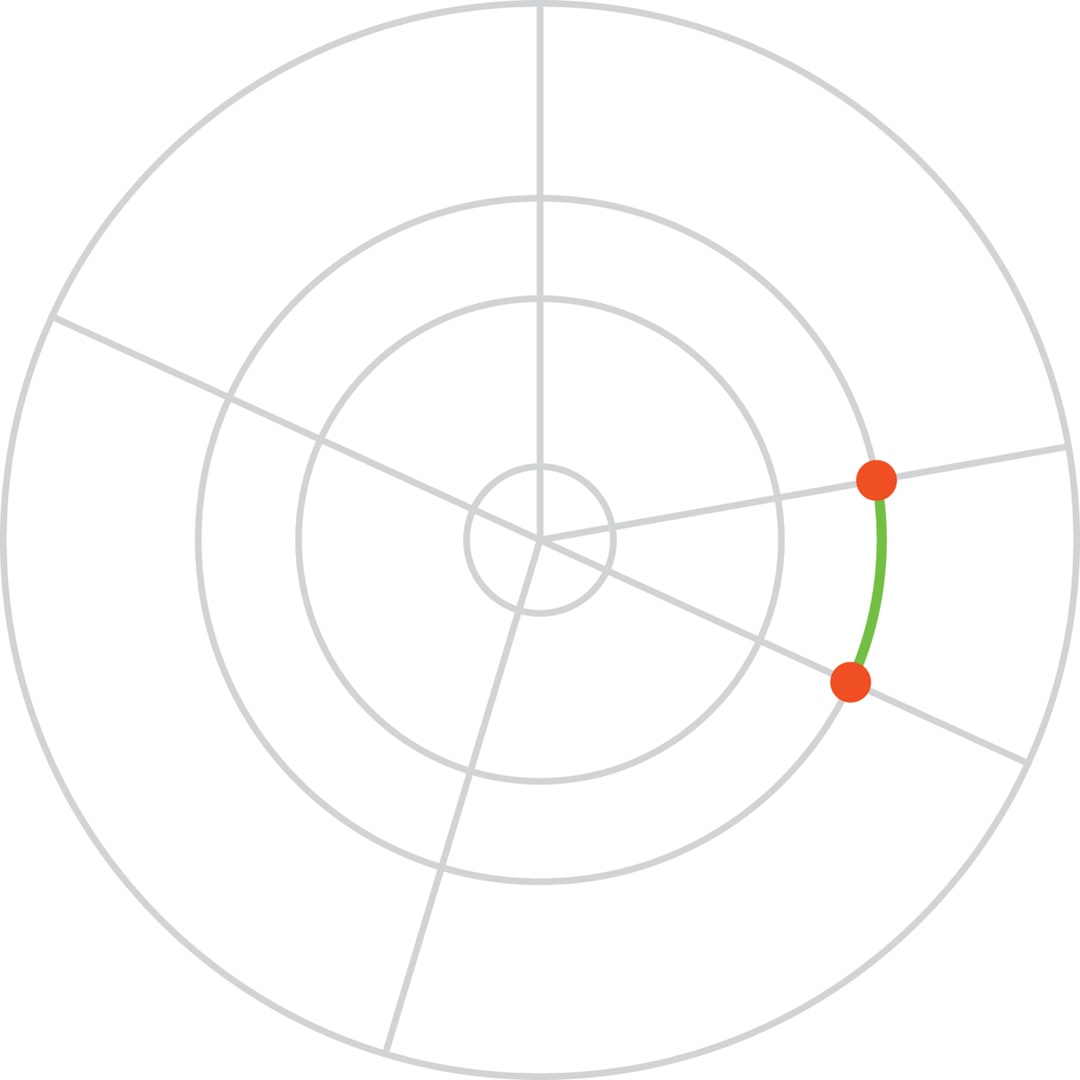
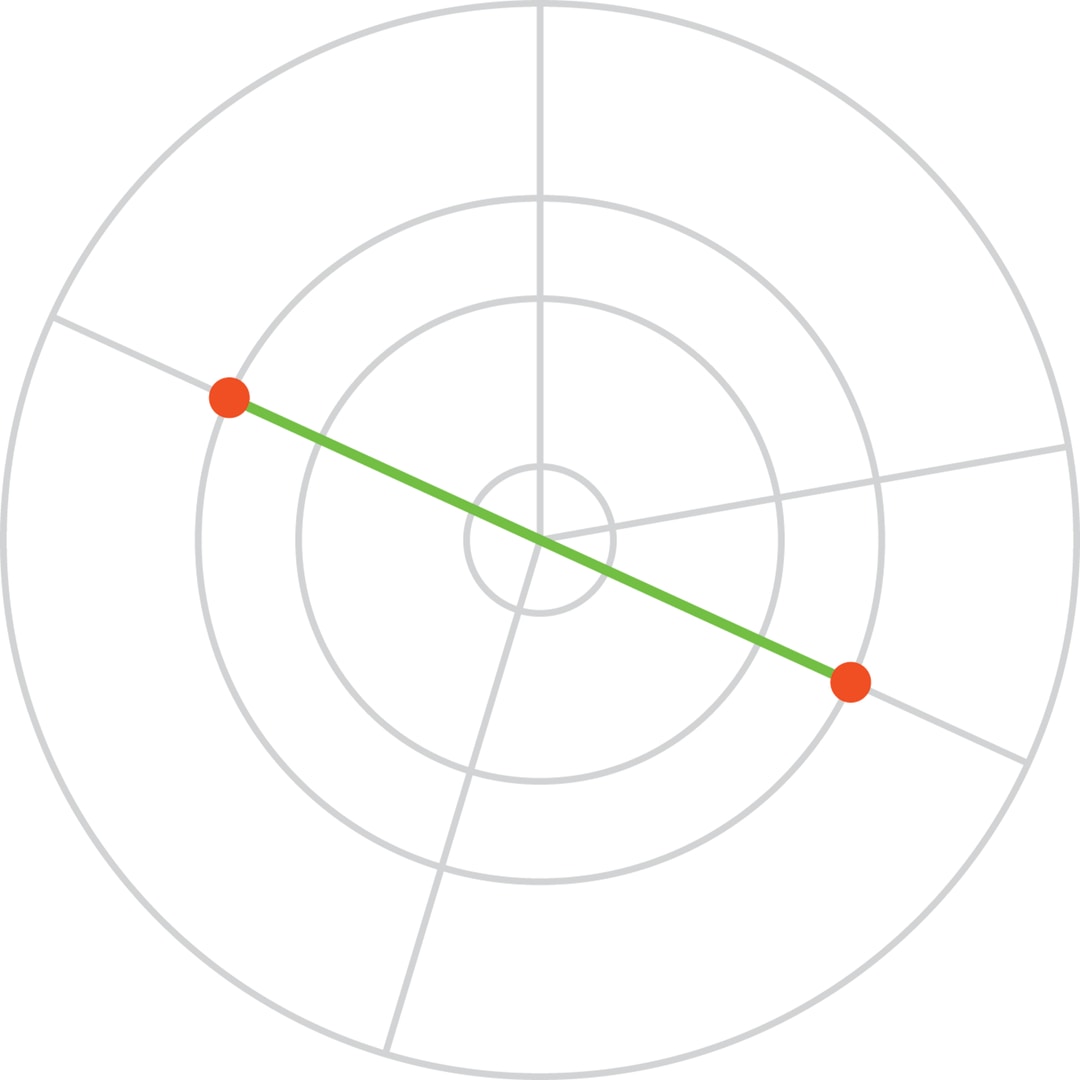
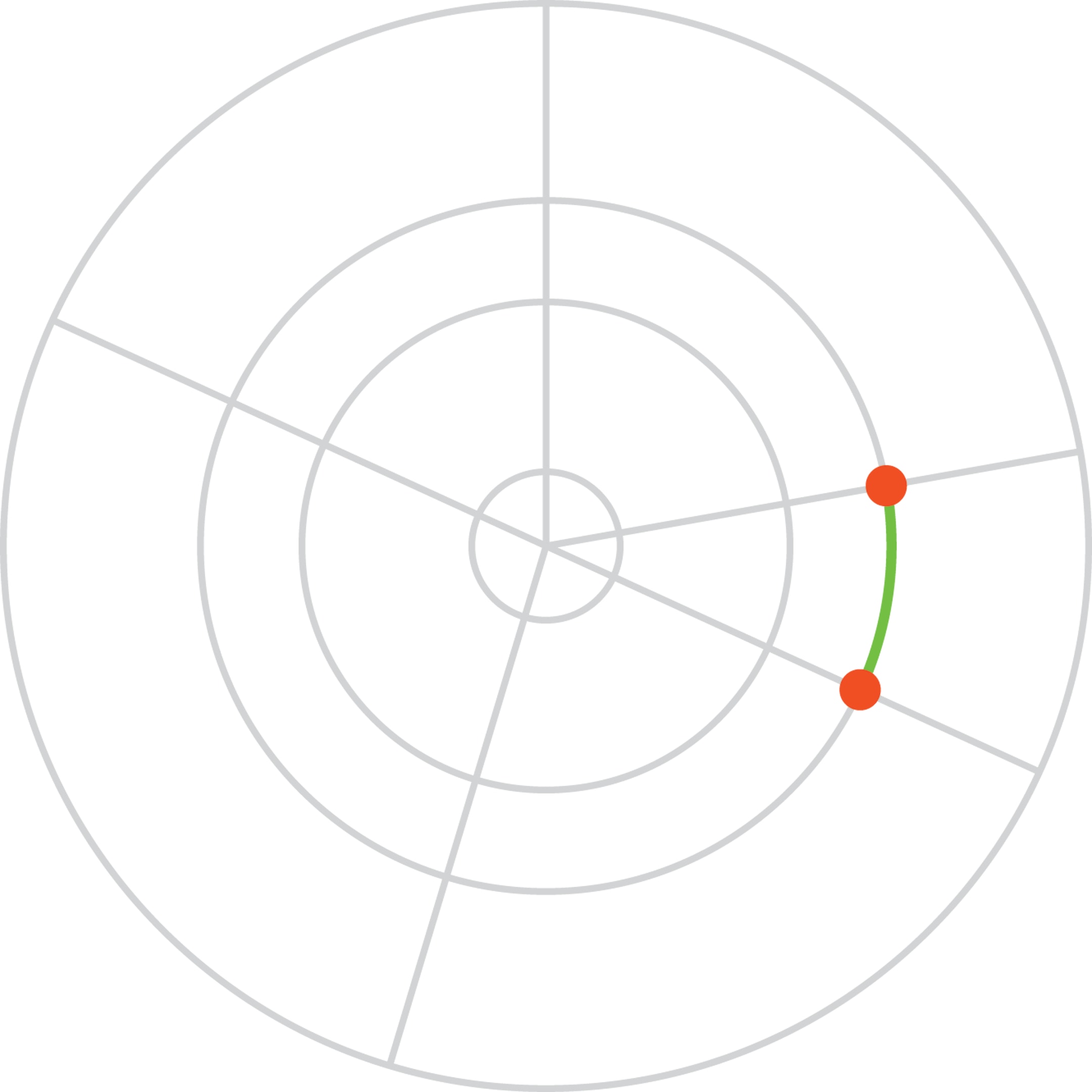
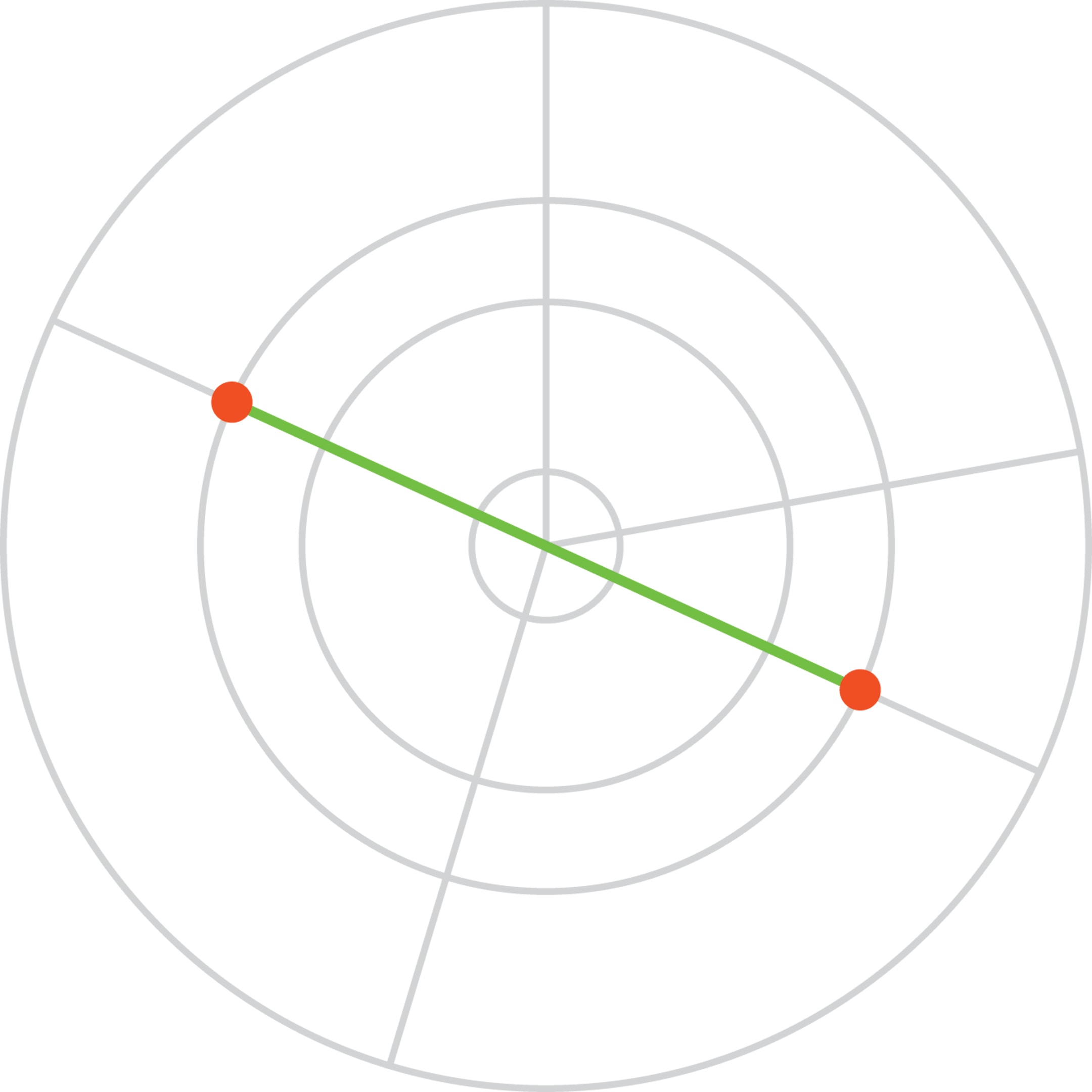
Если точки достаточно близки друг к другу, то наиболее короткий путь — по кольцевой дороге. Если точки диаметрально противоположны друг другу, то наиболее короткий путь — по радиальным дорогам, поскольку кратчайшим путём между двумя точками является отрезок прямой.
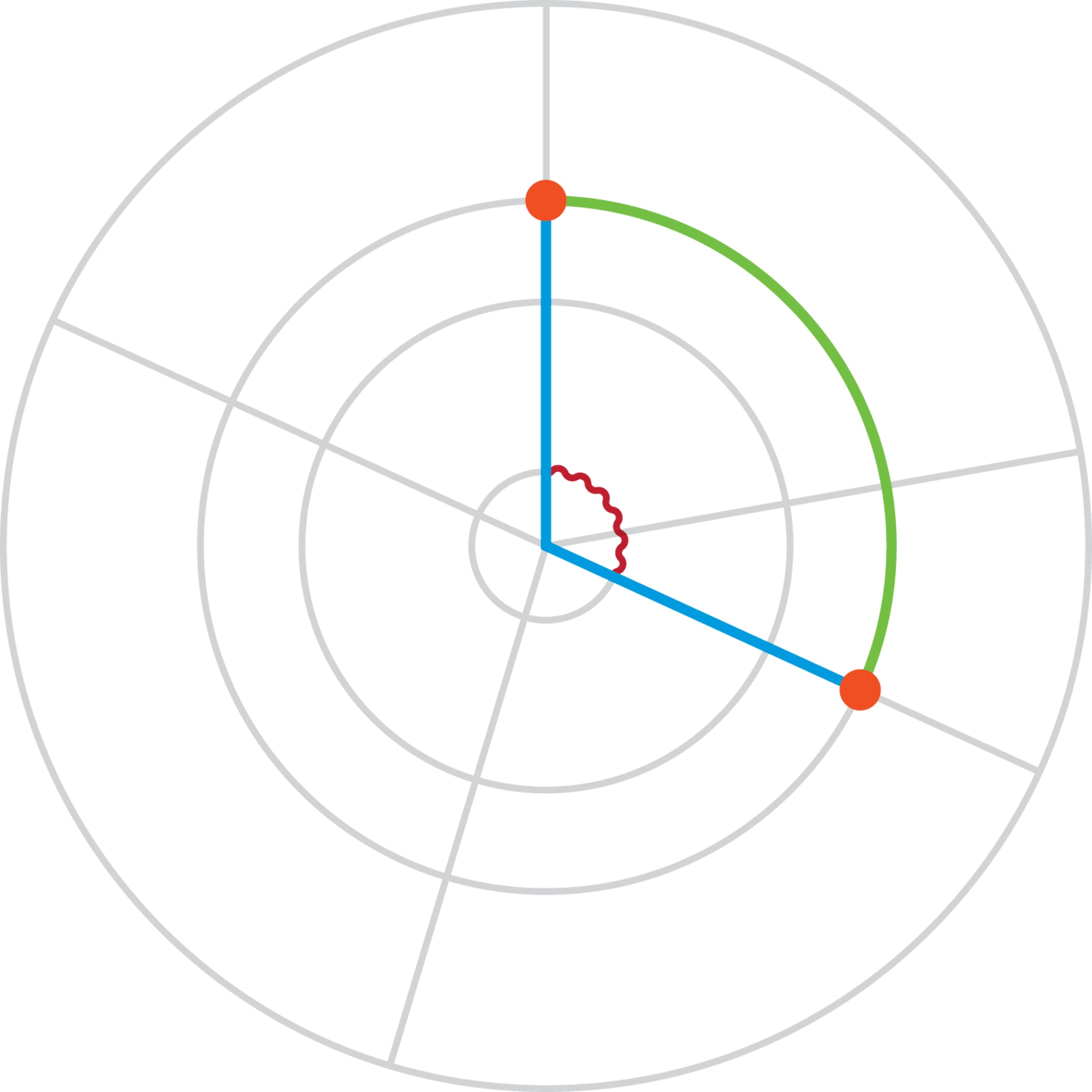
По здравому смыслу (из соображений непрерывности) можно ожидать, что при некотором положении точек длина путей будет одинаковой. Это действительно так, если угол между радиусами равен 2 радианам (примерно 115 градусов).
С хорошей точностью длина пути между указанными станциями метро по Садовому кольцу равна длине пути через Красную площадь.
В наших рассуждениях вывод не зависел от радиуса окружности, на которой находятся точки, что объясняется подобием круговых секторов с общим центром и одинаковым центральным углом.
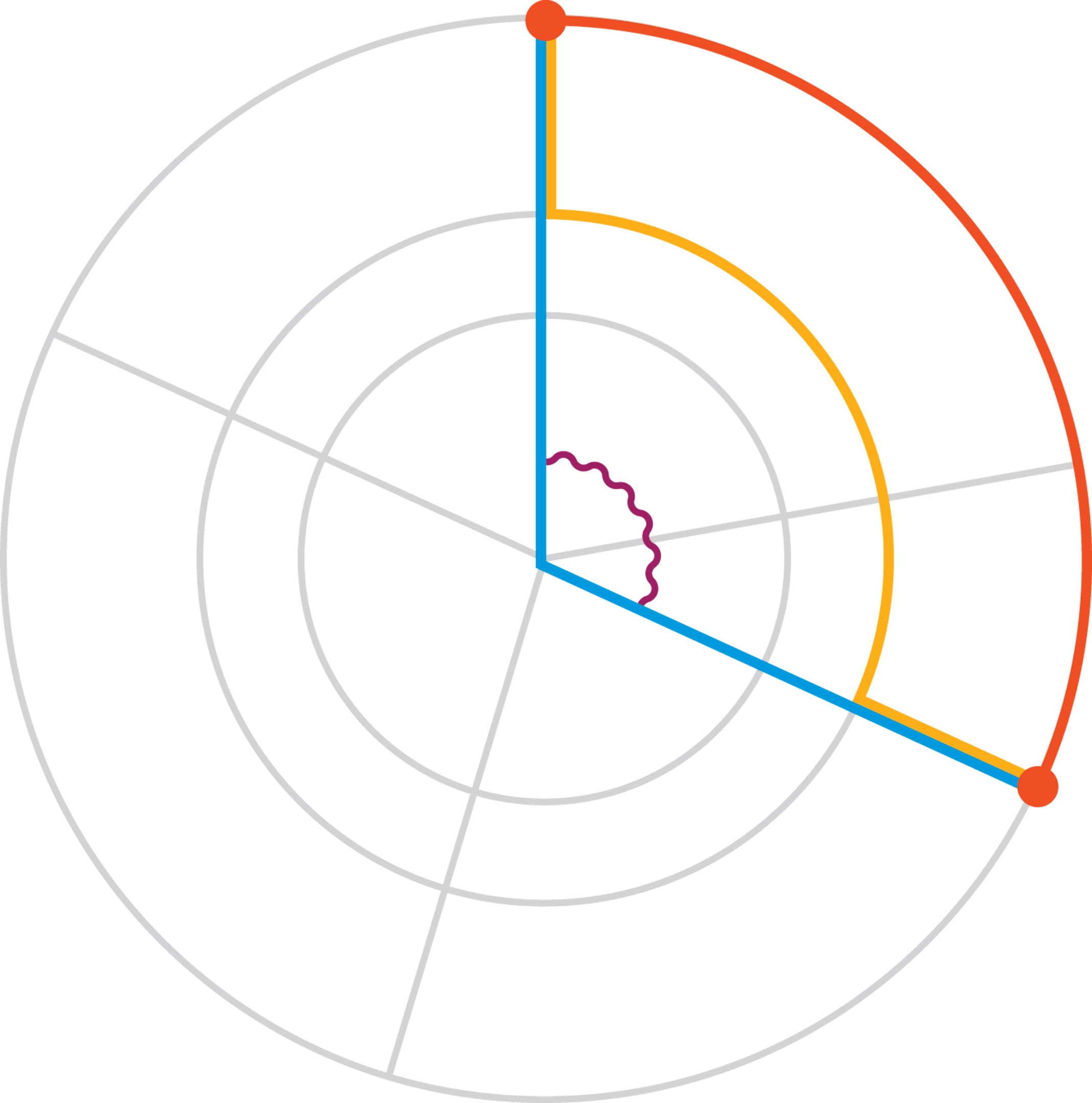
Например, если угол между радиусами двух точек на МКАД равен 2 радианам, то, выбирая автомобильный маршрут, можно просто поехать по кольцевой дороге, можно проехать по радиусам через центр, а можно и комбинировать — проехать по радиусу до Третьего транспортного кольца, потом — по дуге этого кольца до радиуса второй точки, затем вернуться по радиусу на МКАД. Длины всех рассмотренных маршрутов являются одинаковыми.
Радиально-кольцевая планировка Москвы сложилась исторически: город разрастался вокруг Кремля «вековыми кольцами», во внешний мир уходили магистральные дороги в виде лучей, получавшие свои названия по тем городам, монастырям и даже странам, к которым они вели. Например, Тверская улица шла к Твери (некогда — сопернице Москвы), а позднее стала началом главной дороги к Северной столице, Санкт-Петербургу. Пречистенка вела к Новодевичьему монастырю, где хранилась икона Пречистой Божией Матери Смоленской, а Большая Ордынка — в Золотую Орду.
Главные кольцевые дороги старой Москвы — Бульварное кольцо и Садовое кольцо — возникли на месте снесённых стен и укреплений, утративших военное значение: стен Белого города и Земляного вала соответственно.
Ещё один пример радиально-кольцевой планировки в нашей стране — Софийская сторона Новгорода. В Европе многие столицы возникали на месте старых крепостей и сохранили порождённую этим обстоятельством радиальную структуру, яркие образцы — Вена и Париж.
С появлением метро радиально-кольцевые структуры стали уходить и под землю. И если в Москве схема метрополитена стала проекцией линий наземных дорог, то в других случаях радиально-кольцевые схемы метро возникали вне связи с тем, что происходило «наверху», пример — метро в Мадриде.
Радиан — это центральный угол, опирающийся на дугу окружности, длина которой равна её радиусу. Происхождение термина «радиан» связано с радиусом круга; radius в латыни — спица в колесе, луч. В математической литературе термин «радиан» появился только в XIX веке, хотя сам способ измерения углов был известен и ранее. Например, радианное измерение углов использовал Леонард Эйлер, выводя знаменитую формулу $e^{iπ}+1=0$. В данном сюжете само определение радиана становится инструментом решения задачи о пешеходной прогулке от «Маяковской» до «Курской» по разным маршрутам.