Слово «расстояние» встречается там, где необходимо измерить, представить в виде числа степень близости объектов. Расстояние может быть как обычным географическим, так и длиной отрезка на некоторой шкале: сравниваемыми характеристиками могут быть время, вес, площадь, объём и т. п.
Иногда приходится оценивать взаимную удалённость объектов в нескольких шкалах. Например, жители мегаполисов часто измеряют расстояния не только в километрах, но и в минутах и часах, которые надо потратить, чтобы добраться от одного места до другого. Впрочем, идея измерения пути временем движения по нему встречалась ещё в Древнем мире: фарсанг — это расстояние, которое может пройти за час пеший воин или верблюд в караване, примерно 5—6 км.
Но даже «географическое» расстояние можно понимать по-разному: и формально, «по карте», и как длину наименьшего реального пути. Надо не только уточнять значения слов «близко» и «далеко» в каждом конкретном случае, но и сформулировать общие требования к понятию «расстояние».
Разберём несколько способов определения расстояния между точками плоскости, каждое из которых имеет практическое применение.
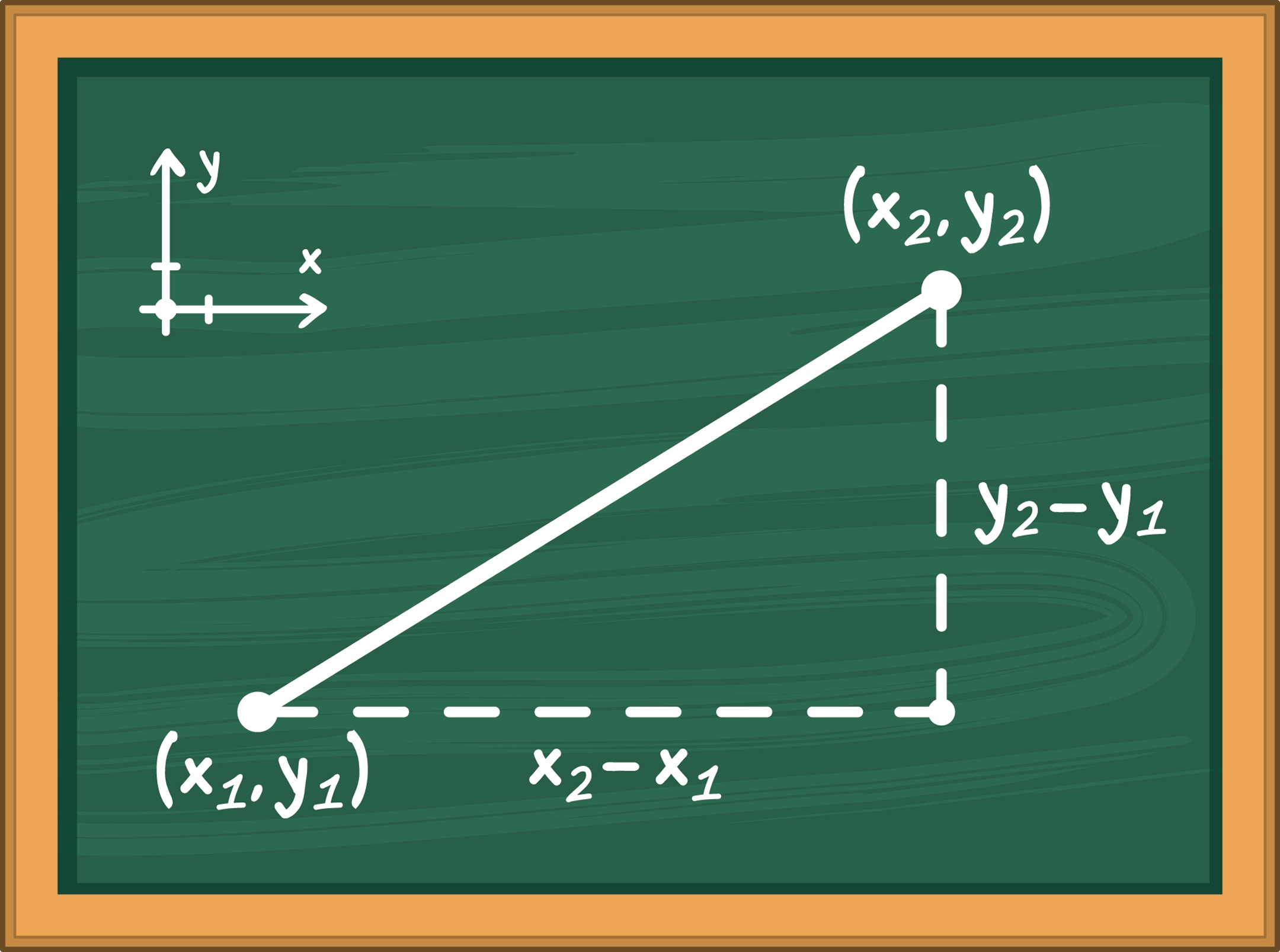
На координатной плоскости каждая точка определяется парой координат $(x;y)$. Формула $$ d(A, B)=\textstyle\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} $$
выражает обычное евклидово расстояние между точками $A(x_1;y_1)$ и $B(x_2; y_2)$. Житейски это соответствует возможности отправиться из $A$ в $B$ по кратчайшему пути — по прямой.
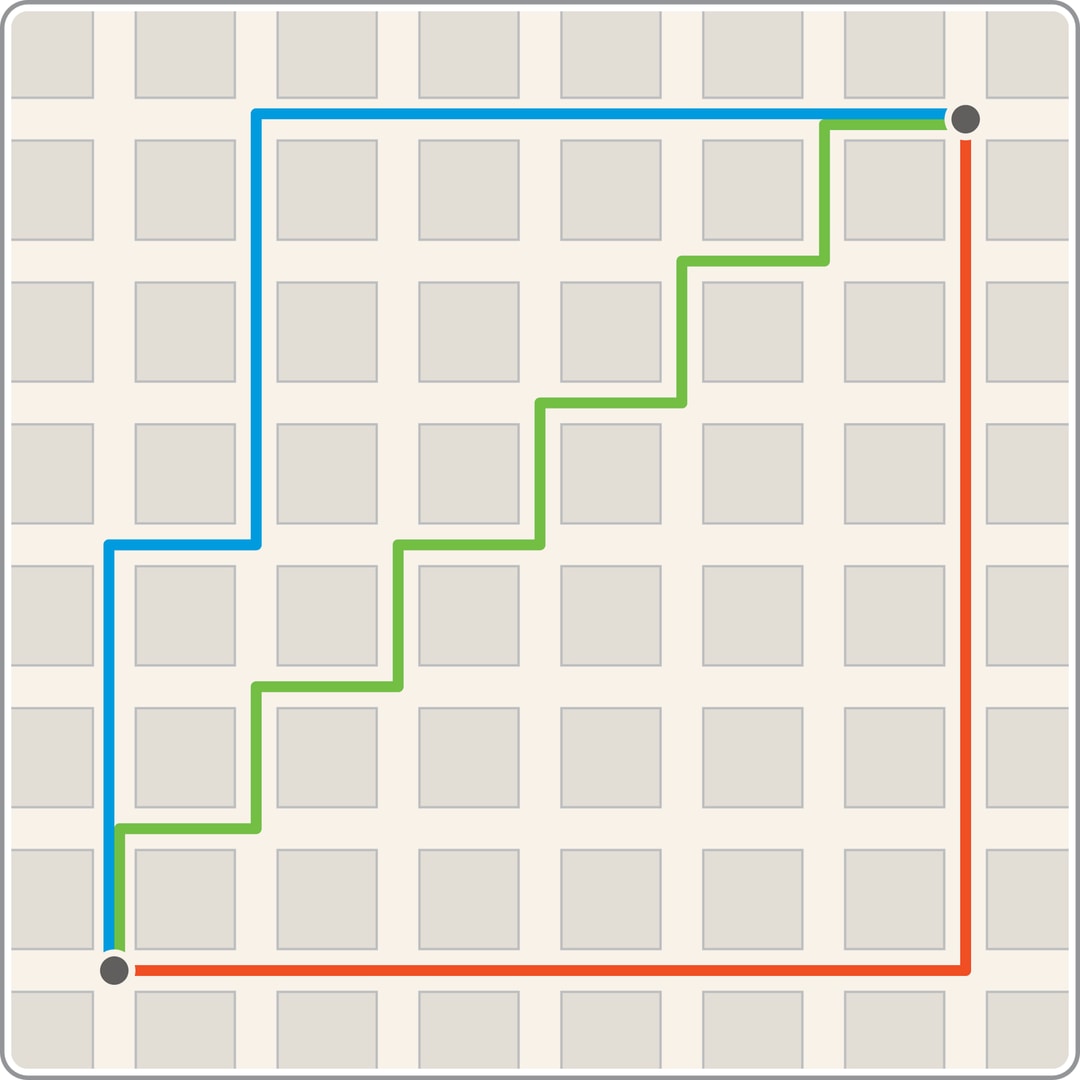
Но так можно передвигаться в море или в степи, а вот в городе столь беззаботно перемещаться уже не получится — главные маршруты пролегают по улицам. Если кварталы образуют квадратную решётку, то естественным образом возникает «расстояние городских кварталов» (его ещё называют манхэттенским, по соответствию планировке района Нью-Йорка). Оно определяется наименьшим числом кварталов, которые придётся пройти, двигаясь из одной точки (перекрёстка) в другую. В отличие от евклидова, манхэттенское расстояние между двумя точками реализуется различными ломаными, кратчайший путь — не единственный. Точки, «по манхэттенскому счёту» равноудалённые от данной, с точки зрения евклидова расстояния могут не быть равноудалёнными от неё.
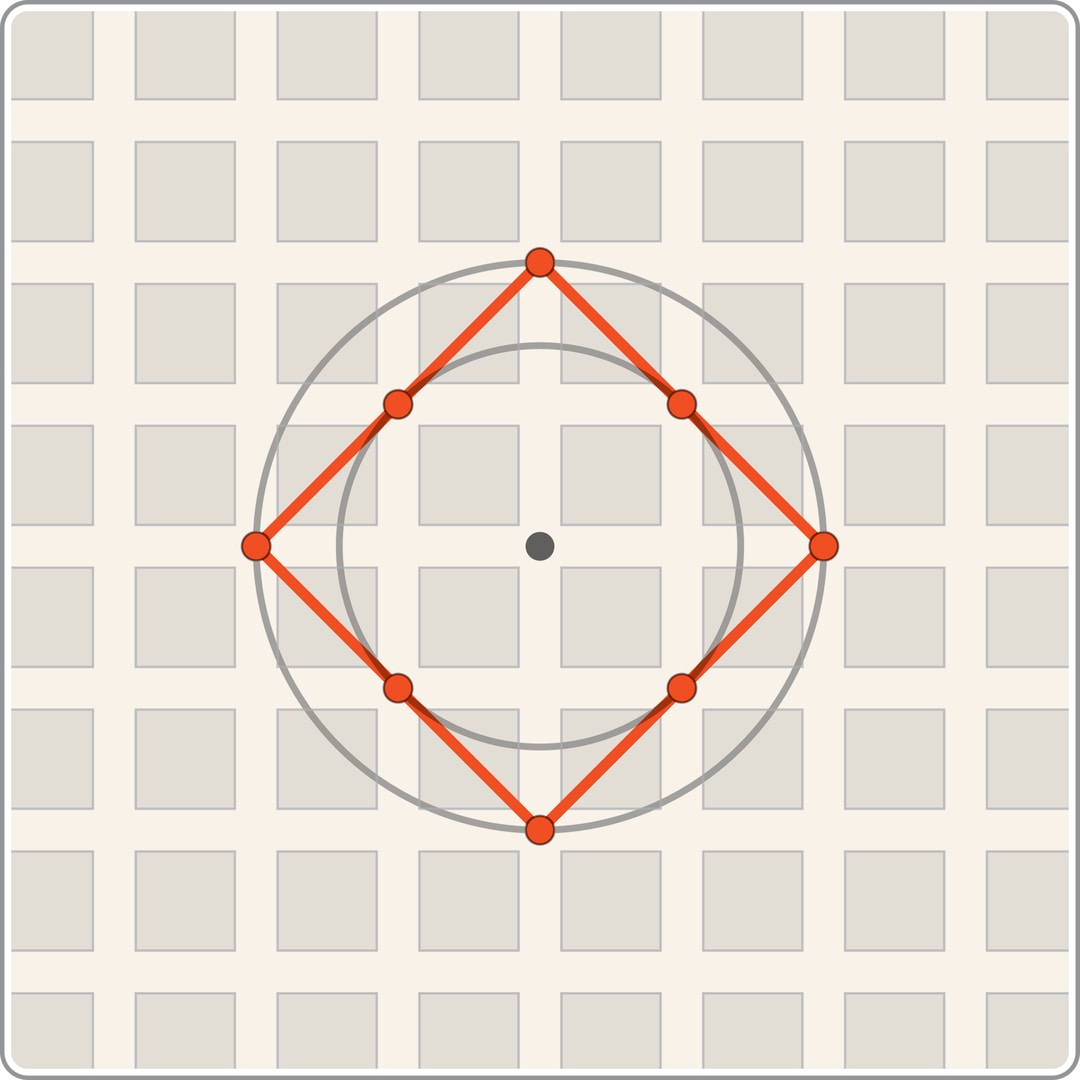
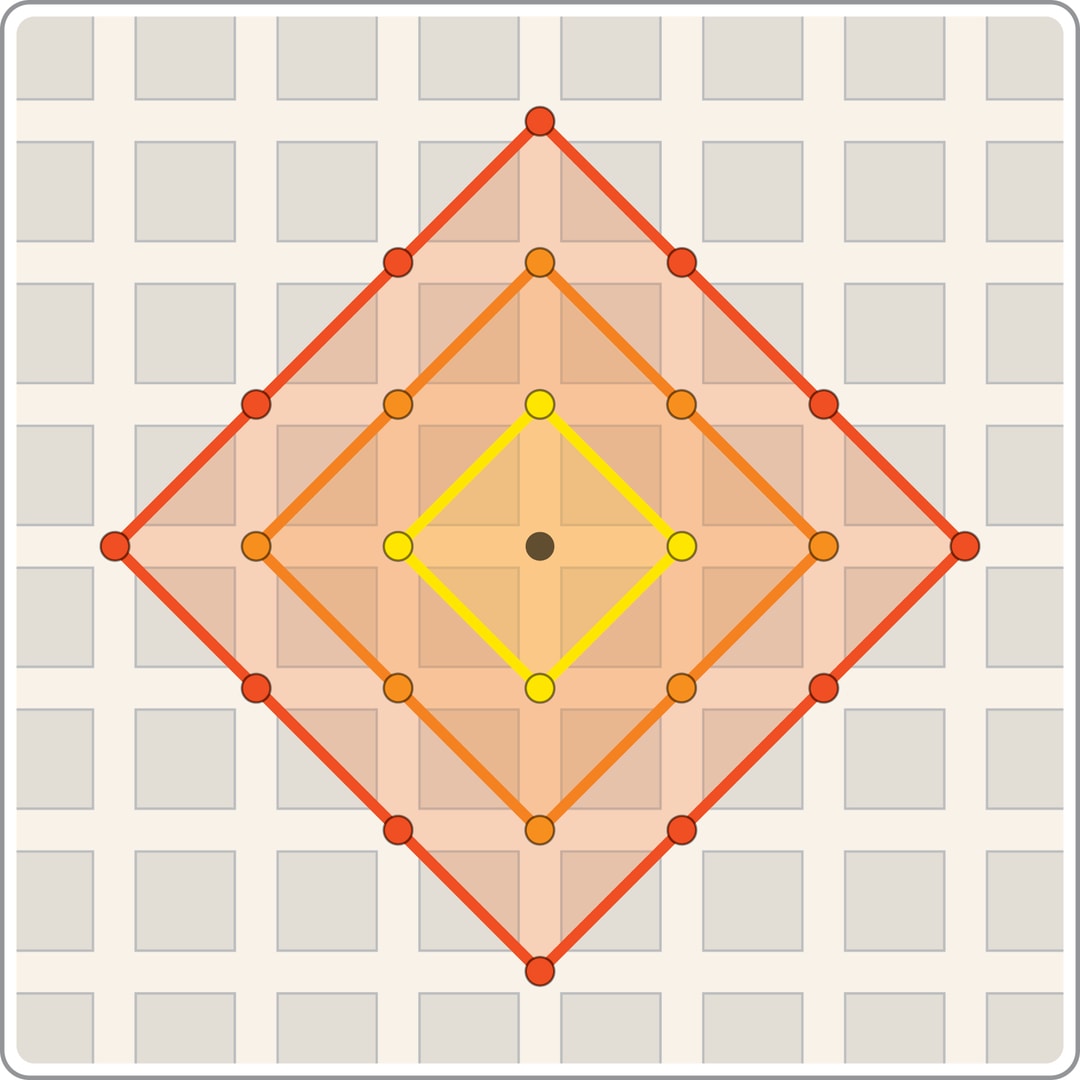
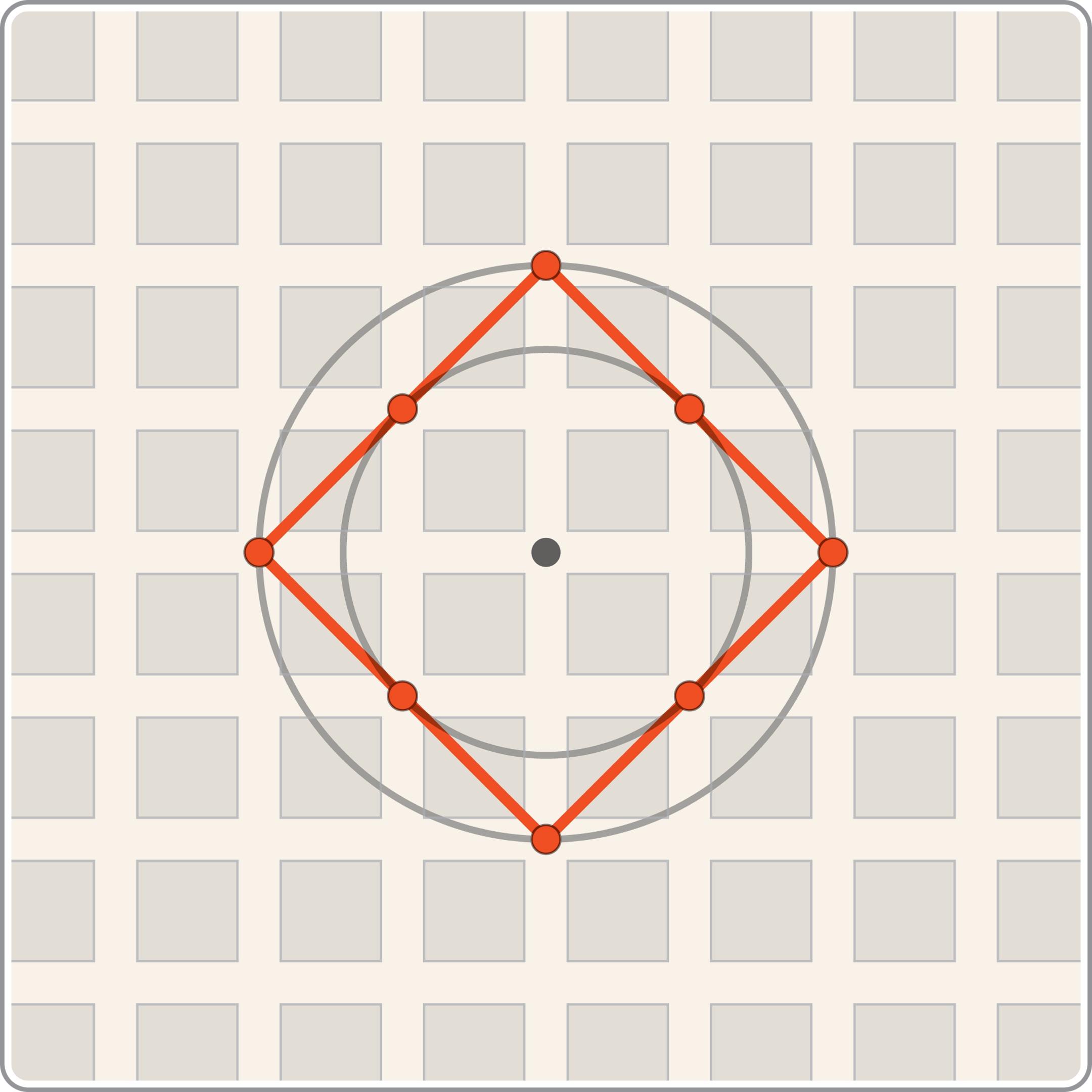
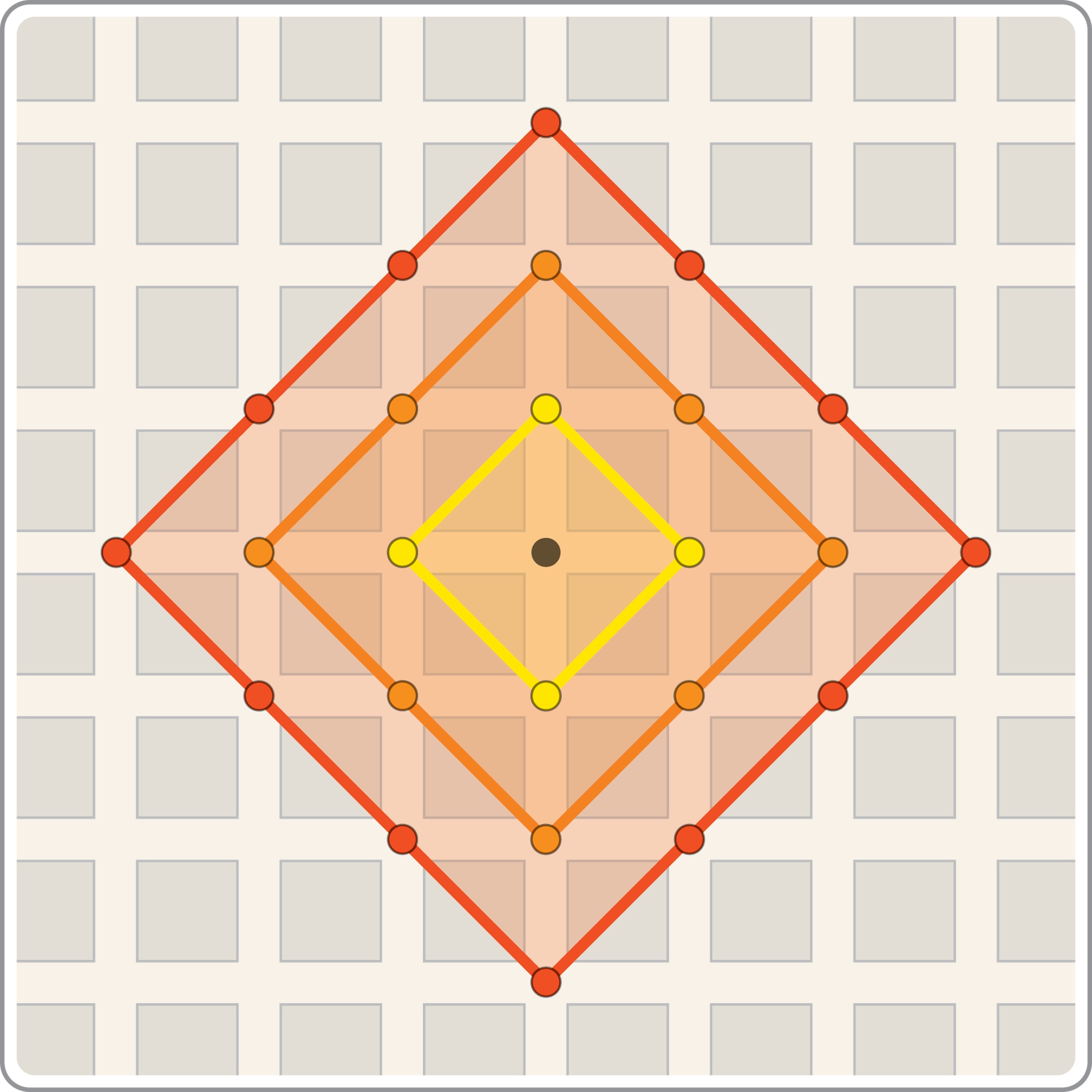
Если для выбранного расстояния назвать шаром множество точек, расстояния от которых до данной не превосходят $R$, то на плоскости евклидов шар — круг, а манхэттенский — квадрат $|x|+|y|\le R$. Если раздувать шар, то можно увидеть, как изменяется множество точек, до которых можно добраться за определённое число «шагов».
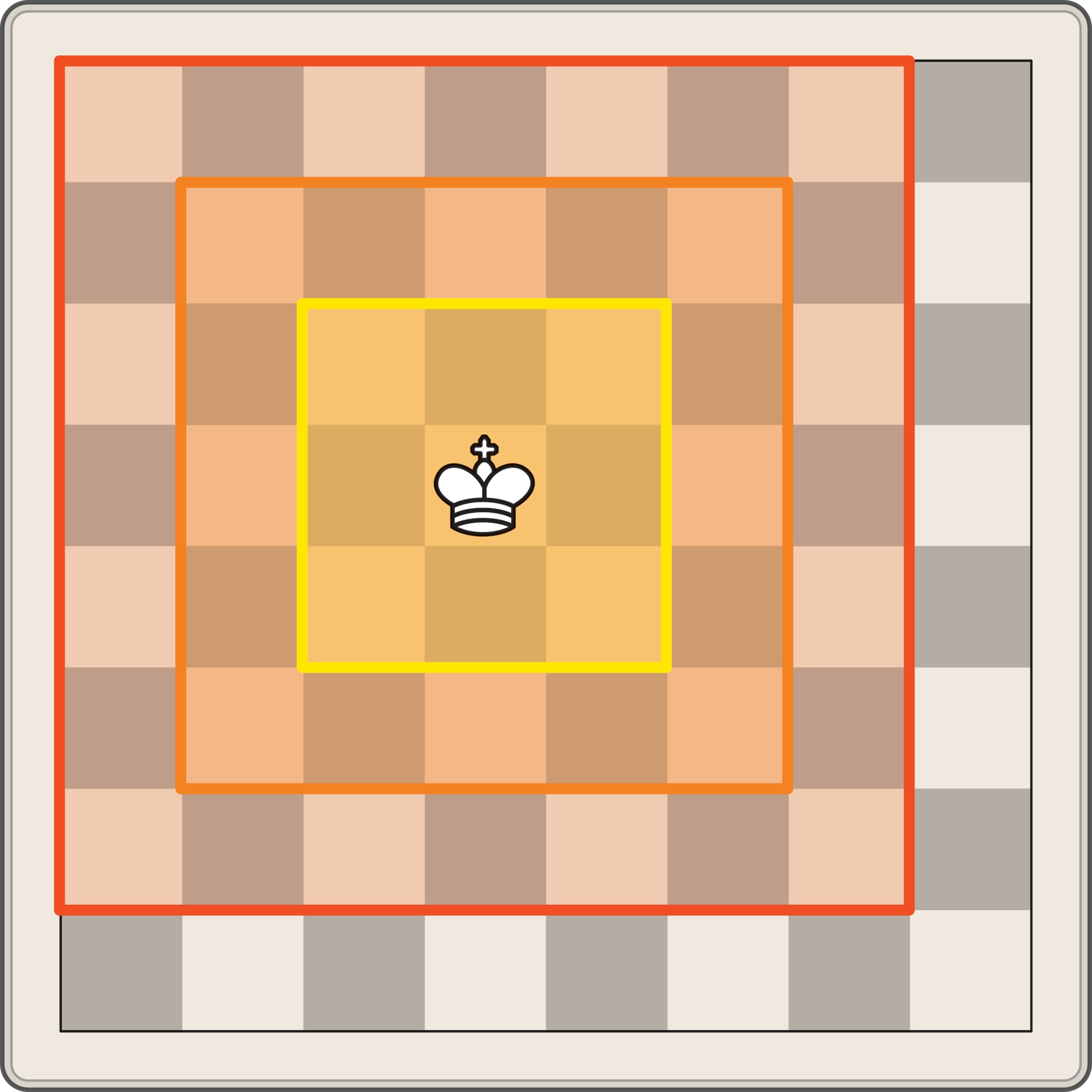
Ещё одно важное расстояние носит имя великого российского математика Пафнутия Львовича Чебышева. На шахматной доске оно связано с ходами короля. Шар — это квадрат $\max\{|x|, |y|\}\le R$.
В разобранных примерах расстояния, внешне различные, имеют следующие свойства, универсальные и естественные.
1. Неотрицательность: $d(A,B)\ge 0$, причём равенство $d(A,B)=0$ равносильно тому, что $A=B$.
2. Симметрия: $d(A,B)=d(B,A)$. Длина удава от головы до хвоста должна равняться его длине от хвоста до головы.
3. Неравенство треугольника: $d(A,B)\le d(A,C) + d(C,B)$. Если $А,B,C$ — три вершины треугольника, а расстояние — обычное евклидово, то неравенство выражает известный геометрический факт.
Перечисленные «необходимые» свойства расстояний можно превратить в определение и назвать метрическим пространством множество, в котором на каждой паре точек определена функция расстояния. Изучение свойств абстрактных метрических пространств — дело математики. Чтобы накопленными результатами воспользоваться для измерения и сравнения реальных объектов, необходимо выбрать множество, в котором эти объекты будут представлены, и ввести расстояние. Например, можно подобрать математический инструмент для сравнения фотографий так, чтобы формульная оценка «расстояние мало» совпадала с человеческой визуальной — «почти неотличимы».
В шахматах расстояние между полями измеряется длиной и формой «шага» фигуры. Так, король может двигаться по вертикалям, горизонталям и диагоналям, за один шаг — на одну клетку. Поля, на которые можно попасть, сделав не более определённого числа ходов, — это «шар» относительно такого расстояния, но этот «шар» имеет форму квадрата.
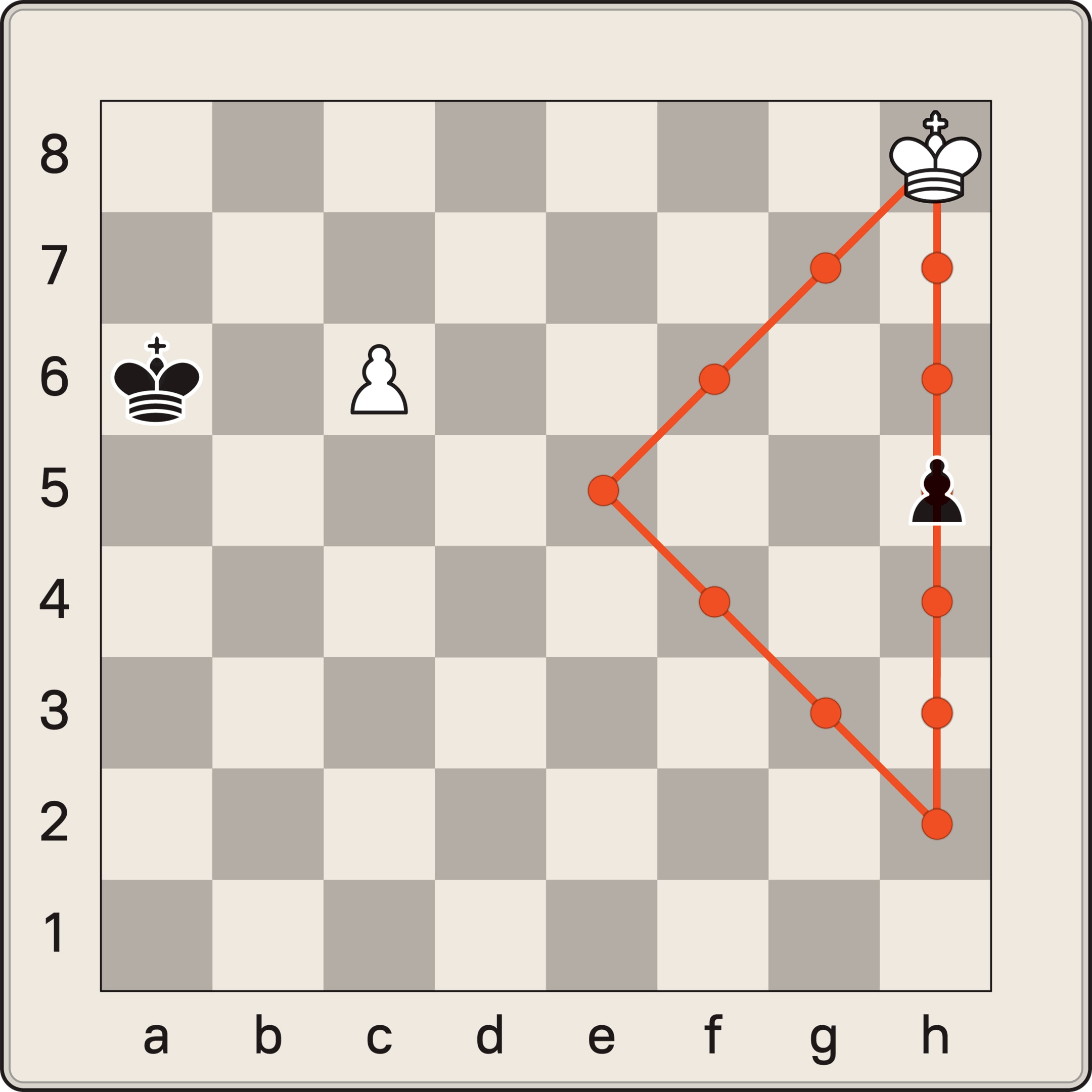
На этом непривычном, парадоксальном с бытовой точки зрения обстоятельстве основан знаменитый этюд чешского гроссмейстера Рихарда Рети, в котором задание «Ничья» кажется недостижимым результатом для белых. (В шахматных этюдах обычно начинают белые.)
В данном случае добиться ничьей белые смогут только в двух случаях: 1) если белый король догонит и съест чёрную пешку; 2) если белый король чудесным образом окажется рядом со своей пешкой и поможет ей «своевременно» превратиться в ферзя.
Геометрическая основа решения — то, что путь белого короля h8 → e5 → h2 имеет ту же «длину» (число ходов), что и «прямой» отрезок h8—h2. А достигнув поля e5, король становится не только догоняющим чёрную пешку, но и проводником, защитником собственной пешки на поле c6. И в зависимости от ходов чёрных фигур, может быть реализован первый или второй вариант достижения ничьей. (Отметим, что в одном из разветвлений белому королю с поля f6 приходится сразу отправляться через e6 на помощь своей пешке.)
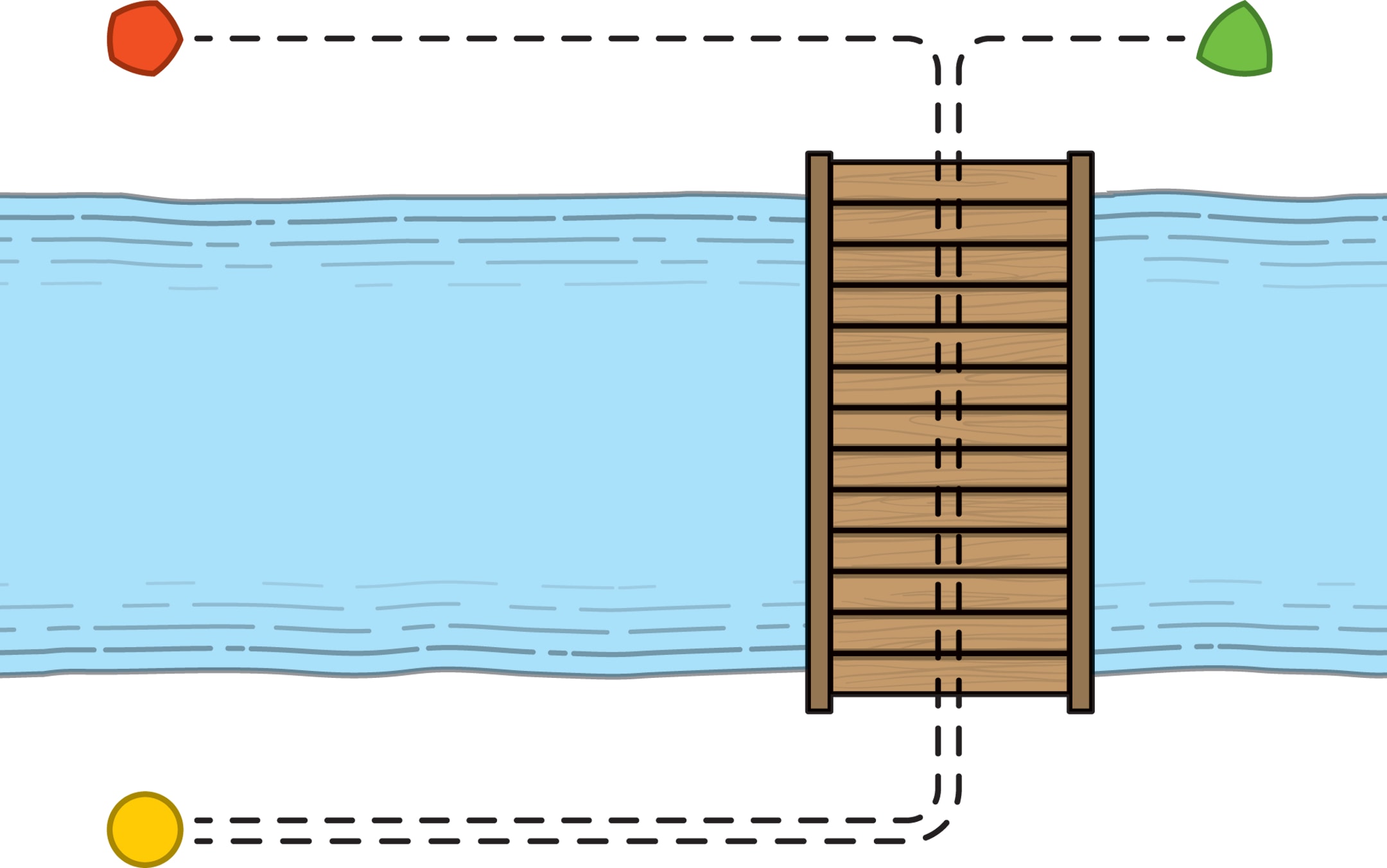
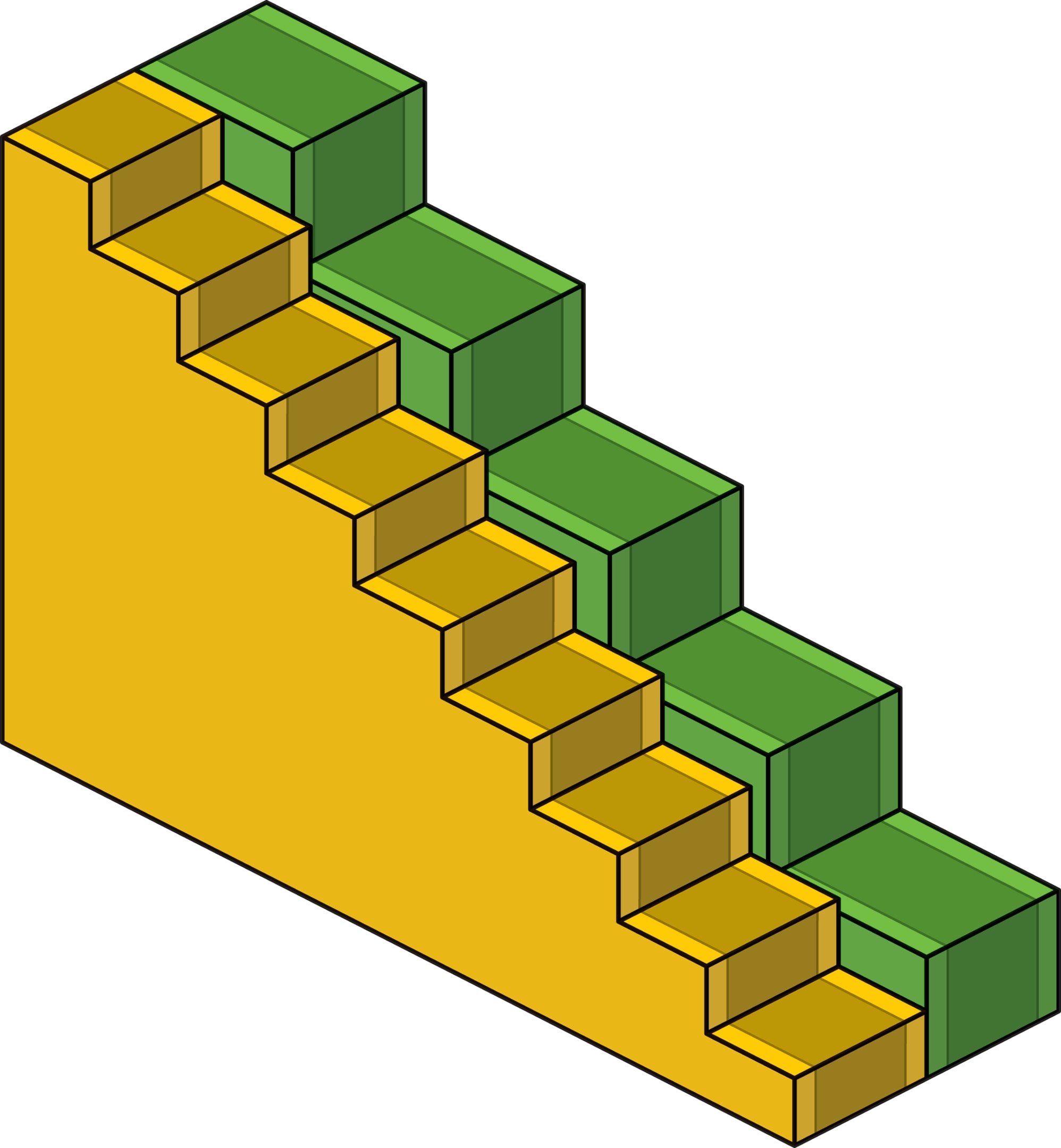
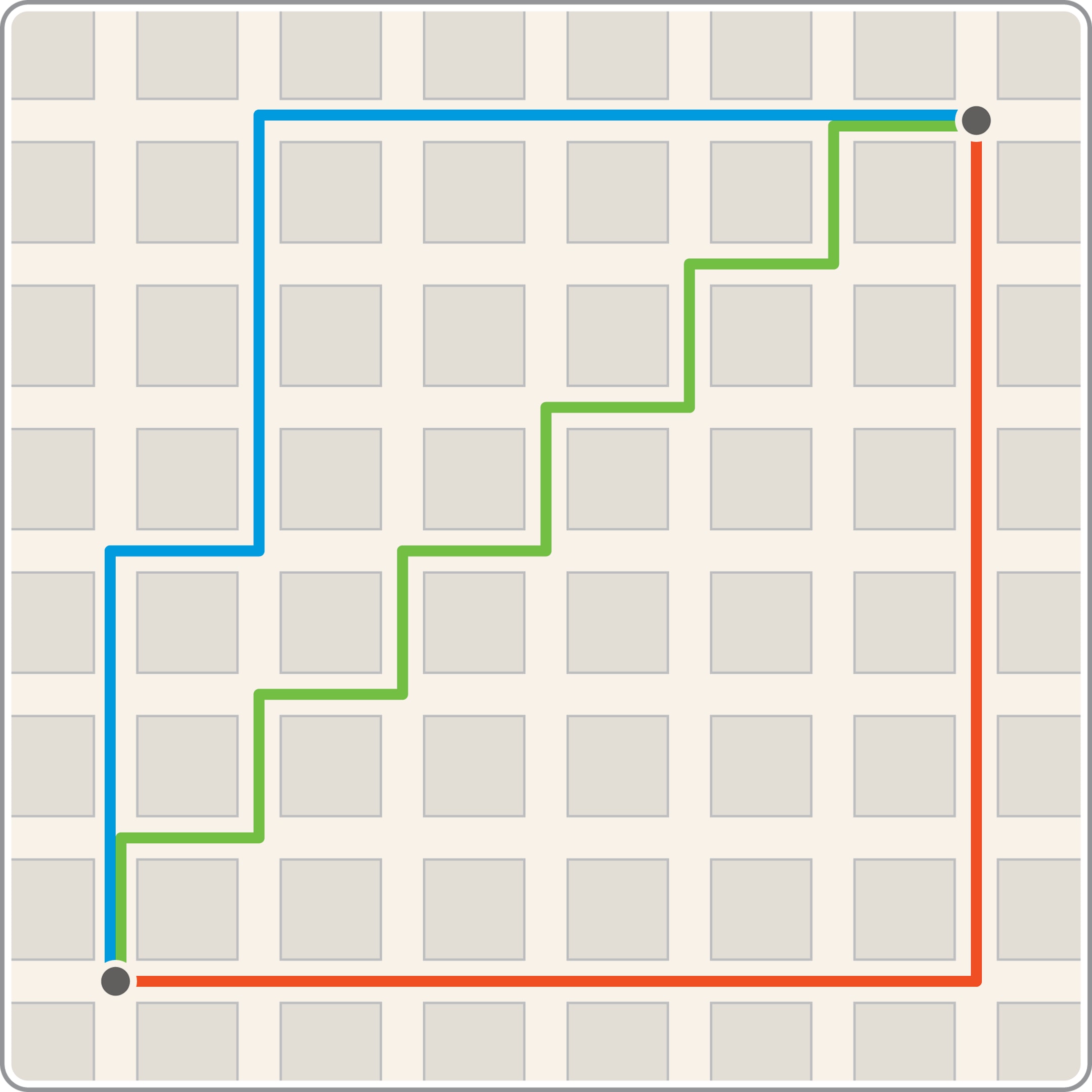
«Расстояние городских кварталов» можно встретить и внутри домов — от дачных домиков до музеев. Размеры ступеней лестничного марша, соединяющего фиксированные точки на площадках, можно выбрать разными (строится «ступенчатая гипотенуза» прямоугольного треугольника). Но длина ковровой дорожки, закреплённой на ступенях лестницы, будет одинаковой независимо от размеров ступенек: сумма длин вертикальных участков ковра равна длине вертикального катета (расстояние по вертикали между площадками), горизонтальных — горизонтального. Это иллюстрация неоднозначного выбора кратчайшего пути в манхэттенской метрике, а ещё — классическая задача для детей.
Шрейдер Ю. А. Что такое расстояние?. — М.: ГИФМЛ, 1963. — (Популярные лекции по математике; Вып. 38).
Скворцов В. А. Примеры метрических пространств. — М.: МЦНМО, 2002. — (Библиотека «Математическое просвещение»; Вып. 16).