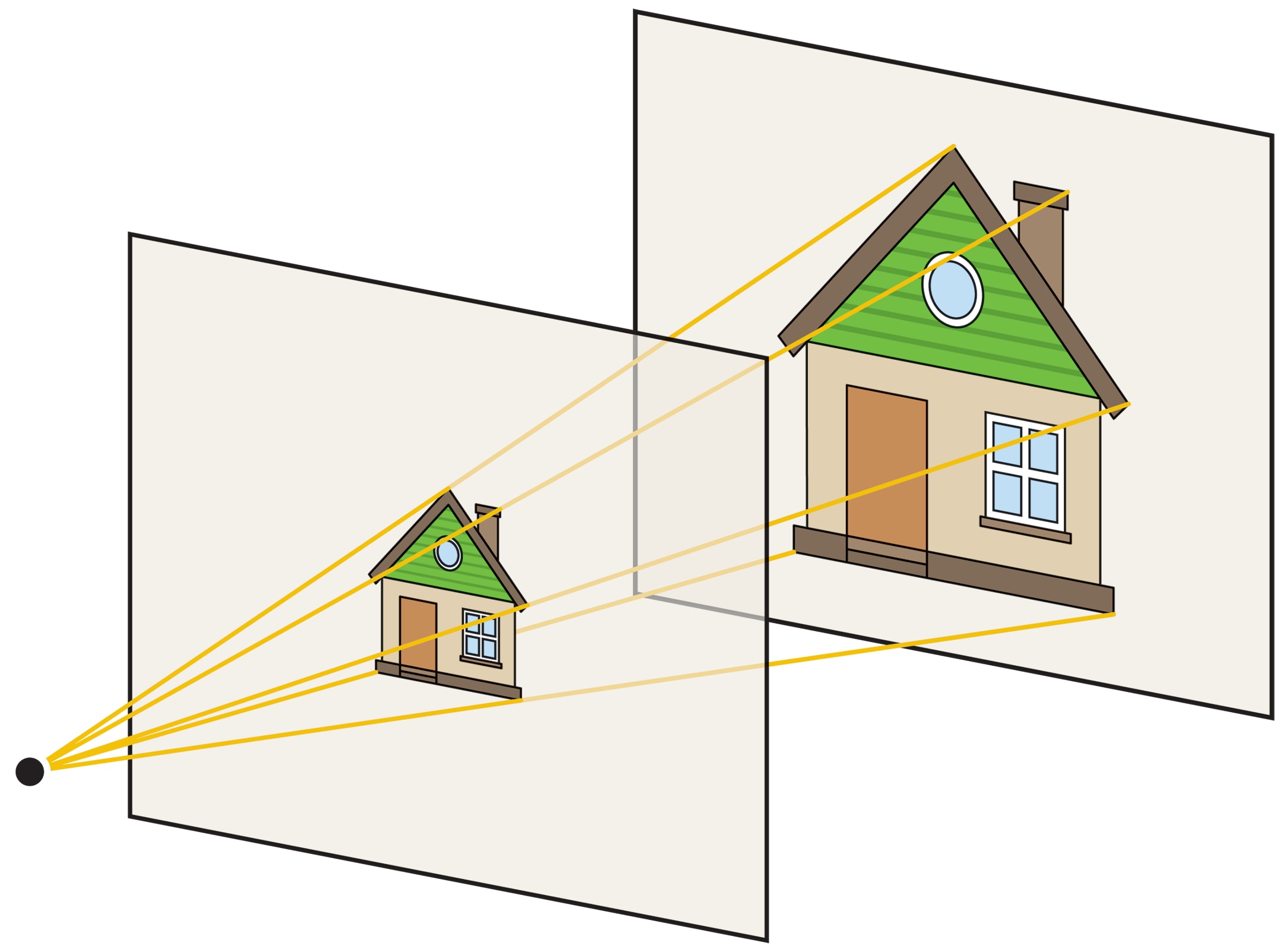
Когда мы смотрим фильм на гигантском экране или разглядываем небольшие фотографии в семейном альбоме, то, независимо от размеров изображения, «правильно» воспринимаем и оцениваем картинку. Так происходит потому, что во всех «копиях» одинаковые пропорции: совпадают и отношения размеров всех объектов, и отношения расстояний между ними.
А какие геометрические инструменты обеспечивают такую «правильность» копирования? Ключевое словосочетание — «преобразование подобия», понятие, изучаемое в школьном курсе геометрии.
При таком преобразовании плоскости (или пространства) расстояния между точками изменяются в одно и то же число раз: если точки $A$ и $B$ переходят в $A_1$ и $B_1$, то $A_1B_1=kAB$, где $k$ — числовая характеристика преобразования, её называют коэффициентом подобия.
Наглядный пример преобразования подобия — гомотетия (соединены древнегреческие слова «одинаковый» и «расположенный»): фиксируются центр $O$ и коэффициент $k>0$, точка $A$ переходит в такую точку $A_1$ на луче $OA$, что $OA_1=k OA$. По сути, всякое преобразование подобия сводится к гомотетии: можно доказать, что преобразование подобия — результат последовательного выполнения гомотетии и движения.
Замечательной чертой преобразования подобия является сохранение важных геометрических свойств. Например, прямые линии переводятся в прямые, сохраняются углы между прямыми.
То, что эти утверждения справедливы в случае движения, очевидно, для гомотетии они выводятся из свойств подобных треугольников. А упомянутая теорема о структуре произвольного преобразования подобия «объясняет», почему они верны и в общем случае.
Cвойства подобия делают исходную картинку и масштабированную копию равноправными изображениями. Сохранение углов, пропорций, характера линий — всё соединяется в сознании зрителя в итоговом решении: это «одинаковые» изображения, портреты одного оригинала, и единственное, что их отличает, — размеры.
Удивительно, что богатый набор полезных свойств преобразования подобия выводится из лаконичного и простого по формулировке определения: все расстояния изменяются в одно и то же число раз.
Определение преобразования гомотетии с центром $O$ и коэффициентом гомотетии $k>0$: точка $A$ переходит в такую точку $A_1$ на луче $OA$, что $OA_1=kOA$. Можно определить гомотетию и при отрицательном значении $k$.
Преобразование гомотетии с центром $O$ и коэффициентом $k=-1$ — это центральная симметрия: точка $A$ переходит в такую точку $A_1$, что $O$ — середина отрезка $AA_1$. При произвольном отрицательном $k$ гомотетия с центром $O$ определяется как композиция гомотетии с положительным коэффициентом $|k|$ и центральной симметрии с центром $O$.
Преобразования подобия можно применять не только к плоским изображениям, но и к трёхмерным объектам. Пример из литературной классики: у Джонатана Свифта попавший в Лилипутию Гулливер обнаруживает, что очутился в мире, в котором все размеры (рост жителей, высота деревьев и домов) в 12 раз меньше привычных, но пропорции те же.