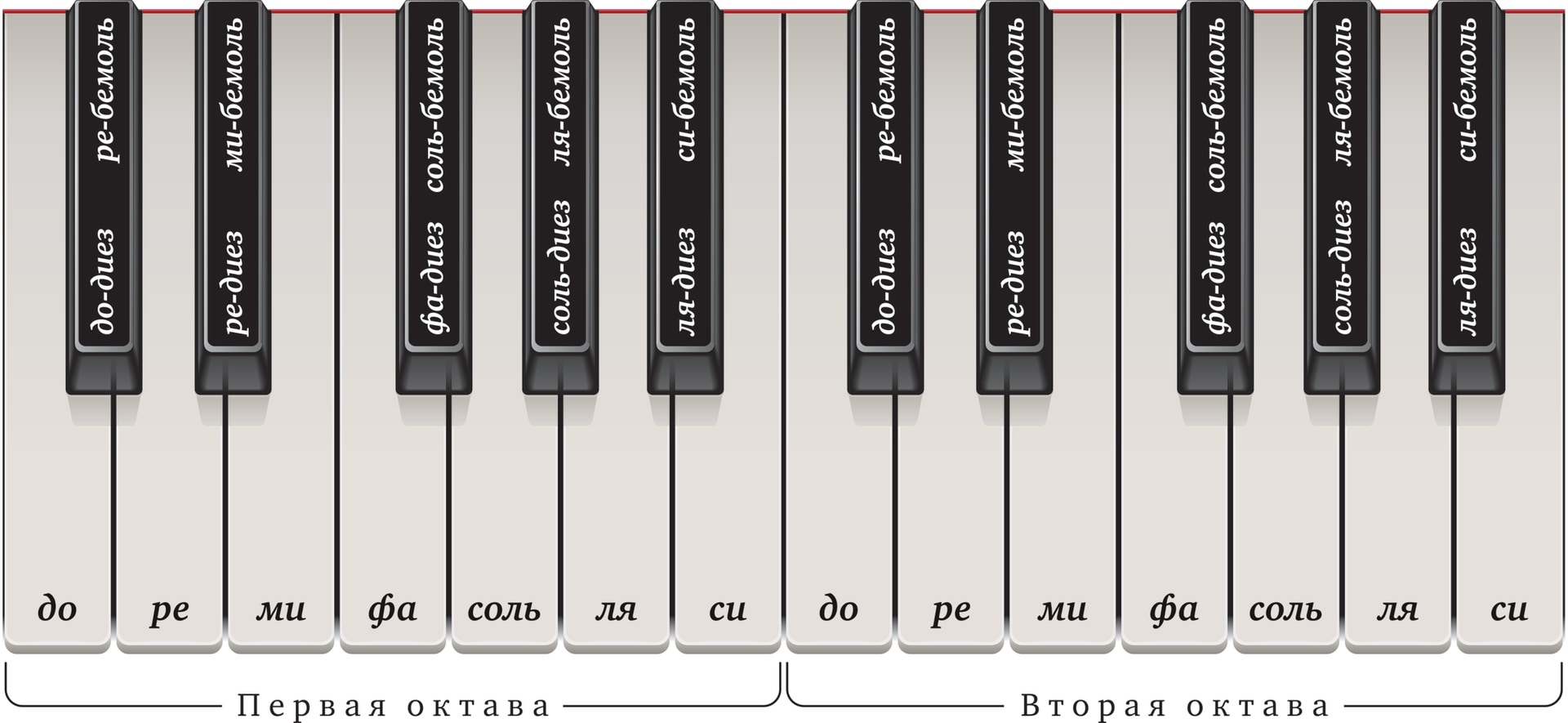
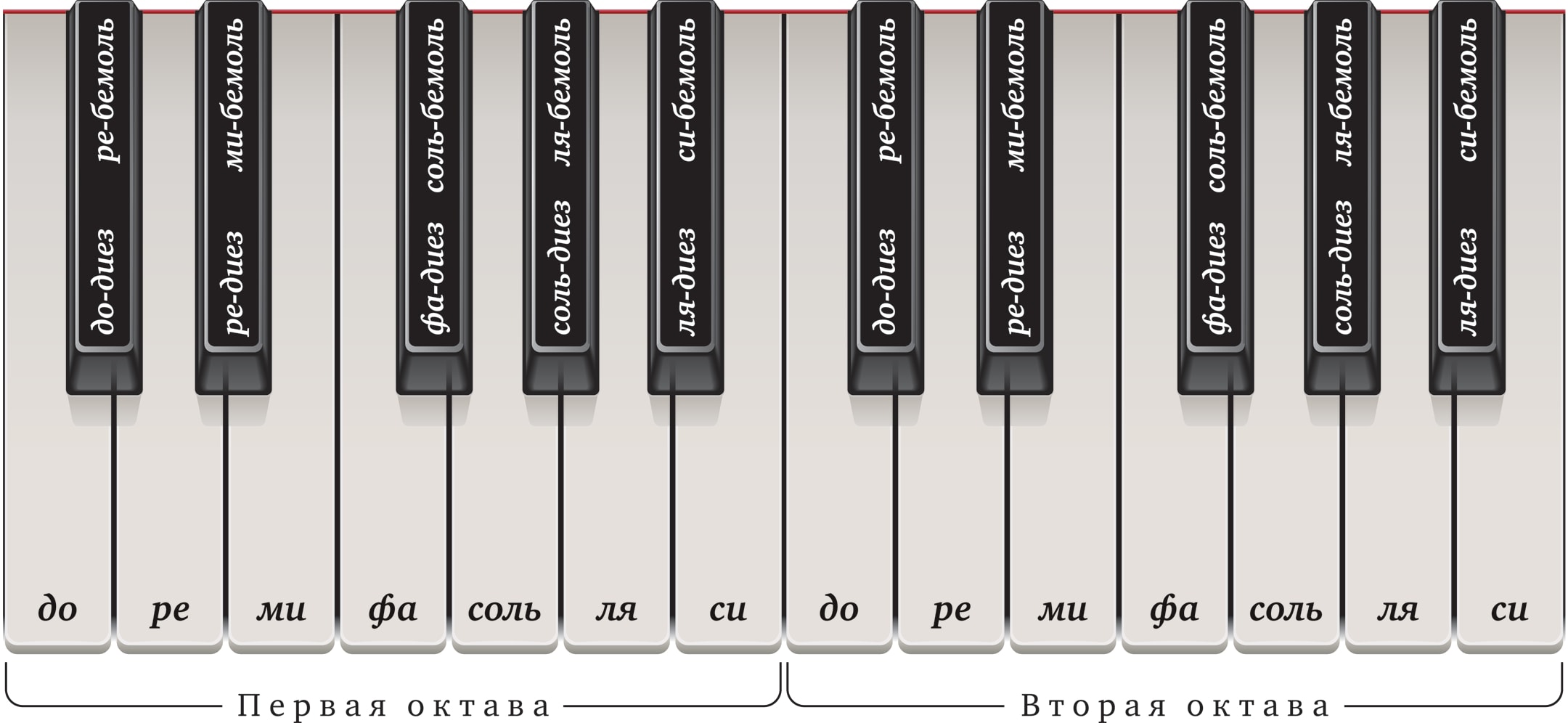
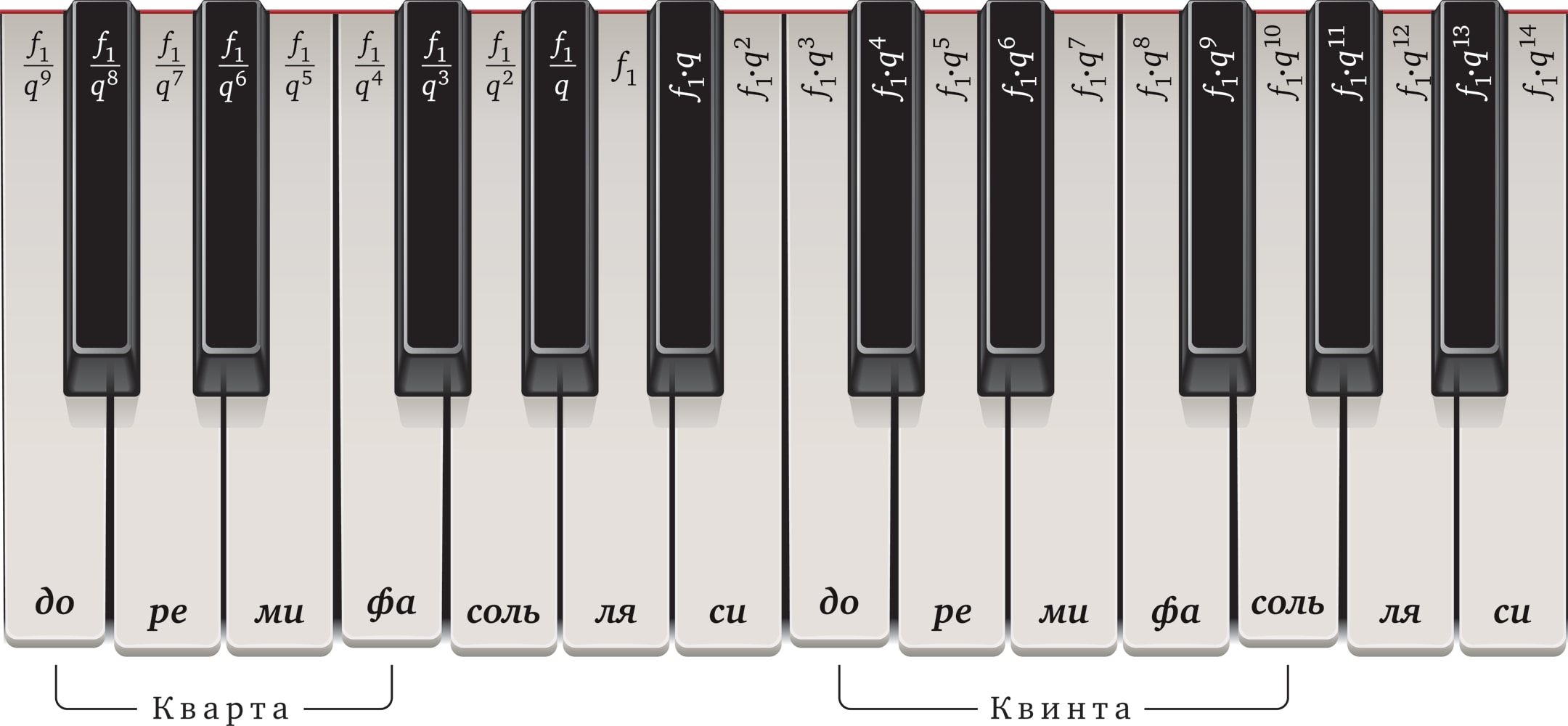
Музыкальный строй — это система сопоставления нот (знаков, обозначений) и звуковых частот. Периодом музыкального строя является октава — интервал между нотами, частоты которых отличаются в два раза. Традиционно октава состоит из 12 ступеней. Например, на клавиатуре рояля она представлена семью основными (белыми) клавишами и пятью дополнительными (чёрными).
Применяемый в наши дни музыкальный строй допускает прозрачное и изящное математическое описание.
Появление в первой половине XVIII века сочинения Иоганна Себастьяна Баха «Хорошо темперированный клавир» канонизировало равномерно темперированный строй — музыкальный строй, в котором отношение звуковых частот соседних нот является величиной фиксированной. Будем обозначать это отношение через $q$ (большей частоты к меньшей, $q>1$).
Таблица частот нот равномерно темперированного строя может быть представлена в виде двусторонней последовательности, в которой соединены две геометрические прогрессии.
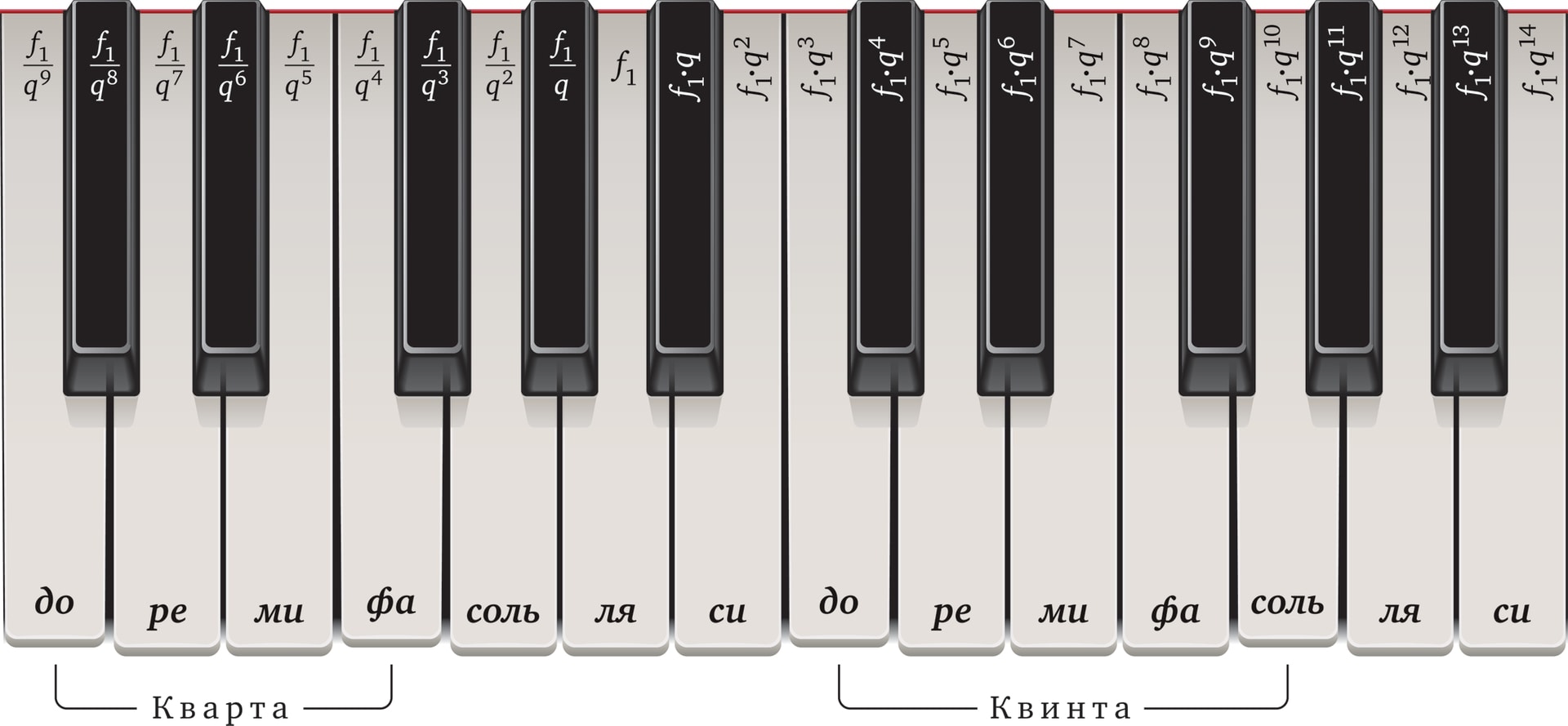
В качестве точки отсчёта берётся нота «ля» первой октавы, пусть $f_1$ — её частота. Правая ветвь последовательности — возрастающая геометрическая прогрессия $f_1$, $f_1q$, $f_1q^2$, …, её знаменатель равен $q$. Левая ветвь — убывающая геометрическая прогрессия $f_1$, $\frac{f_1}{q}$, $\frac{f_1}{q^2}$, … со знаменателем $\frac{1}{q}$.
Зная на сколько выбранная нота отстоит от «точки отсчёта», можно выписать формулу, связывающую частоты этих двух нот. Например, для правой ветви элемент геометрической прогрессии с номером $n$ вычисляется по формуле $f_n=f_1\cdot q^{n-1}$.
По определению октавы $f_{n+12}=2\cdot f_n$. С другой стороны, для элементов геометрической прогрессии $f_{n+12}=f_n\cdot q^{12}$. Значит, $ f_n\cdot q^{12}=2\cdot f_n $, откуда $q^{12}=2$. Следовательно, для октавы из 12 ступеней равномерно темперированного строя фундаментальной характеристикой, мультипликативным (т. е. по умножению) шагом, определяющим «равномерность» движения по последовательности частот, является число $ q=\sqrt[12]{2}=1{,}059463… $
Фиксация значения частоты ноты «ля» (например, по камертону) полностью определяет частоты всех нот равномерно темперированного строя. В наши дни каноническим вариантом является значение $f_1=440$ Гц.
В восприятии человеком мелодии отношение частот звучащих (последовательно или одновременно) нот важнее, чем их абсолютные величины. Именно это обстоятельство привело к осознанной необходимости выбора частот музыкального строя по «мультипликативному» принципу.
Постоянство «мультипликативного» шага у равномерно темперированного строя обусловило его главное преимущество перед историческими предшественниками — возможность сдвигать музыкальные мелодии на произвольное число ступеней. При сдвиге фрагмента отношение частот соседних нот остаётся неизменным, а следовательно, сохраняется и мелодический рисунок.
К построению музыкального строя как последовательности частот можно подойти аксиоматически, указав набор желательных свойств:
1) вместе с каждой частотой $f$ в строй входят частоты $2f$ и $\frac12 f$ (от каждой ноты можно построить октаву и вверх, и вниз);
2) любую мелодию можно сдвигать на произвольное число ступеней без искажений.
Оказывается, сформулированная задача имеет единственное решение — равномерно темперированный строй. Математически это означает, что набор частот $\{f_n\}$ является геометрической прогрессией.
Равномерно темперированный строй совершенен не во всех отношениях. Один из самых заметных недостатков — отсутствие всех чистых интервалов, кроме октавы — периода («Чистые интервалы»). Например, здесь нет ни чистой квинты (двух звуков, отношение частот которых равно 3/2), ни чистой кварты (4/3).
Квинту образуют ноты «до» и «соль», отношение частот равно $q^7$ (в силу равномерности строя интервал можно строить от любой ноты). Напомним, что в октаве за 12 шагов частота повышается в два раза, $q^{12}=2$, т. е. знаменатель прогрессии $q=\sqrt[12]{2}=2^{1/12}$. Поэтому квинта не является чистой: $2^{7/12}\ne\frac{3}{2}$. Аналогично, кварта в равномерно темперированном строе не является чистой, $2^{5/12}\ne\frac{4}{3}$. В обоих случаях всё сводится к тому, что $2^m\ne 3^n$ ни при каких натуральных $m$ и $n$.
Деление октавы именно на 12 ступеней (шагов) оптимально с точки зрения приближения чистых интервалов (см. «Чистые интервалы»). Это можно вывести, используя цепные дроби. В статье «Високосное летосчисление») цепные дроби показали свою эффективность в задаче нахождения наилучшего календаря.
Для чистой квинты разложение в цепную дробь имеет вид $$ \log_2\frac{3}{2}= \frac1{1+\frac1{1+\frac1{2+\frac1{2+\frac1{3+…\vphantom{\frac12} }}}}}. $$
(Выбор числа 2 как основания логарифма связан с отношением частот двух звуков, образующих октаву.)
Первые подходящие дроби этого разложения: $$ \displaylines{ 0,\quad \frac{1}{1}=1,\quad \frac1{1+\frac1{1}}=\frac{1}{2},\quad \frac1{1+\frac1{1+\frac1{2}}}=\frac{3}{5},\cr \frac1{1+\frac1{1+\frac1{2+\frac1{2}}}}=\frac{7}{12},\quad \frac1{1+\frac1{1+\frac1{2+\frac1{2+\frac1{3}}}}}=\frac{24}{41}.\cr}$$
Среди приведённых подходящих дробей есть и канонический вариант: выбирается октава из 12 нот, «расстояние» между нотами, образующими квинту, — 7 шагов. Другие приближения проигрывают: пара «5 нот, 3 шага» — грубая, неточная; делить октаву на 41 шаг — неудобно практически.
Значение квинты, подсказанной цепными дробями, близко к чистой квинте: $q^7=(\sqrt[12]{2})^7≈ 1{,}4983≈ \frac{3}{2}$. Чистая кварта $\frac43=1{,}33333…$ также хорошо приближается значением кварты $q^5=(\sqrt[12]{2})^5≈ 1{,}3348$.
Сколько в году длинных месяцев (длиной 31 день)? Как запомнить чередование длинных и коротких месяцев? На оба вопроса можно ответить, взглянув на костяшки рук.
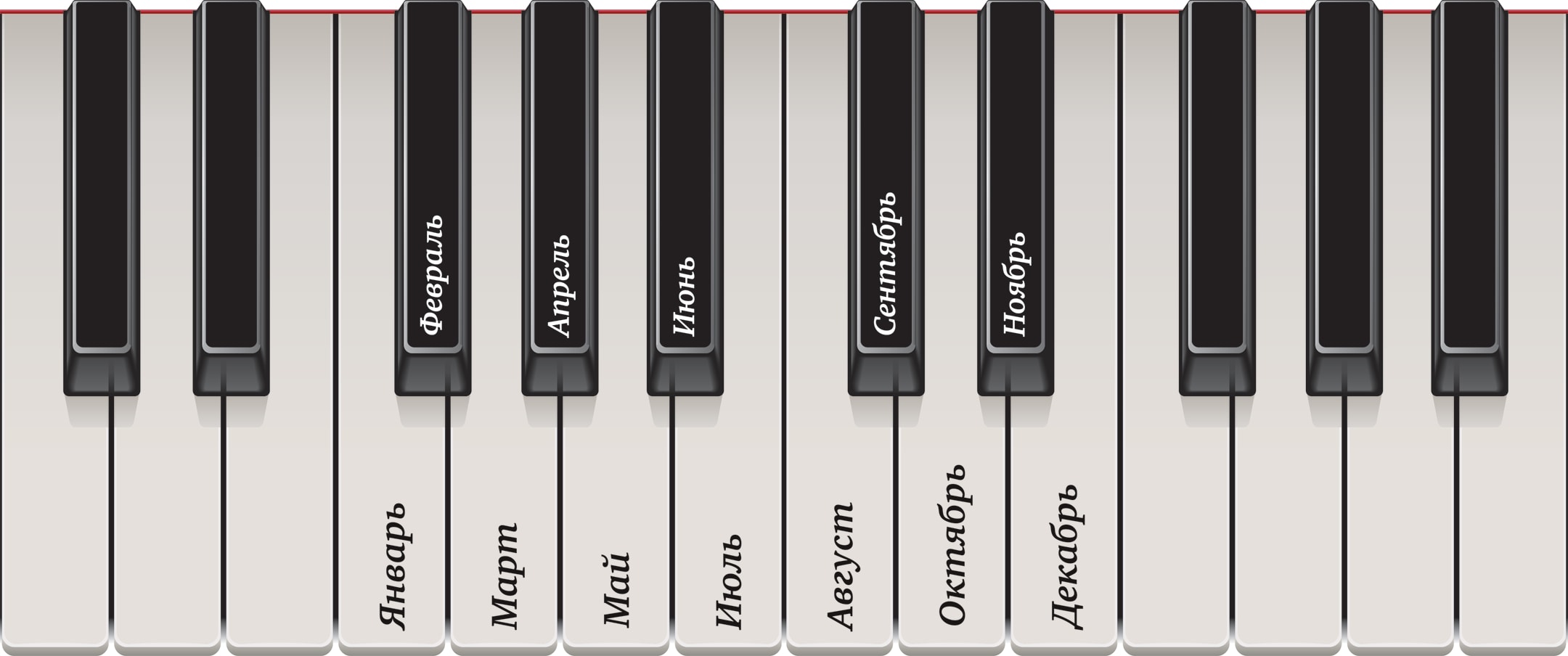
Неожиданным является представление месяцев как белых и чёрных клавиш пианино или рояля (Концевич М. Равномерные расположения
Совпадение чередований длинных и коротких месяцев, длинных и коротких клавиш — неслучайно. Октава из 12 нот — период музыкального строя, год, состоящий из 12 месяцев, — тоже период. В обоих случаях возникает «окружность», на которой белые и чёрные клавиши, длинные и короткие месяцы распределены правильно, равномерно. Если определить равномерность разумно-математически, то оказывается, что при любых натуральных $n$ и $k$ равномерное распределение на окружности $n$ белых и $k$ чёрных точек — единственное (с точностью до поворота окружности). В наших примерах (октава и год) $n=7$ и $k=5$.
Штейнгауз Г. Математический калейдоскоп. — М.—Л.: Гостехиздат, 1949. — [Параграфы «Решётка целых чисел» и «Темперированная гамма рояля»].
Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. — М.: Физматлит, 1963. — (Популярные лекции по математике; Вып. 37).
Варга Б., Димень Ю., Лопариц Э. Язык, музыка, математика. — М.: Мир, 1981.
Волошинов А. В. Математика и искусство. — 2‐е изд. — М.: Просвещение, 2000.
Джинс Дж. Наука и музыка. — М.: Институт компьютерных исследований, 2011.
Способин И. В. Элементарная теория музыки. — М.: Музгиз, 1963.
Loy G. Musimathics: the mathematical foundations of music. — V. 1, 2. — MIT Press, 2006, 2007.