Пчелиные соты издавна вызывают у человека восхищение симметрией и красотой своей архитектуры. Удивительно, но оптимальность создаваемых пчёлами конструкций математически обосновать удалось только на протяжении последнего столетия.
На самом деле, пчёлы-строители из вырабатываемого ими воска сооружают ячейки в виде цилиндров (а не шестиугольных призм). Пчела движется от основания ячейки и, вращаясь, лепит вокруг себя стенки цилиндра. Диаметры ячеек почти совпадают, поскольку рабочие пчёлы примерно одного размера.
Основания ячеек пчёлы закладывают в виде гексагональной укладки кругов, которая на плоскости является плотнейшей. Пчёлы так делают веками, а математики доказали оптимальность данной укладки только к середине XX века. Упомянем, что аналогичная задача для шаров в трёхмерном пространстве (гипотеза Кеплера) была решена лишь в конце XX века, а в XXI веке — ещё и в пространствах размерностей 8 и 24.
Но хотя укладка цилиндров и наиплотнейшая, между ними остаются зазоры. Этот недостаток исчезает уже без участия пчёл: пока воск пластичен, под действием сил поверхностного натяжения (как в мыльных плёнках) стенки ячеек принимают форму примыкающих друг к другу шестиугольных призм.
Воск для пчёл — дорогой материал (в сравнении с мёдом), поэтому, строя соты, надо выбрать такую архитектуру, чтобы расход воска был минимальным при разбиении данного большого объёма на одинаковые ячейки.
Оказывается, оптимальность укладки кругов на плоскости «наследуется» шестиугольниками, в которые они превратились: получается самый экономичный вариант по расходу воска.
Математическая постановка задачи такова: надо найти разбиение большой плоской области на элементы малой фиксированной площади (размер пчелы), у которого суммарный периметр границ будет наименьшим. Без дополнительных условий (например, что элементы — выпуклые) задача оказалась сложной. Только в начале XXI века задача была решена в общей постановке: разбиение на правильные шестиугольники оказалось наилучшим.
Но если считать, что элементы разбиения — одинаковые правильные многоугольники, то объяснить преимущество шестиугольников несложно. Ясно, что плоскость можно замостить правильными треугольниками, квадратами, правильными шестиугольниками. Оказывается, других вариантов нет.
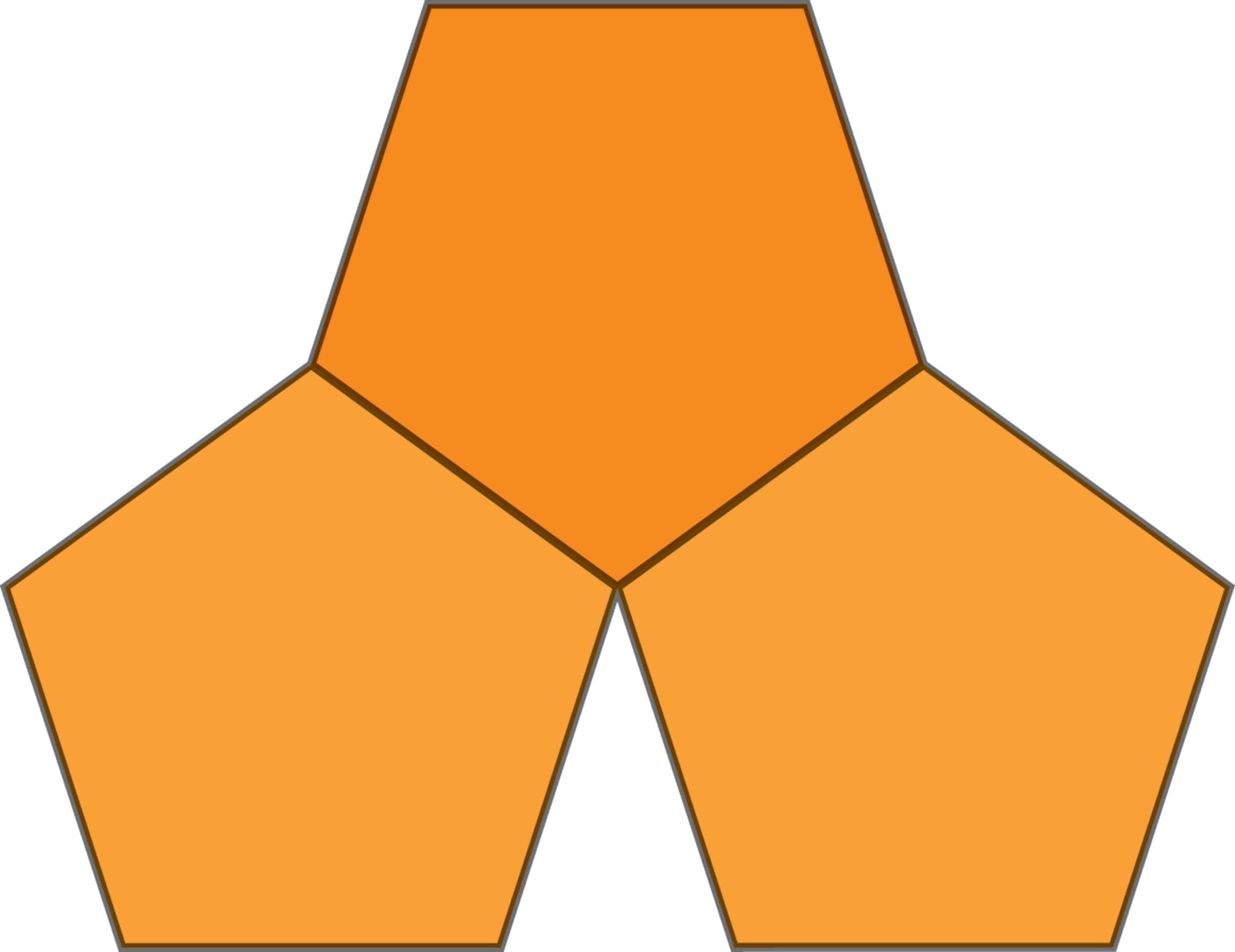
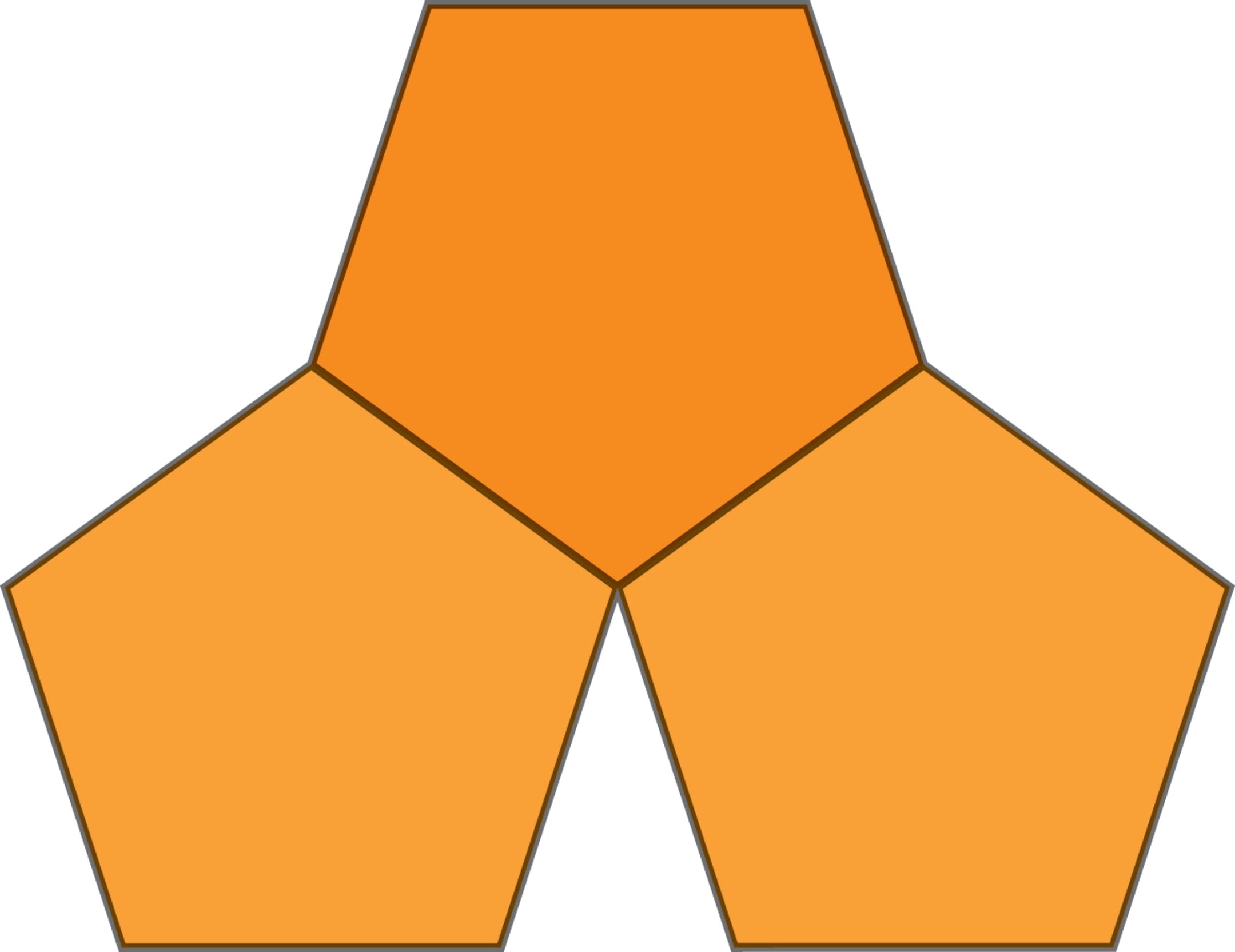
Например, если к двум смежным сторонам правильного пятиугольника приложить такие же пятиугольники, то около общей вершины «незаполненным» останется угол, который, очевидно, замостить не удастся. По аналогичным соображениям не удастся замостить плоскость и правильными $n$‐угольниками, если $n\ge 7$: у каждого угол при вершине больше, чем $120°$ (угол в правильном шестиугольнике), «незаполненный» внешний угол в общей вершине двух $n$‐угольников слишком мал — третий уже не помещается.
Осталось сравнить три перечисленных разбиения по величине суммарного периметра границ. Несложные вычисления показывают, что в цепочке элементов равной площади «треугольник — квадрат — шестиугольник» их периметры монотонно уменьшаются. Чтобы найти суммарный периметр границ разбиения, надо сложить периметры элементов и разделить сумму на 2, так как во «внутренней» части отрезки границ будут сторонами сразу двух прилегающих многоугольников. Значит, наилучшим является разбиение на правильные шестиугольники.
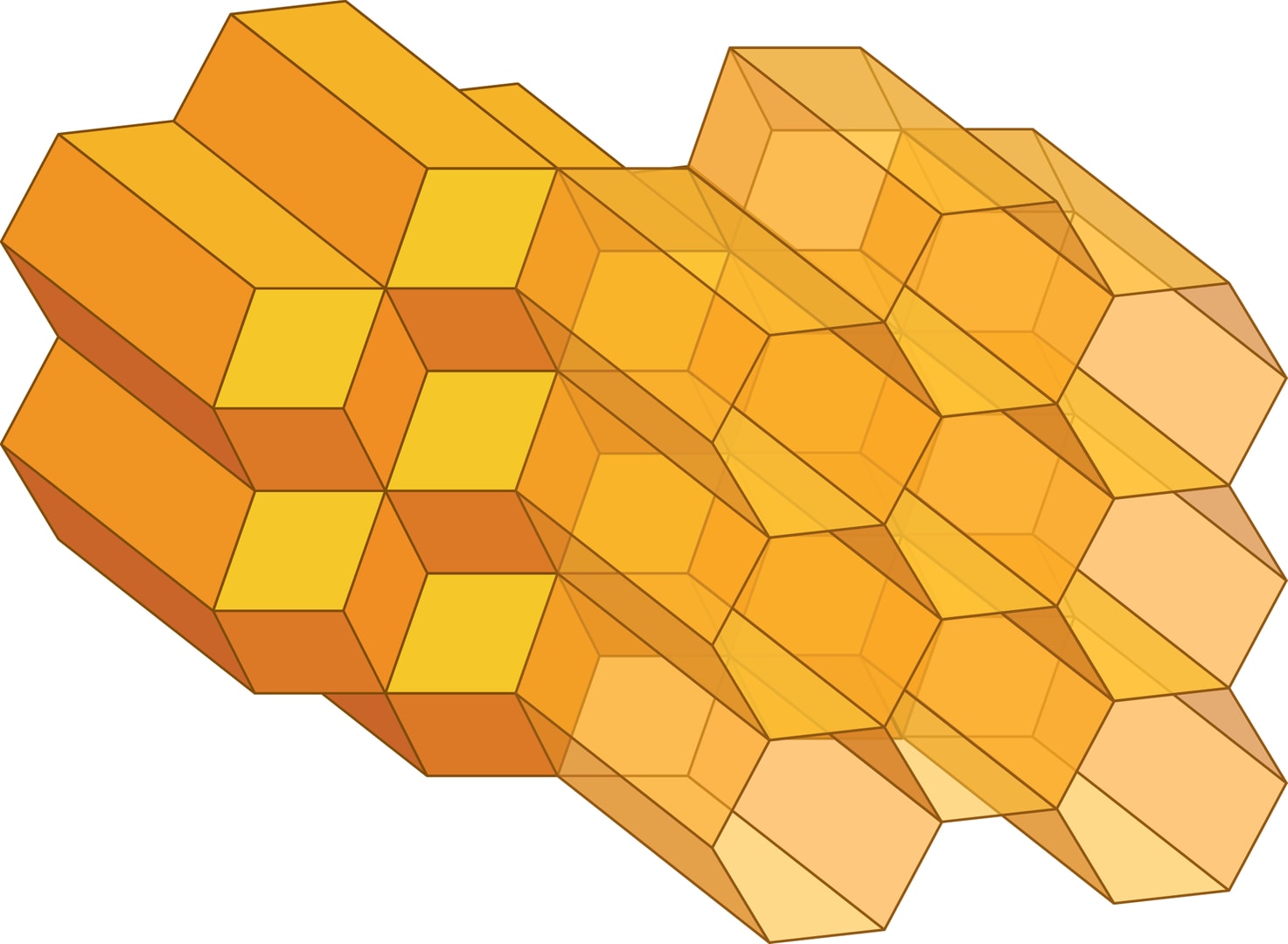
Следовательно, и гексагонально уложенные шестиугольные призмы-ячейки образуют слой, в сооружении которого использовано минимальное количество воска. У всех ячеек слоя общее плоское дно, а входы с одной стороны. В природе пчёлы сооружают сразу два слоя с общим днищем. Сдвиг слоёв относительно друг друга превращает плоское дно каждой призмы в трёхгранный выступ, объём ячеек увеличивается, а два слоя оказываются накрепко состыкованными.
Архитектуру пчелиного таунхауса отличают два важных свойства: оптимальность по затратам воска и высокая прочность.
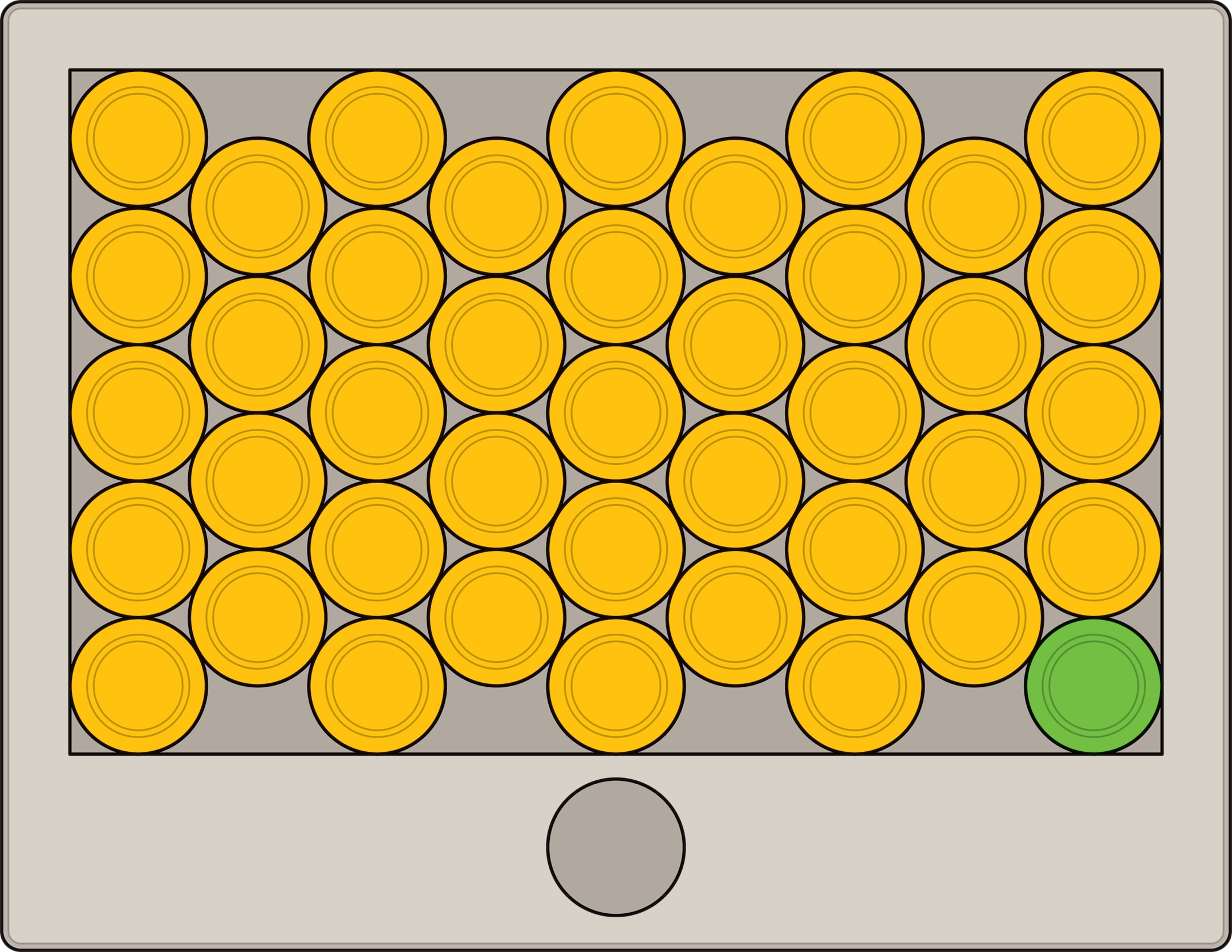
Гексагональная упаковка кругов на плоскости является плотнейшей. Это «знают» пчёлы, это знание можно воплотить и в головоломке, задание которой кажется невыполнимым.
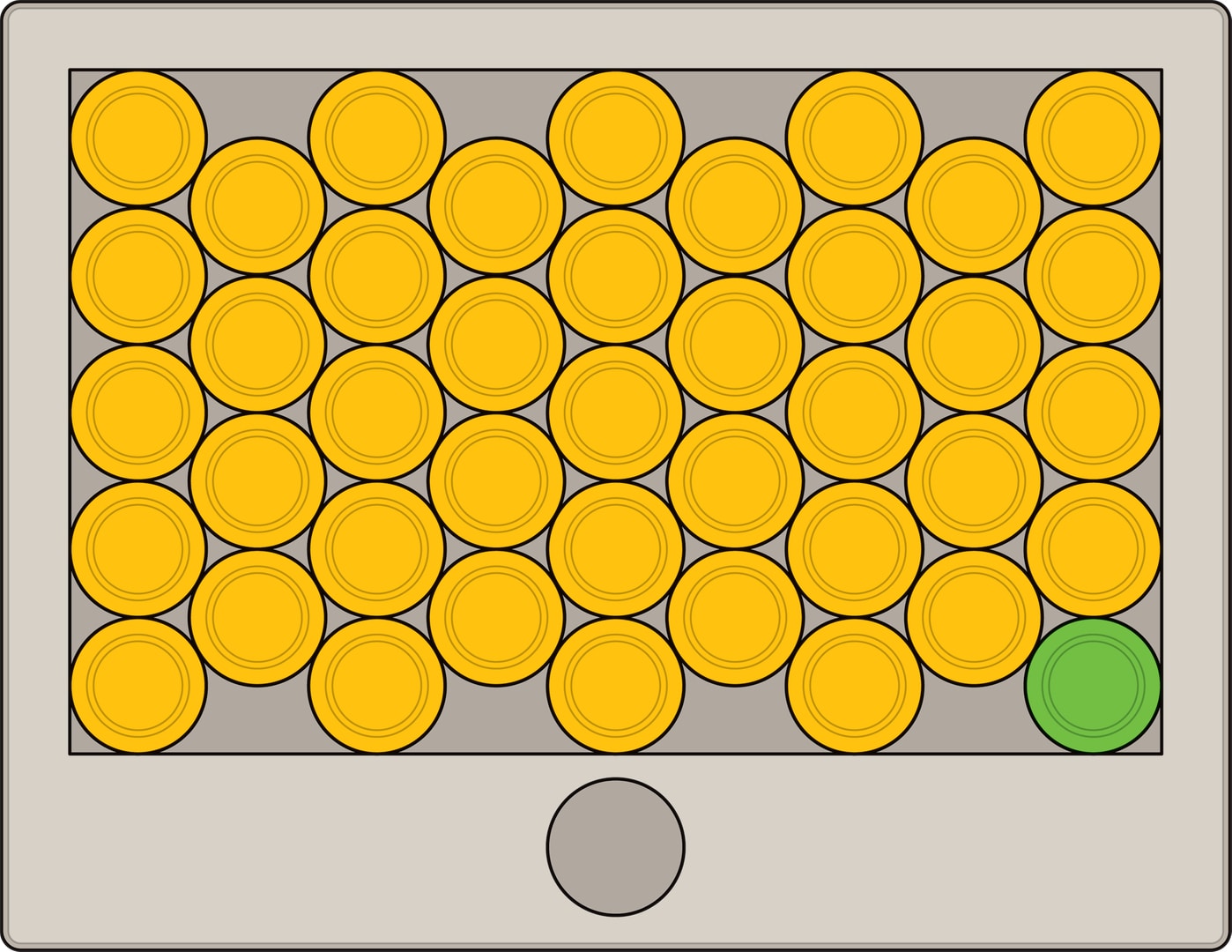
На прямоугольном поле, ограниченном невысокой рамкой, расположены вплотную друг к другу 40 одинаковых кружков (шайб), их центры образуют квадратную решётку. Оказывается, можно переложить кружки так, чтобы внутри рамки уместился 41 кружок!
Кружки можно вырезать из картона, а можно использовать и готовые варианты — монеты, пуговицы и т. п. Поле и рамку можно изготовить из фанеры, листа пластика, даже из плотного картона. Сначала надо определить размеры поля, соответствующего каре из кружков $5\times 8$, а затем наклеить прямоугольное обрамление, рамку. (Поле $5\times 8$ — наименьшее прямоугольное, в котором возможно провести «уплотнение», разместить ещё один кружок.)