Детские книжки-панорамы с поднимающимися фигурами рыцарей и стенами замков, промопродукция компаний, притягивающая взрослых своей трёхмерной рекламной убедительностью — конструкции, основанные на эффекте Pop Up (= внезапно подняться). Проектирование таких конструкций — по сути, геометрическая задача.
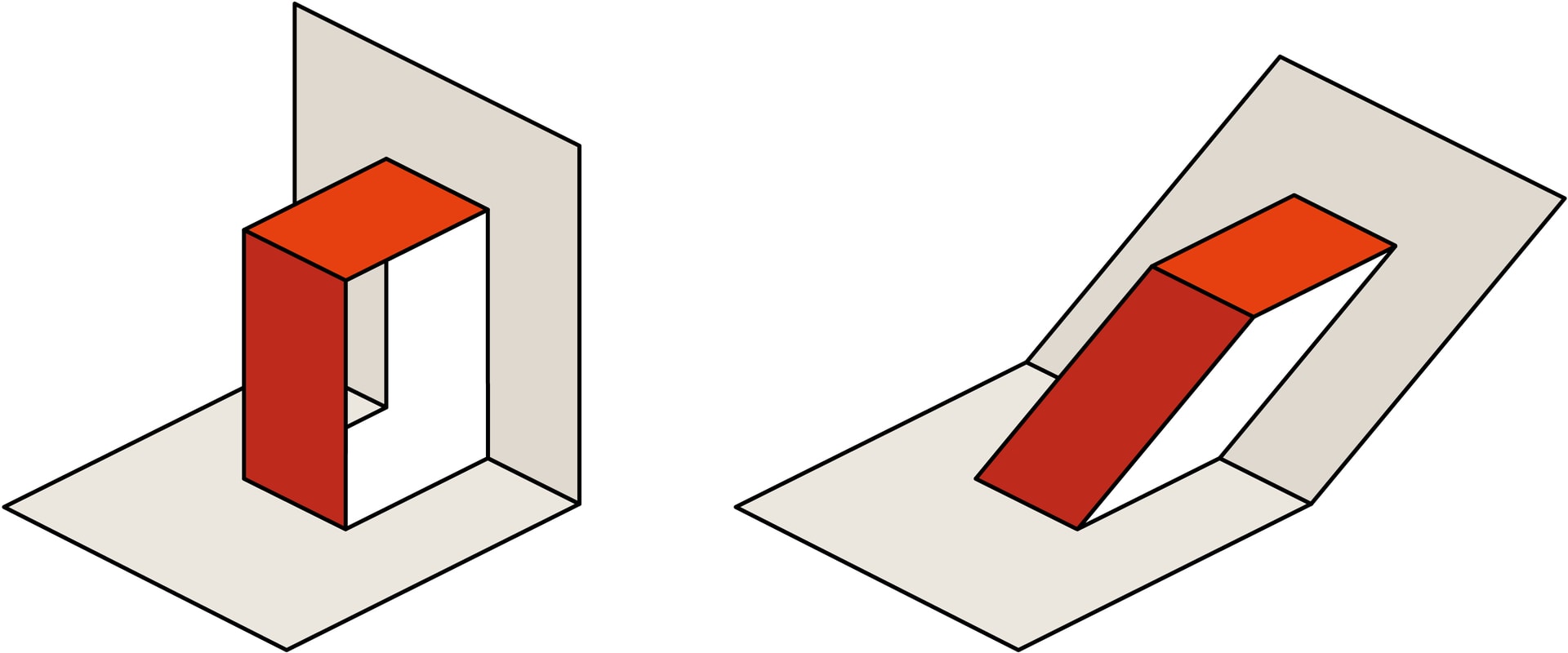
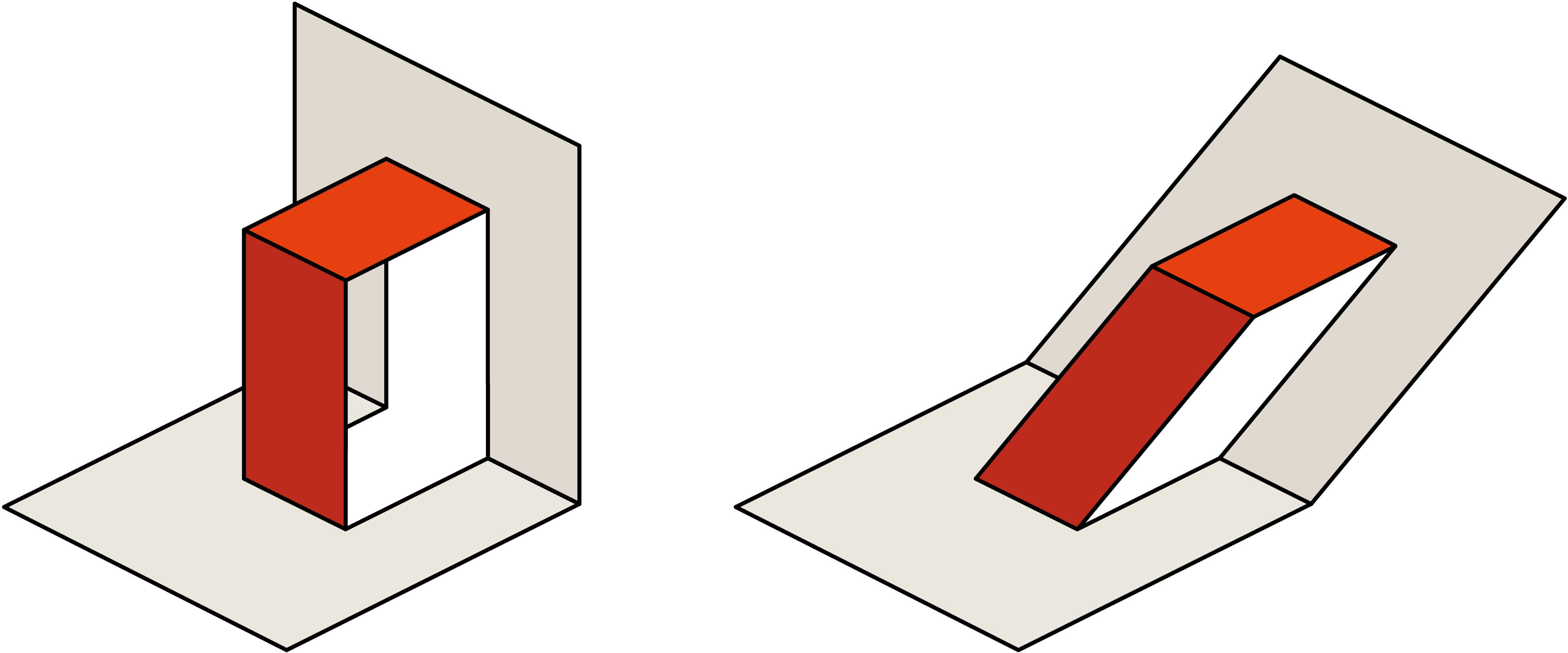
Книжки-панорамы обычно раскрываются полностью, на $180°$. Наиболее популярная основа механизма Pop Up в этом случае — прикреплённая к страницам разворота V‐образная картонная конструкция, по‐английски — V‐fold, а с точки зрения геометрии — двугранный угол.
Для достижения различных эффектов иногда требуется, чтобы грани угла были перпендикулярны развороту, иногда — чтобы грани были наклонены внутрь или наружу конструкции. Определяют эти случаи два плоских угла: $α$ — угол между ребром двугранного угла и линией приклейки, $β$ — угол между сгибом книги и линией приклейки (будем считать, что $β<90°$, т. е. V‐угол обращён ребром к нам).
Чтобы получить действующую конструкцию, соотношения между $α$ и $β$ должны быть следующими.
Грани двугранного угла перпендикулярны развороту: необходимо, чтобы выполнялись условия $α = 90°$, $β < 90°$.
Грани и ребро двугранного угла отклоняются от нас: $α < 90°$, $β < 90°$, $α ≥ β$. При фиксированном $β$ уменьшение $α$ увеличивает наклон ребра («от нас»). В пределе при $α = β$ угол не будет подниматься, будет «лежачим». При фиксированном $α$ уменьшение $β$ уменьшает наклон ребра.
Грани и ребро наклонены к нам: $α > 90°$, $β < 180° - α$. При фиксированном $α$ уменьшение $β$ уменьшает наклон, ребро и грани приближаются к вертикальному положению.
Ещё один важный для конструкций Pop Up механизм — «параллелограмм». Напомним, что у параллелограмма противоположные стороны равны и параллельны. Особенность «параллелограмм»-конструкций — вырубаться они могут из «разворачивающегося» картона, а могут быть и внешними, приклеенными к нему, например, дополнять элементы V‐fold.
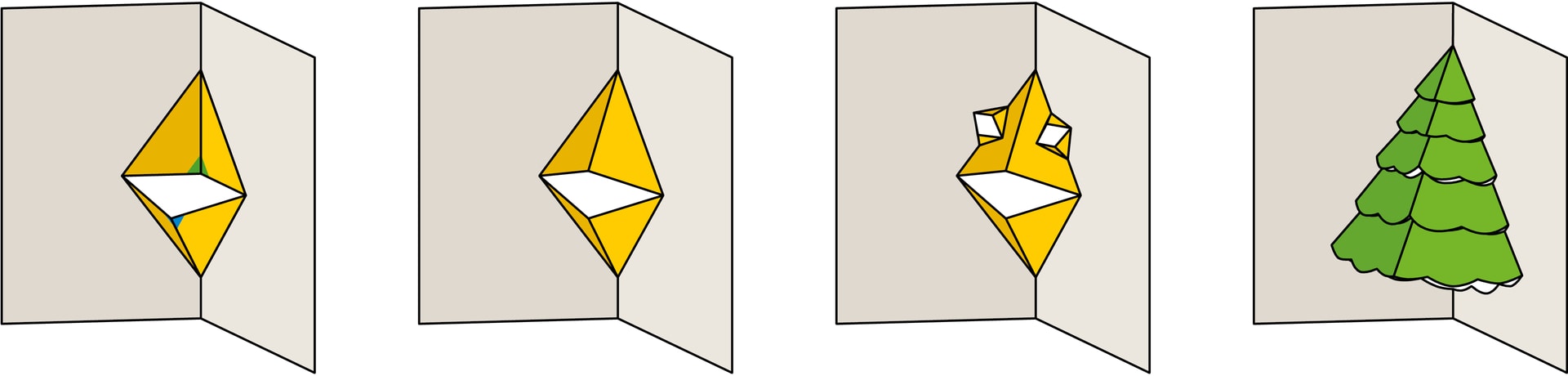
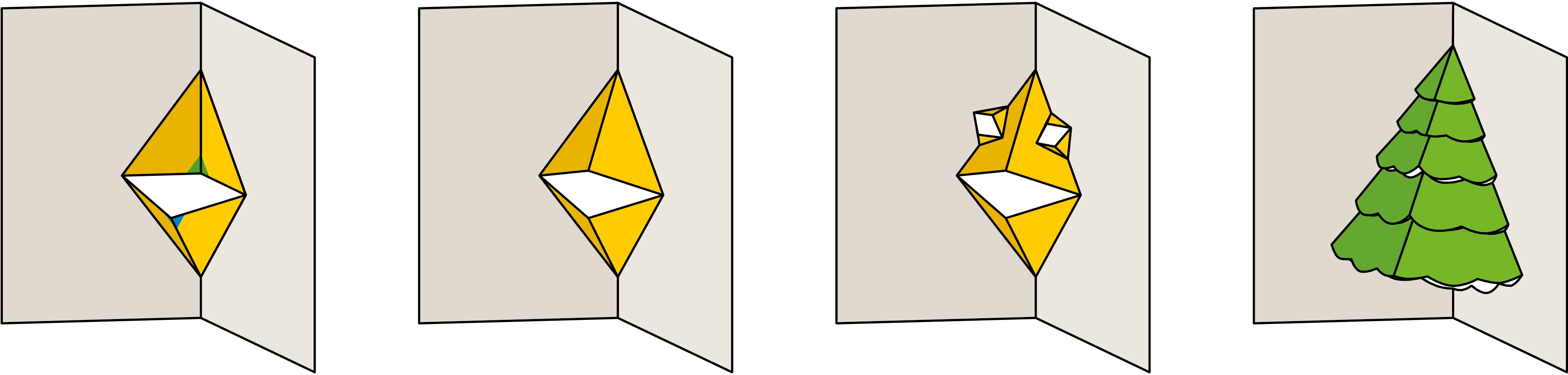
Для открыток, которые раскрываются не полностью на $180°$, а на меньший угол, обычно $90°$, конструкцию Pop Up часто вырубают из картона самой открытки. Простейшая конструкция в данном случае — часть двугранного угла, состоящая из двух треугольников, определяемых своими сторонами (левый рисунок). При фиксированном неполном развороте открытки система квадратных уравнений, определяющая координаты подвижной вершины, имеет ровно два решения, которым соответствуют зелёная и синяя точки.
Типов простейших конструкций немного, но из них, как из «кирпичиков», можно создать весьма затейливые сооружения. Подобно архитектуре, многообразие форм возникает за счёт комбинирования и кирпичиков, и строительных приёмов. Так, можно включить в конструкцию Pop Up несколько однотипных элементов (пример — «ёлочка»), можно использовать цепочку однотипных элементов, в которой последующий элемент вырезается из предыдущего (пример — лесенка, сделанная на основе «параллелограмма»). Можно использовать и сложные композиции простейших элементов.