Каждый раз, когда мы работаем на компьютере или говорим по мобильному телефону, запускаются мощные механизмы обработки, хранения и передачи сигналов. Эти механизмы основаны на достижениях теории функций, оптимизации, теории алгоритмов и ещё десятка областей современной математики. Одни из них родились ещё в позапрошлом веке, другие (и их большинство) — практически вчера. Теория обработки сигналов является одним из наиболее востребованных практикой разделов сегодняшней математики.
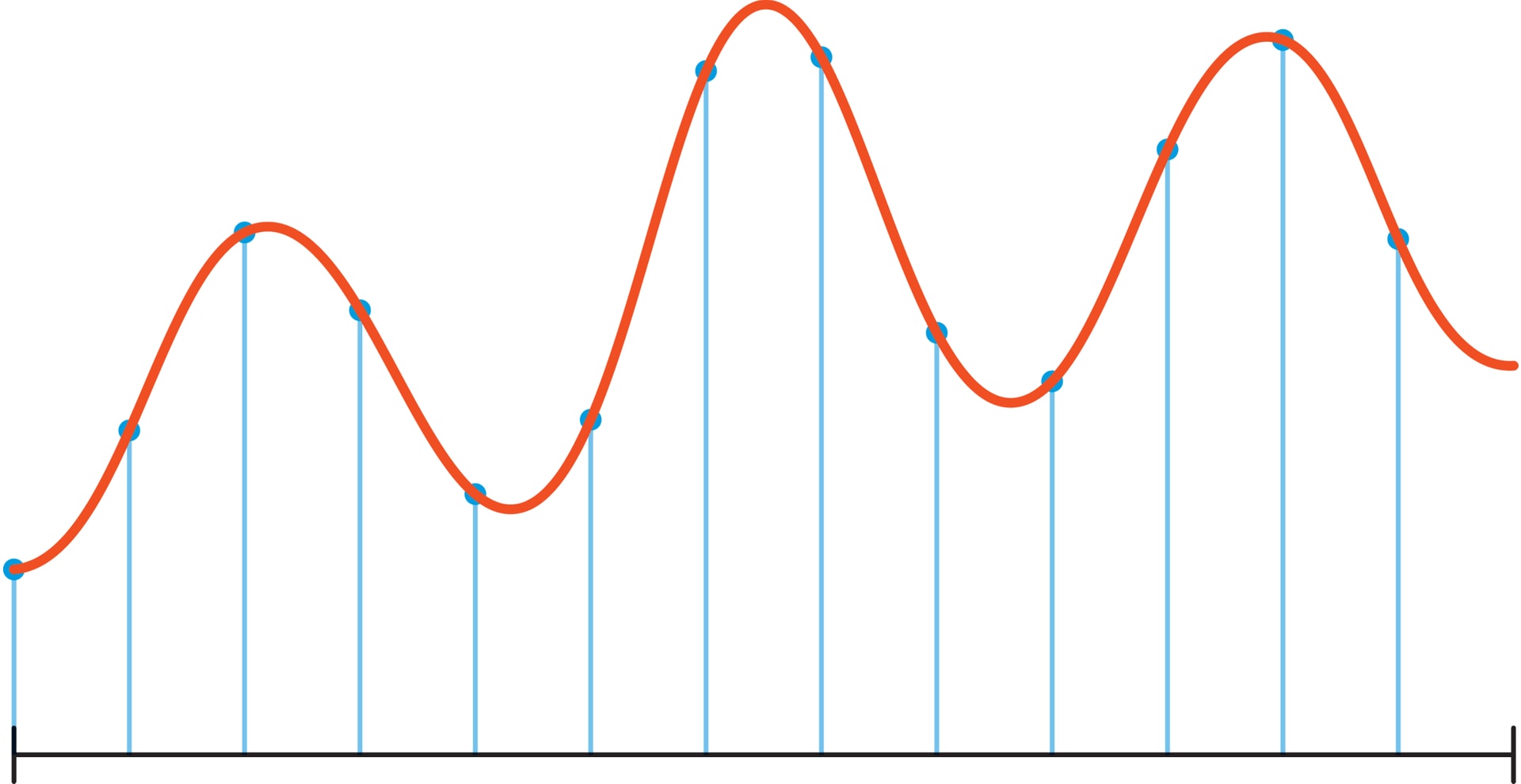
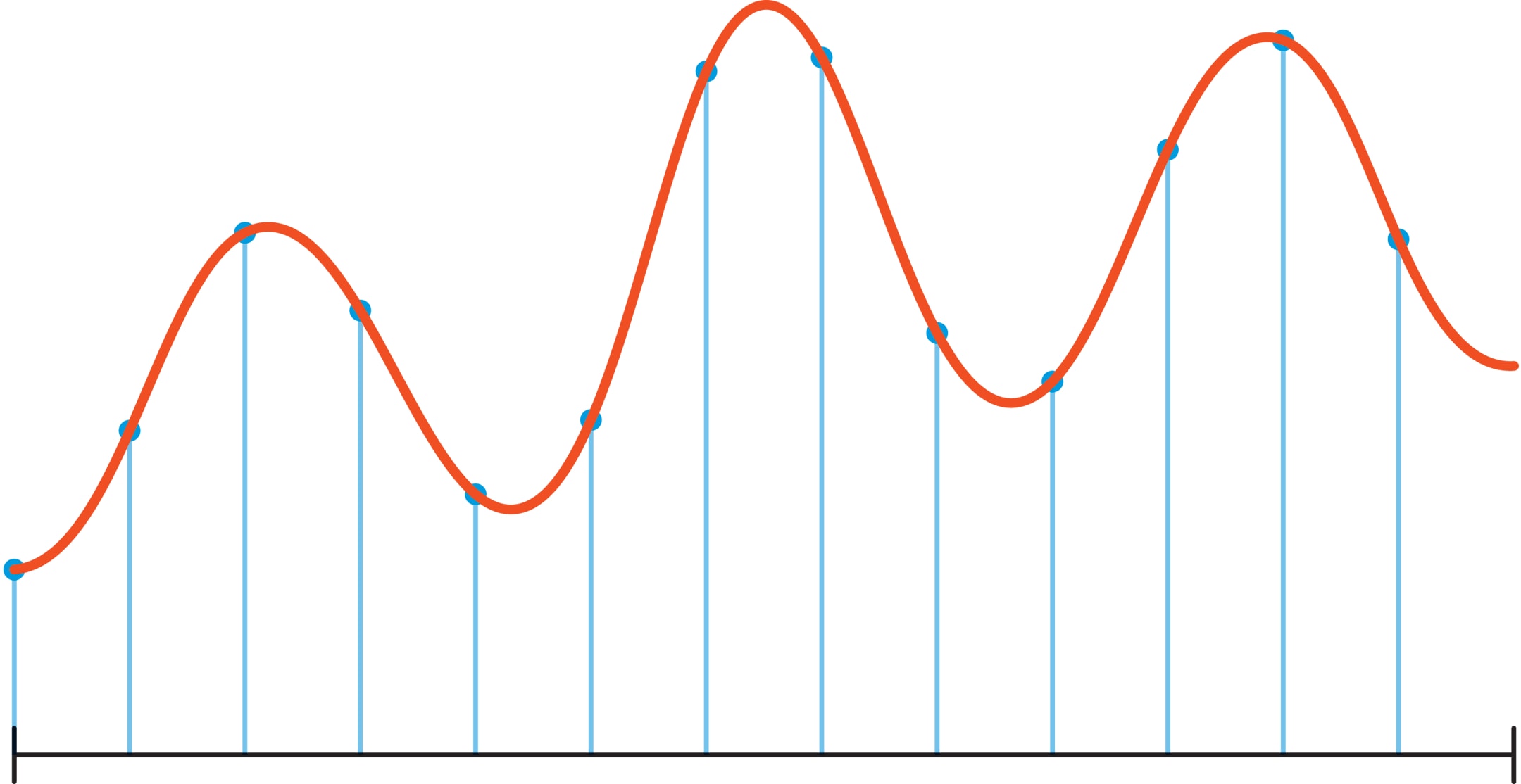
Типичный непрерывный сигнал, например звук или изображение, можно представить непрерывной функцией $f(t)$ на отрезке $[0,1]$ (или на прямой). Дискретный вариант — значения этой функции на частой равномерной сетке отрезка $[0,1]$, т. е. вектор $$ x={ \left( f{ \left( \frac 0N \right)},f{ \left( \frac 1N\right)},…,f{ \left(\frac { N-1 }N \right ) }\right)}. $$
Хранить такой сигнал в «необработанном» виде — дорого и неэффективно. Например, фотография, сделанная рядовым смартфоном, — это 10 мегапикселей, 10 миллионов точек, для обработки получается большое число $N$ порядка $10^7$. При обработке векторов такого размера суммарное количество операций будет гигантским. Проблему не решит даже использование архивации. Значит, необходимо найти какой‐то способ представления сигнала без значимых потерь в качестве (а иногда и с улучшением!), используя существенно меньшее, чем $N$, число параметров.
Однако задачу «экономного» представления сигнала без потерь не решить, если рассматривать любые сигналы, если не сузить их множество, предполагая наличие у них каких-то свойств. Сравните: бесполезно разрабатывать общую схему размещения 10 кубометров груза в багажнике объёмом 1 кубометр, если про характер груза ничего не известно.
Выручает то, что звуки, изображения и другие сигналы, взятые из жизни, обладают некоторой регулярностью, большую часть времени меняются плавно. Как выясняется, для представления плавно меняющихся сигналов число параметров можно значительно уменьшить.
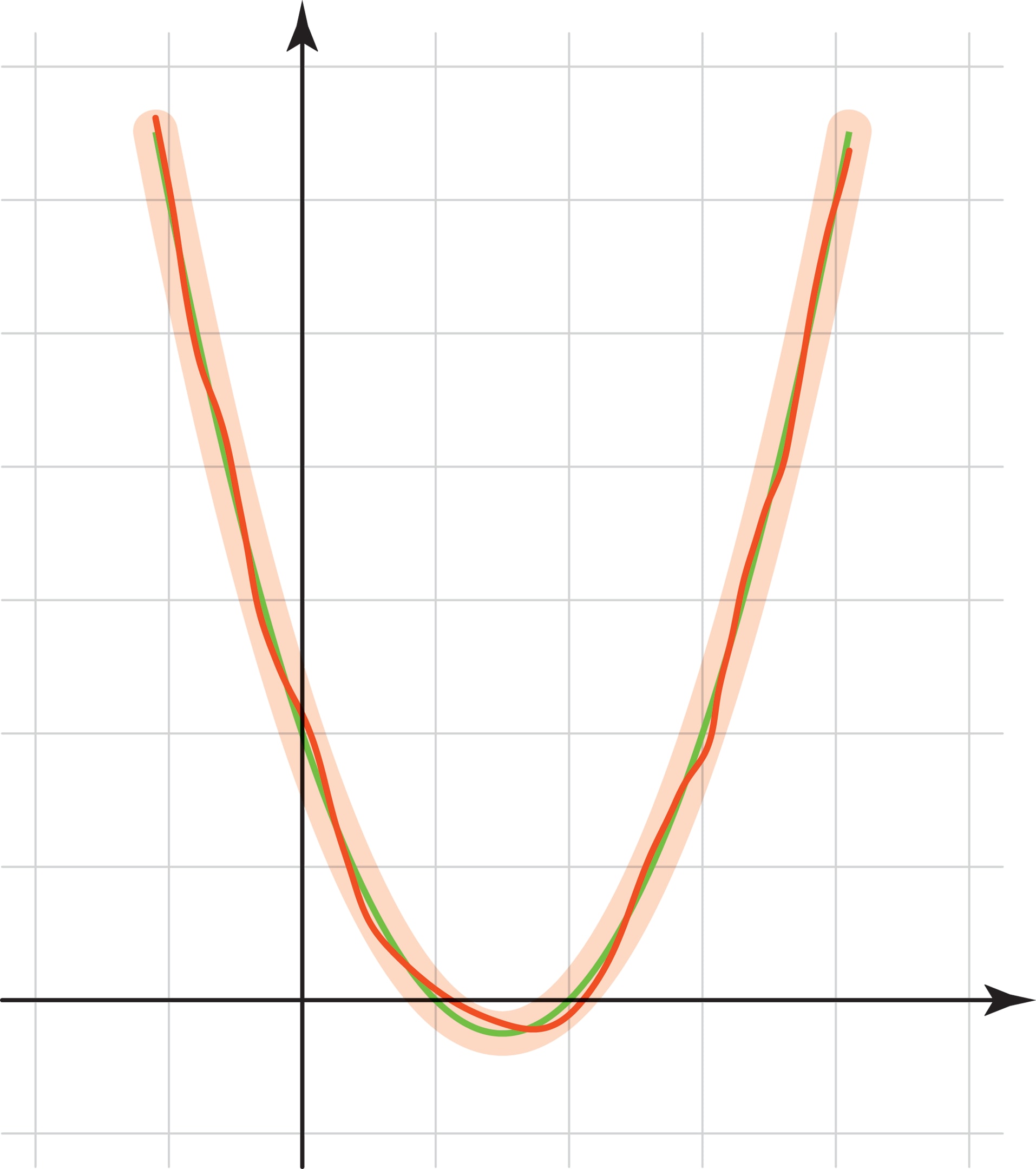
Теория приближения функций. Основная идея теории приближений — заменить «сложную» функцию $f(t)$ близкой к ней более простой функцией, являющейся линейной комбинацией выбранных заранее «базисных» функций. (Линейной комбинацией называется конечная сумма слагаемых, каждое из которых — одна из базисных функций, умноженная на какое-то число. Сам базисный набор может быть и бесконечным.) Если удастся найти приближение с точностью, необходимой для практических нужд, то можно передавать не гигантский набор значений $f(t)$ в $N$ точках, а скромный по численности набор коэффициентов при базисных элементах в приближении. По полученному набору коэффициентов функция может быть восстановлена с выбранной точностью.
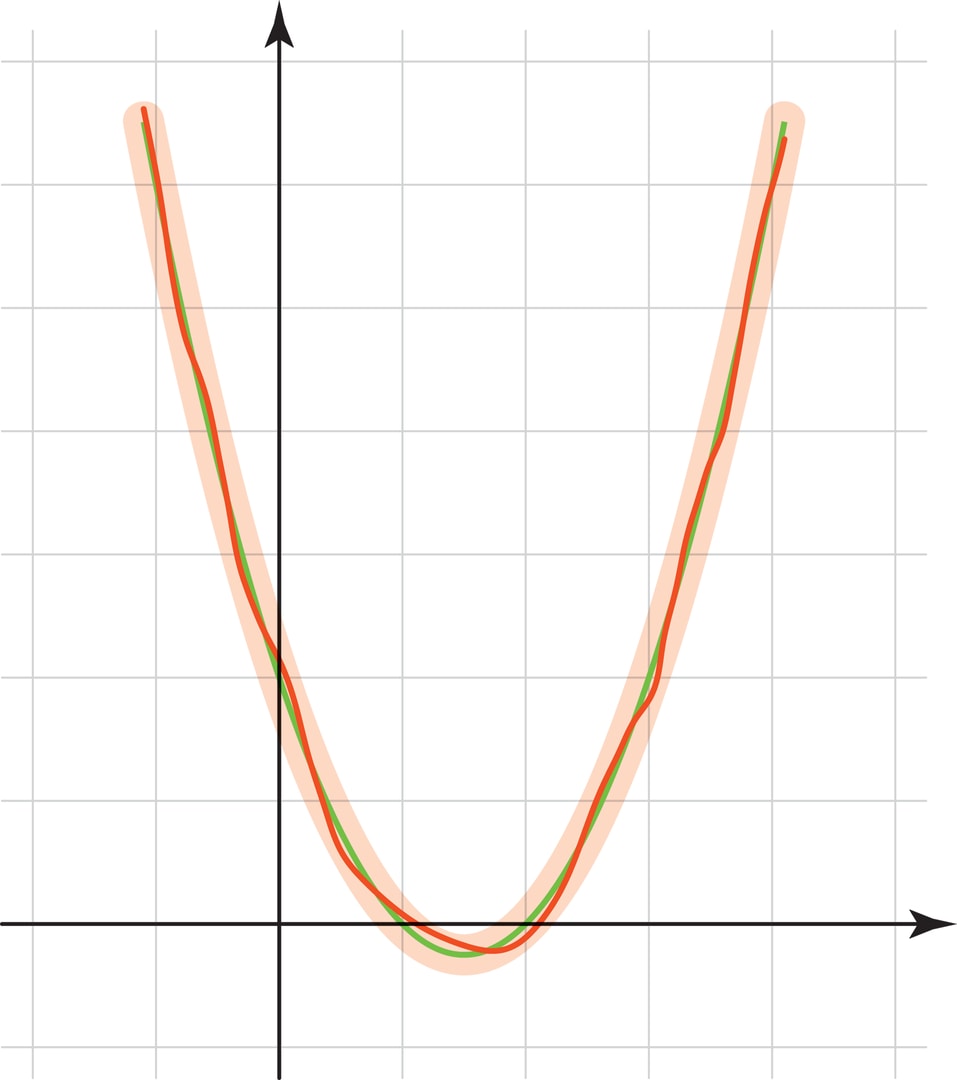
Например, в качестве базисного набора можно взять степени $t$: $\{1, t, t^2, t^3, …\}$. Их линейные комбинации — это известные читателю по школьному курсу математики многочлены. И если функция $y=f(t)$ такова, что её график мало отличается от параболы $y=t^2-3t+2$, то можно хранить только три числа: 1, -3, 2. (С идеей приближения непрерывной функции многочленами читатель встречался в сюжете «Гладкие линии».)
Ещё одна система, доказавшая свою эффективность во многих задачах, — тригонометрическая система функций, состоящая из целых сжатий синуса и косинуса: $\{\sin t$, $\cos t$, $\sin 2t$, $\cos 2t$, $… \}$. Данная система — основная в приближении периодических функций. Построение таких приближений 200 лет назад привело к созданию теории тригонометрических рядов Фурье.
Базисный набор выбирается в зависимости от решаемой практической задачи. Но к середине XX века стало ясно, что классические системы не соответствуют всем запросам. Возникла необходимость в новых конструкциях, которые должны соответствовать и естественным общим пожеланиям к базисному набору.
Одно из главных условий — базисные элементы должны быть максимально независимы, дополнять друг друга. Это обеспечит существенное улучшение точности приближения линейными комбинациями элементов базиса при его расширении.
Желательно также, чтобы для достижения заданной точности приближения было достаточно относительно небольшого числа базовых элементов, что может быть обеспечено быстрым убыванием погрешности при увеличении их числа.
Ещё одно пожелание к базовым элементам носит вычислительный характер. Важно, чтобы нахождение коэффициентов хорошего приближения было несложной и быстро решаемой задачей.
Одна из эффективных идей, возникших в математике в начале XX века, — изучать возможность приближения не отдельных функций, а целых классов функций, обладающих общими свойствами, например, одинаковых в смысле гладкости.
Геометрический взгляд. Приближения в выделенных классах непрерывных и дискретных сигналов настолько похожи, что изучение принципов и методов будет вестись поочерёдно, в зависимости от степени наглядности в том или ином случае.
Начать разговор проще с дискретного случая: вектор $x$ — не просто набор чисел, это точка геометрического пространства $\mathbb R^N$, которое можно представлять по аналогии с привычным трёхмерным пространством $\mathbb R^3$ с обычной евклидовой геометрией. Напомним, что в практических задачах размерность $\mathbb R^N$ — гигантская (например, $N\sim 10^7$).
Для дискретного сигнала на сетке с шагом $1/N$ изменение координат вектора будет плавным (гладким), если модуль разности двух соседних координат не превосходит $1/N$. И доля таких сигналов среди всех будет весьма небольшой. Все $N$‐мерные векторы, координаты которых неотрицательны и не превосходят единицы, образуют куб единичного объёма ($N$‐мерного). Среди них гладкие сигналы заполняют $N$‐мерный параллелепипед, его объём весьма мал и равен $(2/N)^{N-1}$. Наглядное представление — смартфон (прямоугольный, тонкий, почти плоский), лежащий на дне коробки кубической формы. Чтобы оценить долю гладких сигналов среди всех, рассмотрим модельный пример с фотографией, сделанной на смартфон: при $N=10^7$ объём параллелепипеда невозможно представить, он меньше, чем $1/10^{6 000 000}$.
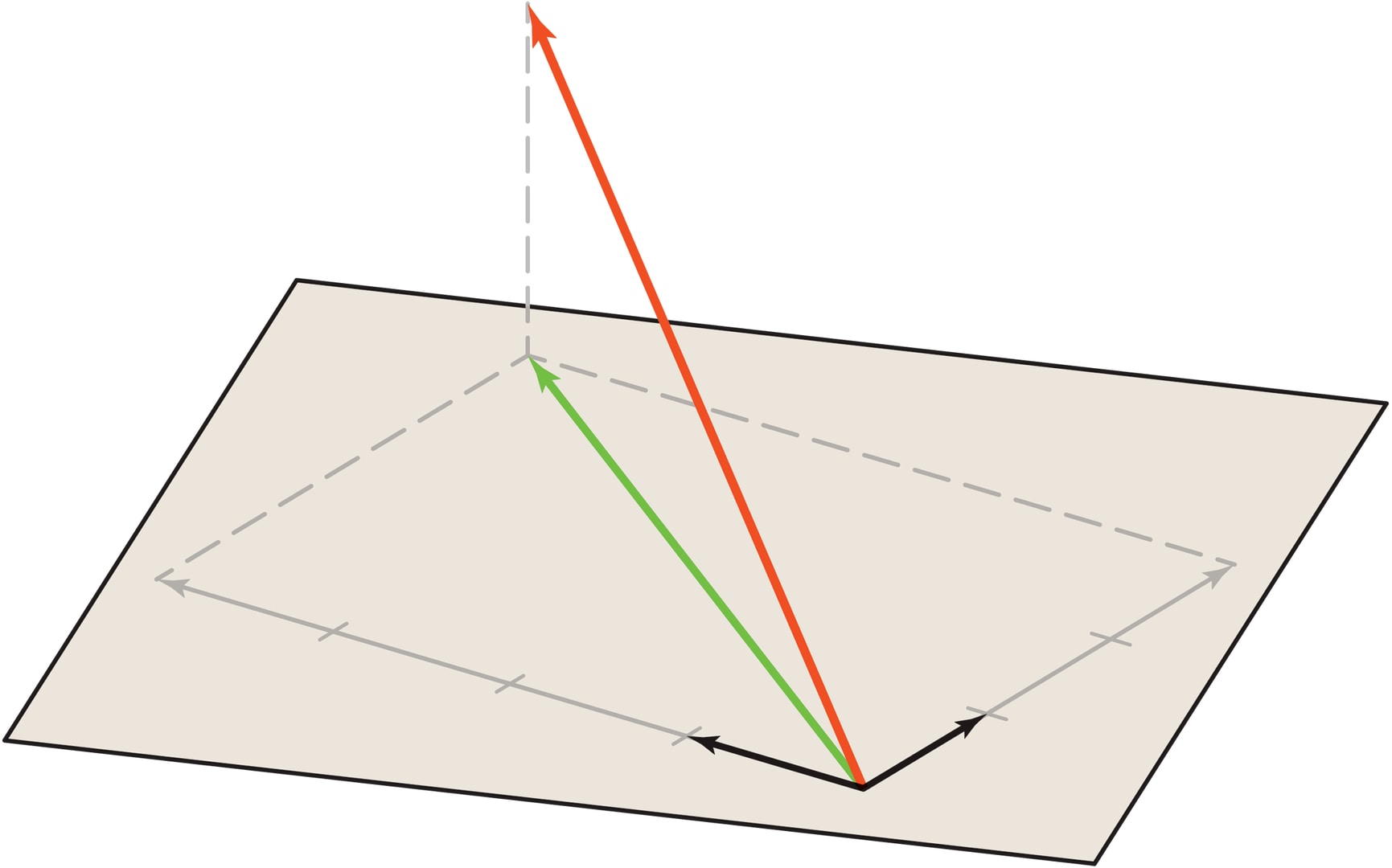
Итак, гладкие сигналы — мизерная часть множества произвольных сигналов. Описание всех гладких сигналов можно сделать достаточно «кратким», занимающим меньше памяти. Технически это означает, что можно найти базовые сигналы, число которых значительно меньше чем $N$, но линейными комбинациями которых («плоскостью», задаваемой ими) можно приблизить с достаточной точностью выбранный плавный сигнал (вспомните дно коробки как плоскость, в которой найдётся подходящее приближение для любой точки смартфона). Более общий случай: выпуклое тело малого объёма в $\mathbb R^N$ можно приблизить плоскостью, размерность которой меньше, чем $N$; причём чем меньше объём, тем лучше приближение (при фиксированной размерности плоскости). Приблизить — означает провести плоскость так, чтобы она проходила рядом с каждой точкой выпуклого тела, т. е. чтобы расстояние от каждой точки тела до плоскости было мало.
Для реализации идеи остаётся выбрать базис сигналов, который порождает плоскость, хорошо приближающую данное выпуклое тело гладких сигналов.
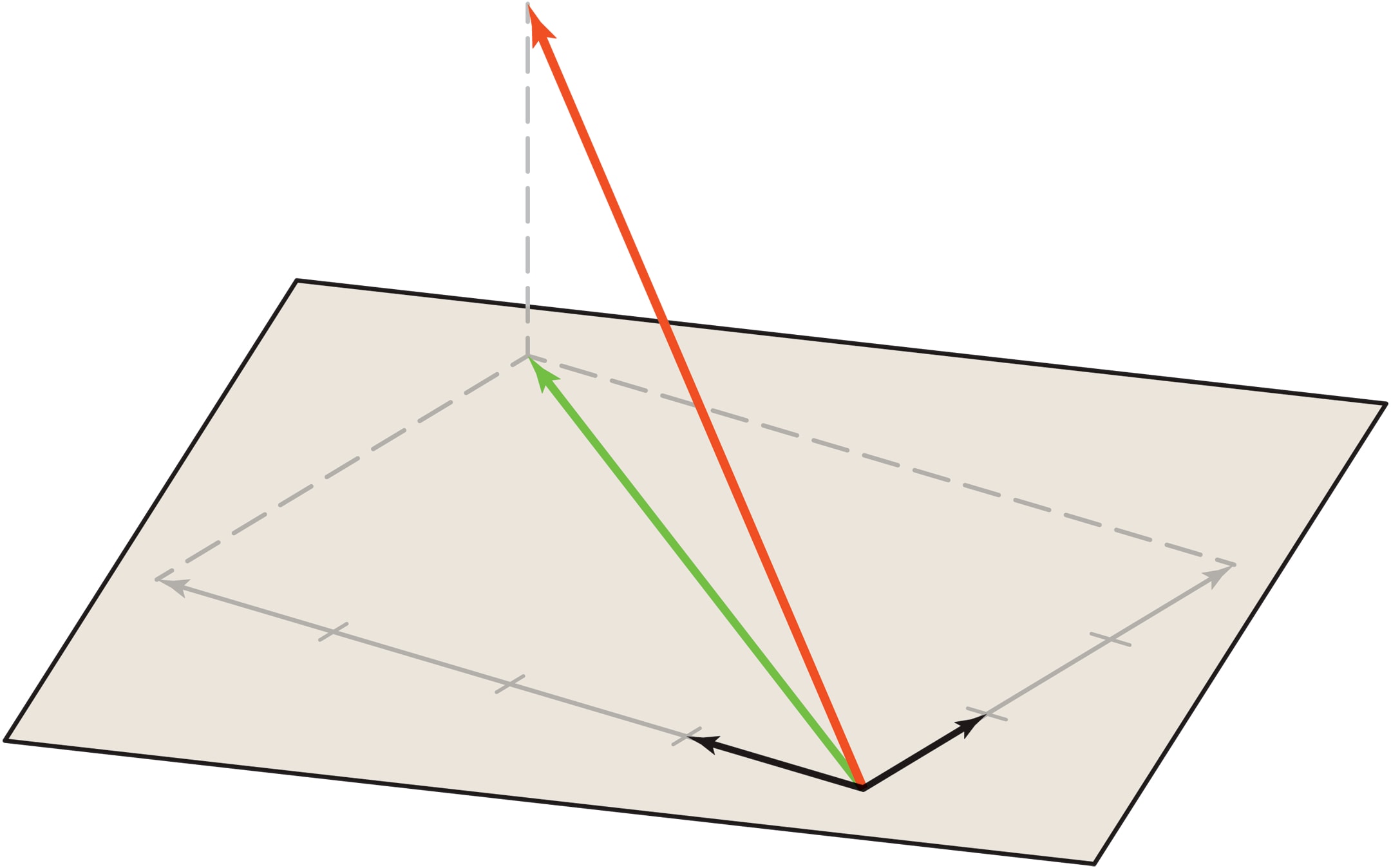
Работа в $\mathbb R^N$ с этим базисом будет значительно удобнее, если все базисные векторы $\{e_k\}$ будут попарно ортогональны (перпендикулярны) и нормированы (единичной длины): скалярные произведения $(e_i,e_j)=0$, если $i\ne j$, и $(e_i,e_i)=1$ при любом $i$. В этом случае отыскание наилучшего приближающего элемента «автоматизируется». Во‐первых, это проекция вектора на плоскость. Во‐вторых, проекция равна $\sum \mathord(x, e_k) e_k$, т. е. коэффициенты при таком разложении приближающего элемента по базису — скалярные произведения вектора $x$ и базисных векторов $e_k$.
Пространства гладких функций. В этом разделе есть «страшные» формулы, но «начинающий» математик может воспринимать их как иллюстрации.
Для непрерывных сигналов гладкость — мера плавности изменения функции. Простой непрерывности на практике недостаточно, разумно-минимальная степень гладкости — свойство липшицевости функции (которое уже встречалось в дискретном случае). Предполагается, что расстояние между двумя точками не может увеличиться больше, чем в заданное число раз, т. е. найдётся такое число $L$, что при любых $t_1$ и $t_2$ выполняется неравенство $$|f(t_1)-f(t_2)|\le L|t_1-t_2|.$$
Можно считать, что $L$ — характеристика растяжения резиновой нити на отрезке $[0,1]$, с помощью которой «изготовили» график функции $f(t)$. Липшицевость — существенное усиление простой непрерывности, но более слабое свойство, чем непрерывность производной $f'(t)$ во всех точках.
В пространстве непрерывных функций $C[a,b]$ естественное понятие расстояния между функциями $f$ и $g$ связано с близостью их графиков во всех точках: $$ d(f,g)=\max\limits_{t\in [a,b]} |f(t)-g(t)|.$$
Расстояние от $f$ до нулевой функции называется нормой: $$ \|f\|=\max\limits_t |f(t)|, $$
следовательно, $$d(f,g)=\|f-g\|.$$
(Это расстояние называют иногда чебышёвским, в честь Пафнутия Львовича Чебышева — основоположника теории приближения функций.) Это расстояние можно использовать и в классах $C^r[a,b]$, состоящих из $r$ раз дифференцируемых функций, у которых старшая производная $f^{(r)}(t)$ непрерывна на отрезке $[a,b]$. Введённое понятие расстояния позволяет оценить достижимую точность приближения в зависимости от гладкости функции.
Например, можно утверждать (теорема Джексона), что для $2π$-периодической функции $f\in C^r[0,2π]$ найдётся тригонометрический многочлен $f_n$ степени $n$ (элемент плоскости, порождённой функциями $\cos kt$ и $\sin kt$ при $k=0$, 1, …, $n$), расстояние от которого до $f$, т. е. $||f-f_n||$, имеет порядок $1/n^r$.
Мы уже говорили о том, что в $\mathbb R^N$ можно ввести скалярное произведение и сделать его похожим по устройству на $\mathbb R^3$. Но можно развить эту геометрическую идею и ввести бесконечномерные пространства со скалярным произведением. Пожалуй, самый важный пример — это класс функций на отрезке $[a,b]$ (достаточно широкий, например, в него входят все непрерывные функции), на этом классе скалярное произведение и норма функции (длина элемента) определяются формулами $$ \textstyle (f,g)=\int\limits_a^b f(t) g(t) dt, \qquad \|f\|=\sqrt{(f,f)}. $$
В результате мир функций становится геометрическим, в нём можно измерять расстояния и углы между функциями. Например, угол между $f(t)=t$ и $g(t)=2t$ равен нулю, эти векторы сонаправлены. Включение в базисный набор подобных функций, дублирующих друг друга, бессмысленно. А если равно нулю скалярное произведение функций, то функции называются ортогональными, они направлены в разные стороны, дополняют друг друга. Оказывается, что все функции из множества $\{1, \sin t, \cos t, \sin 2t, \cos2t, …\}$ попарно ортогональны на $[0,2π]$. В теории приближений появление ортогонального набора элементов — знак качества, оптимальности, совершенства системы.
В пространстве функций со скалярным произведением работают те же методы приближения (проекции), что и в $\mathbb R^N$.
Метод Фурье. Стандартный базис — ортогональная и нормированная (ортонормированная) система функций $\{e_j\}_{j\ge 0}$: $$ e_0=\frac{1}{\sqrt{2π}}, \quad e_{2k-1}=\frac{1}{\sqrt{\vphantom2π}} \cos kt, \quad e_{2k}=\frac{1}{\sqrt{\vphantom2π}} \sin kt. $$
Плоскость $V_n$, порождаемая функциями $\{e_0, e_1, …, e_{2n}\}$, состоит из тригонометрических многочленов степени $n$, т. е. функций вида $\sum\limits_{k=0}^n \mathord(a_k\cos kx + b_k \sin kx)$. Подпространства $V_n$ расширяются с ростом $n$ и в некотором смысле исчерпывают всё пространство функций. Точнее, для любой функции из этого пространства можно найти её приближение из некоторого $V_n$ с заданной точностью. Наилучшее приближение из $V_n$ — это проекция $f$ на эту плоскость $$ S_n f=\sum\limits_{k=0}^{2n} \mathord(f, e_k) e_k. $$
Как и в $\mathbb R^N$, способ нахождения коэффициентов в разложении проекции — универсальный, это вычисление скалярных произведений $(f, e_k)$.
В пространстве функций ортонормированная система $\{e_k\}_{k\ge 0}$ играет важную роль, тригонометрическими многочленами успешно приближаются гладкие функции (выпуклое множество в пространстве функций). Например, для функции $f$ класса $C^r[0,2π]$ с помощью теоремы Джексона несложно установить, что погрешность $\|f-S_nf\|$ имеет порядок $1/n^r$.
Теорема Джексона позволяет оценить число коэффициентов, которые нужно сохранить вместо оригинального сигнала, чтобы обеспечить необходимую точность. Это число гораздо меньше, чем количество значений на сетке. И чем выше гладкость сигнала, тем меньше понадобится для него коэффициентов. Например, если точность приближения $\varepsilon=0{,}01$, то при $r=1$ (что соответствует часто встречающимся липшицевым сигналам) такую погрешность обеспечивает 201 коэффициент. А если $r=3$ (такие сигналы встречаются гораздо реже) вся «посылка» будет состоять из 11 чисел!
Если функция и приближающий её тригонометрический многочлен отличаются мало, то номера входящих в него гармоник (синусов и косинусов) определяют спектр частот, из которых в действительности составлен сигнал. А коэффициенты в многочлене говорят о вкладе, который вносят соответствующие гармоники. Наглядный пример: тембр звука складывается из синусоидальных колебаний струны, коэффициенты в разложении — амплитуды, громкость (см. «Чистые интервалы»).
Дискретное преобразование Фурье. Идею замены непрерывного сигнала $N$-мерным вектором, компоненты которого — значения функции на сетке с шагом $1/N$, можно применить и к базисным наборам, например к тригонометрическим функциям. Свойства тригонометрической системы — ортонормированность и «базисные» способности — сохраняются и в «дискретном» варианте: получается ортонормированная система $\{E_k\}$ из $N$ векторов в $\mathbb R^N$. (Техническое изящество конструкции достигается заменой каждой пары $\{\cos kt, \sin kt\}$ двумя экспонентами $e^{\pm ikt}$; основа этой операции — формула Эйлера $e^{it}=\cos t + i\sin t$.)
Коэффициенты в разложении дискретного сигнала $x$ (вектора из $\mathbb R^N$) по базису $\{E_k\}$ образуют $N$-мерный вектор $\widehat x$, который называют дискретным преобразованием Фурье. На этом шаге экономии нет: просто один $N$‐мерный вектор превратили в другой.
Но если $x$ — сигнал гладкий, то координаты вектора $\widehat x$ с большими номерами малы. Отбросив их (т. е. заменив нулями, которые не нужно передавать), можно получить хорошее, но «короткое» приближение для вектора $\widehat x$. Применив обратное дискретное преобразование Фурье к этому приближению, получим вектор, хорошо приближающий сигнал $x$. Это основано на двух свойствах базиса $\{E_k\}$, унаследованных от непрерывного базиса $\{e_k\}$. Во‐первых, обратное преобразование Фурье вычисляется по тем же формулам, что и прямое (единственное изменение — замена знаков в показателе экспонент). Во‐вторых, дискретное преобразование Фурье — движение евклидова пространства $\mathbb R^N$, при котором сохраняются скалярные произведения $(\widehat x, \widehat y)=(x,y)$, а следовательно, и длины, и углы, и погрешности приближения.
Для оценки точности приближения сигнала с помощью дискретного преобразования Фурье можно воспользоваться дискретной версией теоремы Джексона. Оказывается, при $N=10^7$ и заданной точности $\varepsilon=0{,}01$ для случая $r=1$ (липшицевы сигналы) придётся вычислить примерно $6\cdot 10^5$ коэффициентов Фурье, а для $r=3$ — примерно 140.
Типичное сжатие по методу Фурье — примерно в 10—20 раз (число $N=10^7$ заменяется на $6\cdot 10^5$). Но чтобы этот выигрыш получить, придётся вычислять десятки тысяч коэффициентов Фурье, а это означает выполнение $2N^2$ арифметических операций.
Например, при $N=10^7$ получается «нереальное» значение $2\cdot 10^{14}$. Отправка фотографии, сделанной смартфоном, заняла бы… более получаса! А ведь потом ещё придётся потратить столько же времени на раскодировку, т. е. на обратное преобразование Фурье. Конечно, нам нужны не все коэффициенты Фурье, при гладком сигнале их число уменьшается, но и тогда объём вычислений получается недопустимо большим.
Неужели из этой ситуации нет никакого выхода? Оказывается, существует специальный алгоритм, который даёт возможность находить коэффициенты Фурье не по отдельности (один за другим), а параллельно. Это — быстрое преобразование Фурье, в котором вычисления устроены так, что их результаты используются для определения сразу нескольких коэффициентов Фурье (аналогия — быстрое умножение, см. «Быстрая арифметика». Экономия получается существенной: число операций сокращается с $2N^2$ до $2N\log_2 N$. Например, при $N=10^7$ необходимо выполнить не $2\cdot 10^{14}$ операций, а менее $5\cdot 10^8$ — выигрыш в $400 000$ раз! Отправка фотографии займёт долю секунды!
Вывод, который необходимо сделать, такой: при построении приближения надо учитывать не только количество используемых коэффициентов Фурье, но и число операций при их вычислении. Заметим, что в задаче разложения по базису из $N$ элементов число операций (сложность, см. «Теория сложности») не может быть меньше чем $N$. Действительно, для определения каждого коэффициента нужна хотя бы одна операция. Сложность метода быстрого преобразования Фурье является почти линейной, т. е. близка к границам возможного.
Недостаток тригонометрической системы. Выбор тригонометрических функций в качестве базисных для обработки гладких сигналов удачен во многих отношениях, от эффективности до удобства. Эффективность — высокий коэффициент сжатия — обеспечивается гладкостью тригонометрических функций и теоремой Джексона. Удобство связано и с общим свойством ортогональной системы — наилучшим приближением является проекция, и с тем, что коэффициенты разложения в проекции можно найти с помощью быстрого преобразования Фурье (вычислительная сложность близка к линейной). В целом метод Фурье хорош и широко применяется.
Но у тригонометрической системы есть серьёзный и неустранимый недостаток, который стал особенно заметен при использовании мощных компьютеров, — чувствительность к шуму.
Шум — искажение сигнала, ошибка. Как правило, это кратковременная, но большая по величине добавка к основному сигналу. Например: щелчок, треск — на пластинке, пылинка — на фотографии. Для дискретного сигнала $x$ шум — это изменение одной из его координат. Но в разложении Фурье сигнала $x$ изменятся все координаты вектора $\widehat x$ (на одну и ту же величину) — ошибка в одной координате размазалась равномерно по всем координатам $\widehat x$, замаскировалась. Поэтому найти место повреждения сигнала и исправить ошибку будет трудно. В результате при обработке методом Фурье зашумлённой фотографии получится менее чёткое, размытое изображение.
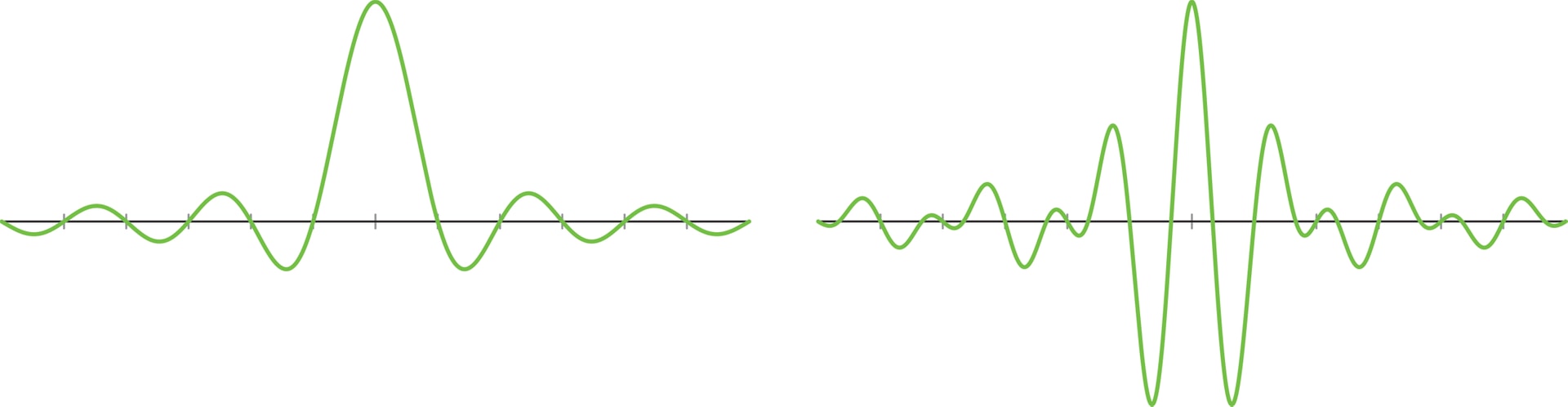
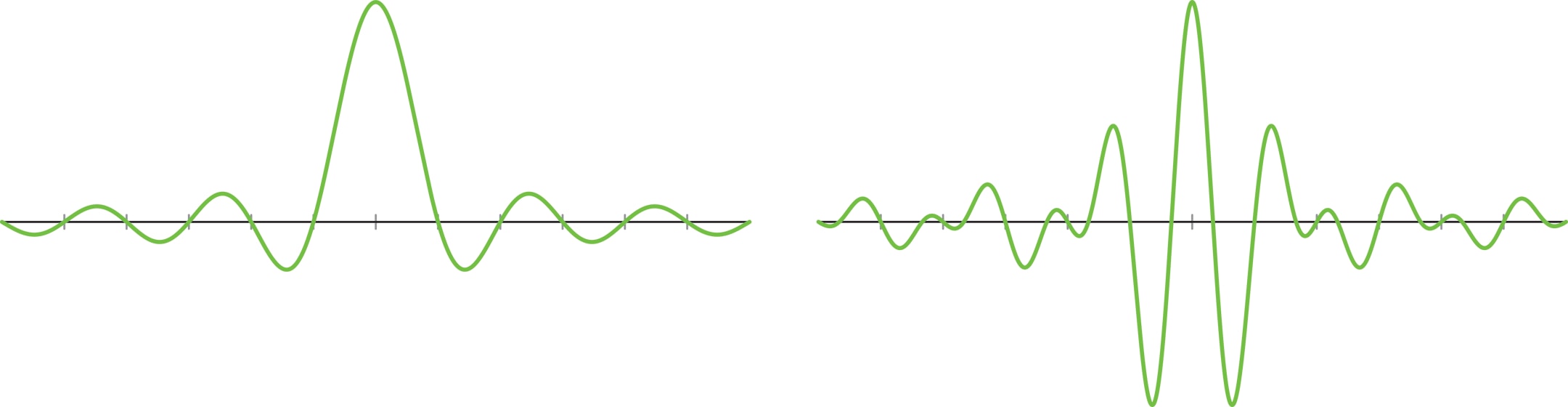
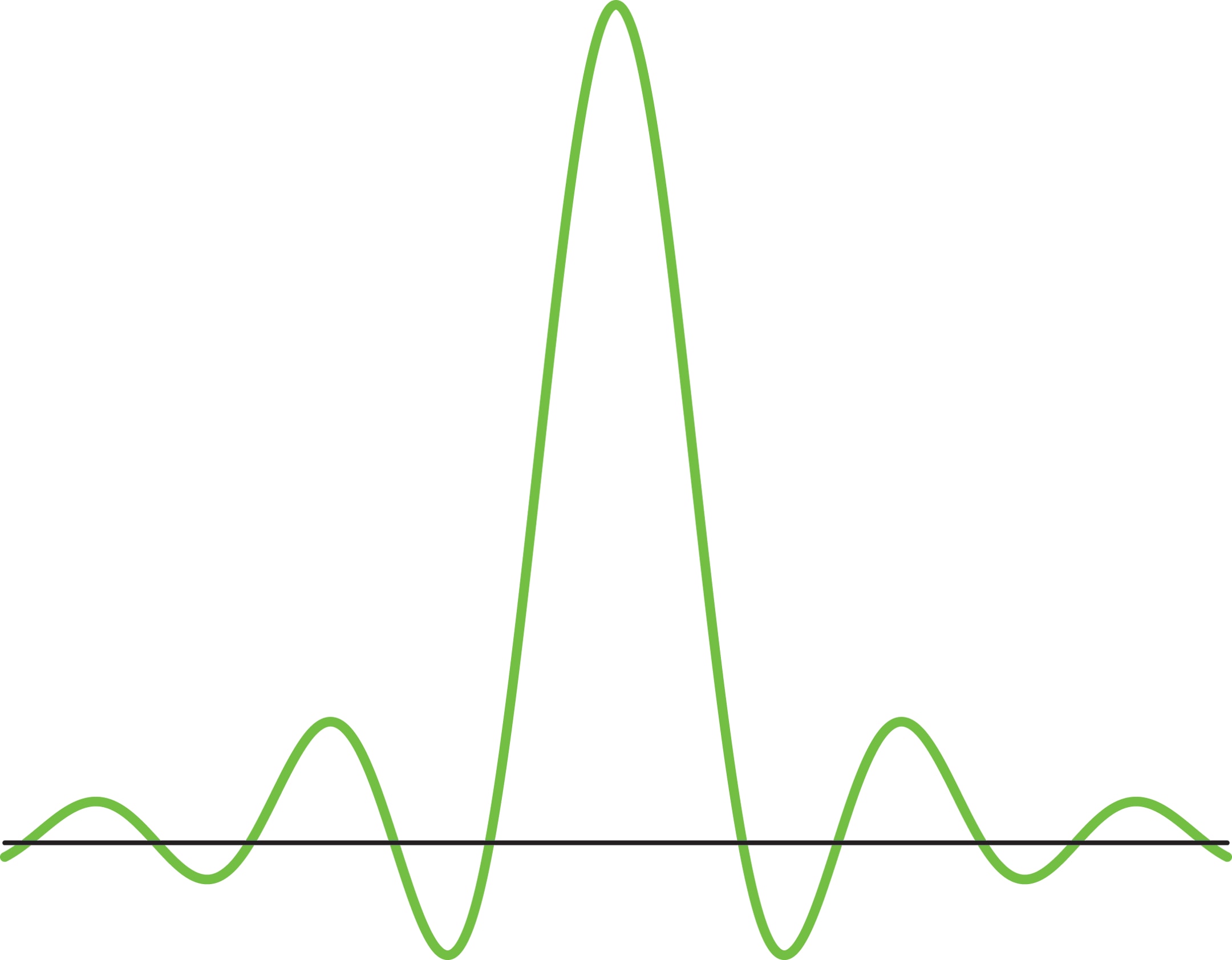
Чтобы избежать эффекта размазывания шума, надо найти и использовать базис, состоящий из локализованных функций. Так называется функция, у которой все ненулевые значения сосредоточены на небольшом отрезке. Иными словами, нужны не плавные волны типа синусов и косинусов, а резкие и узкие всплески.
Начало всплесков: система Хаара. На пути к базису эффективному и состоящему из локализованных функций сделаем промежуточную остановку в 1909 году и познакомимся с базисом Хаара. Этот базис удобен в использовании, состоит из локализованных функций, но при этом не очень удачен в смысле эффективности. Базис Хаара на отрезке $[0,1]$ строится последовательно, по уровням.
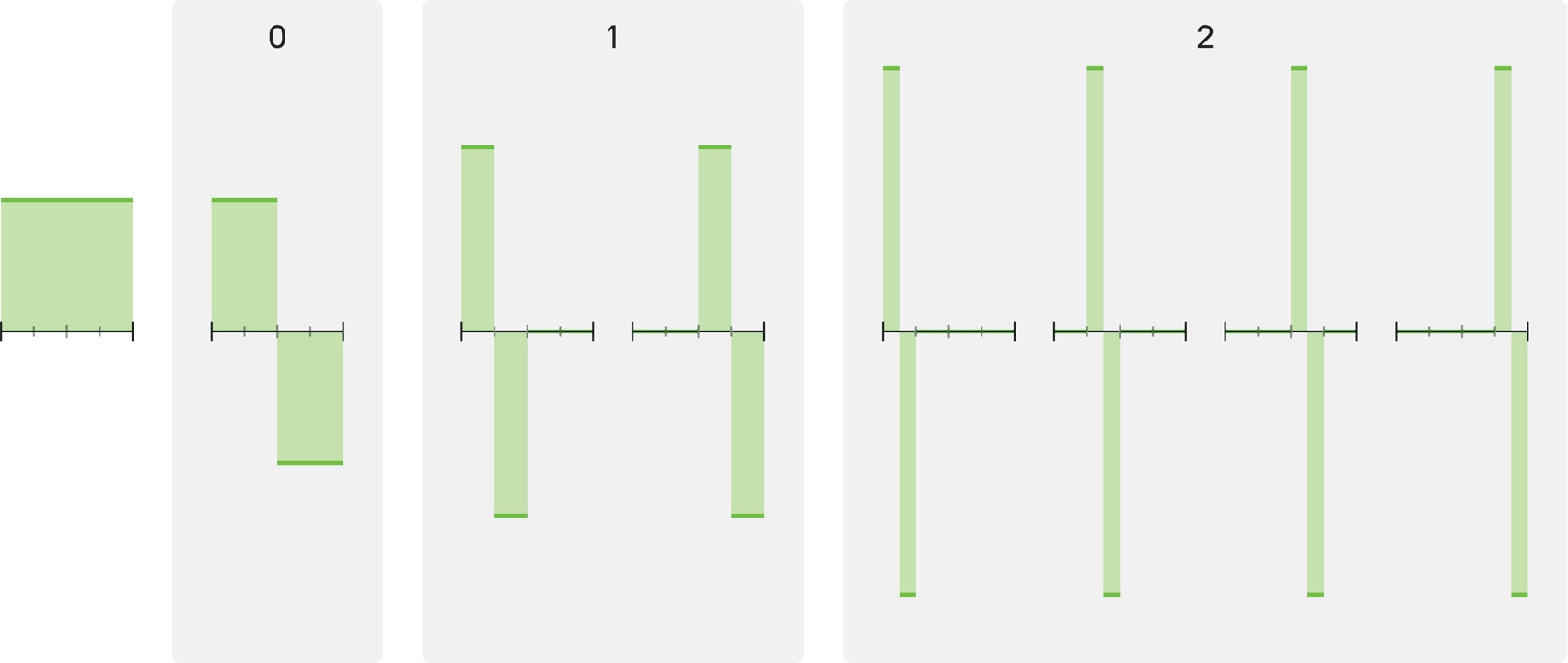
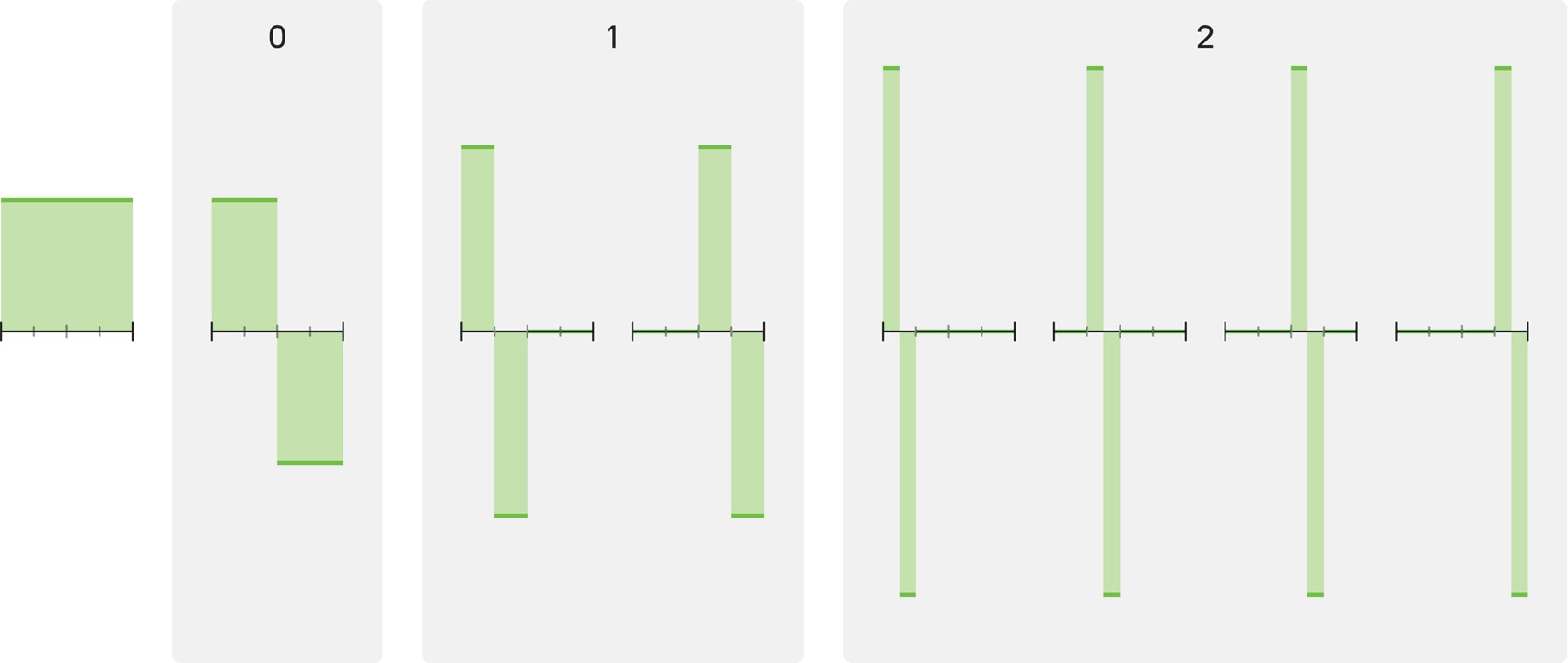
На нулевом уровне — всего одна функция $h_1$, «ступенька»: она равна 1 на левой половине отрезка и $(-1)$ — на правой. Из сжатий и сдвигов этой функции $h_1$ получаются все последующие функции Хаара.
На первом уровне обитают две функции, $h_2$ и $h_3$: сжатая в два раза ступенька $h_1$ может быть локализована и на $[0,1/2)$, и на $[1/2,1)$.
Функции ${h_4,h_5,h_6,h_7}$ второго уровня — это четыре ступеньки, полученные сжатием $h_1$ в четыре раза и локализованные на последовательных четвертях отрезка $[0,1]$.
В общем случае уровень с номером $n$ состоит из $2^n$ ступенек, каждая из которых — ступенька $h_1$, сжатая в $2^n$ раз.
Функции одного уровня попарно ортогональны, так как они расположены на непересекающихся отрезках. Ортогональность функций разного уровня доказывается несложно. Чтобы норма каждой функции была равна 1, надо каждую ступеньку умножить на коэффициент, учитывающий длину отрезка локализации.
Если функцию $h_1$, продолженную тождественным нулём на всю числовую прямую, обозначить через $\psi$, то все функции Хаара $\{h_k\}$ можно описать одной формулой: $2^{n/2}\>\psi(2^n t - k)$, где $n\ge 0$, а при фиксированном $n$ параметр $k$ меняется от 0 до $2^n-1$. Чтобы система стала ортонормированным базисом, надо добавить к ней ещё одну функцию $h_0= 1$.
В пространстве всех функций функции Хаара $\{h_k\}_{k=0}^{2^n-1}$ задают плоскость $V_n$ размерности $2^n$. Базис пространства $V_n$ — объединение функций всех уровней от 0 до $n-1$. Аналогично системе Фурье, наилучший элемент приближения функции $f$ в подпространстве $V_n$ — проекция $$\textstyle S_nf=\sum\limits_{k=0}^{2^n-1} (f, h_k) h_k.$$ При проецировании на $V_n$ любая функция $f$ превращается в «лесенку» из $2^n$ ступенек. Высота каждой ступеньки есть среднее значение функции на соответствующем интервале.
Дискретный вариант базиса Хаара $\{H_k\}$ — пронормированные значения функций $\{h_k\}$ на сетке с шагом $1/2^n$. Система $\{H_k\}_{k=0}^{2^n-1}$ — ортонормированный базис в $\mathbb R^N$, $N=2^n$.
Даже прямое вычисление всех коэффициентов в базисе $\{H_k\}$ имеет сложность вдвое меньшую, чем для быстрого преобразования Фурье. Это следствие двоичной структуры базиса Хаара. Но и эту низкую сложность можно уменьшить! В так называемом каскадном алгоритме используется фактическая повторяемость действий в дискретном преобразовании Хаара, обусловленная двоичностью и «правильным» чередованием знаков функций $\{H_k\}$. В итоге достигается сложность $4(N-1)$ — по порядку неулучшаемый результат, в среднем менее четырёх операций на каждый коэффициент!
В дискретном преобразовании Хаара, в отличие от преобразования Фурье, шум, появившийся в одной координате вектора $x$, меняет не все коэффициенты в разложении $x$ по базису $\{H_k\}_{k=0}^{2^n-1}$, а только $n+1$, по одной координате на каждом уровне. Число $n+1$ мало по сравнению с $N=2^n$, т. е. преобразование Хаара сохраняет локализованность помех.
Казалось бы, идеальная система, но… У базиса Хаара тоже есть недостатки. Главный из них — скорость приближения функции перестаёт расти с возрастанием гладкости. Например, функции класса $C^3$ приближаются не лучше, чем функции из класса $C^1$. Это ведёт к медленной сходимости разложений Хаара и, как следствие, к необходимости хранить большое число коэффициентов.
Другой недостаток функций Хаара — они разрывные. А это сужает технические возможности. Во многих приложениях приближение функции (сигнала) приходится дифференцировать, иногда даже несколько раз (скажем, при численном решении дифференциальных уравнений). С функциями Хаара этого делать нельзя, они не только не дифференцируемы, но и не непрерывны.
Значит, в идеале, для приближений нужен «гладкий Хаар»!
Всплески: общая конструкция. Мы двигались в изложении «параллельно» развитию теории приближений функций, пропустив ряд важных остановок — многочисленные достижения на этом пути. Накоплены идеи, благодаря которым в 1980-х годах произошла кристаллизация понимания того, как должны выглядеть всплески — «правильный» базис в пространстве функций со скалярным произведением на числовой прямой $\mathbb R$.
Общее представление базиса всплесков даётся на языке линейных пространств, плоскостей, которые порождаются конечными наборами элементов базиса. Терминологически такое представление называется кратномасштабным анализом: это система замкнутых подпространств $\{V_n\}_{n \in \mathbb Z}$ в пространстве функций, обладающая следующими свойствами.
1. Пространства $V_n$ расширяются: $V_n\subset V_{n+1}$, $V_n\ne V_{n+1}$.
2. Пространства $V_n$ «исчерпывают» всё пространство функций при $n\to \infty$: любую функцию можно приблизить сколь угодно точно функциями из некоторого пространства $V_n$.
3. Пересечение всех пространств $V_n$ содержит только нулевую функцию (тождественный нуль).
4. Расширение в системе $\{V_n\}$ носит двоичный характер: для любой функции $f(t)\in V_n$ имеем $f(2t)\in V_{n+1}$.
5. Пространство $V_0$ порождено ортогональными друг другу целыми сдвигами некоторой функции $\varphi$.
С помощью функции $\varphi$ можно построить всплеск-функцию $\psi$, сдвиги и сжатия которой образуют систему всплесков, являющуюся ортонормированным базисом в пространстве функций: $$\psi_{n , k} (t) = 2^{n/2}\> \psi(2^n t - k),\qquad n{,} k \in \mathbb Z.$$ Каждый кратномасштабный анализ порождает систему всплесков, и любая система всплесков порождается некоторым кратномасштабным анализом. Поэтому построение системы всплесков сводится к построению функции $\varphi$.
Базисы, порождаемые системами кратномасштабного анализа, в силу своей двоичной природы обладают рядом преимуществ. Во‐первых, коэффициенты разложения быстро вычисляются с использованием каскадного алгоритма. Во‐вторых, и это главное, переход от плоскости $V_n$ к $V_{n+1}$ означает, что в задаче о приближении число используемых базисных функций увеличивается вдвое, что является оптимальным способом достижения заданной точности.
Отметим, что условия на пространства $V_n$ в определении кратномасштабного анализа обеспечивают то, что система $\{\psi_{n, k} (t)\}$ будет базисом в пространстве функций на прямой.
Всплески: примеры. Построенный базис Хаара на отрезке $[0,1]$ — всё ещё не система всплесков. Он превращается в таковую с помощью распространения на всю прямую $\mathbb R$. Всплески Хаара порождаются функцией $\varphi$ — характеристической функцией промежутка $[0,1)$, которая равна 1 на нём и 0 вне него, а также функцией $\psi$, полученной продолжением нулём на $\mathbb R$ функции Хаара $h_1$. Всплески Хаара обладают прекрасной локализацией, но наследуют и недостатки системы Хаара (ограниченность скорости приближения при росте гладкости, разрывность функций системы).
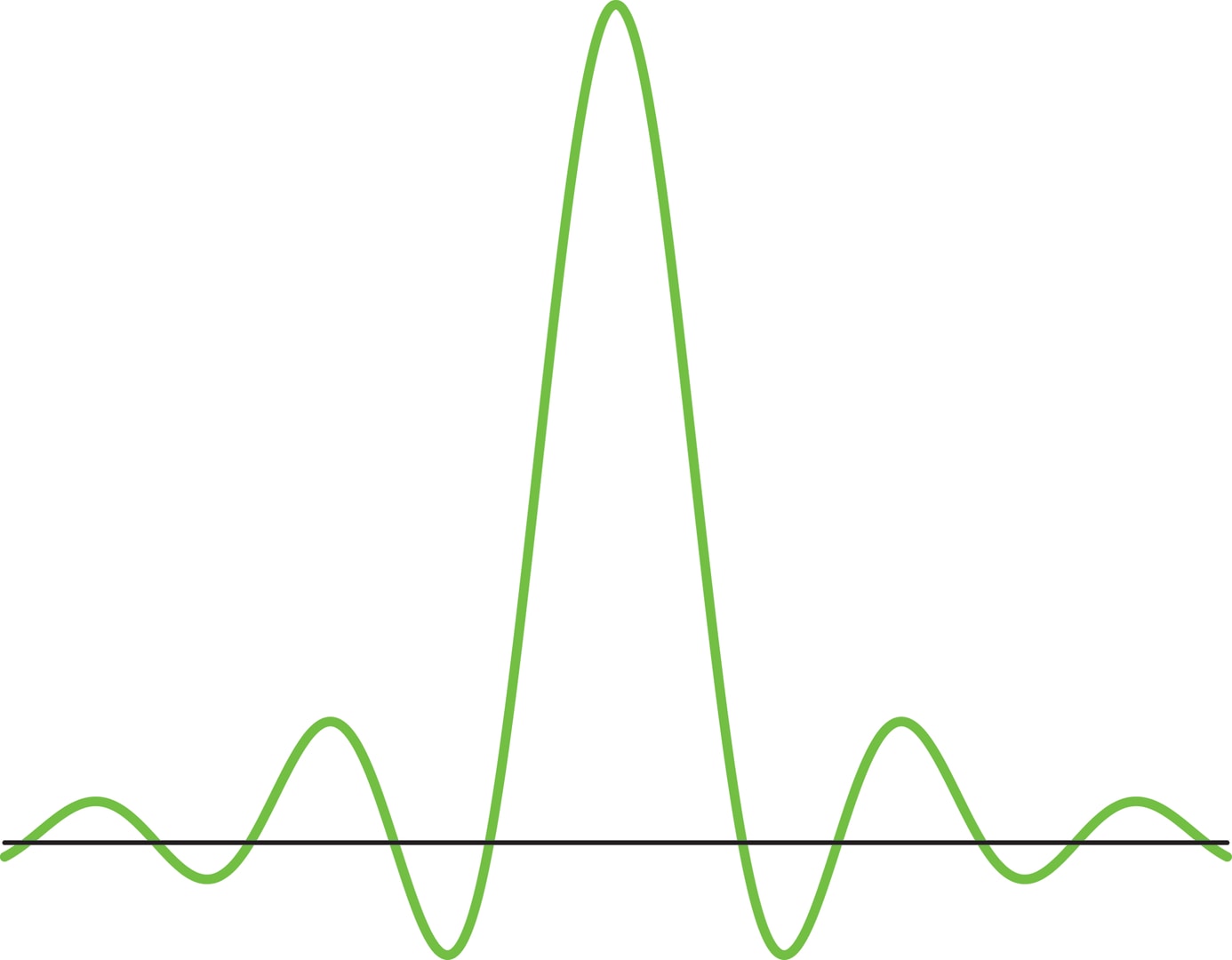
Всплески Шеннона—Котельникова достаточно естественным образом возникают в электронике, поэтому инженеры придумали эту систему раньше математиков (в первой половине XX века). Кратномасштабный анализ пространств функций порождён функцией $\varphi$ и соответствует системе всплесков с функцией $\psi$, где $$ \varphi (t)= \frac{\sin π t}{π t},\qquad \psi (t)= \frac{\sin 2π t - \sin π t}{π t}. $$
(Техническое пояснение для аналитиков: функция $\varphi$ — преобразование Фурье характеристической функции отрезка. Так что возникающая система всплесков в каком‐то смысле двойственна системе Хаара.)
Получающиеся всплески Шеннона—Котельникова очень гладкие, но при этом далеки от локализованных: медленно убывают при $t \to \infty$. Плохая локализация затрудняет избавление сигнала от шума и замедляет работу каскадного алгоритма. Это главный недостаток данной системы.
Всплески Мейера. В 1986 году Ив Мейер немного «подправил» систему Шеннона—Котельникова, получив гладкую и быстро убывающую систему всплесков. Эта малая поправка, однако, далась большими усилиями, ведь новая система должна была сохранить все свойства всплесков Шеннона—Котельникова. (Изменение можно пояснить так: в отличие от системы Шеннона—Котельникова, теперь функция $\varphi(t)$ является преобразованием Фурье сглаженной характеристической функции отрезка, а такая функция $\varphi(t)$ быстро убывает при $t \to \infty$.) Получилась замечательная система функций, которая до сих пор широко используется. В отличие от ранее известных систем, всплески Мейера не были взяты «из жизни», а полностью, от начала до конца, придуманы. Это — чисто математическая конструкция, причём очень хитрая и тонкая. За её изобретение Мейер получил множество научных наград, включая престижнейшую премию Абеля в 2017 году.
При всех своих достоинствах, всплески Мейера — это ещё не «гладкий Хаар», поскольку всплеск-функция не обращается в нуль вне некоторого отрезка (хотя и быстро стремится к нулю).
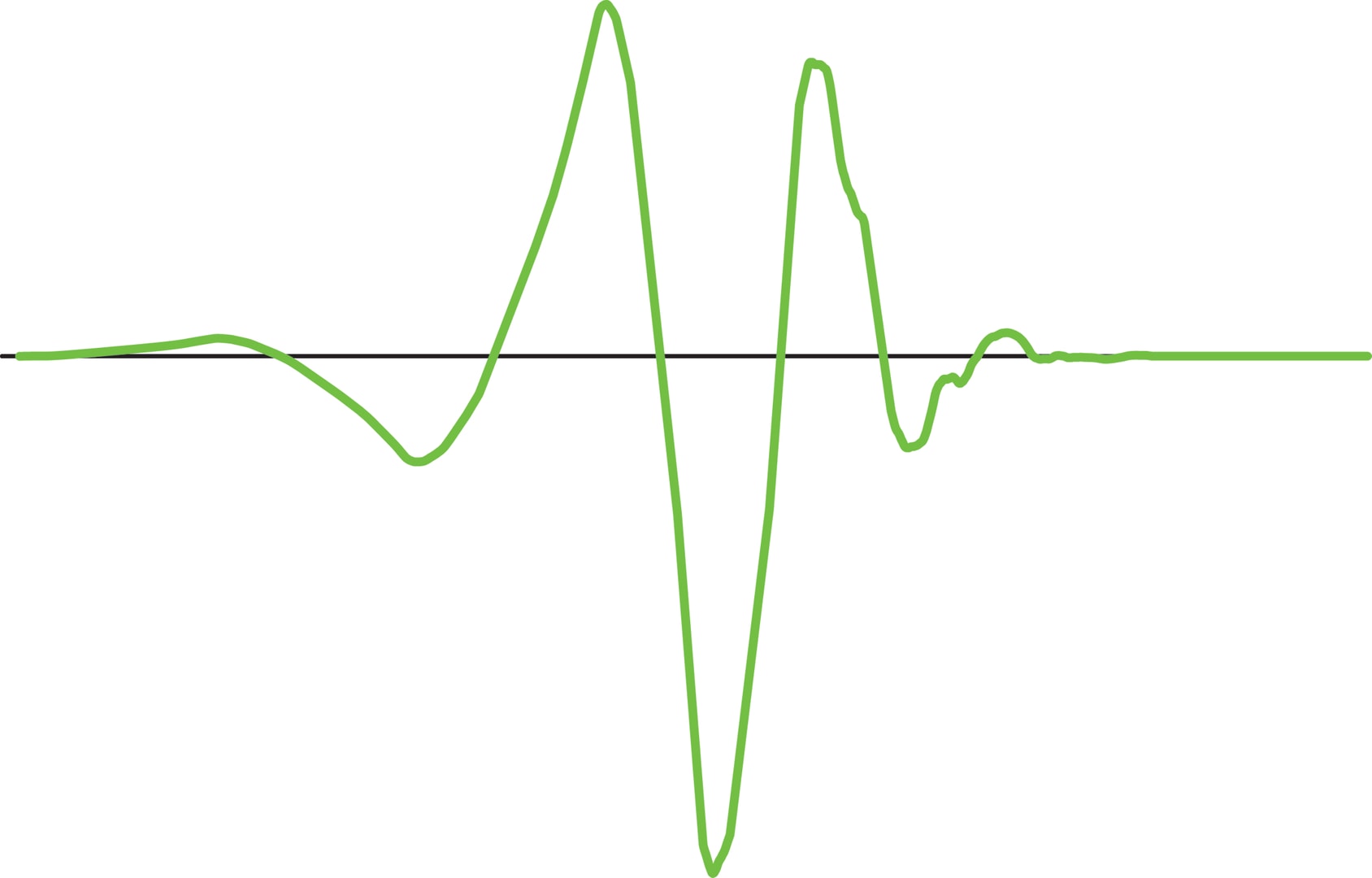
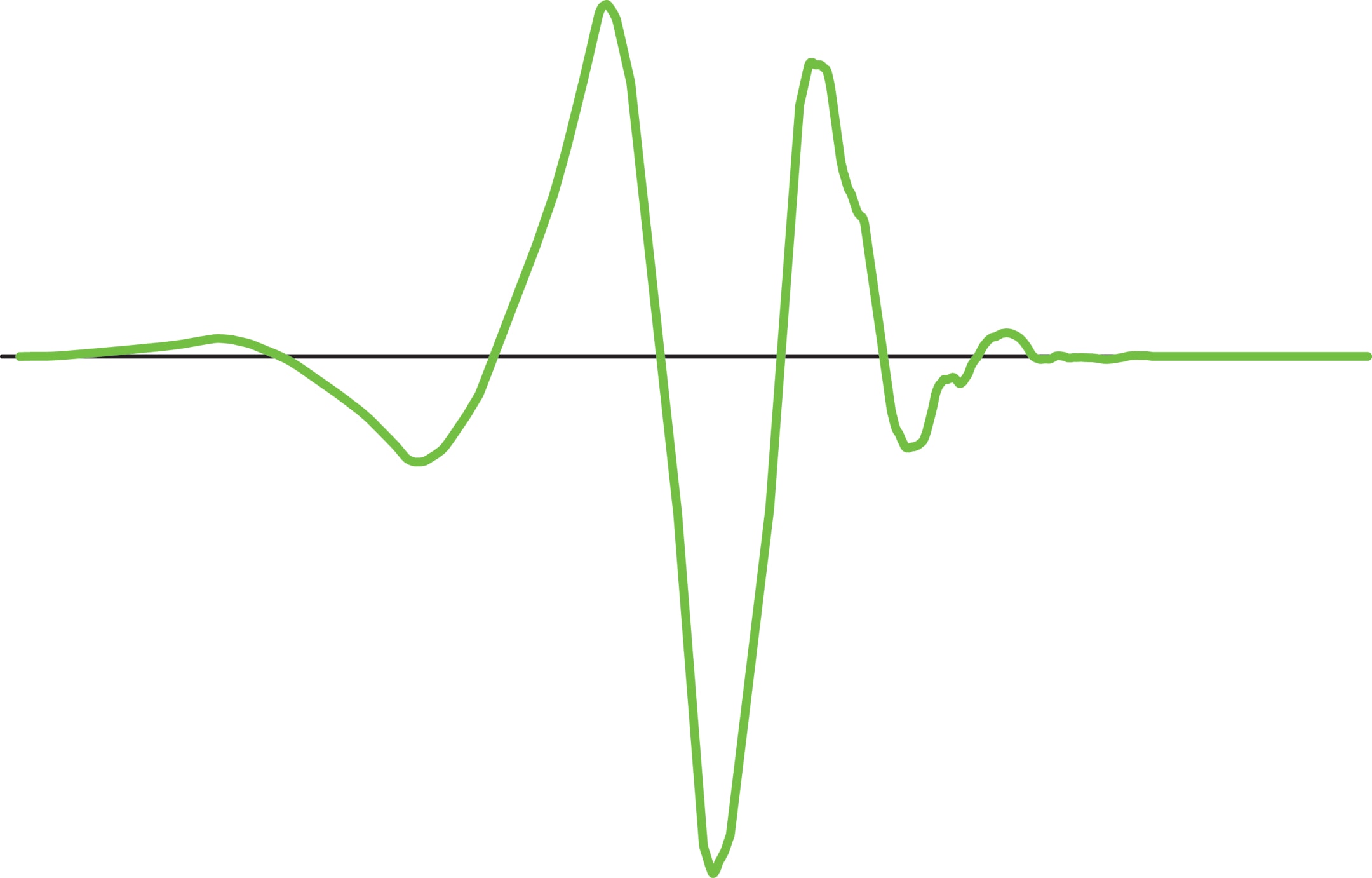
Всплески Добеши были изобретены в 1988 году и произвели сенсацию в научном сообществе. На Международном конгрессе математиков в Цюрихе в 1994 году Ингрид Добеши, вопреки обыкновению, было дано два часа для пленарного доклада, вместо принятого одного часа. Новые базисы уже не задаются явными формулами, а строятся как решения специальных уравнений. Вычисляются они приближённо с некоторой точностью. Базис ные функции имеют конечную гладкость, в отличие от систем Шеннона—Котельникова и Мейера. Более того, они имеют много общего с фракталами. Тем не менее они обладают всеми необходимыми свойствами: хорошо приближают сигналы и позволяют удалять шумы. А самое главное, как и для системы Хаара, функции системы Добеши сосредоточены на конечных отрезках. Сейчас они используются повсеместно при работе с фото- и видеоизображениями, в компьютерной томографии, при распознавании образов и т. д. Например, стандарт JPEG2000 основан на всплесках Добеши.
Заключение. Подведём итоги рассказа о задачах экономного представления сигналов. Два века назад появилась теория рядов Фурье. Столетием позже появились первые всплески (функции Хаара), ещё через 80 лет возникли всплески Добеши. Именно столько времени понадобилось учёным для создания теории всплесков, нашедшей плодотворные приложения. Теория продолжает интенсивно развиваться, в ней остаётся много нерешённых интересных задач.
Каждой непрерывной $2π$-периодической функции можно сопоставить проекцию на мир «всех» тригонометрических функций — её ряд Фурье:
$$ f\sim \frac{a_0}{2}+\sum\limits_{k=1}^\infty (a_k\cos kt + b_k\sin kt). $$
Значок «$\sim$» не отвечает ни за совпадение суммы ряда и функции, ни за саму возможность приписать бесконечной сумме, ряду, какое‐то значение (сходимость ряда). Частичная сумма
$$ (S_nf)(t)= \frac{a_0}{2}+\sum\limits_{k=1}^n (a_k\cos kt + b_k\sin kt), $$
полученная отбрасыванием «хвоста» ряда, совпадает с проекцией на подпространство $V_n$, является наилучшим приближением функции $f$ тригонометрическими многочленами степени $n$ (по норме $\|g\|=\sqrt{(g,g)}$).
В пространстве функций со скалярным произведением ряд Фурье сходится к функции ($\|f-S_nf\|\to 0$), т. е. набор коэффициентов Фурье — это полное, исчерпывающее представление функции.
Но необходимо отметить, что в пространстве функций есть и другие виды сходимости: поточечная, равномерная и т. д. Задача о сходимости ряда Фурье относительно этих видов сходимости тоже важна, она хорошо изучена.
Французский математик Жан-Батист Жозеф Фурье (Jean Baptiste Joseph Fourier, 1768—1830) в наполеоновскую эпоху был руководителем кафедры анализа и механики Политехнической школы в Париже (Ecole Polytechnique). Как было нередко в те времена, Фурье успешно совмещал научную работу с государственной деятельностью. И когда в 1798 году Наполеон решил завоевать Египет (Египетская экспедиция), то в состав экспедиционного корпуса были включены и учёные, члены Института (объединявшего научные академии Франции): Бертолле, Монж, Фурье. Да и сам Наполеон был членом Института по отделению физики и математики!
Из экспедиции Фурье привёз коллекцию древностей, которая впоследствии вдохновила Жана-Франсуа Шампольона на попытку (удавшуюся!) расшифровать египетские иероглифы.
Менее известно, что главное научное достижение самого Фурье — вывод уравнения теплопроводности и применение рядов Фурье для его решения — тоже связано с Египтом! Это уравнение для определения температуры точки физического тела в зависимости от времени.
Согласно легенде, необходимость вывода уравнения была стратегической: в экспедиции вино было необходимой частью рациона солдат, считалось, что оно помогает переносить климатические трудности. Задача формулировалась так: найти глубину винного погреба, в котором средняя температура была бы такой же, как в аналогичных сооружениях во Франции. Так появилось знаменитое уравнение теплопроводности, а поскольку колебания внешней температуры носят сезонный характер (с периодом 365 дней), то возникла счастливая догадка: раз температура — периодическая функция, то и искать решение надо с помощью уже известных периодических функций — тригонометрических.
Правдива ли эта легенда, доподлинно неизвестно. Главное, что Фурье представил свой метод 21 декабря 1807 года в докладе «О распространении тепла в твёрдом теле» на заседании Парижской Академии наук. Окончательное обоснование метод Фурье получил лишь в XX веке. По сей день он остаётся основным для решения уравнения теплопроводности на конечном временном интервале.
Протасов В. Ю. Синусоида и фрактал: элементы теории обработки сигналов и теории всплесков. — М.: МЦНМО, 2020.
Сэломон Д. Сжатие данных, изображений и звука. — М.: Техносфера, 2004. — [Инженерный взгляд на теорию всплесков, приводятся стандарты сжатия данных].
Добеши И. Десять лекций по вейвлетам. — Ижевск: РХД, 2001. — [Для студентов — учебник от одного из первопроходцев теории всплесков].
Араго Д. Ф. Биографии знаменитых астрономов, физиков и геометров: В 3 т. — СПб., 1859—1861.