‍Обработка сигналов: от волн к всплескам

Каж­дый раз, когда мы рабо­таем на компью­тере или гово­рим по мобиль­ному теле­фону, запус­каются мощ­ные меха­низмы обра­ботки, хра­не­ния и пере­дачи сиг­на­лов. Эти меха­низмы осно­ваны на достиже­ниях тео­рии функций, опти­ми­за­ции, тео­рии алго­ритмов и ещё десятка обла­стей современ­ной матема­тики. Одни из них роди­лись ещё в поза­прошлом веке, другие (и их большин­ство) — прак­ти­че­ски вчера. Тео­рия обра­ботки сиг­на­лов явля­ется одним из наи­бо­лее вос­тре­бо­ван­ных прак­ти­кой раз­де­лов сего­дняш­ней матема­тики.

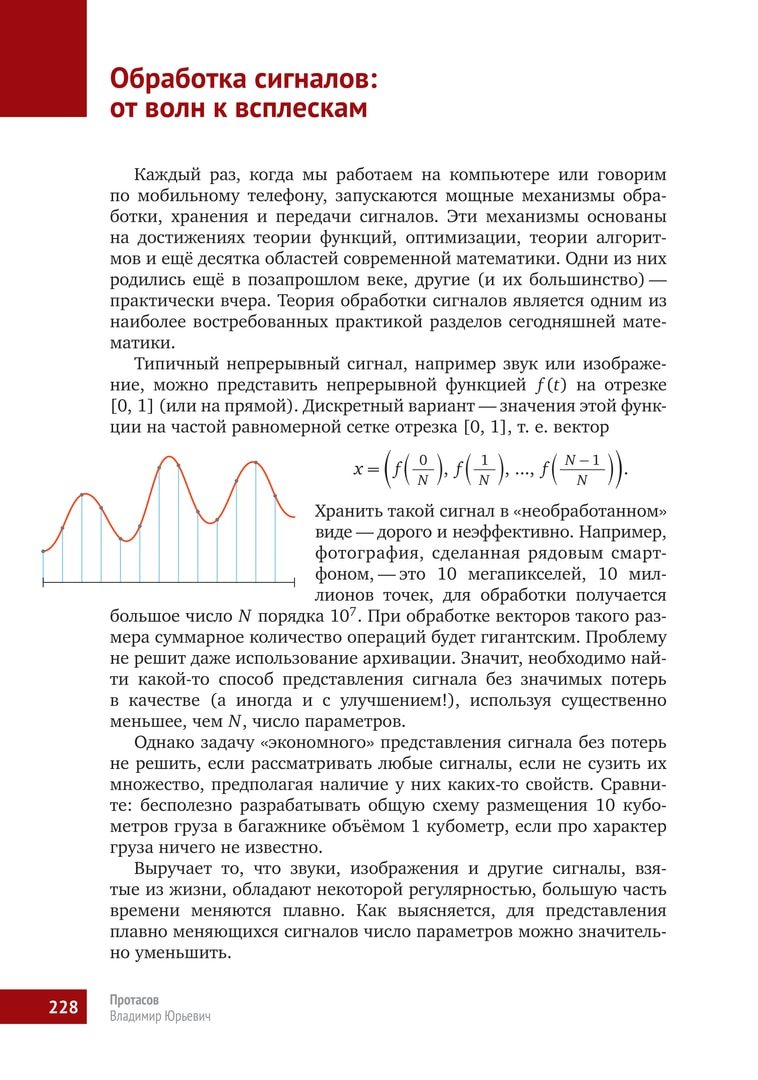
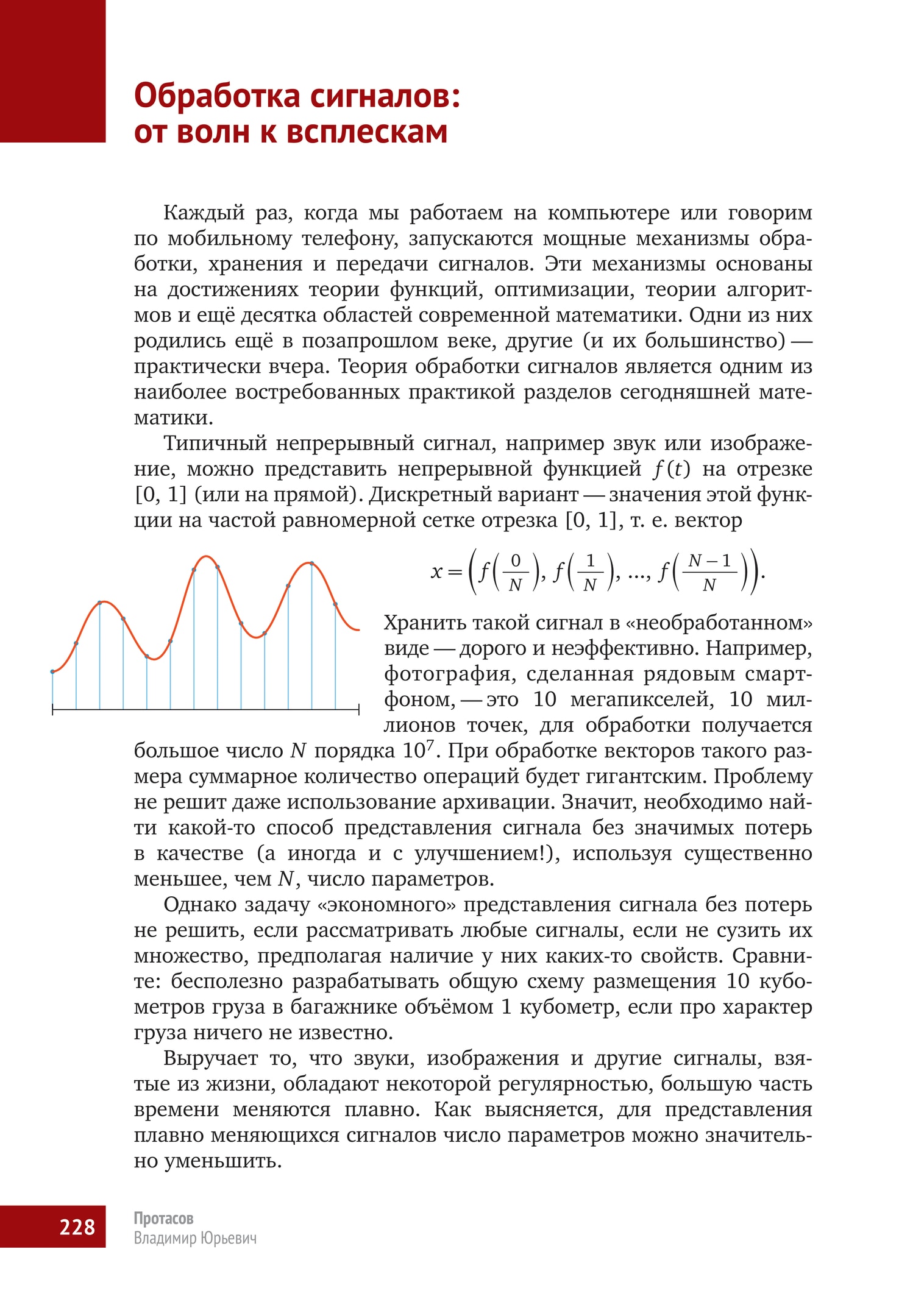
Типич­ный непре­рыв­ный сиг­нал, напри­мер звук или изоб­раже­ние, можно пред­ста­вить непре­рыв­ной функцией $f(t)$ на отрезке $[0,1]$ (или на прямой). Дис­крет­ный вари­ант — зна­че­ния этой функции на частой рав­но­мер­ной сетке отрезка $[0,1]$, т. е. век­тор $$ x={ \left( f{ \left( \frac 0N \right)},f{ \left( \frac 1N\right)},…,f{ \left(\frac { N-1 }N \right ) }\right)}. $$

Хра­нить такой сиг­нал в «необ­ра­бо­тан­ном» виде — дорого и неэффек­тивно. Напри­мер, фотография, сде­лан­ная рядо­вым смарт­фо­ном, — это 10 мегапик­се­лей, 10 мил­ли­о­нов точек, для обра­ботки полу­ча­ется большое число $N$ порядка $10^7$. При обра­ботке век­то­ров такого размера суммар­ное коли­че­ство опе­раций будет гигант­ским. Про­блему не решит даже исполь­зо­ва­ние архи­вации. Зна­чит, необ­хо­димо найти какой‐то спо­соб пред­став­ле­ния сиг­нала без зна­чимых потерь в каче­стве (а иногда и с улучше­нием!), исполь­зуя суще­ственно меньшее, чем $N$, число парамет­ров.

Однако задачу «эко­ном­ного» пред­став­ле­ния сиг­нала без потерь не решить, если рас­смат­ри­вать любые сиг­налы, если не сузить их множе­ство, предпо­лагая нали­чие у них каких-то свойств. Срав­ните: бес­по­лезно раз­ра­ба­ты­вать общую схему размеще­ния 10 кубомет­ров груза в багаж­нике объёмом 1 кубометр, если про харак­тер груза ничего не известно.

Выру­чает то, что звуки, изоб­раже­ния и другие сиг­налы, взя­тые из жизни, обла­дают неко­то­рой регу­ляр­но­стью, большую часть времени меняются плавно. Как выяс­ня­ется, для пред­став­ле­ния плавно меняющихся сиг­на­лов число парамет­ров можно зна­чи­тельно уменьшить.

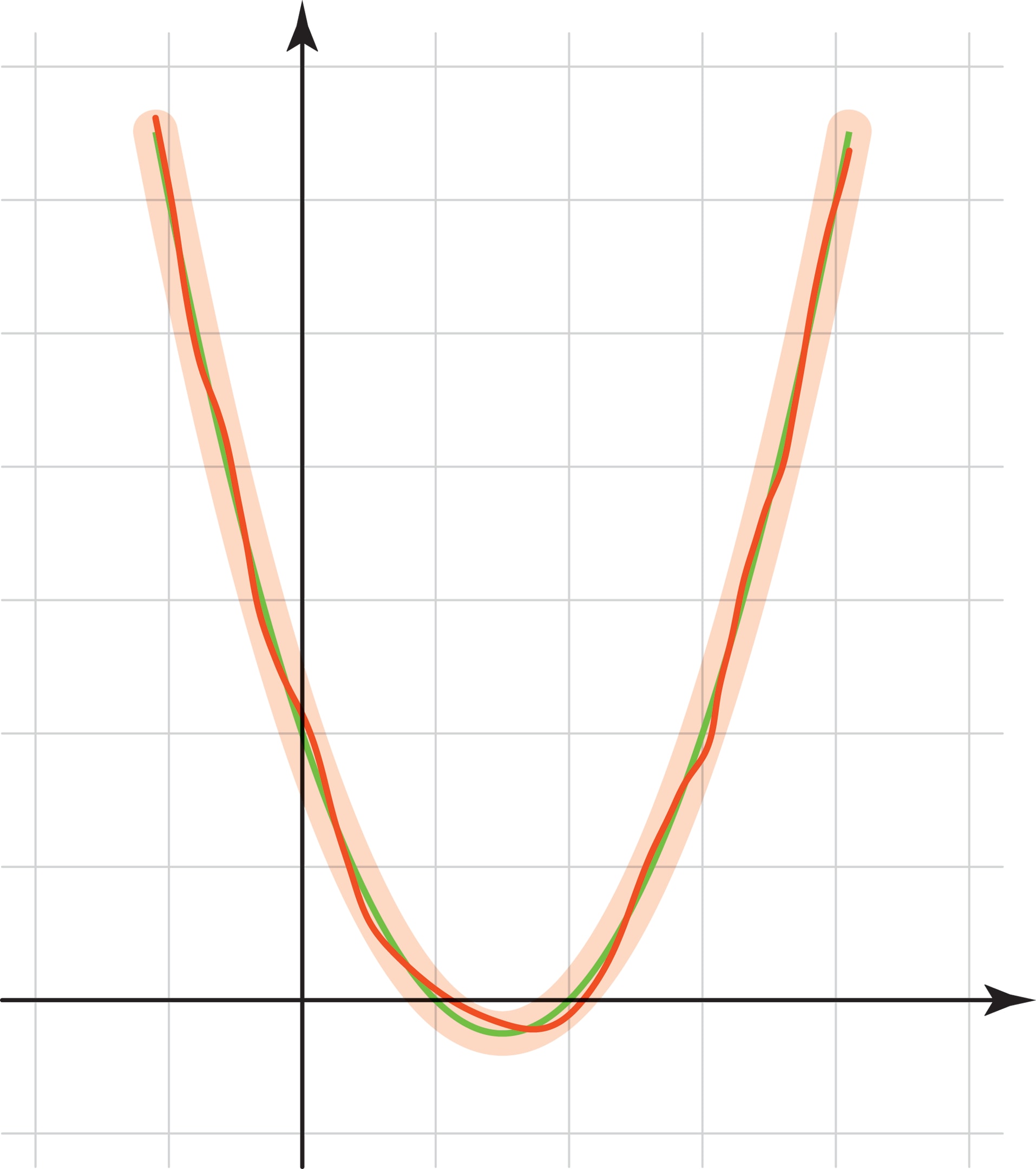
Тео­рия при­ближе­ния функций. Основ­ная идея тео­рии при­ближе­ний — заме­нить «слож­ную» функцию $f(t)$ близ­кой к ней более про­стой функцией, являющейся линей­ной ком­би­нацией выбран­ных зара­нее «базис­ных» функций. (Линей­ной ком­би­нацией назы­ва­ется конеч­ная сумма слага­емых, каж­дое из кото­рых — одна из базис­ных функций, умножен­ная на какое-то число. Сам базис­ный набор может быть и бес­ко­неч­ным.) Если удастся найти при­ближе­ние с точ­но­стью, необ­хо­димой для прак­ти­че­ских нужд, то можно пере­да­вать не гигант­ский набор зна­че­ний $f(t)$ в $N$ точ­ках, а скром­ный по чис­лен­но­сти набор коэффици­ен­тов при базис­ных элемен­тах в при­ближе­нии. По полу­чен­ному набору коэффици­ен­тов функция может быть вос­ста­нов­лена с выбран­ной точ­но­стью.

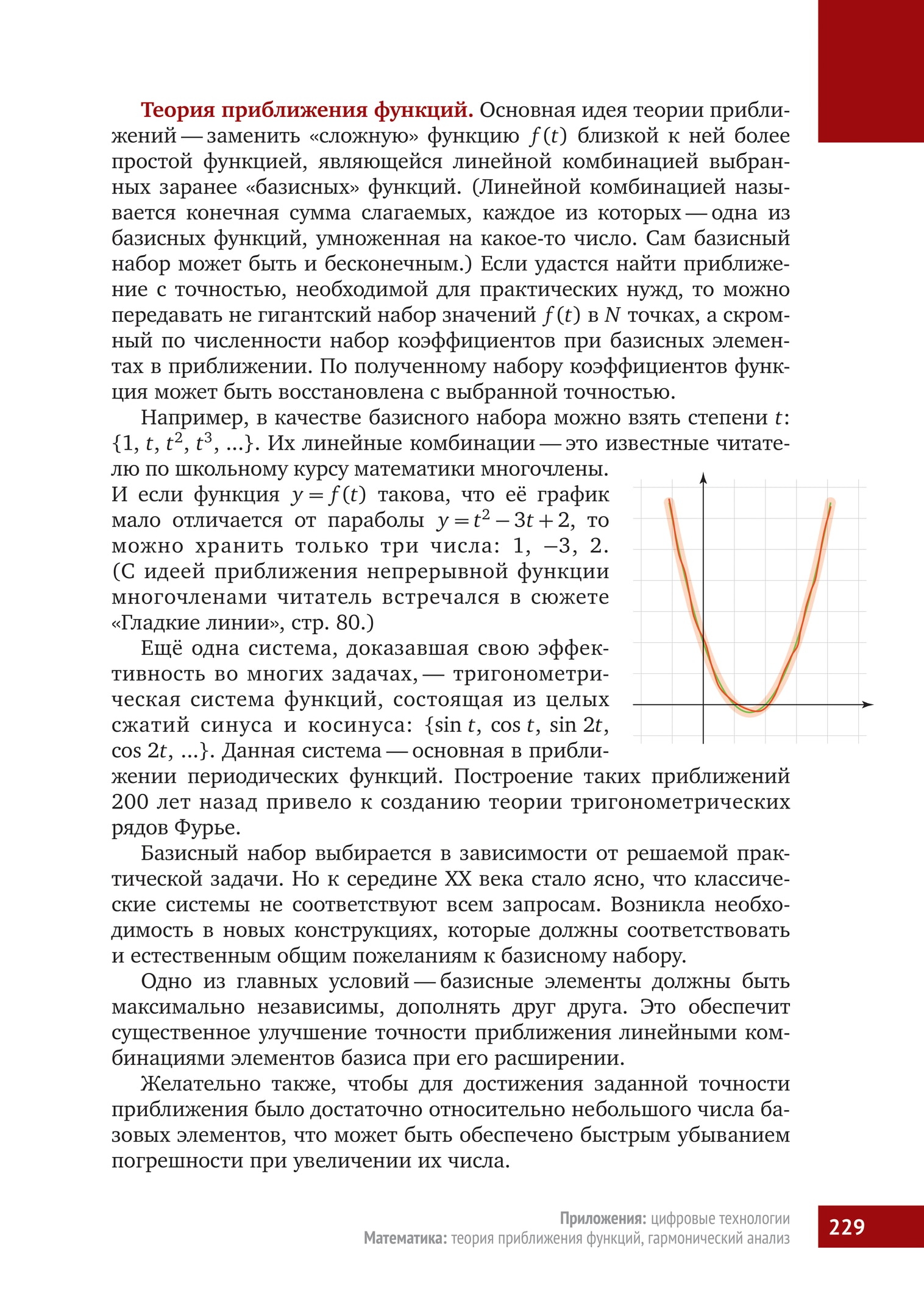
Напри­мер, в каче­стве базис­ного набора можно взять степени $t$: $\{1, t, t^2, t^3, …\}$. Их линей­ные ком­би­нации — это извест­ные чита­телю по школь­ному курсу матема­тики много­члены. И если функция $y=f(t)$ такова, что её график мало отли­ча­ется от пара­болы $y=t^2-3t+2$, то можно хра­нить только три числа: 1, -3, 2. (С идеей при­ближе­ния непре­рыв­ной функции много­чле­нами чита­тель встре­чался в сюжете ⁠«Глад­кие линии».)

Ещё одна система, дока­завшая свою эффек­тив­ность во многих зада­чах, — триго­номет­ри­че­ская система функций, состо­ящая из целых сжа­тий синуса и коси­нуса: $\{\sin t$, $\cos t$, $\sin 2t$, $\cos 2t$, $… \}$. Дан­ная система — основ­ная в при­ближе­нии пери­о­ди­че­ских функций. Постро­е­ние таких при­ближе­ний 200 лет назад при­вело к созда­нию тео­рии триго­номет­ри­че­ских рядов Фурье.

Базис­ный набор выби­ра­ется в зави­симо­сти от реша­емой прак­ти­че­ской задачи. Но к сере­дине XX века стало ясно, что клас­си­че­ские системы не соот­вет­ствуют всем запро­сам. Воз­никла необ­хо­димость в новых кон­струкциях, кото­рые должны соот­вет­ство­вать и есте­ствен­ным общим поже­ла­ниям к базис­ному набору.

Одно из глав­ных усло­вий — базис­ные элементы должны быть мак­симально неза­ви­симы, допол­нять друг друга. Это обес­пе­чит суще­ствен­ное улучше­ние точ­но­сти при­ближе­ния линей­ными ком­би­наци­ями элемен­тов базиса при его расши­ре­нии.

Жела­тельно также, чтобы для достиже­ния задан­ной точ­но­сти при­ближе­ния было доста­точно отно­си­тельно небольшого числа базо­вых элемен­тов, что может быть обес­пе­чено быст­рым убы­ва­нием погреш­но­сти при уве­ли­че­нии их числа.

Ещё одно поже­ла­ние к базо­вым элемен­там носит вычис­ли­тель­ный харак­тер. Важно, чтобы нахож­де­ние коэффици­ен­тов хорошего при­ближе­ния было неслож­ной и быстро реша­емой зада­чей.

Одна из эффек­тив­ных идей, воз­никших в матема­тике в начале XX века, — изу­чать возмож­ность при­ближе­ния не отдель­ных функций, а целых клас­сов функций, обла­дающих общими свойствами, напри­мер, оди­на­ко­вых в смысле глад­ко­сти.

Геомет­ри­че­ский взгляд. При­ближе­ния в выде­лен­ных клас­сах непре­рыв­ных и дис­крет­ных сиг­на­лов настолько похожи, что изу­че­ние принци­пов и мето­дов будет вестись пооче­рёдно, в зави­симо­сти от степени нагляд­но­сти в том или ином слу­чае.

Начать разго­вор проще с дис­крет­ного слу­чая: век­тор $x$ — не про­сто набор чисел, это точка геомет­ри­че­ского про­стран­ства $\mathbb R^N$, кото­рое можно пред­став­лять по ана­логии с при­выч­ным трёхмер­ным про­стран­ством $\mathbb R^3$ с обыч­ной евкли­до­вой геомет­рией. Напом­ним, что в прак­ти­че­ских зада­чах размер­ность $\mathbb R^N$ — гигант­ская (напри­мер, $N\sim 10^7$).

Для дис­крет­ного сиг­нала на сетке с шагом $1/N$ изме­не­ние коор­ди­нат век­тора будет плав­ным (глад­ким), если модуль раз­но­сти двух сосед­них коор­ди­нат не пре­вос­хо­дит $1/N$. И доля таких сиг­на­лов среди всех будет весьма небольшой. Все $N$‐мер­ные век­торы, коор­ди­наты кото­рых неот­рица­тельны и не пре­вос­хо­дят еди­ницы, обра­зуют куб еди­нич­ного объёма ($N$‐мер­ного). Среди них глад­кие сиг­налы запол­няют $N$‐мер­ный парал­ле­лепипед, его объём весьма мал и равен $(2/N)^{N-1}$. Нагляд­ное пред­став­ле­ние — смарт­фон (прямо­уголь­ный, тон­кий, почти плос­кий), лежащий на дне коробки куби­че­ской формы. Чтобы оце­нить долю глад­ких сиг­на­лов среди всех, рас­смот­рим модель­ный при­мер с фотографией, сде­лан­ной на смарт­фон: при $N=10^7$ объём парал­ле­лепипеда невозможно пред­ста­вить, он меньше, чем $1/10^{6  000  000}$.

Итак, глад­кие сиг­налы — мизер­ная часть множе­ства про­из­воль­ных сиг­на­лов. Опи­са­ние всех глад­ких сиг­на­лов можно сде­лать доста­точно «крат­ким», занимающим меньше памяти. Тех­ни­че­ски это озна­чает, что можно найти базо­вые сиг­налы, число кото­рых зна­чи­тельно меньше чем $N$, но линей­ными ком­би­наци­ями кото­рых («плос­ко­стью», зада­ва­емой ими) можно при­бли­зить с доста­точ­ной точ­но­стью выбран­ный плав­ный сиг­нал (вспом­ните дно коробки как плос­кость, в кото­рой най­дётся под­хо­дящее при­ближе­ние для любой точки смарт­фона). Более общий слу­чай: выпук­лое тело малого объёма в $\mathbb R^N$ можно при­бли­зить плос­ко­стью, размер­ность кото­рой меньше, чем $N$; при­чём чем меньше объём, тем лучше при­ближе­ние (при фик­си­ро­ван­ной размер­но­сти плос­ко­сти). При­бли­зить — озна­чает про­ве­сти плос­кость так, чтобы она про­хо­дила рядом с каж­дой точ­кой выпук­лого тела, т. е. чтобы рас­сто­я­ние от каж­дой точки тела до плос­ко­сти было мало.

Для реа­ли­за­ции идеи оста­ётся выбрать базис сиг­на­лов, кото­рый порож­дает плос­кость, хорошо при­ближающую дан­ное выпук­лое тело глад­ких сиг­на­лов.

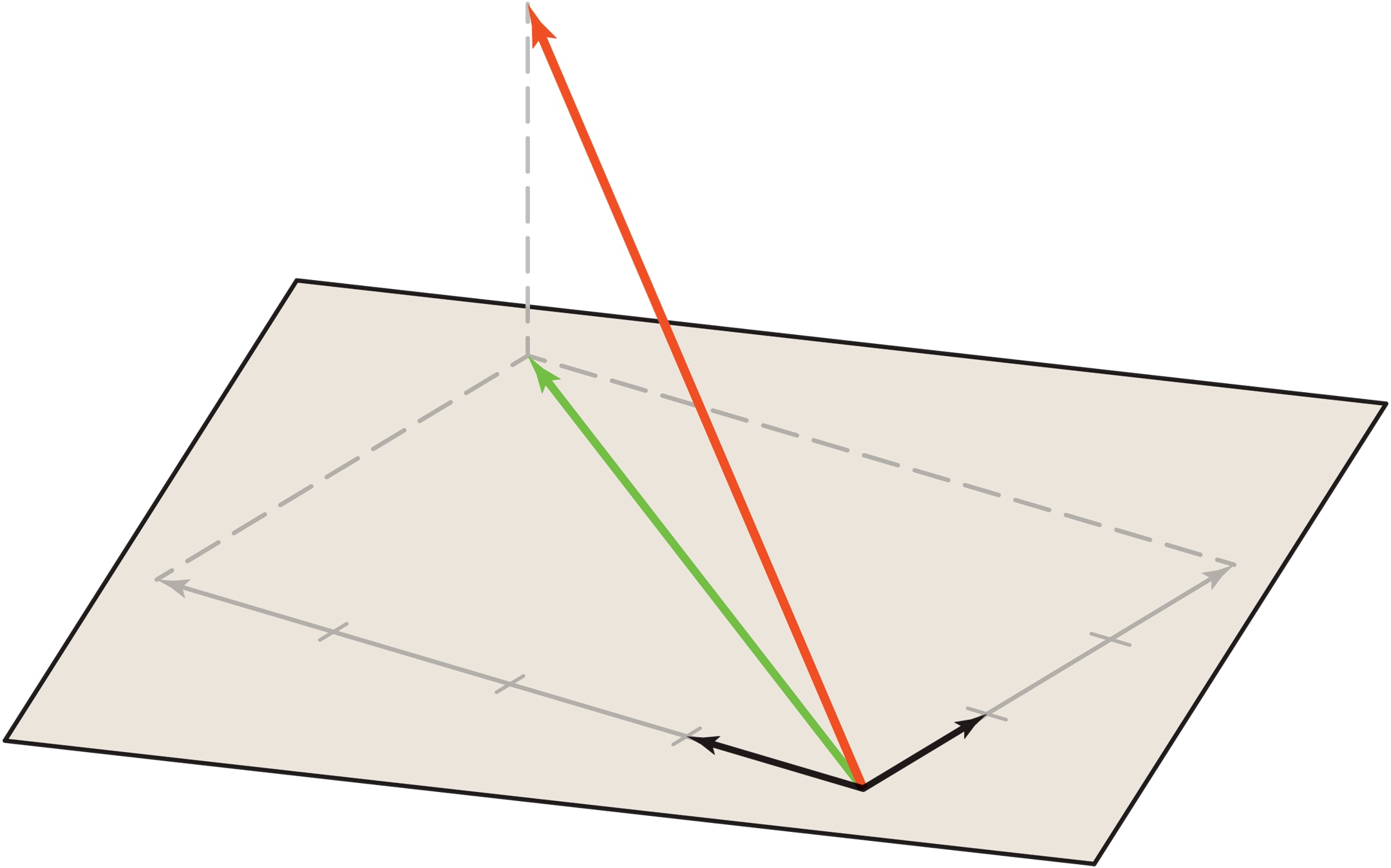
Работа в $\mathbb R^N$ с этим бази­сом будет зна­чи­тельно удоб­нее, если все базис­ные век­торы $\{e_k\}$ будут попарно ортого­нальны (перпен­ди­ку­лярны) и норми­ро­ваны (еди­нич­ной длины): ска­ляр­ные про­из­ве­де­ния $(e_i,e_j)=0$, если $i\ne j$, и $(e_i,e_i)=1$ при любом $i$. В этом слу­чае отыс­ка­ние наи­лучшего при­ближающего элемента «авто­ма­ти­зи­ру­ется». Во‐пер­вых, это про­екция век­тора на плос­кость. Во‐в­то­рых, про­екция равна $\sum \mathord(x, e_k)  e_k$, т. е. коэффици­енты при таком раз­ложе­нии при­ближающего элемента по базису  — ска­ляр­ные про­из­ве­де­ния век­тора $x$ и базис­ных век­то­ров $e_k$.

Про­стран­ства глад­ких функций. В этом раз­деле есть «страш­ные» формулы, но «начи­нающий» матема­тик может воспри­нимать их как иллю­страции.

Для непре­рыв­ных сиг­на­лов глад­кость — мера плав­но­сти изме­не­ния функции. Про­стой непре­рыв­но­сти на прак­тике недо­ста­точно, разумно-минималь­ная степень глад­ко­сти — свойство липшице­во­сти функции (кото­рое уже встре­ча­лось в дис­крет­ном слу­чае). Предпо­лага­ется, что рас­сто­я­ние между двумя точ­ками не может уве­ли­читься больше, чем в задан­ное число раз, т. е. най­дётся такое число $L$, что при любых $t_1$ и $t_2$ выпол­ня­ется нера­вен­ство $$|f(t_1)-f(t_2)|\le L|t_1-t_2|.$$

Можно счи­тать, что $L$ — харак­те­ри­стика рас­тяже­ния рези­но­вой нити на отрезке $[0,1]$, с помощью кото­рой «изго­то­вили» график функции $f(t)$. Липшице­вость — суще­ствен­ное уси­ле­ние про­стой непре­рыв­но­сти, но более сла­бое свойство, чем непре­рыв­ность про­из­вод­ной $f'(t)$ во всех точ­ках.

В про­стран­стве непре­рыв­ных функций $C[a,b]$ есте­ствен­ное поня­тие рас­сто­я­ния между функци­ями $f$ и $g$ свя­зано с бли­зо­стью их графи­ков во всех точ­ках: $$ d(f,g)=\max\limits_{t\in [a,b]} |f(t)-g(t)|.$$

Рас­сто­я­ние от $f$ до нуле­вой функции назы­ва­ется нормой: $$ \|f\|=\max\limits_t |f(t)|, $$

сле­до­ва­тельно, $$d(f,g)=\|f-g\|.$$

(Это рас­сто­я­ние назы­вают иногда чебышёв­ским, в честь Паф­ну­тия Льво­вича Чебышева — осно­вопо­лож­ника тео­рии при­ближе­ния функций.) Это рас­сто­я­ние можно исполь­зо­вать и в клас­сах $C^r[a,b]$, состо­ящих из $r$ раз диффе­ренци­ру­емых функций, у кото­рых старшая про­из­вод­ная $f^{(r)}(t)$ непре­рывна на отрезке $[a,b]$. Вве­дён­ное поня­тие рас­сто­я­ния поз­во­ляет оце­нить достижимую точ­ность при­ближе­ния в зави­симо­сти от глад­ко­сти функции.

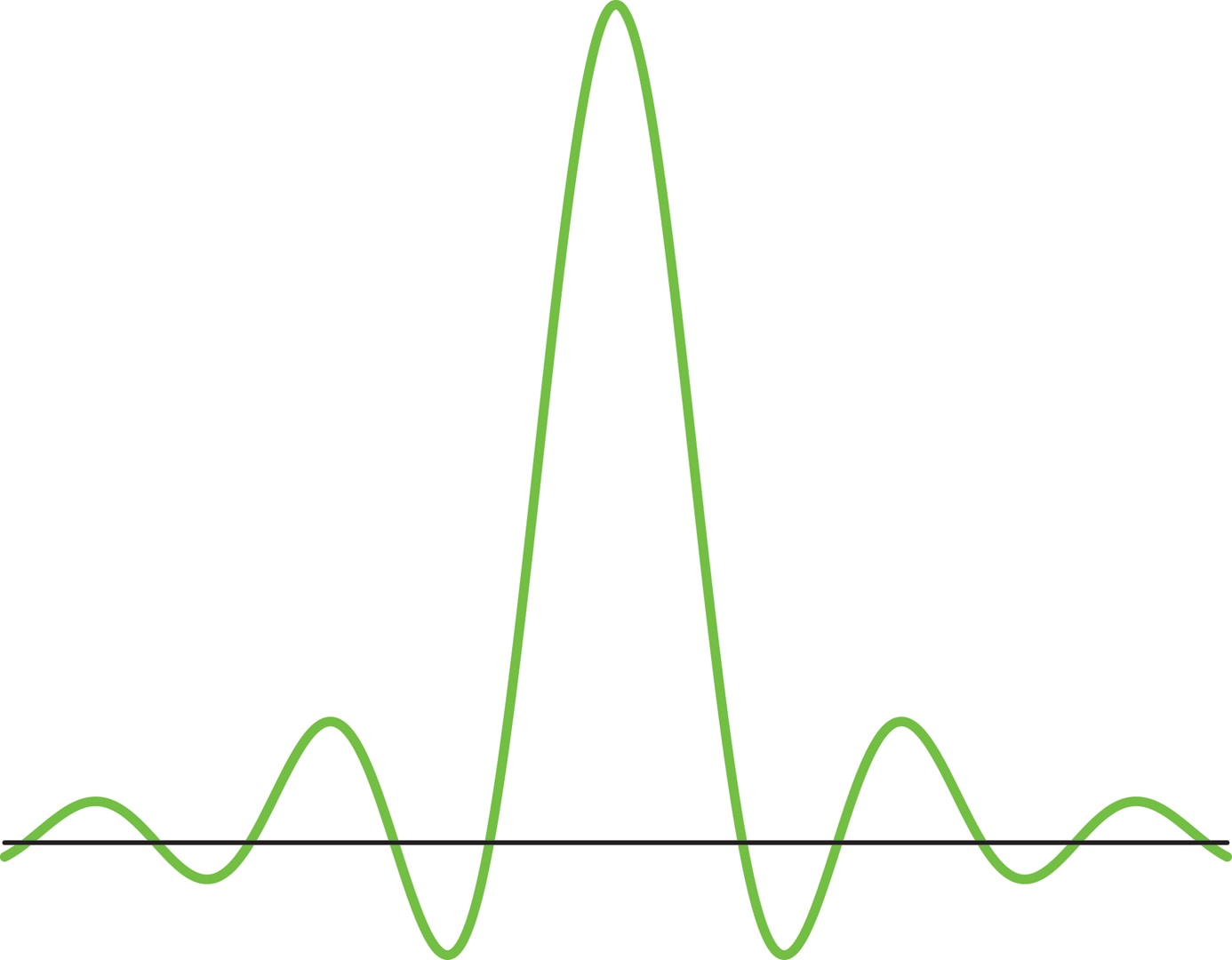
Напри­мер, можно утвер­ждать (тео­рема Джек­сона), что для $2π$-пери­о­ди­че­ской функции $f\in C^r[0,2π]$ най­дётся триго­номет­ри­че­ский много­член $f_n$ степени $n$ (элемент плос­ко­сти, порож­дён­ной функци­ями $\cos kt$ и $\sin kt$ при $k=0$, 1, …, $n$), рас­сто­я­ние от кото­рого до $f$, т. е. $||f-f_n||$, имеет поря­док $1/n^r$.

Мы уже гово­рили о том, что в $\mathbb R^N$ можно вве­сти ска­ляр­ное про­из­ве­де­ние и сде­лать его похожим по устройству на $\mathbb R^3$. Но можно раз­вить эту геомет­ри­че­скую идею и вве­сти бес­ко­неч­номер­ные про­стран­ства со ска­ляр­ным про­из­ве­де­нием. Пожа­луй, самый важ­ный при­мер — это класс функций на отрезке $[a,b]$ (доста­точно широ­кий, напри­мер, в него вхо­дят все непре­рыв­ные функции), на этом классе ска­ляр­ное про­из­ве­де­ние и норма функции (длина элемента) опре­де­ляются форму­лами $$ \textstyle (f,g)=\int\limits_a^b f(t)  g(t)  dt, \qquad \|f\|=\sqrt{(f,f)}. $$

В результате мир функций ста­но­вится геомет­ри­че­ским, в нём можно изме­рять рас­сто­я­ния и углы между функци­ями. Напри­мер, угол между $f(t)=t$ и $g(t)=2t$ равен нулю, эти век­торы сонаправ­лены. Вклю­че­ние в базис­ный набор подоб­ных функций, дуб­ли­рующих друг друга, бес­смыс­ленно. А если равно нулю ска­ляр­ное про­из­ве­де­ние функций, то функции назы­ваются ортого­наль­ными, они направ­лены в раз­ные сто­роны, допол­няют друг друга. Ока­зы­ва­ется, что все функции из множе­ства $\{1, \sin t, \cos t, \sin 2t, \cos2t, …\}$ попарно ортого­нальны на $[0,2π]$. В тео­рии при­ближе­ний появ­ле­ние ортого­наль­ного набора элемен­тов — знак каче­ства, оптималь­но­сти, совершен­ства системы.

В про­стран­стве функций со ска­ляр­ным про­из­ве­де­нием рабо­тают те же методы при­ближе­ния (про­екции), что и в $\mathbb R^N$.

Метод Фурье. Стан­дарт­ный базис — ортого­наль­ная и норми­ро­ван­ная (орто­норми­ро­ван­ная) система функций $\{e_j\}_{j\ge 0}$: $$ e_0=\frac{1}{\sqrt{2π}}, \quad e_{2k-1}=\frac{1}{\sqrt{\vphantom2π}} \cos kt, \quad e_{2k}=\frac{1}{\sqrt{\vphantom2π}} \sin kt. $$

Плос­кость $V_n$, порож­да­емая функци­ями $\{e_0, e_1, …, e_{2n}\}$, состоит из триго­номет­ри­че­ских много­чле­нов степени $n$, т. е. функций вида $\sum\limits_{k=0}^n \mathord(a_k\cos kx + b_k \sin kx)$. Подпро­стран­ства $V_n$ расши­ряются с ростом $n$ и в неко­то­ром смысле исчерпы­вают всё про­стран­ство функций. Точ­нее, для любой функции из этого про­стран­ства можно найти её при­ближе­ние из неко­то­рого $V_n$ с задан­ной точ­но­стью. Наи­лучшее при­ближе­ние из $V_n$ — это про­екция $f$ на эту плос­кость $$ S_n f=\sum\limits_{k=0}^{2n} \mathord(f, e_k)  e_k. $$

Как и в $\mathbb R^N$, спо­соб нахож­де­ния коэффици­ен­тов в раз­ложе­нии про­екции — уни­вер­саль­ный, это вычис­ле­ние ска­ляр­ных про­из­ве­де­ний $(f, e_k)$.

В про­стран­стве функций орто­норми­ро­ван­ная система $\{e_k\}_{k\ge 0}$ играет важ­ную роль, триго­номет­ри­че­скими много­чле­нами успешно при­ближаются глад­кие функции (выпук­лое множе­ство в про­стран­стве функций). Напри­мер, для функции $f$ класса $C^r[0,2π]$ с помощью тео­ремы Джек­сона несложно уста­но­вить, что погреш­ность $\|f-S_nf\|$ имеет поря­док $1/n^r$.

Тео­рема Джек­сона поз­во­ляет оце­нить число коэффици­ен­тов, кото­рые нужно сохра­нить вме­сто ориги­наль­ного сиг­нала, чтобы обес­пе­чить необ­хо­димую точ­ность. Это число гораздо меньше, чем коли­че­ство зна­че­ний на сетке. И чем выше глад­кость сиг­нала, тем меньше пона­до­бится для него коэффици­ен­тов. Напри­мер, если точ­ность при­ближе­ния $\varepsilon=0{,}01$, то при $r=1$ (что соот­вет­ствует часто встре­чающимся липшице­вым сиг­на­лам) такую погреш­ность обес­пе­чи­вает 201 коэффици­ент. А если $r=3$ (такие сиг­налы встре­чаются гораздо реже) вся «посылка» будет состо­ять из 11 чисел!

Если функция и при­ближающий её триго­номет­ри­че­ский много­член отли­чаются мало, то номера вхо­дящих в него гар­мо­ник (сину­сов и коси­ну­сов) опре­де­ляют спектр частот, из кото­рых в действи­тель­но­сти состав­лен сиг­нал. А коэффици­енты в много­члене гово­рят о вкладе, кото­рый вно­сят соот­вет­ствующие гар­мо­ники. Нагляд­ный при­мер: тембр звука скла­ды­ва­ется из сину­со­и­даль­ных коле­ба­ний струны, коэффици­енты в раз­ложе­нии — ампли­туды, гром­кость (см. ⁠«Чистые интер­валы»).

Дис­крет­ное пре­об­ра­зо­ва­ние Фурье. Идею замены непре­рыв­ного сиг­нала $N$-мер­ным век­то­ром, компо­ненты кото­рого — зна­че­ния функции на сетке с шагом $1/N$, можно при­ме­нить и к базис­ным набо­рам, напри­мер к триго­номет­ри­че­ским функциям. Свойства триго­номет­ри­че­ской системы — орто­норми­ро­ван­ность и «базис­ные» спо­соб­но­сти — сохра­няются и в «дис­крет­ном» вари­анте: полу­ча­ется орто­норми­ро­ван­ная система $\{E_k\}$ из $N$ век­то­ров в $\mathbb R^N$. (Тех­ни­че­ское изяще­ство кон­струкции достига­ется заме­ной каж­дой пары $\{\cos kt, \sin kt\}$ двумя экс­по­нен­тами $e^{\pm ikt}$; основа этой опе­рации — формула Эйлера $e^{it}=\cos t + i\sin t$.)

Коэффици­енты в раз­ложе­нии дис­крет­ного сиг­нала $x$ (век­тора из $\mathbb R^N$) по базису $\{E_k\}$ обра­зуют $N$-мер­ный век­тор $\widehat x$, кото­рый назы­вают дис­крет­ным пре­об­ра­зо­ва­нием Фурье. На этом шаге эко­номии нет: про­сто один $N$‐мер­ный век­тор пре­вра­тили в дру­гой.

Но если $x$ — сиг­нал глад­кий, то коор­ди­наты век­тора $\widehat x$ с большими номе­рами малы. Отбро­сив их (т. е. заме­нив нулями, кото­рые не нужно пере­да­вать), можно полу­чить хорошее, но «корот­кое» при­ближе­ние для век­тора $\widehat x$. При­ме­нив обрат­ное дис­крет­ное пре­об­ра­зо­ва­ние Фурье к этому при­ближе­нию, полу­чим век­тор, хорошо при­ближающий сиг­нал $x$. Это осно­вано на двух свойствах базиса $\{E_k\}$, уна­сле­до­ван­ных от непре­рыв­ного базиса $\{e_k\}$. Во‐пер­вых, обрат­ное пре­об­ра­зо­ва­ние Фурье вычис­ля­ется по тем же форму­лам, что и прямое (един­ствен­ное изме­не­ние — замена зна­ков в пока­за­теле экс­по­нент). Во‐в­то­рых, дис­крет­ное пре­об­ра­зо­ва­ние Фурье — движе­ние евкли­дова про­стран­ства $\mathbb R^N$, при кото­ром сохра­няются ска­ляр­ные про­из­ве­де­ния $(\widehat x, \widehat y)=(x,y)$, а сле­до­ва­тельно, и длины, и углы, и погреш­но­сти при­ближе­ния.

Для оценки точ­но­сти при­ближе­ния сиг­нала с помощью дис­крет­ного пре­об­ра­зо­ва­ния Фурье можно восполь­зо­ваться дис­крет­ной вер­сией тео­ремы Джек­сона. Ока­зы­ва­ется, при $N=10^7$ и задан­ной точ­но­сти $\varepsilon=0{,}01$ для слу­чая $r=1$ (липшицевы сиг­налы) при­дётся вычис­лить при­мерно $6\cdot 10^5$ коэффици­ен­тов Фурье, а для $r=3$ — при­мерно 140.

Типич­ное сжа­тие по методу Фурье — при­мерно в 10—20 раз (число $N=10^7$ заме­ня­ется на $6\cdot 10^5$). Но чтобы этот выиг­рыш полу­чить, при­дётся вычис­лять десятки тысяч коэффици­ен­тов Фурье, а это озна­чает выпол­не­ние $2N^2$ арифме­ти­че­ских опе­раций.

Напри­мер, при $N=10^7$ полу­ча­ется «нере­аль­ное» зна­че­ние $2\cdot 10^{14}$. Отправка фотографии, сде­лан­ной смарт­фо­ном, заняла бы… более полу­часа! А ведь потом ещё при­дётся потра­тить столько же времени на рас­ко­ди­ровку, т. е. на обрат­ное пре­об­ра­зо­ва­ние Фурье. Конечно, нам нужны не все коэффици­енты Фурье, при глад­ком сиг­нале их число уменьша­ется, но и тогда объём вычис­ле­ний полу­ча­ется недопу­стимо большим.

Неужели из этой ситу­ации нет ника­кого выхода? Ока­зы­ва­ется, суще­ствует спе­ци­аль­ный алго­ритм, кото­рый даёт возмож­ность нахо­дить коэффици­енты Фурье не по отдель­но­сти (один за другим), а парал­лельно. Это — быст­рое пре­об­ра­зо­ва­ние Фурье, в кото­ром вычис­ле­ния устро­ены так, что их результаты исполь­зуются для опре­де­ле­ния сразу нескольких коэффици­ен­тов Фурье (ана­логия — быст­рое умноже­ние, см. ⁠«Быст­рая арифме­тика». Эко­номия полу­ча­ется суще­ствен­ной: число опе­раций сокраща­ется с $2N^2$ до $2N\log_2 N$. Напри­мер, при $N=10^7$ необ­хо­димо выпол­нить не $2\cdot 10^{14}$ опе­раций, а менее $5\cdot 10^8$ — выиг­рыш в $400 000$ раз! Отправка фотографии займёт долю секунды!

Вывод, кото­рый необ­хо­димо сде­лать, такой: при постро­е­нии при­ближе­ния надо учи­ты­вать не только коли­че­ство исполь­зу­емых коэффици­ен­тов Фурье, но и число опе­раций при их вычис­ле­нии. Заме­тим, что в задаче раз­ложе­ния по базису из $N$ элемен­тов число опе­раций (слож­ность, см. ⁠«Тео­рия слож­но­сти») не может быть меньше чем $N$. Действи­тельно, для опре­де­ле­ния каж­дого коэффици­ента нужна хотя бы одна опе­рация. Слож­ность метода быст­рого пре­об­ра­зо­ва­ния Фурье явля­ется почти линей­ной, т. е. близка к гра­ни­цам возмож­ного.

Недо­ста­ток триго­номет­ри­че­ской системы. Выбор триго­номет­ри­че­ских функций в каче­стве базис­ных для обра­ботки глад­ких сиг­на­лов уда­чен во многих отноше­ниях, от эффек­тив­но­сти до удоб­ства. Эффек­тив­ность — высо­кий коэффици­ент сжа­тия — обес­пе­чи­ва­ется глад­ко­стью триго­номет­ри­че­ских функций и тео­ремой Джек­сона. Удоб­ство свя­зано и с общим свойством ортого­наль­ной системы — наи­лучшим при­ближе­нием явля­ется про­екция, и с тем, что коэффици­енты раз­ложе­ния в про­екции можно найти с помощью быст­рого пре­об­ра­зо­ва­ния Фурье (вычис­ли­тель­ная слож­ность близка к линей­ной). В целом метод Фурье хорош и широко при­ме­ня­ется.

Но у триго­номет­ри­че­ской системы есть серьёз­ный и неустра­нимый недо­ста­ток, кото­рый стал осо­бенно заме­тен при исполь­зо­ва­нии мощ­ных компью­те­ров, — чув­стви­тель­ность к шуму.

Шум — искаже­ние сиг­нала, ошибка. Как пра­вило, это крат­ко­времен­ная, но большая по вели­чине добавка к основ­ному сиг­налу. Напри­мер: щел­чок, треск — на пла­стинке, пылинка — на фотографии. Для дис­крет­ного сиг­нала $x$ шум — это изме­не­ние одной из его коор­ди­нат. Но в раз­ложе­нии Фурье сиг­нала $x$ изме­нятся все коор­ди­наты век­тора $\widehat x$ (на одну и ту же вели­чину) — ошибка в одной коор­ди­нате разма­за­лась рав­но­мерно по всем коор­ди­на­там $\widehat x$, замас­ки­ро­ва­лась. Поэтому найти место повре­жде­ния сиг­нала и испра­вить ошибку будет трудно. В результате при обра­ботке мето­дом Фурье зашум­лён­ной фотографии полу­чится менее чёт­кое, размытое изоб­раже­ние.

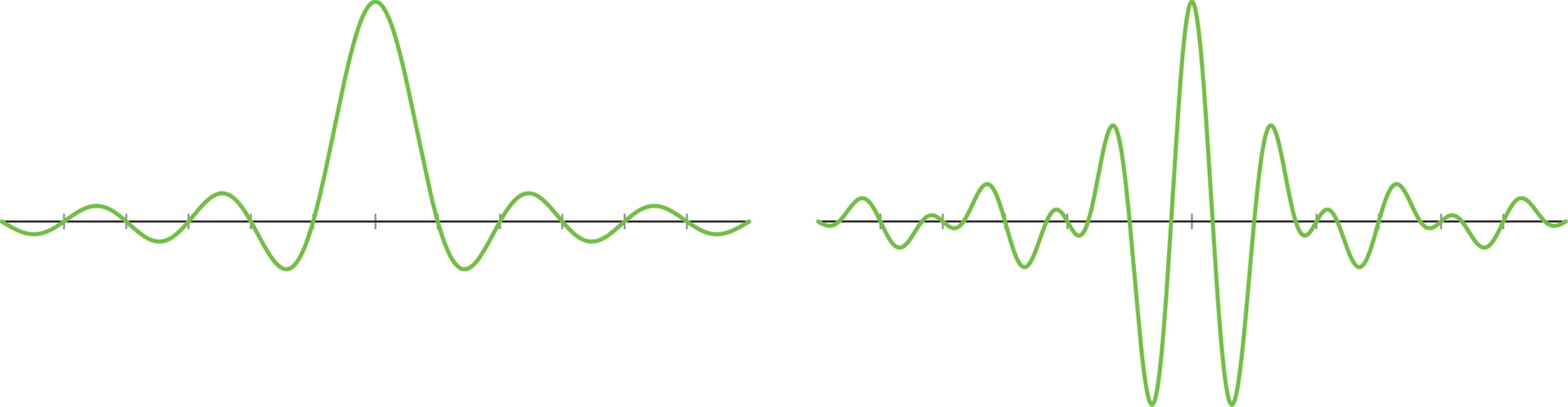
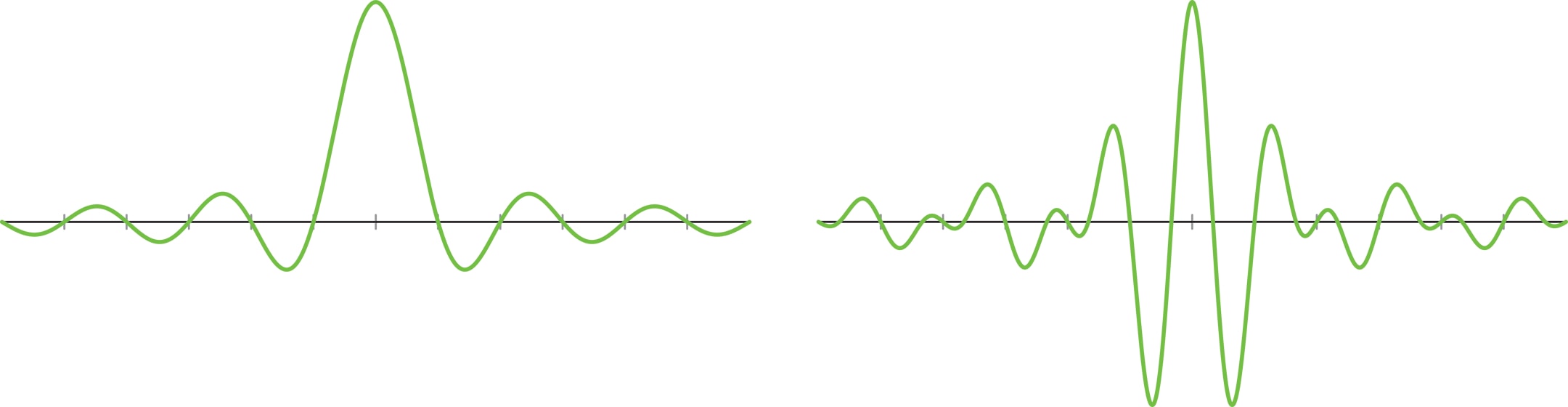
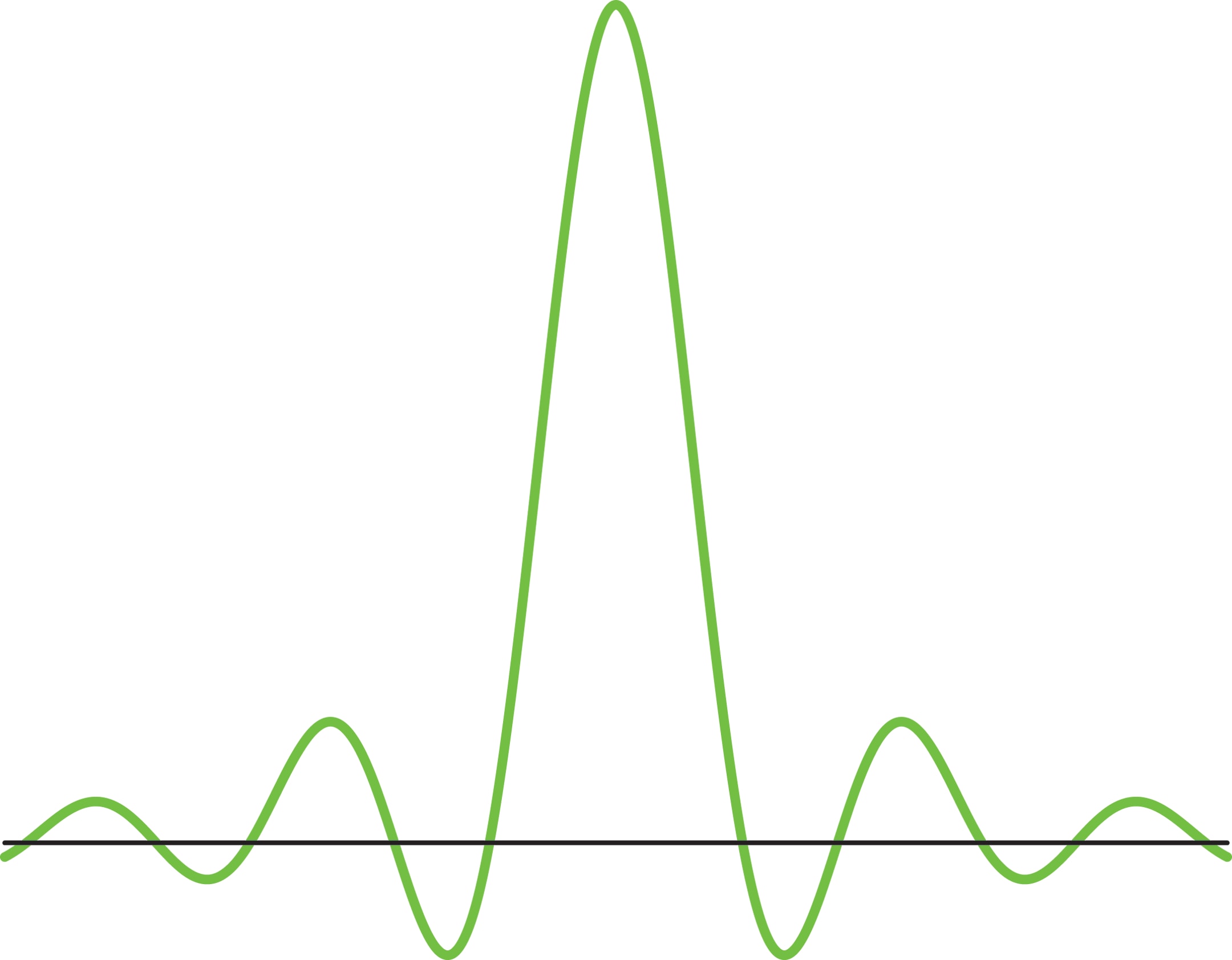
Чтобы избежать эффекта разма­зы­ва­ния шума, надо найти и исполь­зо­вать базис, состо­ящий из лока­ли­зо­ван­ных функций. Так назы­ва­ется функция, у кото­рой все нену­ле­вые зна­че­ния сосре­до­то­чены на небольшом отрезке. Иными сло­вами, нужны не плав­ные волны типа сину­сов и коси­ну­сов, а рез­кие и узкие всплески.

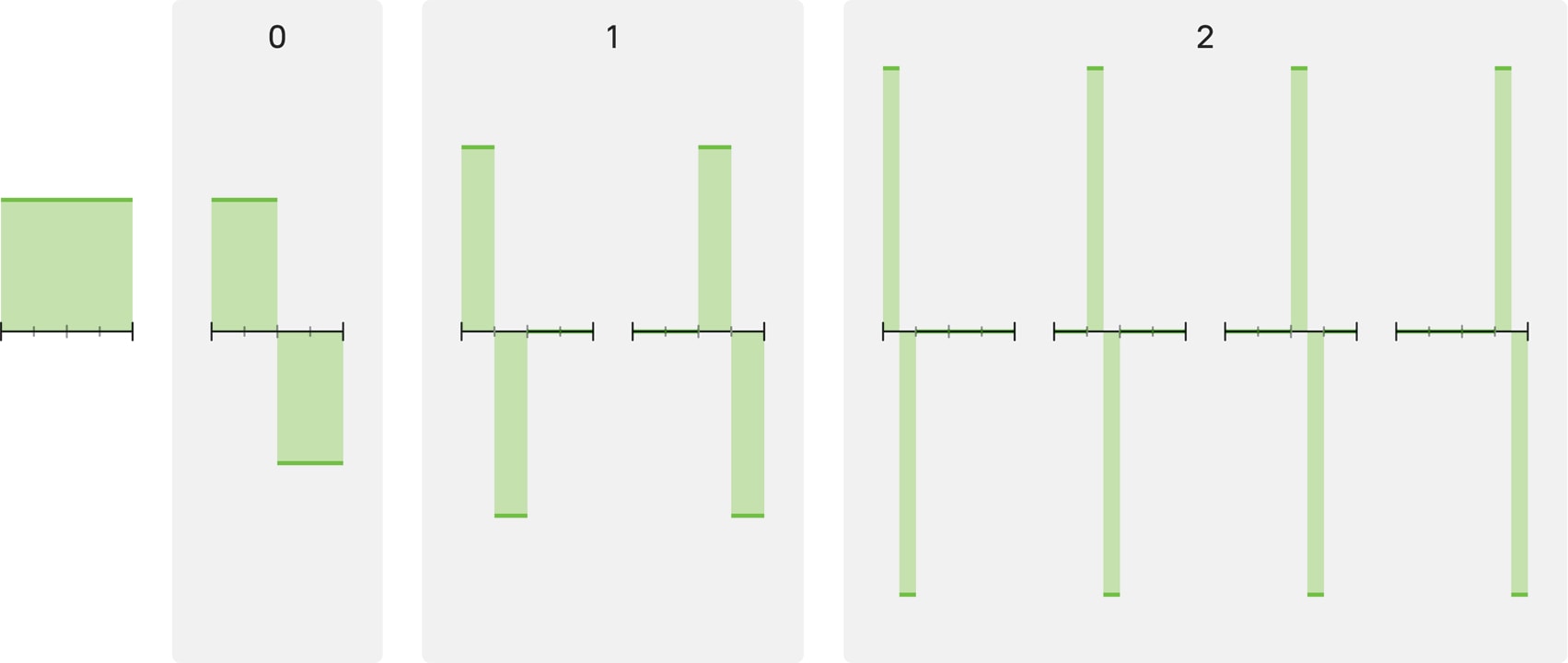
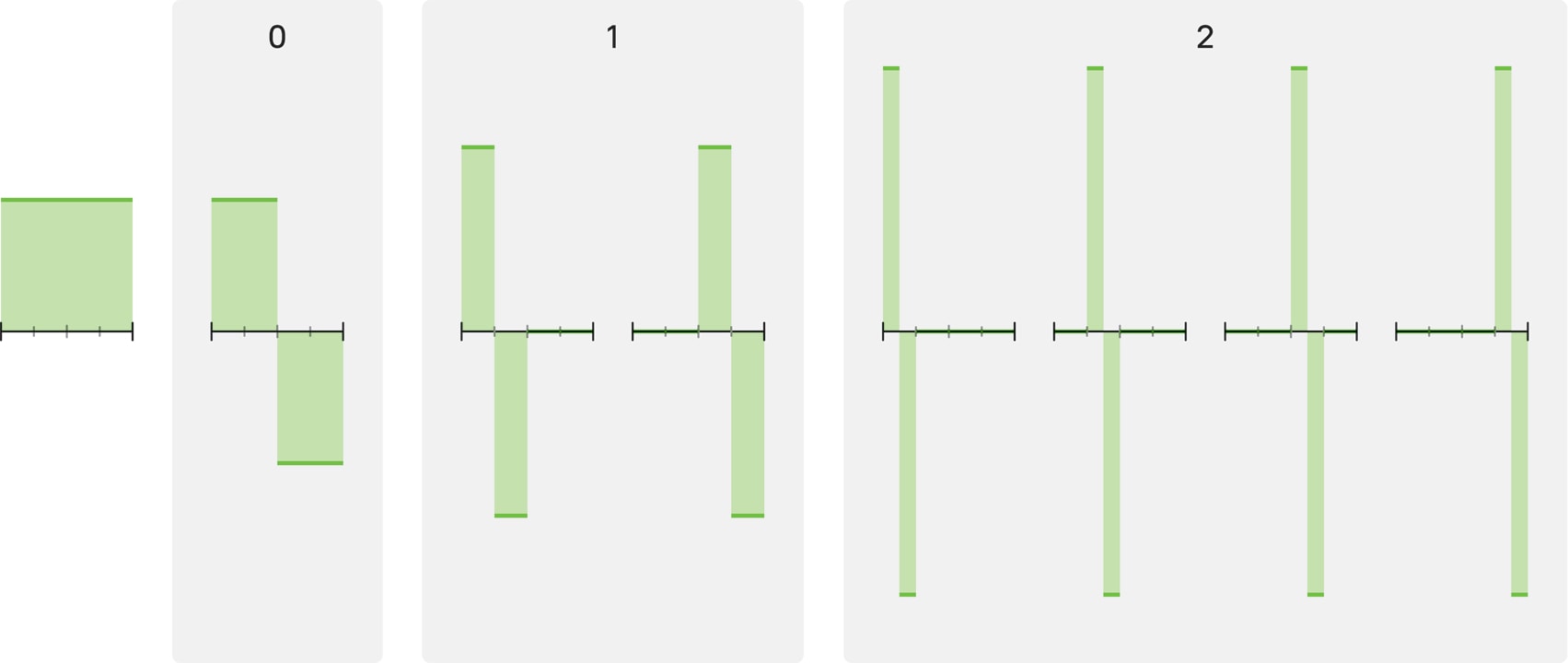
Начало всплес­ков: система Хаара. На пути к базису эффек­тив­ному и состо­ящему из лока­ли­зо­ван­ных функций сде­лаем промежу­точ­ную оста­новку в 1909 году и позна­комимся с бази­сом Хаара. Этот базис удо­бен в исполь­зо­ва­нии, состоит из лока­ли­зо­ван­ных функций, но при этом не очень уда­чен в смысле эффек­тив­но­сти. Базис Хаара на отрезке $[0,1]$ стро­ится после­до­ва­тельно, по уров­ням.

На нуле­вом уровне — всего одна функция $h_1$, «ступенька»: она равна 1 на левой поло­вине отрезка и $(-1)$ — на пра­вой. Из сжа­тий и сдвигов этой функции $h_1$ полу­чаются все после­дующие функции Хаара.

На пер­вом уровне оби­тают две функции, $h_2$ и $h_3$: сжа­тая в два раза ступенька $h_1$ может быть лока­ли­зо­вана и на $[0,1/2)$, и на $[1/2,1)$.

Функции ${h_4,h_5,h_6,h_7}$ вто­рого уровня — это четыре ступеньки, полу­чен­ные сжа­тием $h_1$ в четыре раза и лока­ли­зо­ван­ные на после­до­ва­тель­ных чет­вер­тях отрезка $[0,1]$.

В общем слу­чае уро­вень с номе­ром $n$ состоит из $2^n$ ступе­нек, каж­дая из кото­рых — ступенька $h_1$, сжа­тая в $2^n$ раз.

Функции одного уровня попарно ортого­нальны, так как они рас­по­ложены на непе­ре­се­кающихся отрез­ках. Ортого­наль­ность функций раз­ного уровня дока­зы­ва­ется несложно. Чтобы норма каж­дой функции была равна 1, надо каж­дую ступеньку умножить на коэффици­ент, учи­ты­вающий длину отрезка лока­ли­за­ции.

Если функцию $h_1$, про­должен­ную тож­де­ствен­ным нулём на всю чис­ло­вую прямую, обо­зна­чить через $\psi$, то все функции Хаара $\{h_k\}$ можно опи­сать одной форму­лой: $2^{n/2}\>\psi(2^n t - k)$, где $n\ge 0$, а при фик­си­ро­ван­ном $n$ параметр $k$ меня­ется от 0 до $2^n-1$. Чтобы система стала орто­норми­ро­ван­ным бази­сом, надо доба­вить к ней ещё одну функцию $h_0= 1$.

В про­стран­стве всех функций функции Хаара $\{h_k\}_{k=0}^{2^n-1}$ задают плос­кость $V_n$ размер­но­сти $2^n$. Базис про­стран­ства $V_n$ — объеди­не­ние функций всех уров­ней от 0 до $n-1$. Ана­логично системе Фурье, наи­лучший элемент при­ближе­ния функции $f$ в подпро­стран­стве $V_n$ — про­екция $$\textstyle S_nf=\sum\limits_{k=0}^{2^n-1} (f, h_k) h_k.$$ При про­еци­ро­ва­нии на $V_n$ любая функция $f$ пре­враща­ется в «лесенку» из $2^n$ ступе­нек. Высота каж­дой ступеньки есть сред­нее зна­че­ние функции на соот­вет­ствующем интер­вале.

Дис­крет­ный вари­ант базиса Хаара $\{H_k\}$ — про­норми­ро­ван­ные зна­че­ния функций $\{h_k\}$ на сетке с шагом $1/2^n$. Система $\{H_k\}_{k=0}^{2^n-1}$ — орто­норми­ро­ван­ный базис в $\mathbb R^N$, $N=2^n$.

Даже прямое вычис­ле­ние всех коэффици­ен­тов в базисе $\{H_k\}$ имеет слож­ность вдвое меньшую, чем для быст­рого пре­об­ра­зо­ва­ния Фурье. Это след­ствие дво­ич­ной струк­туры базиса Хаара. Но и эту низ­кую слож­ность можно уменьшить! В так назы­ва­емом кас­кад­ном алго­ритме исполь­зу­ется фак­ти­че­ская повто­ря­емость действий в дис­крет­ном пре­об­ра­зо­ва­нии Хаара, обу­слов­лен­ная дво­ич­но­стью и «пра­виль­ным» чере­до­ва­нием зна­ков функций $\{H_k\}$. В итоге достига­ется слож­ность $4(N-1)$ — по порядку неулучша­емый результат, в сред­нем менее четырёх опе­раций на каж­дый коэффици­ент!

В дис­крет­ном пре­об­ра­зо­ва­нии Хаара, в отли­чие от пре­об­ра­зо­ва­ния Фурье, шум, появившийся в одной коор­ди­нате век­тора $x$, меняет не все коэффици­енты в раз­ложе­нии $x$ по базису $\{H_k\}_{k=0}^{2^n-1}$, а только $n+1$, по одной коор­ди­нате на каж­дом уровне. Число $n+1$ мало по срав­не­нию с $N=2^n$, т. е. пре­об­ра­зо­ва­ние Хаара сохра­няет лока­ли­зо­ван­ность помех.

Каза­лось бы, иде­аль­ная система, но… У базиса Хаара тоже есть недо­статки. Глав­ный из них — ско­рость при­ближе­ния функции пере­стаёт расти с воз­рас­та­нием глад­ко­сти. Напри­мер, функции класса $C^3$ при­ближаются не лучше, чем функции из класса $C^1$. Это ведёт к мед­лен­ной схо­димо­сти раз­ложе­ний Хаара и, как след­ствие, к необ­хо­димо­сти хра­нить большое число коэффици­ен­тов.

Дру­гой недо­ста­ток функций Хаара — они раз­рыв­ные. А это сужает тех­ни­че­ские возмож­но­сти. Во многих при­ложе­ниях при­ближе­ние функции (сиг­нала) при­хо­дится диффе­ренци­ро­вать, иногда даже несколько раз (скажем, при чис­лен­ном реше­нии диффе­ренци­аль­ных урав­не­ний). С функци­ями Хаара этого делать нельзя, они не только не диффе­ренци­ру­емы, но и не непре­рывны.

Зна­чит, в иде­але, для при­ближе­ний нужен «глад­кий Хаар»!

Всплески: общая кон­струкция. Мы двига­лись в изложе­нии «парал­лельно» раз­ви­тию тео­рии при­ближе­ний функций, про­пу­стив ряд важ­ных оста­но­вок — много­чис­лен­ные достиже­ния на этом пути. Накоп­лены идеи, благо­даря кото­рым в 1980-х годах про­изошла кри­стал­ли­за­ция понима­ния того, как должны выгля­деть всплески — «пра­виль­ный» базис в про­стран­стве функций со ска­ляр­ным про­из­ве­де­нием на чис­ло­вой прямой $\mathbb R$.

Общее пред­став­ле­ние базиса всплес­ков даётся на языке линей­ных про­странств, плос­ко­стей, кото­рые порож­даются конеч­ными набо­рами элемен­тов базиса. Терми­но­логи­че­ски такое пред­став­ле­ние назы­ва­ется крат­но­масштаб­ным ана­ли­зом: это система замкну­тых подпро­странств $\{V_n\}_{n \in \mathbb Z}$ в про­стран­стве функций, обла­дающая сле­дующими свойствами.

1. Про­стран­ства $V_n$ расши­ряются: $V_n\subset V_{n+1}$, $V_n\ne V_{n+1}$.

2. Про­стран­ства $V_n$ «исчерпы­вают» всё про­стран­ство функций при $n\to \infty$: любую функцию можно при­бли­зить сколь угодно точно функци­ями из неко­то­рого про­стран­ства $V_n$.

3. Пере­се­че­ние всех про­странств $V_n$ содержит только нуле­вую функцию (тож­де­ствен­ный нуль).

4. Расши­ре­ние в системе $\{V_n\}$ носит дво­ич­ный харак­тер: для любой функции $f(t)\in V_n$ имеем  $f(2t)\in V_{n+1}$.

5. Про­стран­ство $V_0$ порож­дено ортого­наль­ными друг другу целыми сдвигами неко­то­рой функции $\varphi$.

С помощью функции $\varphi$ можно постро­ить всплеск-функцию $\psi$, сдвиги и сжа­тия кото­рой обра­зуют систему всплес­ков, являющуюся орто­норми­ро­ван­ным бази­сом в про­стран­стве функций: $$\psi_{n , k} (t) = 2^{n/2}\> \psi(2^n t - k),\qquad n{,} k \in \mathbb Z.$$ Каж­дый крат­но­масштаб­ный ана­лиз порож­дает систему всплес­ков, и любая система всплес­ков порож­да­ется неко­то­рым крат­но­масштаб­ным ана­ли­зом. Поэтому постро­е­ние системы всплес­ков сво­дится к постро­е­нию функции $\varphi$.

Базисы, порож­да­емые системами крат­но­масштаб­ного ана­лиза, в силу своей дво­ич­ной при­роды обла­дают рядом пре­имуществ. Во‐пер­вых, коэффици­енты раз­ложе­ния быстро вычис­ляются с исполь­зо­ва­нием кас­кад­ного алго­ритма. Во‐в­то­рых, и это глав­ное, пере­ход от плос­ко­сти $V_n$ к $V_{n+1}$ озна­чает, что в задаче о при­ближе­нии число исполь­зу­емых базис­ных функций уве­ли­чи­ва­ется вдвое, что явля­ется оптималь­ным спо­со­бом достиже­ния задан­ной точ­но­сти.

Отме­тим, что усло­вия на про­стран­ства $V_n$ в опре­де­ле­нии крат­но­масштаб­ного ана­лиза обес­пе­чи­вают то, что система $\{\psi_{n, k} (t)\}$ будет бази­сом в про­стран­стве функций на прямой.

Всплески: при­меры. Постро­ен­ный базис Хаара на отрезке $[0,1]$ — всё ещё не система всплес­ков. Он пре­враща­ется в тако­вую с помощью рас­про­стра­не­ния на всю прямую $\mathbb R$. Всплески Хаара порож­даются функцией $\varphi$ — харак­те­ри­сти­че­ской функцией промежутка $[0,1)$, кото­рая равна 1 на нём и 0 вне него, а также функцией $\psi$, полу­чен­ной про­долже­нием нулём на $\mathbb R$ функции Хаара $h_1$. Всплески Хаара обла­дают пре­крас­ной лока­ли­за­цией, но насле­дуют и недо­статки системы Хаара (огра­ни­чен­ность ско­ро­сти при­ближе­ния при росте глад­ко­сти, раз­рыв­ность функций системы).

Всплески Шен­нона—Котель­ни­кова доста­точно есте­ствен­ным обра­зом воз­ни­кают в элек­тро­нике, поэтому инже­неры при­думали эту систему раньше матема­ти­ков (в пер­вой поло­вине XX века). Крат­но­масштаб­ный ана­лиз про­странств функций порож­дён функцией $\varphi$ и соот­вет­ствует системе всплес­ков с функцией $\psi$, где $$ \varphi (t)= \frac{\sin π t}{π t},\qquad \psi (t)= \frac{\sin 2π t - \sin π t}{π t}. $$

(Тех­ни­че­ское пояс­не­ние для ана­ли­ти­ков: функция $\varphi$ — пре­об­ра­зо­ва­ние Фурье харак­те­ри­сти­че­ской функции отрезка. Так что воз­ни­кающая система всплес­ков в каком‐то смысле двойственна системе Хаара.)

Полу­чающи­еся всплески Шен­нона—Котель­ни­кова очень глад­кие, но при этом далеки от лока­ли­зо­ван­ных: мед­ленно убы­вают при $t \to \infty$. Пло­хая лока­ли­за­ция затруд­няет избав­ле­ние сиг­нала от шума и замед­ляет работу кас­кад­ного алго­ритма. Это глав­ный недо­ста­ток дан­ной системы.

Всплески Мейера. В 1986 году Ив Мейер немного «подпра­вил» систему Шен­нона—Котель­ни­кова, полу­чив глад­кую и быстро убы­вающую систему всплес­ков. Эта малая поправка, однако, далась большими уси­ли­ями, ведь новая система должна была сохра­нить все свойства всплес­ков Шен­нона—Котель­ни­кова. (Изме­не­ние можно пояс­нить так: в отли­чие от системы Шен­нона—Котель­ни­кова, теперь функция $\varphi(t)$ явля­ется пре­об­ра­зо­ва­нием Фурье сглажен­ной харак­те­ри­сти­че­ской функции отрезка, а такая функция $\varphi(t)$ быстро убы­вает при $t \to \infty$.) Полу­чи­лась заме­ча­тель­ная система функций, кото­рая до сих пор широко исполь­зу­ется. В отли­чие от ранее извест­ных систем, всплески Мейера не были взяты «из жизни», а пол­но­стью, от начала до конца, при­думаны. Это — чисто матема­ти­че­ская кон­струкция, при­чём очень хит­рая и тон­кая. За её изоб­ре­те­ние Мейер полу­чил множе­ство науч­ных наград, вклю­чая пре­стиж­нейшую премию Абеля в 2017 году.

При всех своих досто­ин­ствах, всплески Мейера — это ещё не «глад­кий Хаар», поскольку всплеск-функция не обраща­ется в нуль вне неко­то­рого отрезка (хотя и быстро стремится к нулю).

Всплески Добеши были изоб­ре­тены в 1988 году и про­из­вели сен­сацию в науч­ном сообще­стве. На Меж­ду­на­род­ном конгрессе матема­ти­ков в Цюрихе в 1994 году Ингрид Добеши, вопреки обык­но­ве­нию, было дано два часа для пле­нар­ного доклада, вме­сто при­ня­того одного часа. Новые базисы уже не задаются явными форму­лами, а стро­ятся как реше­ния спе­ци­аль­ных урав­не­ний. Вычис­ляются они при­ближённо с неко­то­рой точ­но­стью. Базис ные функции имеют конеч­ную глад­кость, в отли­чие от систем Шен­нона—Котель­ни­кова и Мейера. Более того, они имеют много общего с фрак­та­лами. Тем не менее они обла­дают всеми необ­хо­димыми свойствами: хорошо при­ближают сиг­налы и поз­во­ляют уда­лять шумы. А самое глав­ное, как и для системы Хаара, функции системы Добеши сосре­до­то­чены на конеч­ных отрез­ках. Сей­час они исполь­зуются повсе­местно при работе с фото- и видео­изоб­раже­ни­ями, в компью­тер­ной томографии, при рас­по­зна­ва­нии обра­зов и т. д. Напри­мер, стан­дарт JPEG2000 осно­ван на всплес­ках Добеши.

Заклю­че­ние. Под­ве­дём итоги рас­сказа о зада­чах эко­ном­ного пред­став­ле­ния сиг­на­лов. Два века назад появи­лась тео­рия рядов Фурье. Сто­ле­тием позже появи­лись пер­вые всплески (функции Хаара), ещё через 80 лет воз­никли всплески Добеши. Именно столько времени пона­до­би­лось учё­ным для созда­ния тео­рии всплес­ков, нашед­шей пло­до­твор­ные при­ложе­ния. Тео­рия про­должает интен­сивно раз­ви­ваться, в ней оста­ётся много нерешён­ных инте­рес­ных задач.