Знание элементарных свойств чисел и умение безошибочно выполнять простейшие арифметические действия позволят вам удивить друга, представ перед ним в роли математического мага.
Например, попросите друга проделать следующие действия: загадать натуральное число; прибавить к нему 5; умножить результат на 2; вычесть из полученного загаданное число; проделать последнюю операцию ещё раз. После выполнения всех операций вы можете поразить друга, сказав, что знаете полученное число — 10.
Прозрачность фокуса становится очевидной, если словесную инструкцию операций с задуманным числом $x$ представить как последовательность арифметических действий: $(x+5)\cdot 2 -x -x=10$.
«Дар предвидения» можно проявить и в случае, если итоговый результат оказывается задуманным числом (независимо от его значения). Попросите друга задумать трёхзначное число и записать его подряд дважды. Полученное шестизначное число предложите разделить на 7, полученное — на 11, и ещё раз — на 13. Во‐первых, шестизначное число разделится нацело, во‐вторых, результатом окажется задуманное число.
Секрет фокуса раскрывают два факта: результат умножения трёхзначного числа на 1001 совпадает с тем, что получается, если это число выписать дважды подряд (шесть цифр); а разложение на множители числа 1001 имеет вид $1001=7\cdot 11\cdot 13$.
Делимость чисел (включая деление с остатком) — важный источник, механизм арифметических фокусов. Попросите друга загадать двузначное число (не меньше дюжины); умножить это число на 9; назвать любые две цифры получившегося трёхзначного числа. После этого вы сразу называете третью цифру.
Признак делимости на 9, основа фокуса, выводится из представления трёхзначного числа по сотням, десятками и единицам: $100a+10b+c=(99a+9b)+(a+b+c)$. В этом разбиении первая скобка делится на 9, поэтому делимость числа на 9 равносильна делимости на 9 суммы его цифр $(a+b+c)$.
В фокусе трёхзначное число — результат умножения задуманного числа на 9, поэтому надо подобрать третью цифру так, чтобы сумма всех цифр делилась на 9. Если сумма названных другом двух цифр не равна 9, то это делается однозначно, а вот если она равна 9, то придётся предложить два варианта: третьей цифрой может быть и 0, и 9.
Другой тип фокусов — угадывание задуманного числа. В качестве примера научимся «определять» день рождения незнакомого человека: день $x$ и месяц $y$. Попросите незнакомца умножить $x$ (день рождения) на 2; прибавить 5; умножить полученную сумму на 50; прибавить $y$ (месяц рождения) и вслух назвать полученное число. После этого вы сможете назвать дату рождения: день и месяц.
Объяснение фокуса опять дают формулы, в которых записаны действия: $(x\cdot 2+5)\cdot 50 +y=100x+y+250$. Здесь $y$ — однозначное или двузначное число, от 1 до 12, поэтому его добавление к $100x$ не «портит» цифровую запись $x$. Например, 29 марта в виде $100x+y$ предстанет как 2903, а 22 декабря — как 2212.
Теперь можно сформулировать правило для фокусника: из числа, названного незнакомцем, надо мысленно вычесть 250, в полученном числе последние две цифры представляют $y$, а остальные — $x$.
Понятно, что можно придумать множество подобных «волшебных» инструкций. Но иногда простые с виду инструкции отправляют начальное число в путешествие, длительность и результат которого невозможно даже оценить. Вот одна из нерешённых математических проблем, сформулированная в далёком 1937 году.
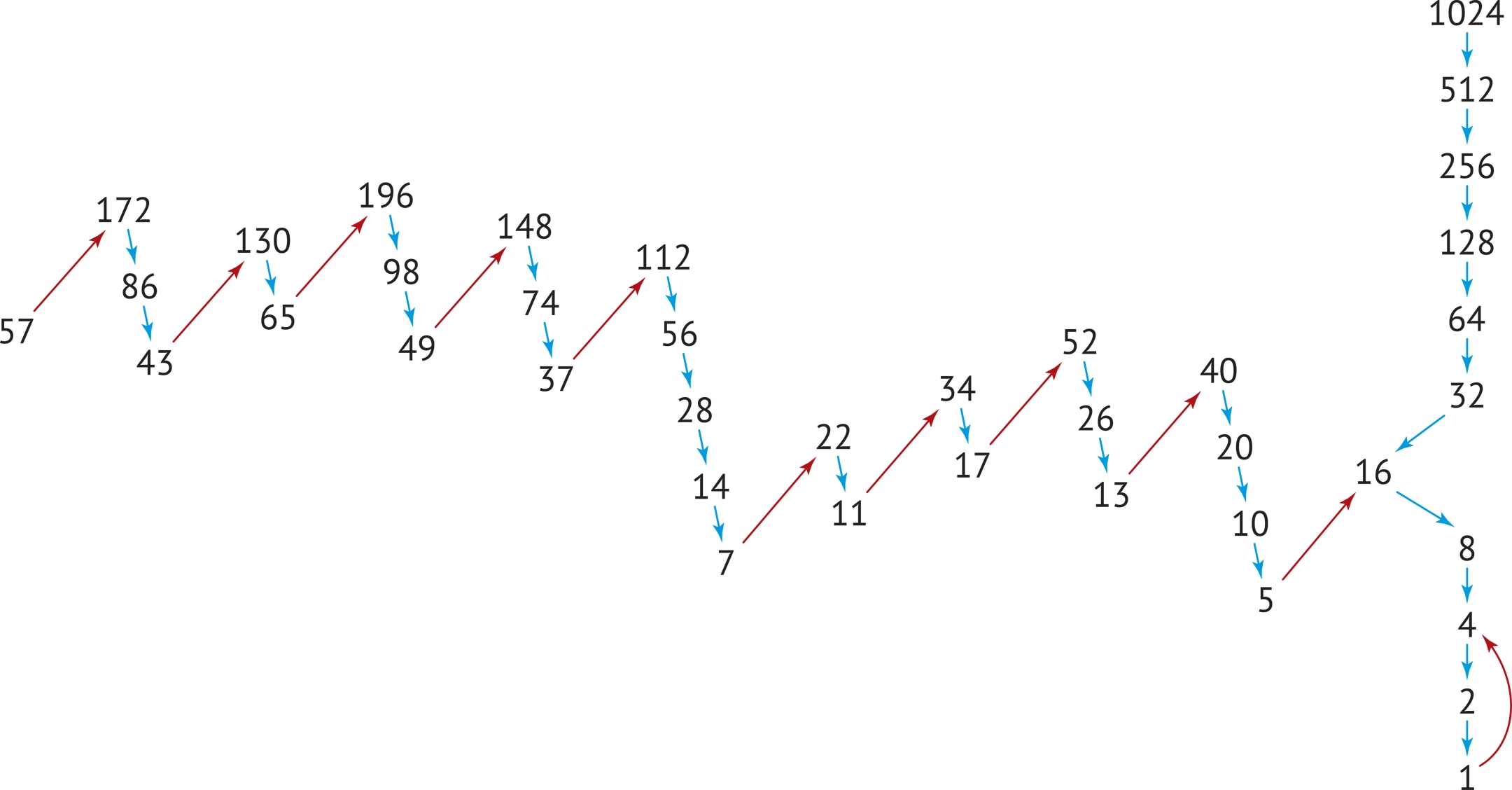
Пусть $n$ — натуральное число. Если число нечётное, то оно увеличивается, превращаясь в $3n+1$; а если чётное — то уменьшается, переходит в $n/2$. С новым значением проводят те же операции.
Что победит — рост «$3n+1$» или падение «$n/2$»? Гипотеза, названная именем немецкого математика Л. Коллатца, утверждает, что рано или поздно процесс приведёт в 1 (и далее $1\to 4\to 2\to 1$).
Например, очевидно, что гипотеза верна для начальных чисел вида $2^k$. Предположим, удалось проверить, что для чисел из какого‐то множества гипотеза верна. Тогда рассмотрение траектории выбранного начального числа достаточно проводить до попадания в «проверенную область»: дальнейший результат предрешён.
Строгого доказательства гипотезы Коллатца до сих пор нет, хотя с помощью компьютера она проверена для всех чисел до $10^{18}$.
Кордемский Б. А. Математическая смекалка. — М.: ГИТТЛ, 1954. — [Глава 10 «Математические игры и фокусы»].
Гарднер М. Математические чудеса и тайны. Математические фокусы и головоломки. — 3‐е изд. — М.: Наука, 1978.
Перельман Я. И. Ящик загадок и фокусов. — М.—Л.: ГПЗ, 1929. — [Переиздание: М.: ИД Мещерякова, 2008].
Перельман Я. И. Занимательные задачи и опыты. — М.: Детгиз, 1959.
Гарднер М. Крестики‐нолики. — М.: Мир, 1988. — [Глава 18 «Ползунок, $3x+1$ и другие любопытные вопросы»].
Хэйес Б. Взлёты и падения чисел-градин