Слово «логарифм» читателю знакомо, известны ему также логарифмическая функция и логарифмическая линейка. Зато может удивить то, что человек, оценивая параметры внешних раздражителей, зачастую подсознательно их логарифмирует. Например, так происходит с громкостью звука и яркостью света.
В XIX веке на основе многочисленных опытов был сформулирован закон Вебера—Фехнера. В нём изменения ощущений человека количественно связаны с изменением внешних раздражителей. В частности, было установлено, что человек оценивает изменение громкости звукового воздействия в относительной шкале: важно не абсолютное значение «новой громкости», а его отношение к значению «начальной громкости». Получается, что организм человека настроен природой на восприятие изменений «в разы» (скажем, он чувствует рост в $1,2$ раза), а не «на сколько-то».
Например, в экспериментах Вебера было обнаружено, что если добавить к 60 горящим свечам ещё одну, то наблюдатель заметит изменение яркости. А при 120 горящих свечах изменение яркости будет замечено только при добавлении двух свечей.
Обычно создание шкалы величин основывается на «аддитивном» принципе: сколько шагов длины $a$ надо сделать, чтобы пройти расстояние $b$? Иначе говоря, сколько раз надо сложить c собой $a$, чтобы получить $b$? А можно использовать «мультипликативный» принцип: сколько раз надо умножить на себя величину $a$ (в какую степень надо возвести $a$), чтобы получить $b$?
Второй подход приводит к понятию логарифма: по определению $\log_a b=m$, если $a^m=b$. В термине «логарифм» один из создателей логарифмов Джон Непер, математик и астроном, соединил два слова из древнегреческого: $\lambda\acuteογο\varsigma$ — отношение (в нашем, «мультипликативном» смысле) и $α \rho \iota\mkern1mu \theta μ \acute ο \varsigma$ — число.
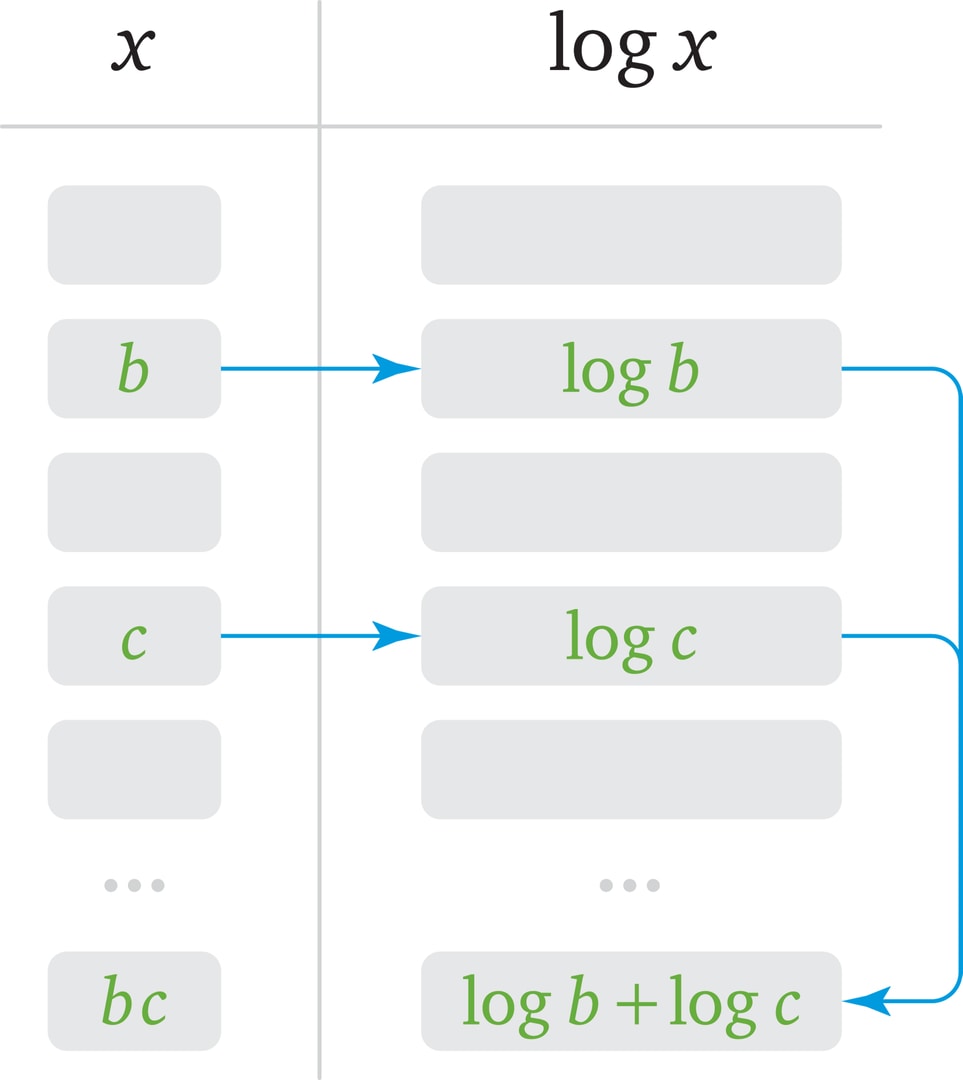
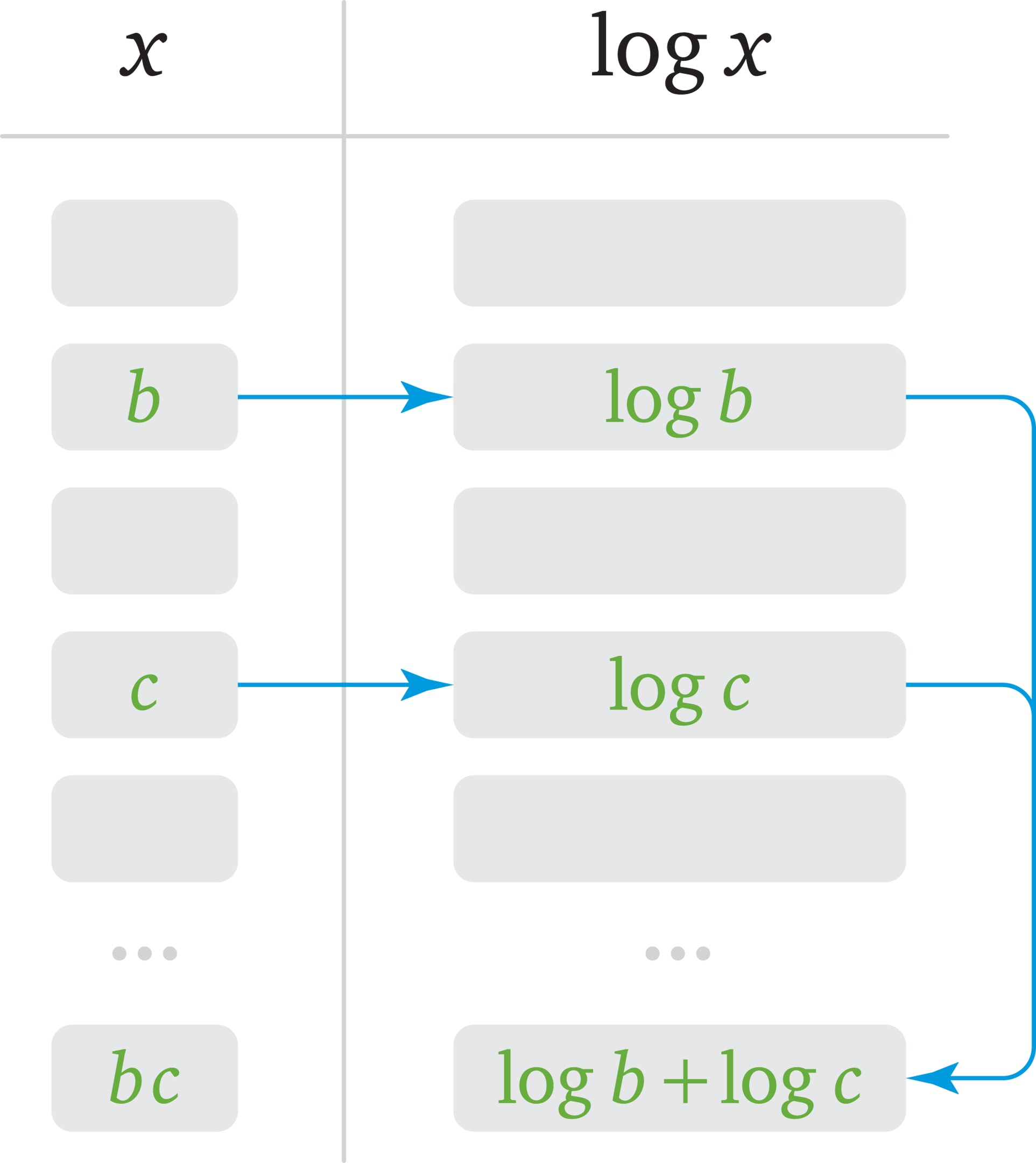
Одним из основных свойств логарифмов является следующее: $$ \log_a (bc)=\log_a b+\log_a c. $$
Это соотношение устанавливает связь между операциями сложения и умножения — логарифм произведения равен сумме логарифмов. Сложение — более простая, более «быстрая» операция, чем умножение, а приведённое свойство позволяет свести вычисление произведения чисел к сложению их логарифмов.
Исторически первая вычислительная роль логарифмов была связана с этим свойством. Если у вычислителя есть таблица, в которой «подробно», с малым шагом, представлены числа и их логарифмы (по фиксированному основанию, например, при $a=10$), то вычисление произведения $bc$ распадается на последовательность несложных шагов. В таблице находим числа $b$ и $c$ (или близкие к ним), определяем по таблице их логарифмы, складываем эти логарифмы и по таблице подбираем число, логарифм которого близок к найденному значению. Появление такого способа приближённого умножения было особо оценено астрономами, работавшими с «астрономически» большими числами.
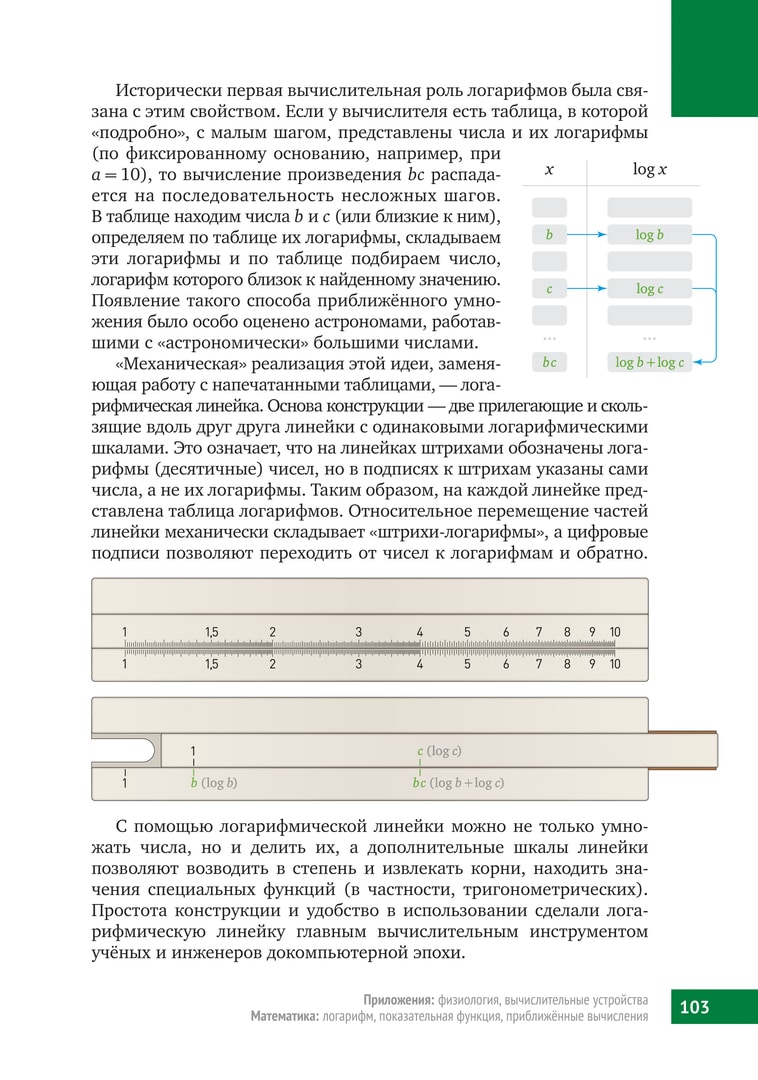
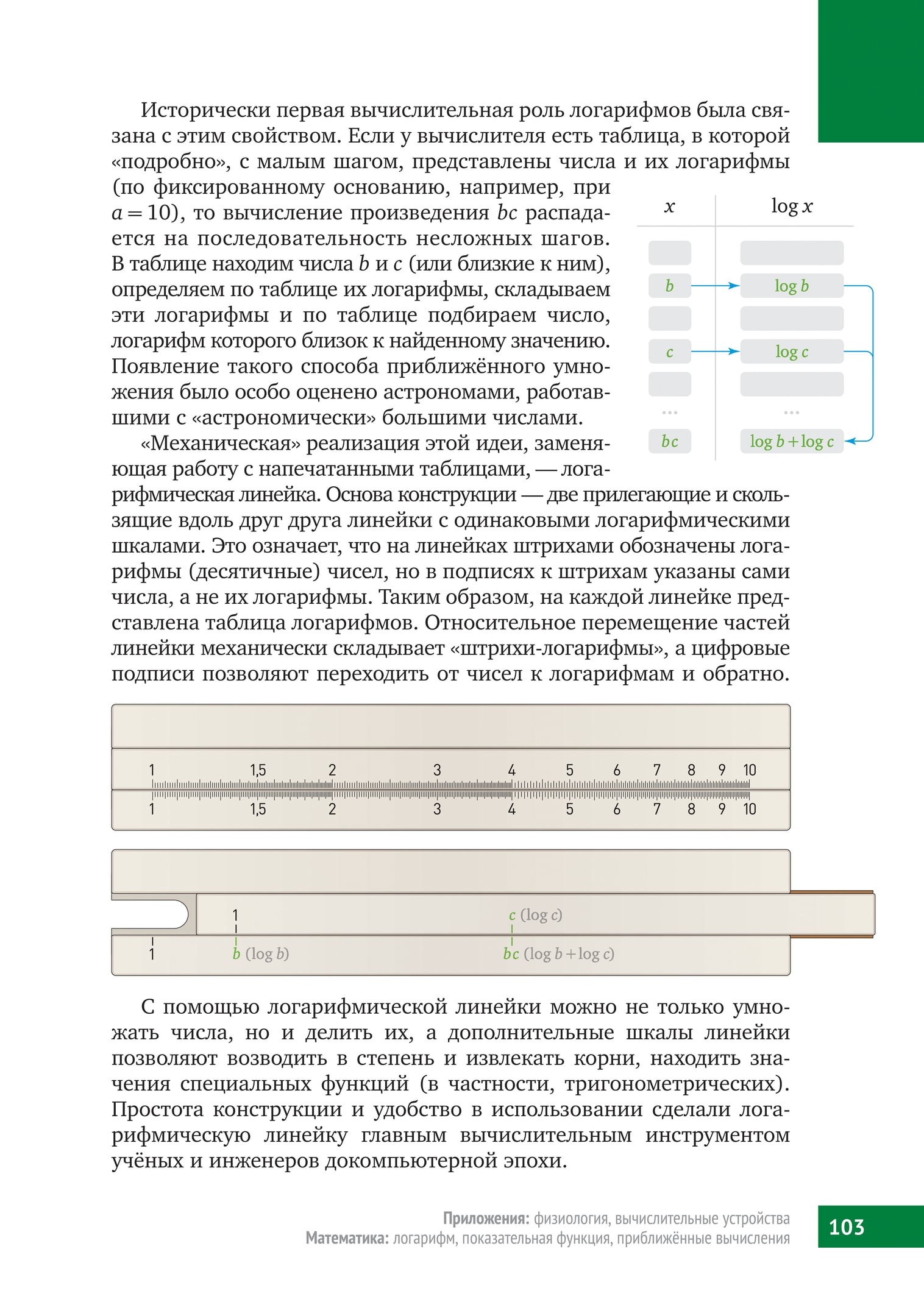
«Механическая» реализация этой идеи, заменяющая работу с напечатанными таблицами, — логарифмическая линейка. Основа конструкции — две прилегающие и скользящие вдоль друг друга линейки с одинаковыми логарифмическими шкалами. Это означает, что на линейках штрихами обозначены логарифмы (десятичные) чисел, но в подписях к штрихам указаны сами числа, а не их логарифмы. Таким образом, на каждой линейке представлена таблица логарифмов. Относительное перемещение частей линейки механически складывает «штрихи-логарифмы», а цифровые подписи позволяют переходить от чисел к логарифмам и обратно.
С помощью логарифмической линейки можно не только умножать числа, но и делить их, а дополнительные шкалы линейки позволяют возводить в степень и извлекать корни, находить значения специальных функций (в частности, тригонометрических). Простота конструкции и удобство в использовании сделали логарифмическую линейку главным вычислительным инструментом учёных и инженеров докомпьютерной эпохи.
Ещё одно важное свойство логарифмов, объясняющее их особую роль в вычислениях и аналитических исследованиях: логарифм большого числа намного меньше самого числа. Например, число атомов в наблюдаемой части Вселенной оценивается как $10^{80}$ — огромное число. А десятичный логарифм этого числа вполне «осязаем»: 80.
У быстро растущих функций, таких как $y=10^{kx}$, есть несколько неприятных особенностей. Во‐первых, при больших значениях $x$ график функции так быстро убегает вверх, что и на книжной странице, и на экране монитора от него останется лишь небольшой, узкий кусочек, а остальная часть окажется вне страницы или экрана. Во‐вторых, в повседневной жизни человек редко сталкивается с большими изменениями чего-либо за небольшое время, исторически к этому не подготовлен (катастрофы типа извержений вулканов или землетрясений — редкие исключения). Неудивительно, что при встрече с резкими перепадами значений показательной функции ($y=a^x$) возникает желание сгладить эти перепады, заменить функцию более «спокойной», пологой. По обеим приведённым причинам удобно от функции $y=10^{kx}$ перейти к функции $z=\lg y = kx$.
В естествознании многие законы записываются с использованием показательных функций. Подобные формулы возникают, если закон относится к процессу, в математическом описании которого основную роль играют линейные дифференциальные уравнения первого порядка. Переход к логарифмам делает запись таких законов более «дружелюбной», график линейной функции $z=kx$ (прямая) не просто проще графика показательной функции $y=10^{kx}$, его простота становится действенным инструментом исследования.
Рассмотренное понятие логарифма позволяет привести аналитическую формулировку закона Вебера—Фехнера: $S=k\lg \frac{P}{P_0}$. В этой формуле $S$ — интенсивность ощущения человека, $P$ — сила внешнего раздражителя, $P_0$ — нижнее пороговое значение силы раздражителя (т. е. при $P<P_0$ раздражитель не воспринимается, ощущений нет), $k$ — константа.
Получается, и мы об этом уже говорили, что человек воспринимает изменение силы внешнего воздействия в разы (для логарифмов этих величин — «на сколько-то»). Универсальность закона Вебера—Фехнера приводит к необходимости использования шкалы, в которой главная характеристика — не абсолютные значения величин, а их отношение.
В частности, этим законом описывается и то, как человек воспринимает звуковое воздействие. Поэтому логарифмическая шкала становится естественной. Другой довод в пользу этой шкалы — широкий диапазон значений воспринимаемых человеческим ухом громкостей: отношение громкостей максимального «безопасного» для человека звука и минимального из воспринимаемых равно $10^{15}$. Сравнивать абсолютные значения при столь гигантском разбросе неудобно, в отличие от сравнения в логарифмической шкале, устроенной по мультипликативному принципу. Говорят, что две громкости отличаются на 1 бел, если отношение громкостей равно 10, т. е. $\frac{P_2}{P_1}=10$, $\lg \frac{P_2}{P_1}=1$ (бел). На практике чаще используется более мелкая единица — децибел, равная $0,1$ бел.
В физике и технике идея подобного «сравнительного» измерения одноимённых величин широко применяется (громкость, яркость, мощность, энергия и др.). Для создания шкалы в таких измерениях удобно выделить базовый, опорный уровень. Например, при измерении звука опорный уровень $P_0$ — это минимальная для слуха пороговая величина.
Перевод кратного изменения громкости в аддитивную шкалу в децибелах (логарифмирование) позволяет создать на звуковоспроизводящем устройстве удобную регулировку: изменение громкости в определённое число раз независимо от исходной громкости реализуется поворотом ручки на постоянный угол или передвижением ползунка на постоянное расстояние.
Яркость световых раздражителей человек также воспринимает «логарифмически». Поэтому регулировку настроек фотоаппарата тоже можно сделать на основе равномерной шкалы. Каждая ступень экспозиции фотоаппарата меняет количество излучения, которое попадает на светочувствительный элемент (матрицу или фотоэмульсию) в два раза. Ступень выдержки меняет в два раза время экспозиции, а ступень диафрагмы — площадь отверстия, через которое свет попадает на матрицу. Т. е. обе шкалы устроены «мультипликативно», их значения образуют геометрическую прогрессию. Логарифмы этих величин образуют уже арифметическую прогрессию, что позволяет расположить засечки шкалы диафрагмы равномерно. Если бы шкала не была равномерной, то пользоваться кольцом диафрагмы было бы неудобно — переходы от ступени к ступени отличались бы углами поворота кольца.
Итак, с помощью логарифмов можно не только описать нашу способность «логарифмировать» ощущения, но и проектировать удобные и полезные устройства.
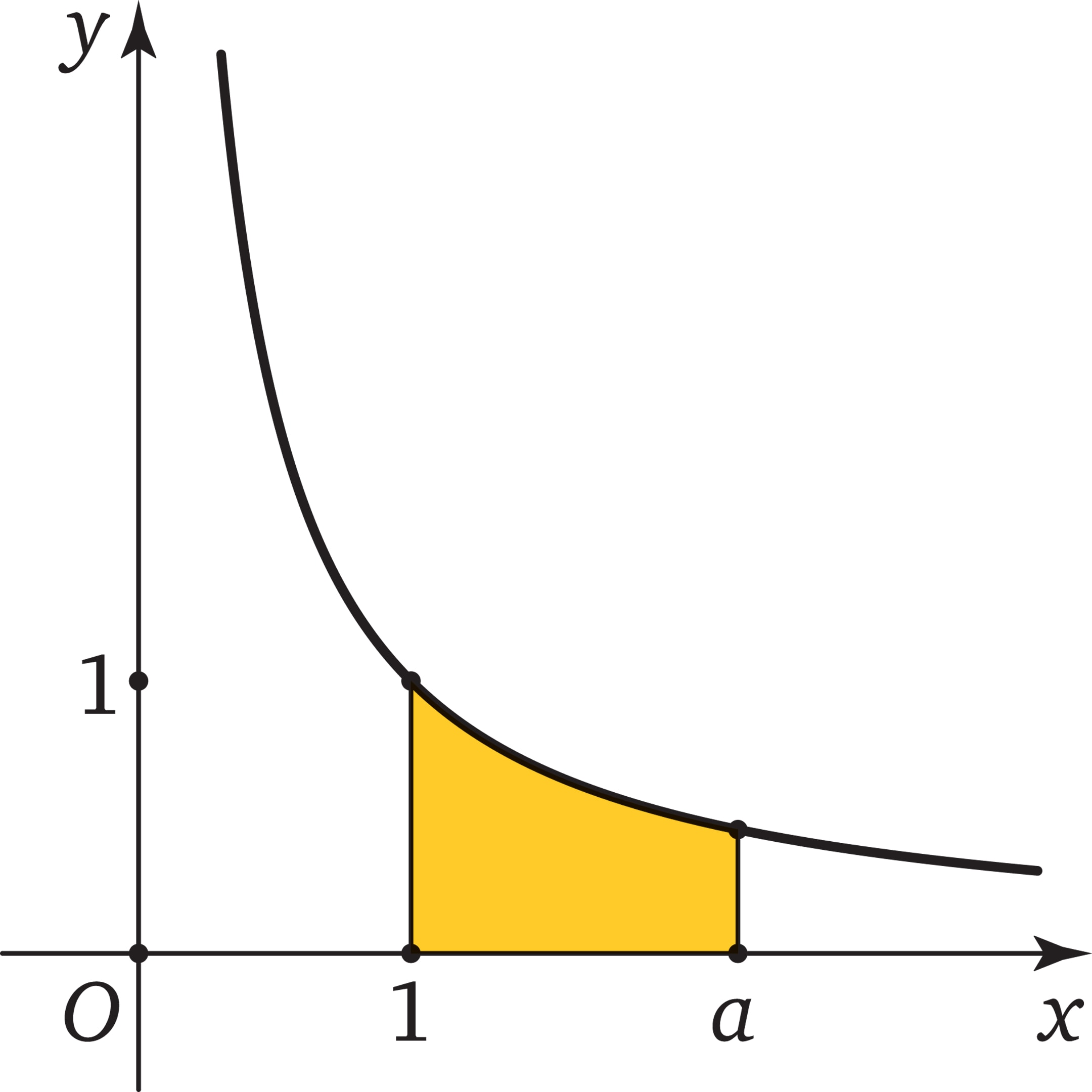
Термины (об этимологии слова «термин» см. «Полярный день») «гипербола» и «логарифм», разрозненно встречающиеся и в школьном курсе математики, и в этой книге, оказываются тесно связанными, причём наглядногеометрически. Площадь криволинейной трапеции под гиперболой $у=\frac{1}{x}$ на участке от $x=1$ до $x=a$ равна $\ln a$ (обозначение натурального логарифма, основание которого — число $e$).
Дело в том, что эта площадь равна определённому интегралу $\int\limits_1^a \frac{dx}{x}$, а поскольку $\frac{1}{x}$ — производная функции $y=\ln x$ (при $x>0$), то $$ \int\limits_1^a \frac{dx}{x}= \ln a - \ln 1= \ln a. $$
Представление о логарифмах как о площадях можно найти в книге А. И. Маркушевича «Площади и логарифмы» (Серия «Популярные лекции по математике»; Вып. 9).
Абельсон И. Б. Рождение логарифмов. — М.—Л.: ОГИЗ, ГИТТЛ, 1948.
Панов Д. Ю. Счётная линейка. — 25‐е изд. — М.: Наука, 1982.
Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — Т. 2: Пространство, время, движение. — М.: Мир, 1965. — [§ 4 «Приближённое вычисление иррациональных чисел», c. 112—117].
Клюкин И. И. Удивительный мир звука. — Л.: Судостроение, 1986.
Брэгг У. Мир света. Мир звука. — М.: Наука, 1967.
Логарифмическая линейка