Катафот известен всем с детства — его устанавливают на спицах колёс велосипеда.
Катафоты играют важную роль в повышении безопасности дорожного движения. В отличие от фар, катафот не требует энергии и не содержит лампочек. Но если его закрепить на велосипеде, мотоцикле, автомобиле, если превратить в катафот с помощью специального покрытия даже небольшую часть куртки пешехода или поверхность дорожного знака, — во всех этих случаях водитель машины, фары которой осветили один из перечисленных объектов, сразу его заметит из-за отражения света фар от катафота.
Простейшая разновидность катафота — уголковый отражатель, именно его мы видим на велосипедах и автомобилях. Для объяснения принципов работы уголкового отражателя достаточно школьных знаний из оптики и геометрии.
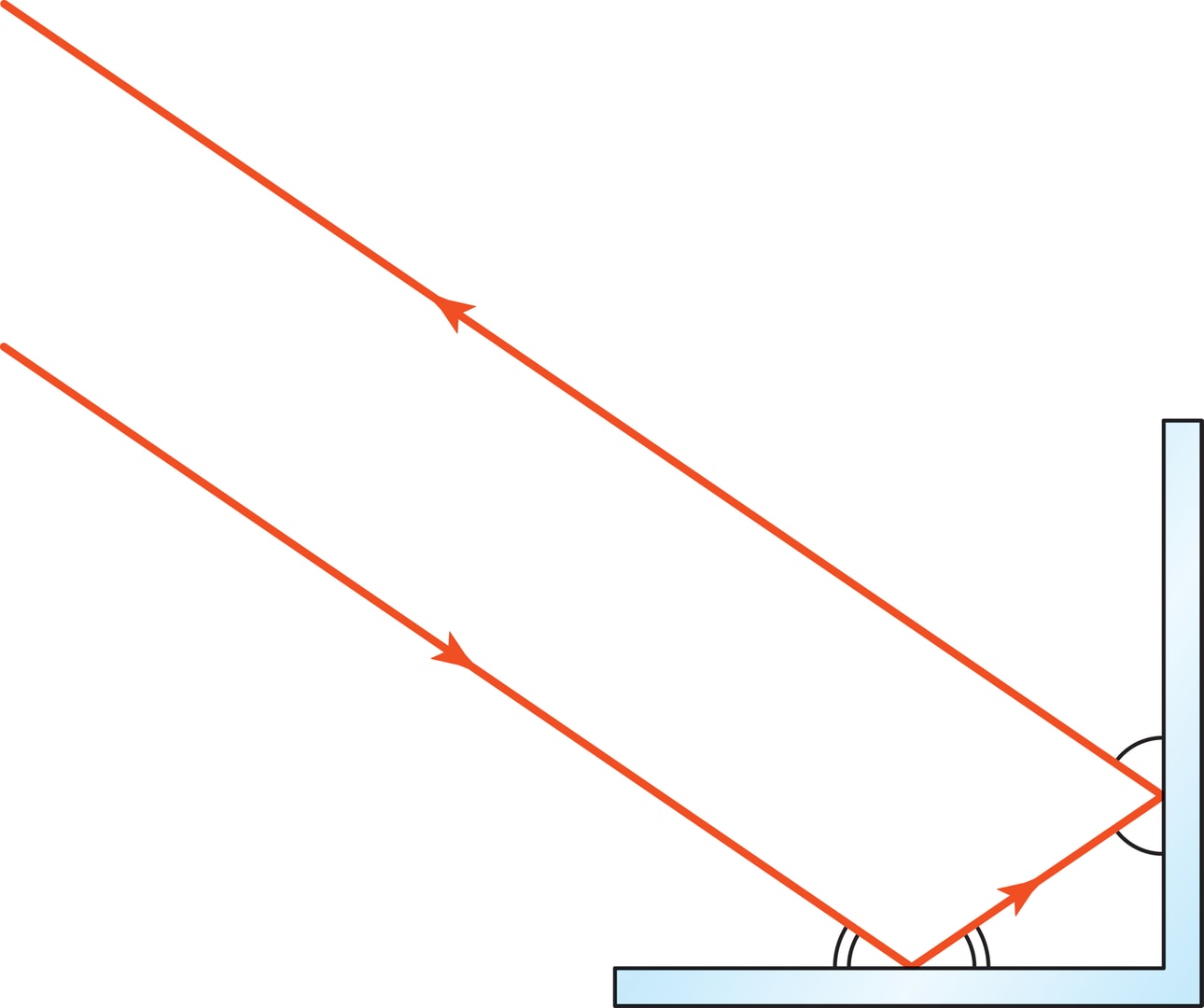
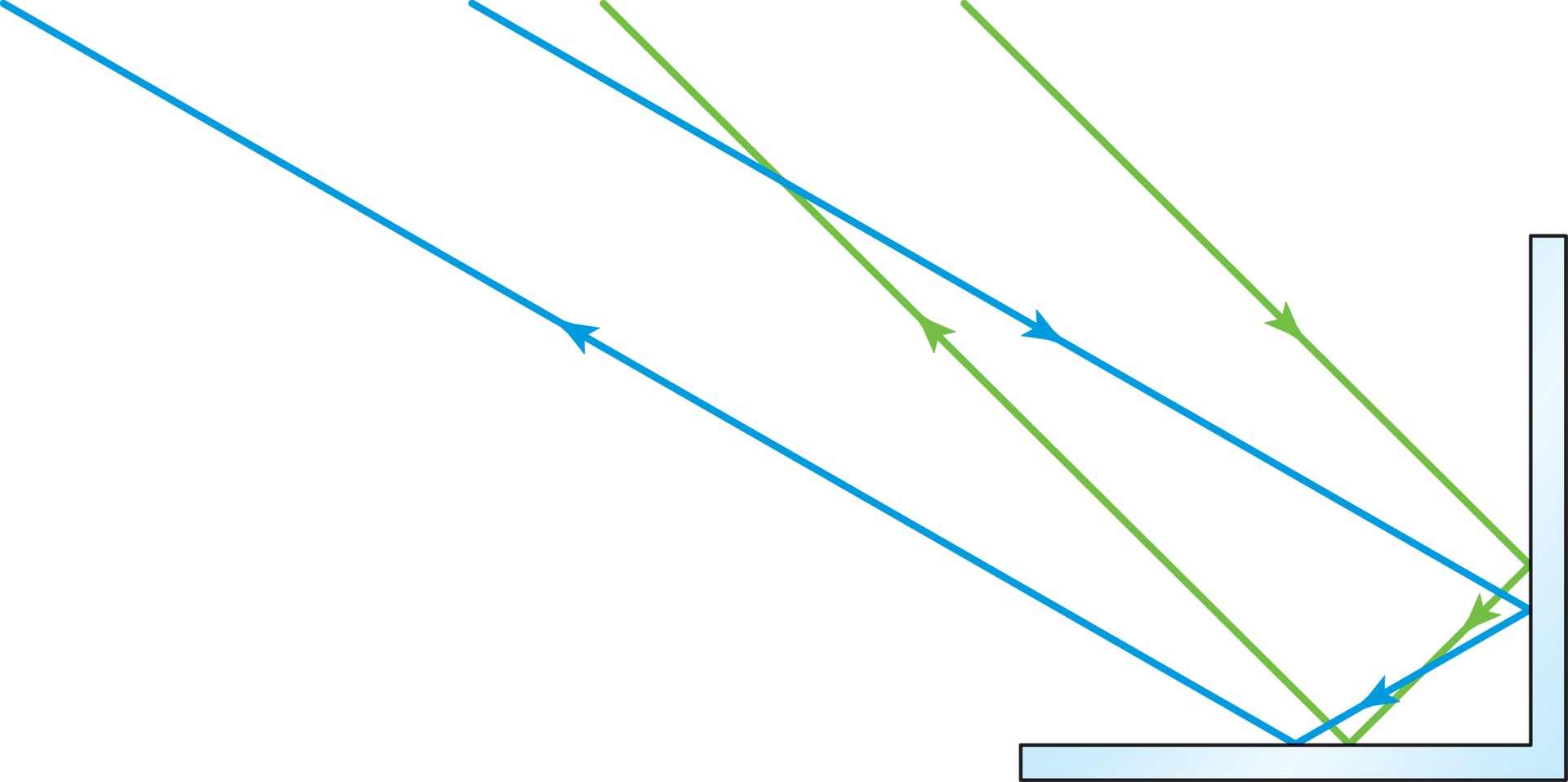
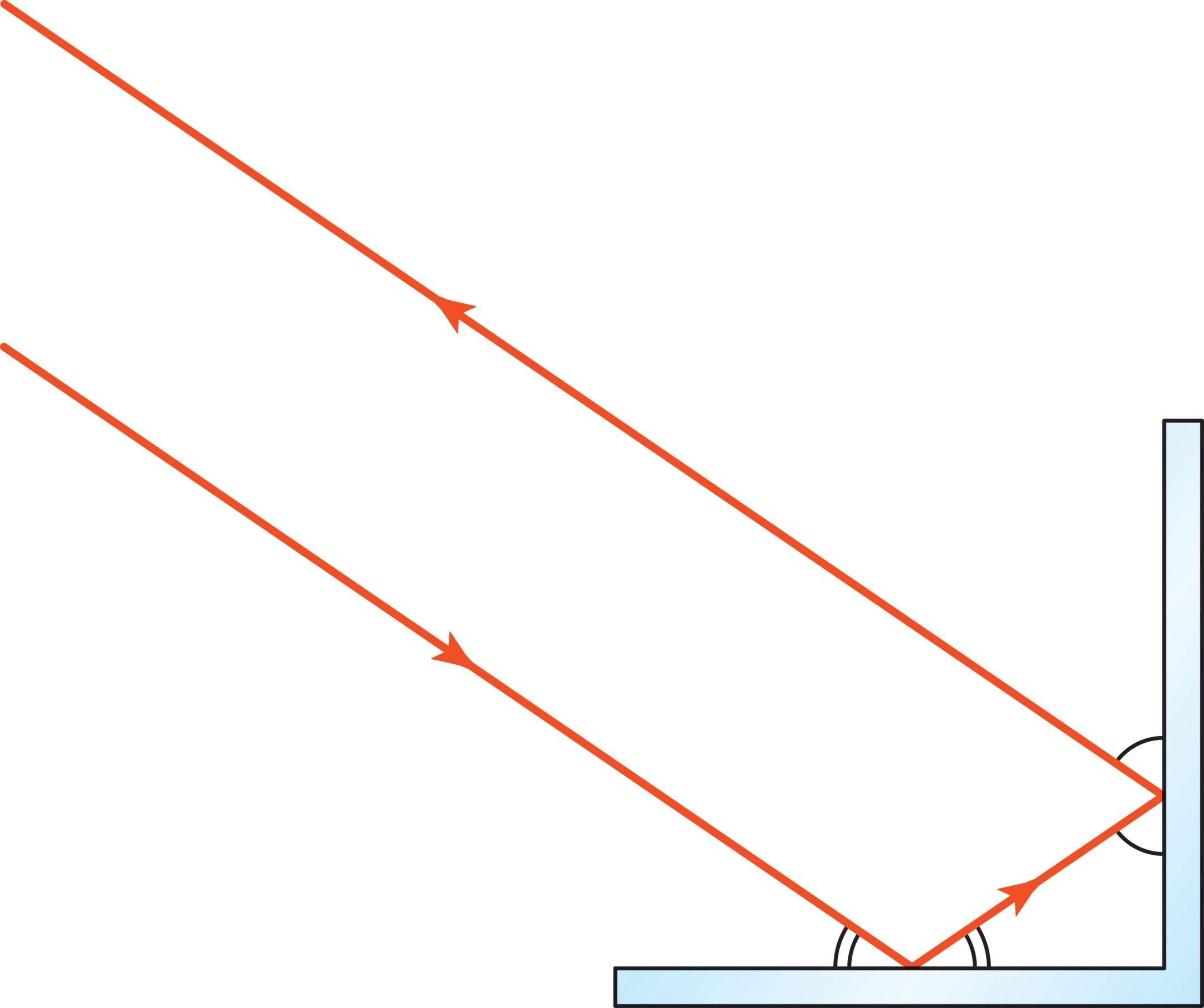
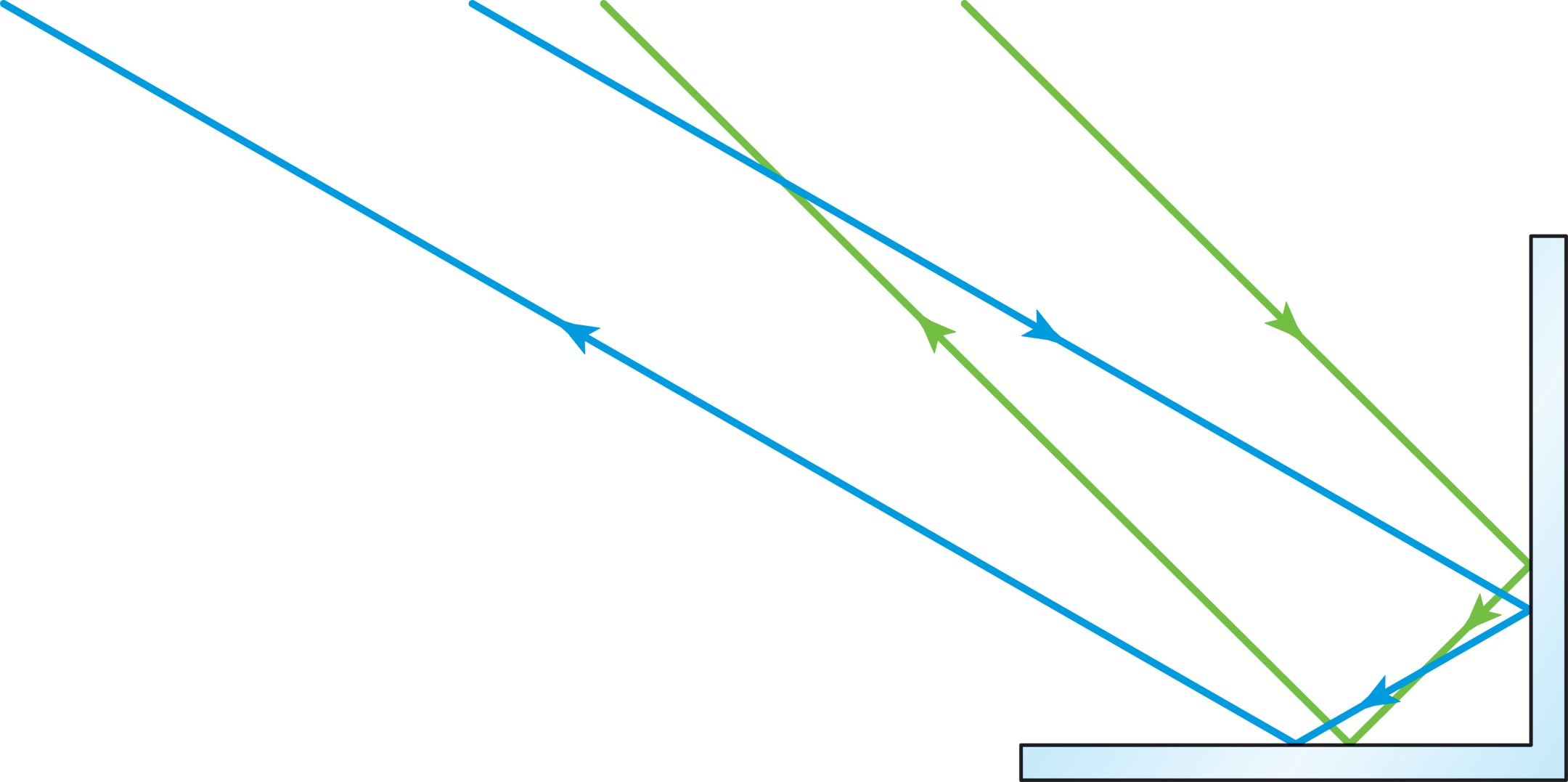
Возьмём в плоскости два перпендикулярных «зеркальных» отрезка, от которых луч отражается по закону «угол падения равен углу отражения». Отразившись последовательно от обоих зеркал, луч уйдёт в сторону источника параллельно исходному лучу. Для доказательства сформулированного утверждения достаточно вспомнить и применить два геометрических факта: 1) сумма углов в треугольнике равна 180°, 2) признак параллельности прямых (сумма внутренних односторонних углов при секущей равна 180°).
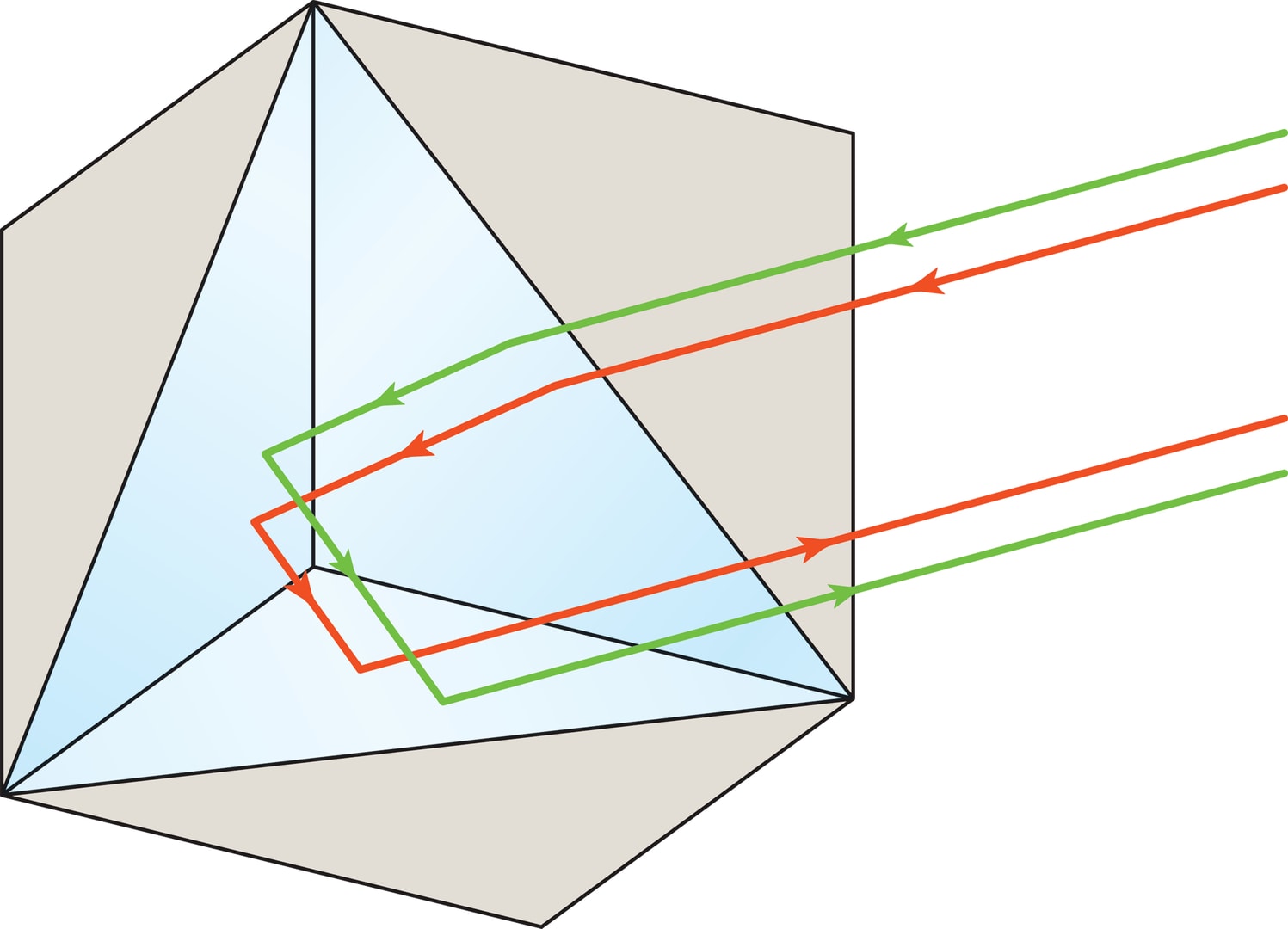
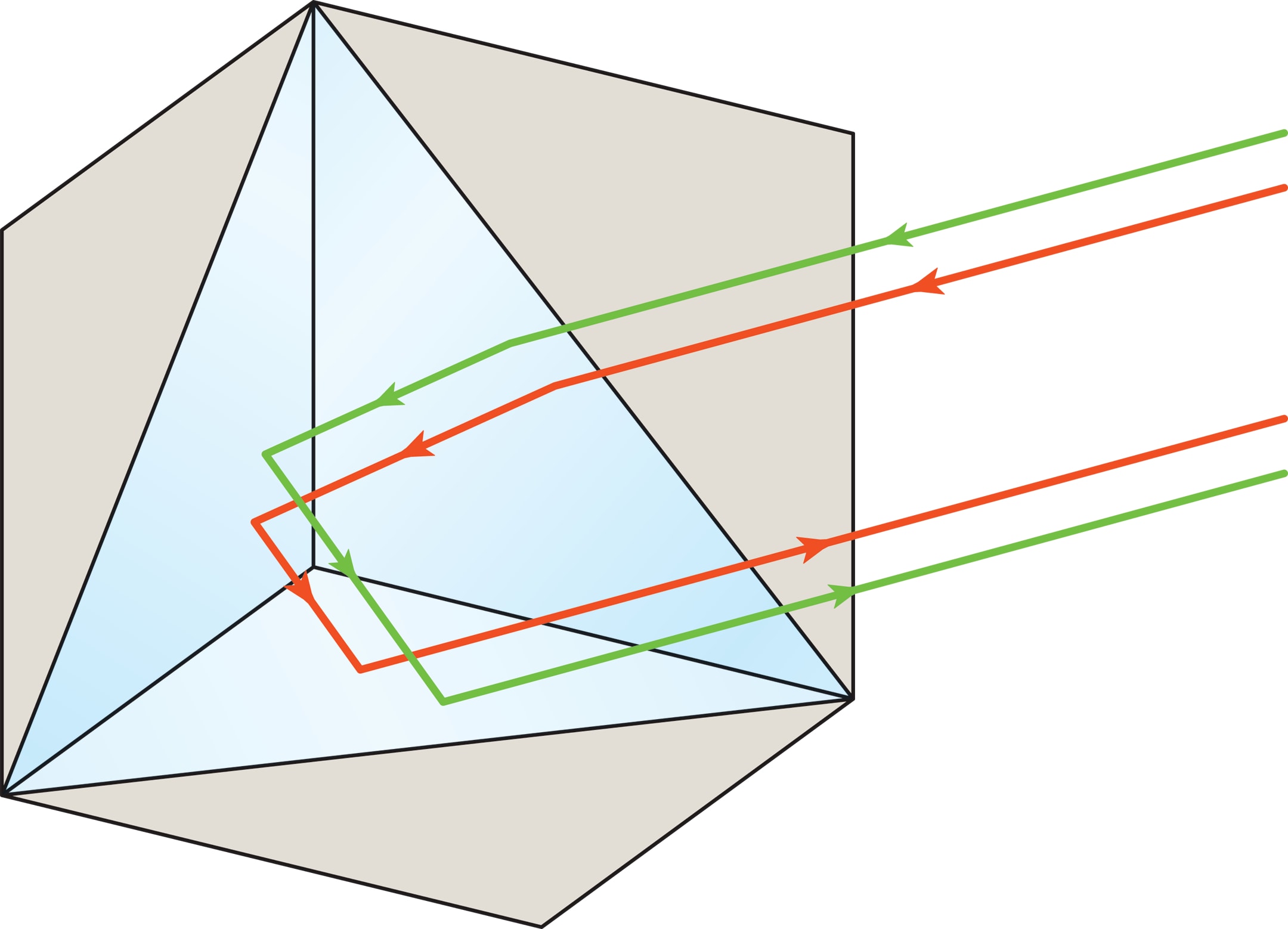
Чтобы получить такой эффект в нашем (трёхмерном) пространстве, нужно взять три взаимно перпендикулярных зеркала.
В этом случае «экономное» объяснение эффекта можно дать на языке векторов. Если направление исходного луча задаётся вектором с координатами ($a$; $b$; $c$), то после отражения луча от плоскости $xOy$ его направляющим вектором будет ($a$; $b$; $-c$), а после последовательных отражений от плоскостей $yOz$ и $zOx$ — ($-a$; $b$; $-c$) и ($-a$; $-b$; $-c$) соответственно. Конечно же, подобное объяснение можно привести и для плоского случая.
Катафот данного типа представляет собой множество уголков-ячеек, что обеспечивает увеличение «отражательной силы» устройства. Для создания ячеистого зеркала важно то, что равными (и в частности равносторонними) треугольниками можно замостить плоскость.
Вернёмся к автомобилям — свет включённых фар, отразившись от катафота, «вернётся» к водителю машины, сообщая ему об объекте, находящемся впереди.
Катафоты верно служат и в других средах, например, их можно встретить на морях и реках: они являются частью оснастки небольших яхт и плотов; буй, определяющий границы участков и водные пути, с закреплённым на нём катафотом, становится источником важных сигналов.
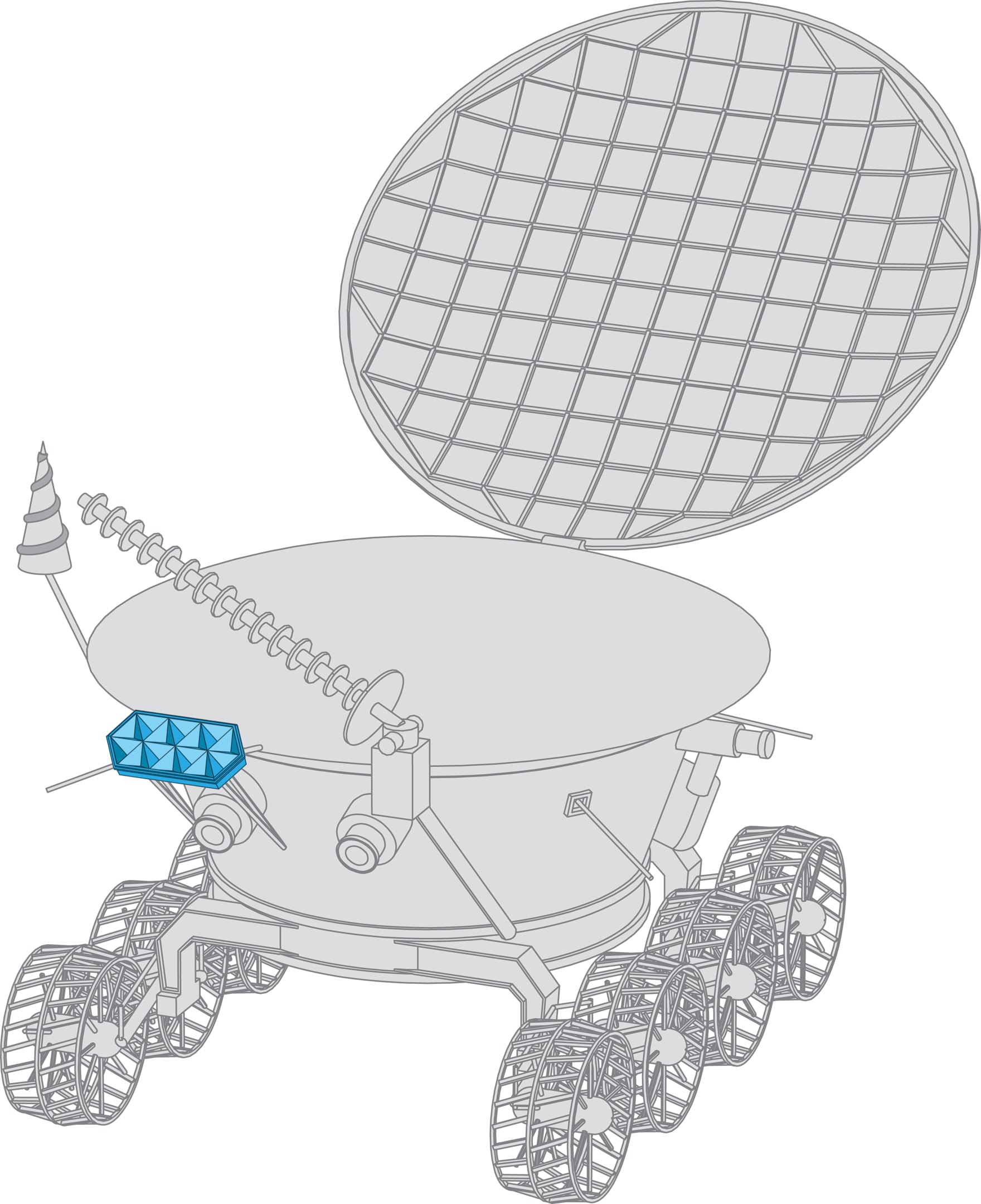
Ещё один пример — из истории освоения космоса. Для исследования Луны в Советском Союзе была разработана серия аппаратов «Луноход». Первый аппарат «Луноход‐1» был доставлен на поверхность Луны 17 ноября 1970 года, «Луноход‐2» — в январе 1973 года. На обоих луноходах были установлены уголковые отражатели. Эти отражатели, а также отражатели американской программы «Аполлон» позволяют с большой точностью измерять постоянно меняющееся расстояние от Земли до Луны. А эта характеристика «межпланетных отношений» важна и в чисто земной жизни, например, в учёте влияния приливов и отливов, и в чисто космической, например, при расчёте траекторий космических аппаратов.
В некоторые светоотражающие покрытия, например, на дорожных и автомобильных номерных знаках, на одежде, «встроен» другой тип катафота. Эти покрытия содержат мелкие шарики, проникая в которые свет отражается от «задней стенки» шарика, а затем выходит из него наружу параллельно тому направлению, откуда пришёл. По сути маршрут аналогичен тому, который проходит световой луч в капле дождя при возникновении радуги (см. «Радуга»), с той лишь разницей, что из водяной капли свет выходит под углом в $41°$—$42°$ к приходящему солнечному, а в катафоте — параллельно исходному направлению.
Интересные впечатления дарит уголковый отражатель, сделанный из трёх относительно больших зеркал. Если, перемещаясь, смотреть на модель, то можно обнаружить, что отражение следит за вами. А если, стоя перед отражателем, по очереди закрывать глаза, то обнаружится, что каждый раз отражение открытого глаза смотрит прямо на вас и всегда из перекрестья плоскостей зеркал.