Различающиеся по назначению изделия — вёдра из жести и стаканчики для напитков, бумажные или пластиковые — имеют одинаковую форму: это усечённые конусы. Приглядевшись, замечаем ещё одну общую черту: верхняя кромка отогнута наружу и образует круглую закраину.
Почему же и для вёдер, и для стаканчиков выбрана именно такая конструкция? Попробуем разобраться.
Первое, на что стоит обратить внимание, — это простота изготовления цилиндра или конуса.
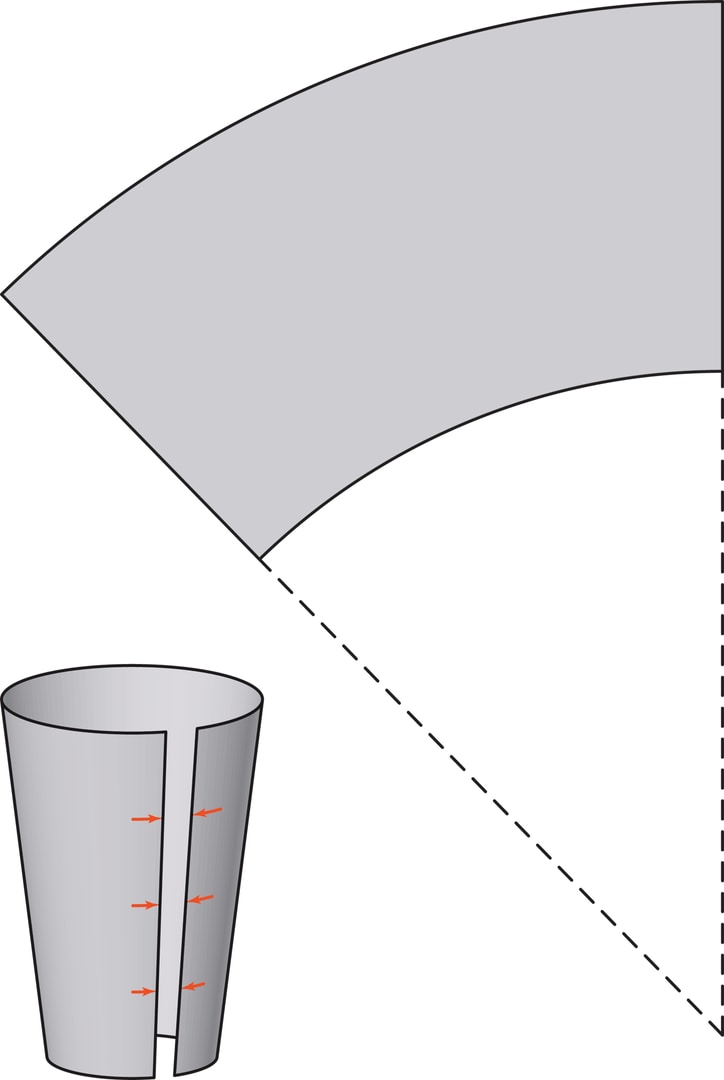
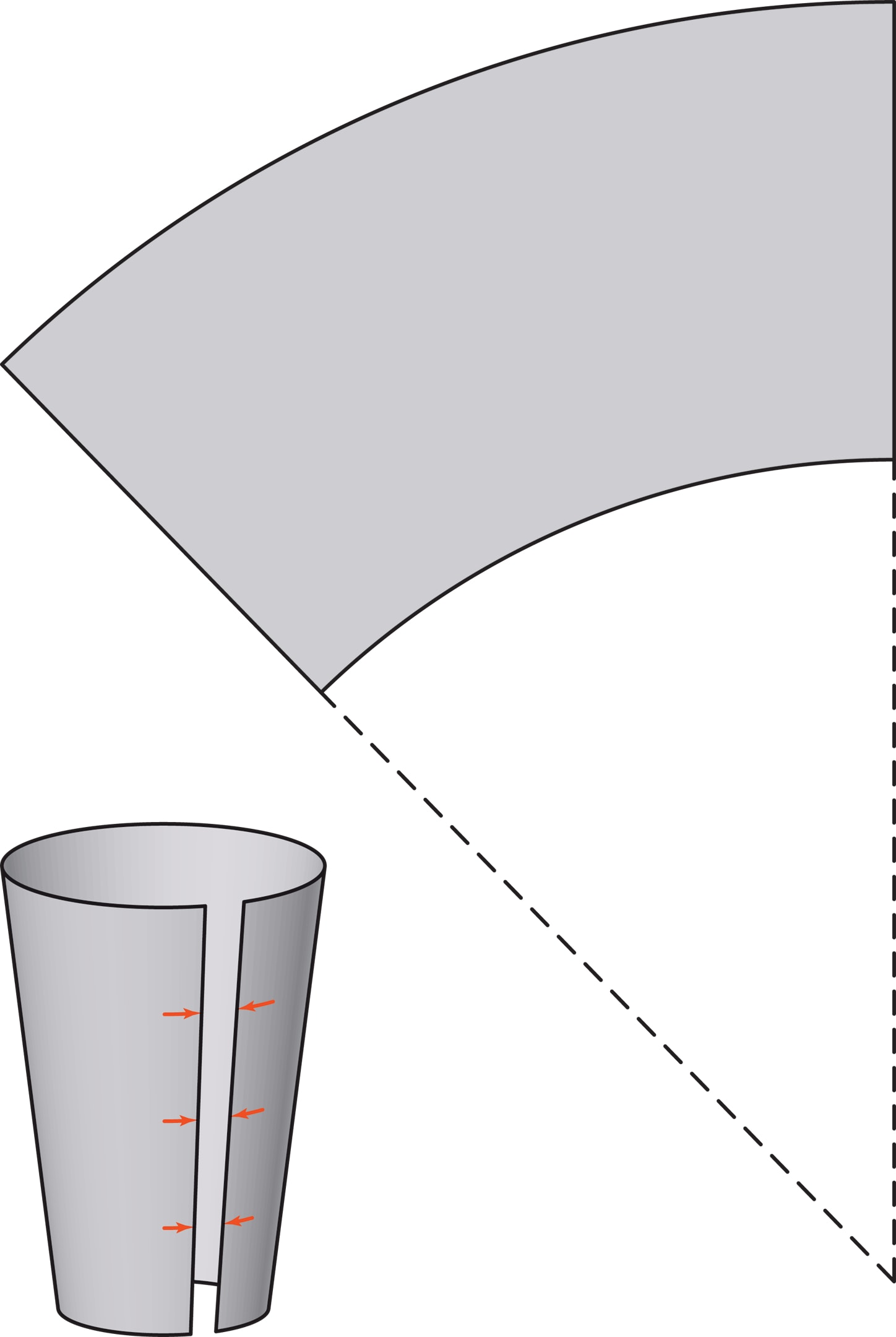
Заготовка в виде плоского листа прямоугольной формы — развёртка боковой поверхности цилиндра, а сектор круга сворачивается в боковую поверхность конуса. А развёртка усечённого конуса — «усечённый сектор»: сектор круга, от которого отрезали сектор меньшего радиуса. Свернув лист выбранной формы (с добавленными припусками на швы), получаем боковую поверхность будущего ведра или стаканчика, остаётся приделать дно и обеспечить водонепроницаемость швов.
Технология не меняется, если дно — не круг, а вытянутый овал или какая‐то иная фигура. Дело в том, что помимо прямого кругового цилиндра и прямого кругового конуса можно определить и более широкий класс цилиндрических и конических поверхностей, «опирающихся» на выбранную кривую (границу дна). Их также можно изготавливать из плоских развёрток. Ценность описанных конструкций увеличивает то, что из плоских развёрток простым сворачиванием ничего, кроме цилиндров и конусов, получить не удастся.
Но если сложность изготовления цилиндрических и конических вёдер примерно одинакова, а в повседневности конические изделия имеют подавляющее численное преимущество, то возникает вопрос: чем это объясняется?
Главное преимущество конической формы — изделия, сделанные на основе одинаковых заготовок-развёрток боковых поверхностей, можно вкладывать друг в друга, что важно и при хранении, и при перевозке. Причём прямой круговой конус — поверхность вращения, поэтому можно складывать изделия стопкой, «вслепую», не заботясь об их совместимости.
В наши дни жестяные изделия почти полностью вытеснены штампованными изделиями из пластика. Теперь не нужно изгибать плоские жестяные листы, пластмассовое изделие изготавливается целиком. В результате чаще стали встречаться вёдра, дно которых — квадрат, прямоугольник, эллипс или ещё более причудливая фигура. Но боковые поверхности — по‐прежнему конические, и в магазине покупатели видят привычные стопки из вложенных друг в друга однотипных вёдер.
Как у жестяных и бумажных изделий, так и у их пластиковых двойников есть ещё одна общая черта, о которой уже говорилось, — загнутая верхняя кромка, закраина. Чтобы понять роль закраины, проведите эксперимент. Возьмите одноразовый пластиковый стаканчик для холодных напитков (кулер и стопки таких стаканчиков — почти обязательная деталь в современных офисах) и попробуйте сдавить его с боков. Вы ощутите сопротивление стаканчика, он «не захочет» уплощаться. Отрежьте теперь верхнюю часть с закраиной и снова сдавите стенки — вы увидите, что лишённая жёсткой рамки-закраины верхняя половина стаканчика будет сжата беспрепятственно.
Дело в том, что коническая поверхность — непрерывно изгибаемая. На «языке» стаканчика это свойство означает следующее. Во‐первых, его стенку, сделанную из гибкого, тонкого пластика, можно деформировать. Во‐вторых, нерастяжимость пластика обеспечивает в процессе изгибания неизменность длины любой линии, нарисованной фломастером на поверхности.
А вот закраина из такого же материала, но имеющая форму круглого жёлоба, не допускает непрерывных изгибаний. Более точно, неизгибаемым является как весь тор — поверхность бублика, так и любой вырезанный из него кольцевой жёлоб, даже мелкий.
В завершение эксперимента со стаканчиком, положите его отрезанную верхнюю часть на стол загнутой кромкой вниз и попробуйте сжать закраину, не отрывая от поверхности стола. Вам будет казаться, что пальцы сжимают жёсткую мощную пружину.
Кольцеобразные пояса жёсткости, «вырезанные» из тора, используются и при изготовлении банок для напитков. Материал — очень тонкий металл, поэтому и крышка банки, и её дно переходят в боковую поверхность через «арматурные пояса», каждый состоит из пары соединённых «разновыпуклых» четвертинок тора.
Приведём критерий того, что полоска поверхности вращения являтся жёсткой — не допускает непрерывного изгибания.
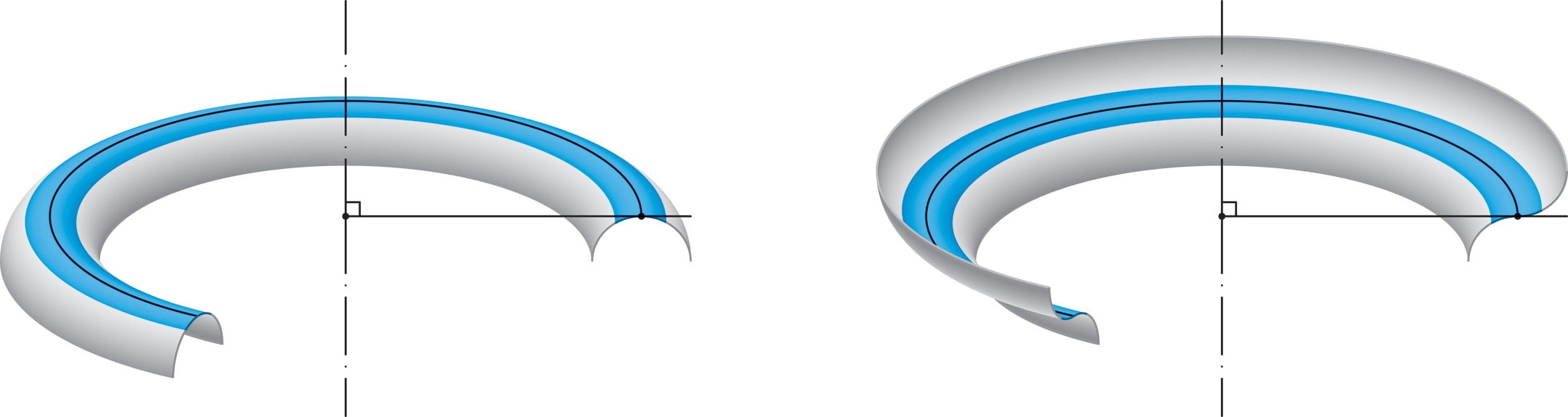
Тор (поверхность бублика) можно представлять как результат вращения вокруг вертикальной оси небольшой окружности, находящейся в одной плоскости с осью на некотором расстоянии от неё.
Если вращать только верхнюю половинку окружности, то получится закраина питьевого стаканчика (желобок) — жёсткая поверхность, не допускающая непрерывного изгибания. А если вращать дугу, касательные к которой ни в одной точке не перпендикулярны оси вращения, то получится изгибаемая поверхность.
Наличие касательной, перпендикулярной оси, — критерий жёсткости поверхности вращения, какой бы узкой она ни была. Причём можно рассматривать и более сложный, не обязательно «круговой» профиль. Дуги кривой (не обязательно окружности) могут подходить с разных сторон к перпендикулярной касательной, поверхность всё равно получится жёсткой. Такие пояса жёсткости есть в верхней и нижней частях любой алюминиевой банки для напитков.
Ещё со школьной скамьи многие знают фамилию Алексея Васильевича Погорелова — автора одного из школьных учебников геометрии. Алексей Васильевич был академиком Академии наук СССР, область его научных интересов — внешняя и внутренняя геометрия поверхностей, теория упругих оболочек. По теории изгибаемых поверхностей А. В. Погорелов написал несколько монографий: «Изгибание поверхностей и устойчивость оболочек», «Внешняя геометрия выпуклых поверхностей», «Геометрическая теория устойчивости оболочек».
Александров А. Д. Кривые и поверхности
Фоменко В. Т. Изгибание поверхностей