С древних времён для украшения изделий или зданий люди использовали орнаменты — плоские узоры, составленные из небольшого набора одинаковых элементов и отличающиеся геометрической правильностью, повторяемостью рисунка. Собственно, латинское слово ornamentum и означает «украшение». И зрительное восприятие, и математическая классификация выделяют два типа плоских узоров.
Бордюр — это полоска, внутренняя каёмка на краю предмета. Бордюрные узоры могут украшать одежду, книжную страницу, обрамлять фреску в настенной живописи, стену или потолок. В античной Греции бордюры как украшения можно было встретить повсюду: от горлышка вазы до фриза (полоса в верхней части здания). Для часто встречавшихся рисунков, состоявших из изломов прямых линий, греки даже ввели отдельное название — меандр, в честь одноимённой извилистой реки.
Орнаменты плоские, в отличие от бордюров-полос, занимают не край полотна или стены, а всё выделенное поле. В исламской архитектуре орнаменты — главная часть декора, знаменитые примеры — исторические памятники Самарканда, отделка дворцов Альгамбры, построенных в Испании во времена мавританского владычества.
Если отвлечься от художественной стороны узоров, весь разнообразный и многоликий мир орнаментов можно классифицировать в зависимости от того, как выглядит группа, набор движений, переводящих данный орнамент в себя. Можно взглянуть на эту классификацию и с точки зрения динамики: выяснить, как выглядят преобразования, с помощью которых из небольшой ячейки «восстанавливается» весь орнамент. Оказывается, классификационных типов немного: бесконечных бордюров — 7 типов, бесконечных плоских орнаментов — 17 типов.
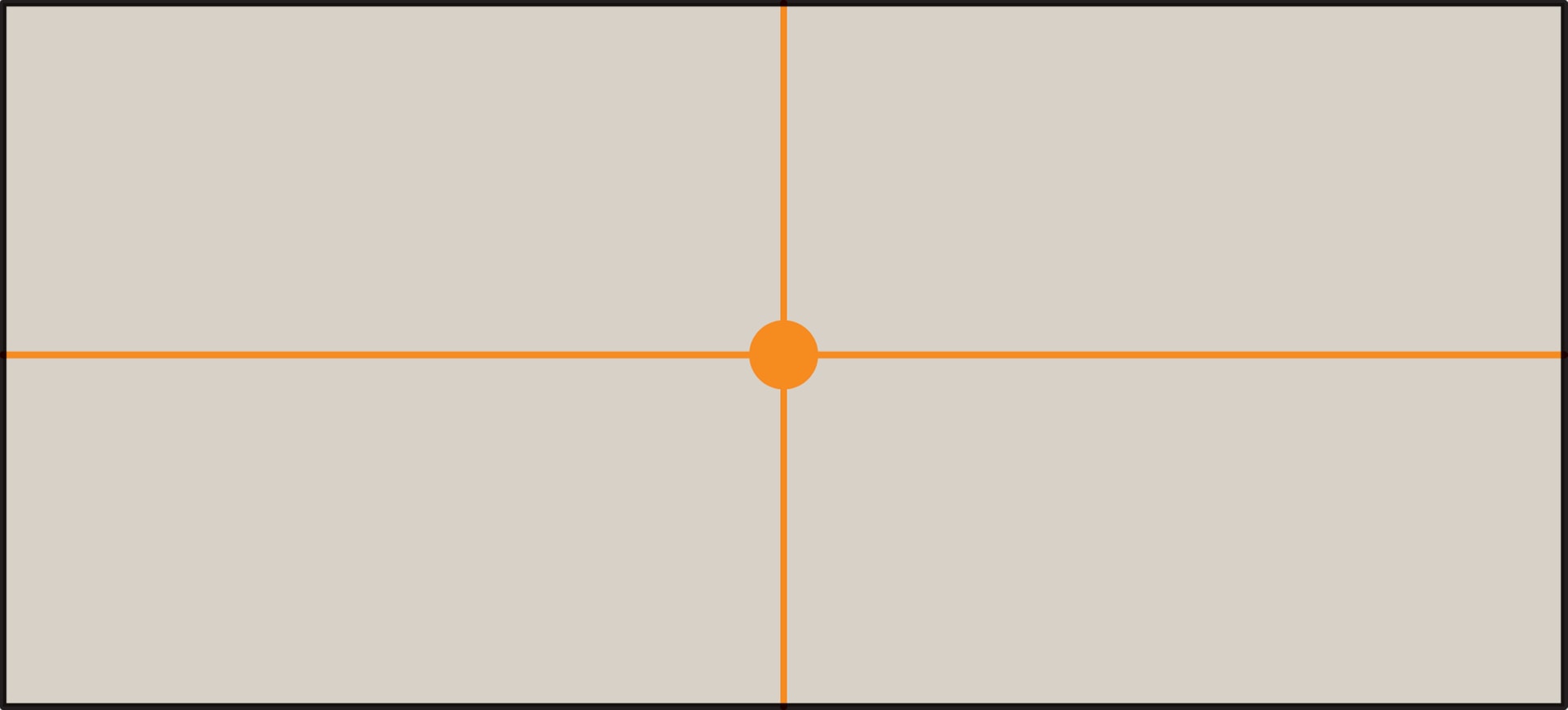
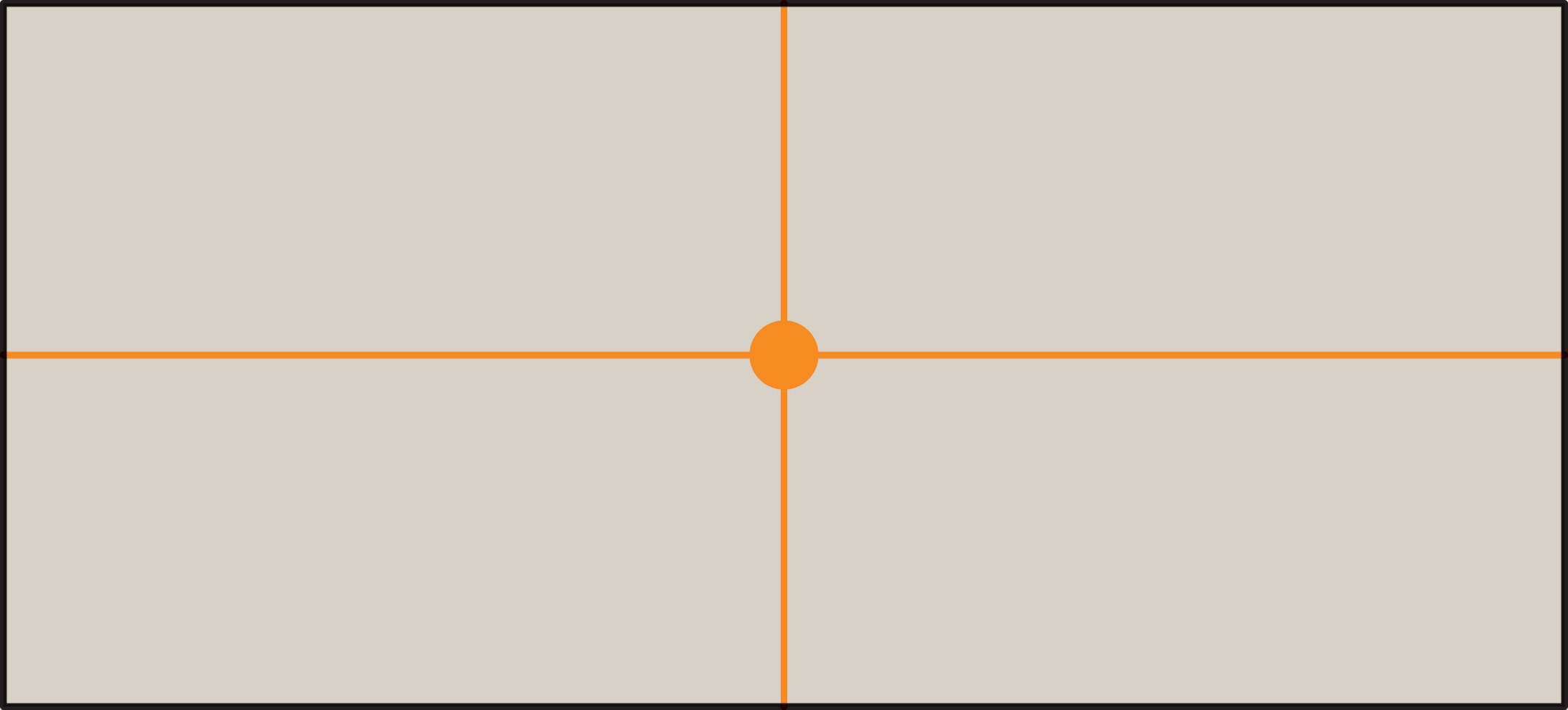
Начнём разговор о классификации с простого, но содержательного примера — прямоугольника. Эта геометрическая фигура обладает двумя осевыми симметриями: $H$ — симметрия относительно горизонтальной прямой, проходящей через центр; $V$ — вертикальной. Ещё имеется центральная симметрия, обозначим её через $R$, поскольку она совпадает с поворотом вокруг центра на $180°$. Другими симметриями прямоугольник не обладает. Доказательство основано на том, что для любой конечной фигуры (в том числе для прямоугольника) при движении, совмещающем её с собой, центр тяжести фигуры переходит в себя. Значит, движение может быть или поворотом около центра, или симметрией относительно прямой, проходящей через центр. Можно и экспериментально «убедиться», что кроме $H$ и $V$ нет других осевых симметрий (попробуйте, например, складывая прямоугольный лист по диагонали), а единственный нетривиальный поворот — на угол $180°$.
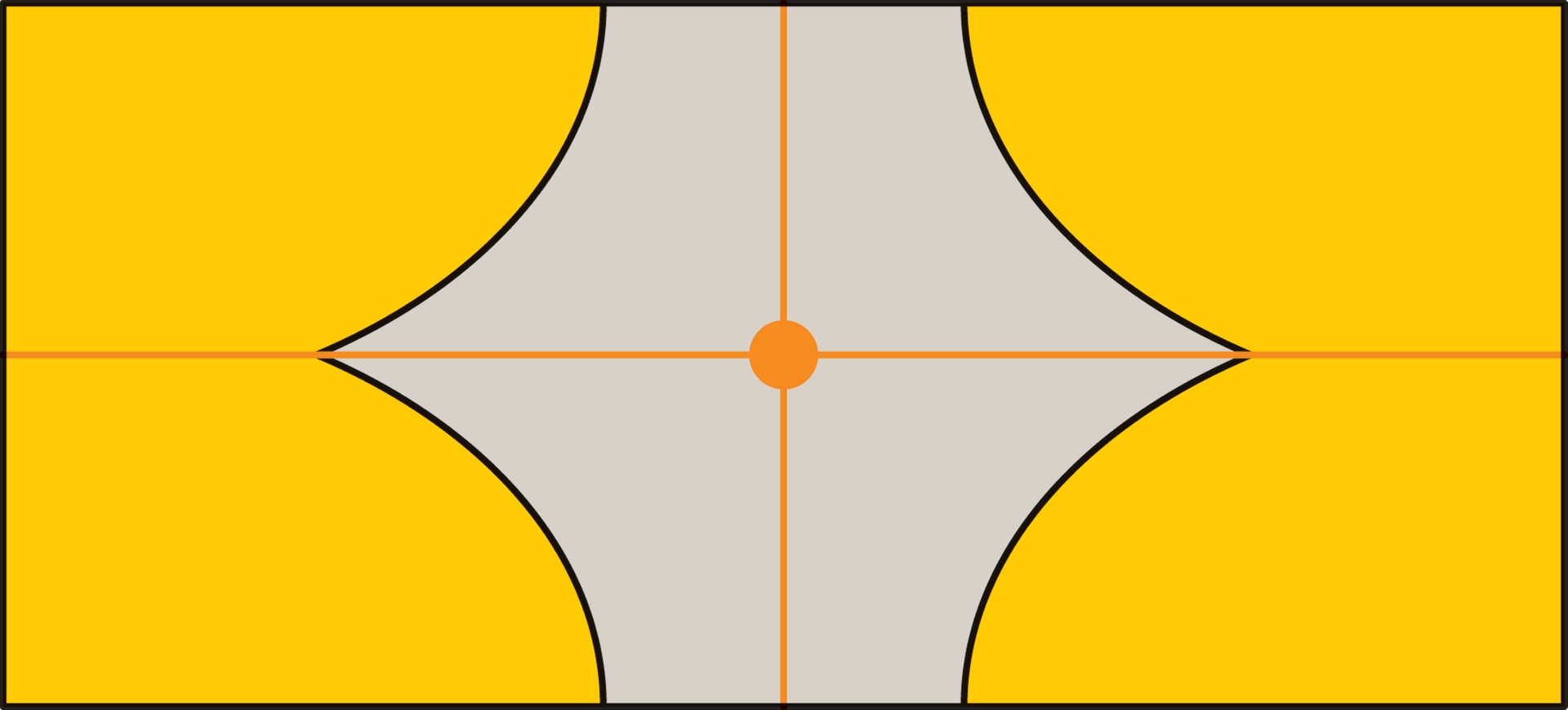
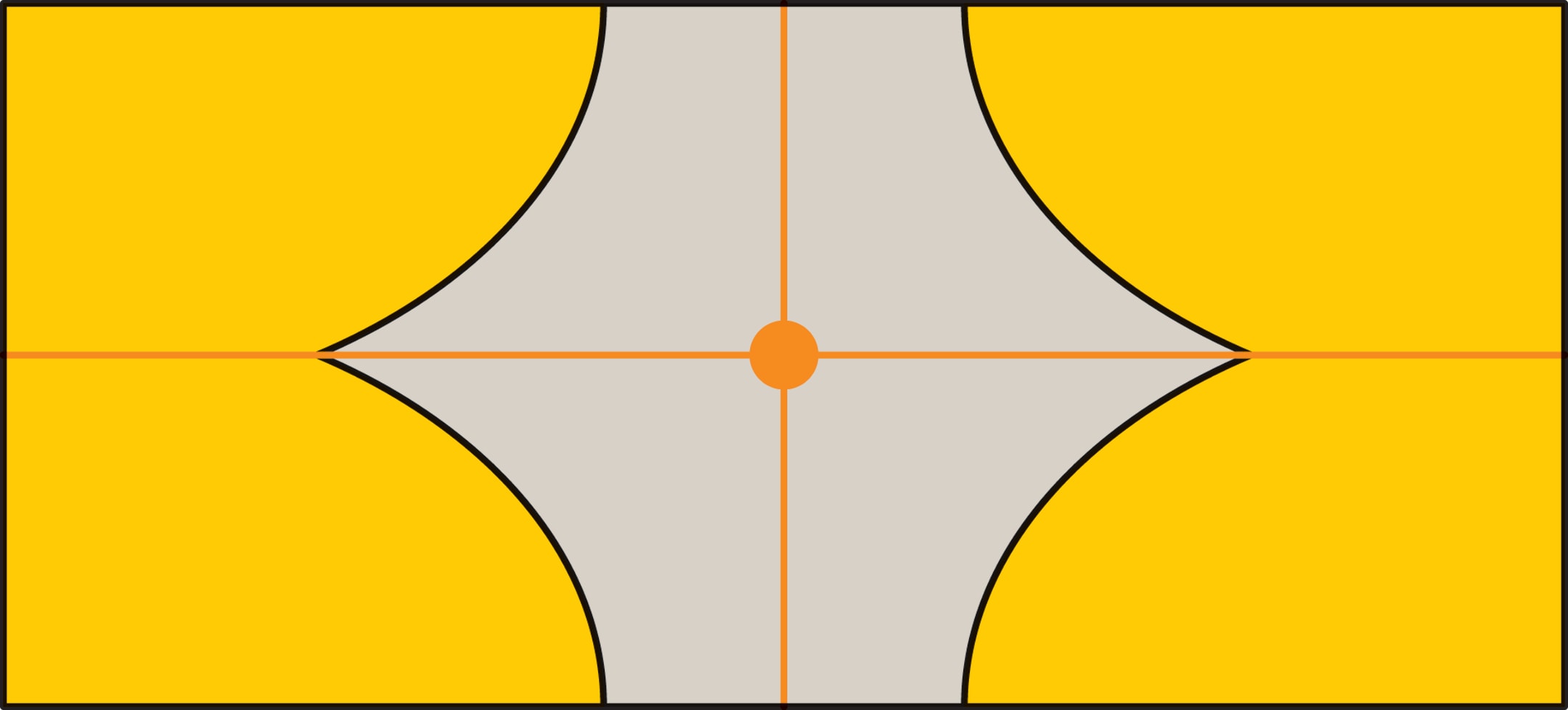
А какие симметрии бывают у раскрашенного прямоугольника? Симметрии такого прямоугольника надо искать только среди набора $\{H, V, R\}$, поскольку прямоугольник в любом случае должен перейти в себя. Чтобы последующее получило наглядное представление, будем одинаково закрашивать углы прямоугольника. Если закрашен только один угол, то такой прямоугольник не обладает ни одной из симметрий $H$, $V$ или $R$. Если закрашены два угла, то, в зависимости от сочетания углов, имеется только одна из базовых симметрий $H$, $V$ или $R$.
Любопытно, что прямоугольного узора ровно с двумя симметриями не может быть. Перемещения закрашенного угла под действием симметрий помогают увидеть, что $VH=R$, $RV=H$, $HR=V$ — последовательное выполнение двух симметрий (в любом порядке) даёт третью. Таким образом, если у прямоугольного узора имеются две симметрии, то имеется и третья. Пример: прямоугольник с четырьмя одинаково закрашенными углами.
Итак, в зависимости от числа симметрий, которыми обладают прямоугольные узоры, они делятся на пять типов: несимметричные, с одной симметрией (из набора $H$, $V$, $R$), с тремя симметриями.
Набор движений, переводящих раскрашенный прямоугольник в себя, является группой. Движение плоскости — это преобразование, сохраняющее все расстояния. Примеры: параллельный перенос, симметрия, поворот. Группой в математике называется множество, на котором определена операция (условно называемая умножением) такая, что: «произведение» двух элементов группы — тоже элемент группы; есть «единица» — нейтральный элемент относительно умножения; у каждого элемента есть обратный, умножение на который даёт единицу. Для движений плоскости умножение — это их композиция, т. е. последовательное выполнение; единицей является тождественное преобразование $I$; обратный элемент — обратное преобразование. В случае прямоугольника число элементов группы зависит от раскраски, наибольшая возможная группа состоит из четырёх элементов — $\{I, H, V, R\}$.
Бордюр — повторяющийся (периодический) узор, бесконечно продолжаемый, заключённый между двумя параллельными прямыми. Все такие узоры можно построить, если к согласованным с прямыми границами бордюра симметриям вида $H$, $V$ и $R$ добавить ещё два вида движений: параллельные переносы $T$ вдоль границ и скользящие симметрии $G$ — композиции горизонтальной симметрии и параллельного переноса $(G=HT)$.
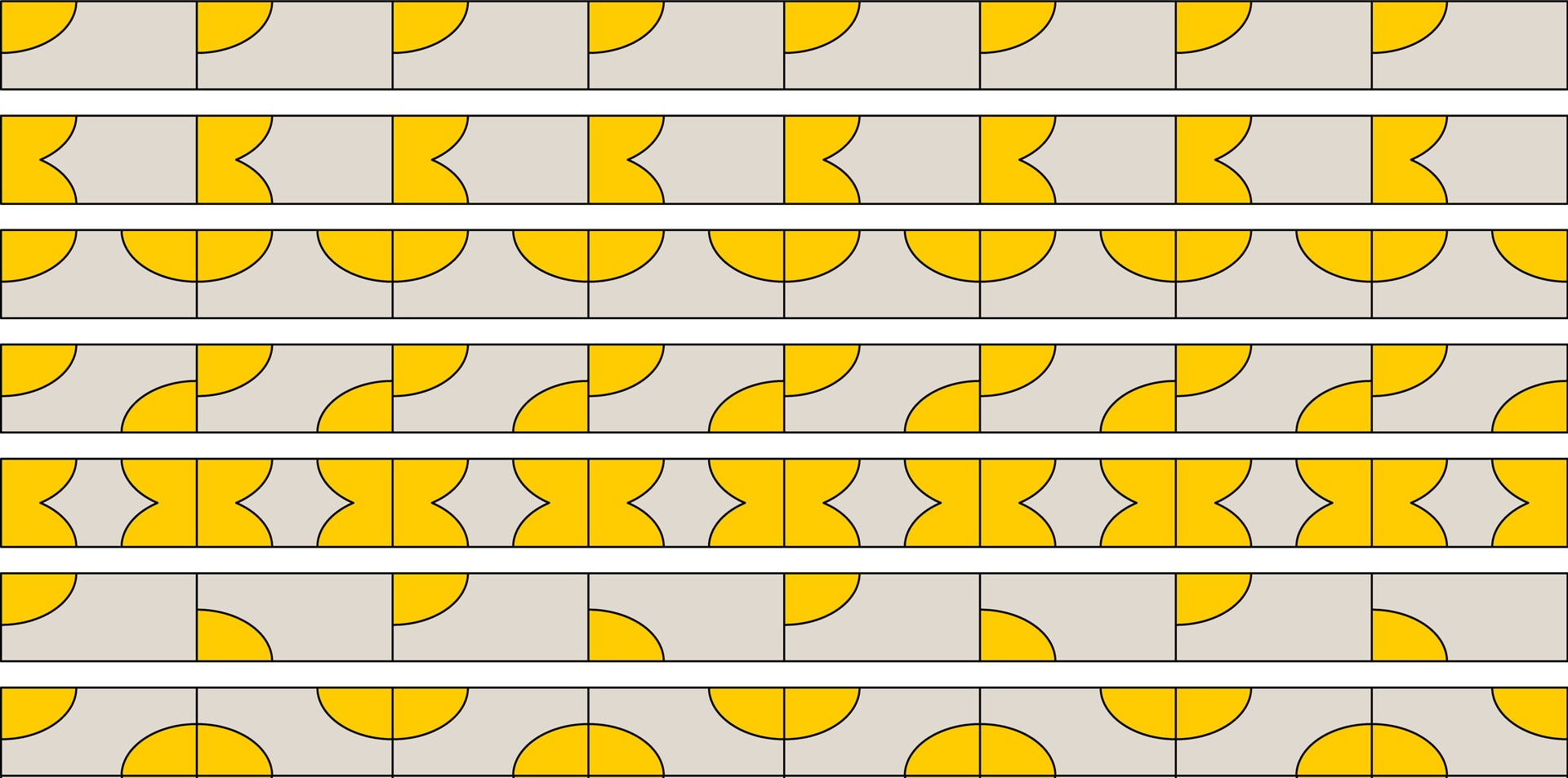
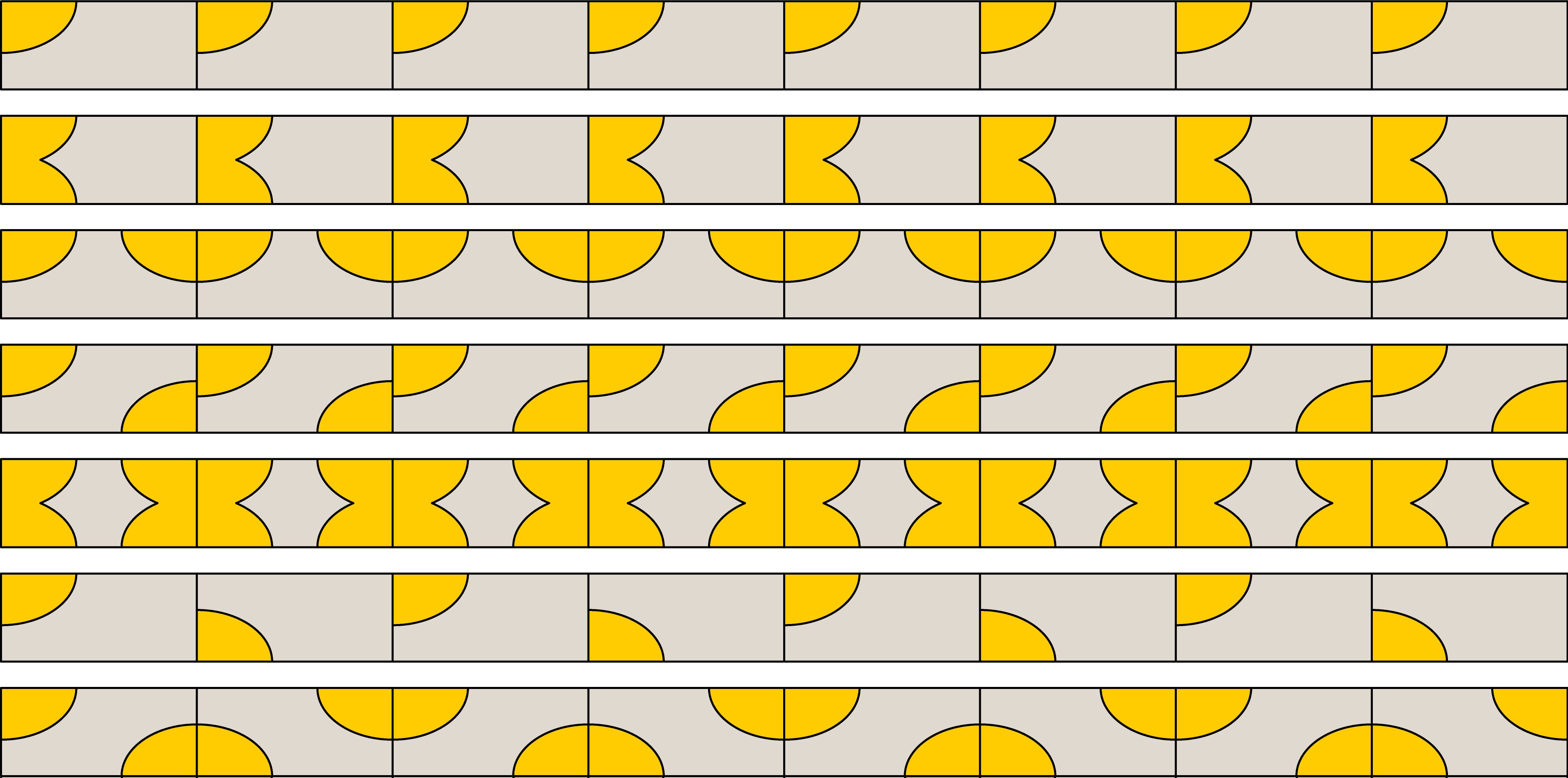
Семь возможных типов периодических бордюрных узоров следующие. Бордюры первых пяти типов получаются параллельным переносом рассмотренных прямоугольных узоров (одинаково раскрашенные прямоугольники приставлены друг к другу, образуя бесконечную в обе стороны ленту). Ещё два типа — результат применения скользящей симметрии к несимметричным прямоугольным узорам (прямоугольники с одним закрашенным углом) и к прямоугольникам с одинаково закрашенными противоположными углами.
Других типов периодических бордюров нет. Доказательство основано на анализе группы движений бордюрного узора, элементами которой могут быть горизонтальная симметрия $H$ и представители семейств $V$, $R$, $T$ и $G$. Несложно проверить, что композиция перечисленных видов даёт движение из этого набора, например, композиция вертикальной симметрии и скользящей симметрии — центральная симметрия. Но, в отличие от случая прямоугольника, теперь порядок проведения преобразований важен, например, композиция двух вертикальных симметрий в разных порядках даёт параллельные переносы, но в противоположных направлениях.
Ещё одно замечание: как и в группе $\{I, H, V, R\}$, преобразования в наборе $\{H, V, R, T, G\}$ не независимы. Например, скользящая симметрия по определению — композиция $HT$. Это приводит к различным способам описания конкретного бордюра. Так, бордюр пятого типа можно двумя способами получить из прямоугольного узора с тремя симметриями (четыре закрашенных угла в прямоугольнике): параллельным переносом и скользящей симметрией. Этот же бордюр можно получить даже из половинки прямоугольника с помощью вертикальных симметрий. А бордюр седьмого типа тоже можно построить не скользящей симметрией прямоугольника, а вертикальными симметриями.
Наличие параллельных переносов в группе движений бордюра необходимо. Из четырёх других видов преобразований ($H$, $V$, $R$ и $G$), в принципе, в группе может не быть ни одного, могут присутствовать только один, только два или только три (в разных сочетаниях), все четыре. Формально получается $16=2^4$ возможных вариантов, но реализуются они не все. Ситуация сходна с приведённым ранее объяснением того, что не бывает прямоугольного узора ровно с двумя симметриями. Например, в случае бордюра не могут входить в группу только симметрии вида $H$ и вида $V$, поскольку тогда в группу входило бы и их произведение, симметрия $R=HV$.
И хотя имеется всего 7 типов периодических бордюров, внутри исходного прямоугольника можно выбирать узор произвольно, а значит, и запас красивых бордюрных узоров неисчерпаем.
Бесконечный плоский периодический орнамент обладает двумя чертами. Во‐первых, его правильность имеет математическую формализацию — движения, переводящие орнамент в себя, образуют группу. Во‐вторых, весь орнамент можно построить с помощью этих движений из какого‐то небольшого его фрагмента (ячейки). Исходя из этого, можно описать все возможные группы движений орнамента.
Традиционно движения плоскости распределяются по видам $\{S, R, T, G\}$: $S$ — симметрии относительно прямых, $R$ — повороты, $T$ — параллельные переносы, $G$ — скользящие симметрии. Оказывается, в группе движений орнамента должны быть переносы по непараллельным направлениям (как минимум двум), а повороты возможны только на углы вида $360°/n$ при $n$, равном 2, 3, 4 и 6 (в частности, $n$ не может равняться 5). Всего таких групп, называемых плоскими кристаллографическими (или фёдоровскими), — только 17. Это было доказано выдающимся российским кристаллографом Евграфом Степановичем Фёдоровым.
И создание теории групп как раздела математики, и применение её методов к классификации орнаментов — события XIX века. Интересно, что уже за 500 лет до этого все 17 плоских кристаллографических групп нашли воплощение в работах художников. Как и в случае бордюров, безграничность мира плоских орнаментов порождена разнообразием узоров в образующей «ячейке»: в разных культурах в орнаментах встречаются геометрические фигуры, люди, растения, животные.
Понятие группы — одно из самых часто используемых и полезных в математике. Внешне группы могут быть самыми разными. Целые числа образуют группу относительно операции сложения, в роли единицы — нуль. Все положительные числа — это группа относительно операции умножения, единицей является число 1. Геометрический пример — группа движений (встречалась в данном сюжете и в статье «Геометрическая кристаллография»). В комбинаторике важна группа перестановок какого-либо множества — всевозможные взаимно однозначные отображения этого множества на себя.
Приведём детальное объяснение того, что типов периодических бордюров только 7. Это следует из таблицы умножения для движений в группе бордюра. Создавая таблицу, необходимо учесть, что симметрия относительно горизонтальной прямой только одна, а для описания остальных движений придётся использовать числовой параметр.
Введём прямоугольную систему координат $Oxy$, в которой ось $Ox$ — средняя линия бордюра. Будем использовать следующие обозначения: $H$ — симметрия относительно оси $Ox$; $V_a$ — симметрия относительно вертикальной прямой $x=a$; $R_a$ — центральная симметрия относительно точки $(a;0)$; $T_a$ — параллельный перенос на $a$ вдоль оси $Ox$ (при $a>0$ — вправо); $G_a$ — скользящая симметрия, композиция $H$ и $T_a$.
Результаты композиций, т. е. попарных умножений таких преобразований, можно представить в виде таблицы. Напомним, что при умножении преобразований важен их порядок. В таблице произведений первым выполняется преобразование из выбранного столбца, а затем — из строки.
Воспользуемся приведёнными данными для анализа структуры группы движений бордюра. Напомним, что наличие в группе параллельных переносов необходимо. Формально, из четырёх остальных видов преобразований $H$, $V$, $R$ и $G$ в группе могут отсутствовать все четыре вида, присутствовать только один, только два или только три (в разных сочетаниях), все четыре. Всего получается $2^4=16$ вариантов.
Но из таблицы умножения вытекает, что реализуются не все формально возможные варианты. Например, вариант, представленный в шестом столбце, невозможен, так как вместе с двумя осевыми симметриями в группу должно входить и их произведение — центральная симметрия. В итоге остаются только семь комбинаций преобразований и, соответственно, семь разновидностей бордюров.
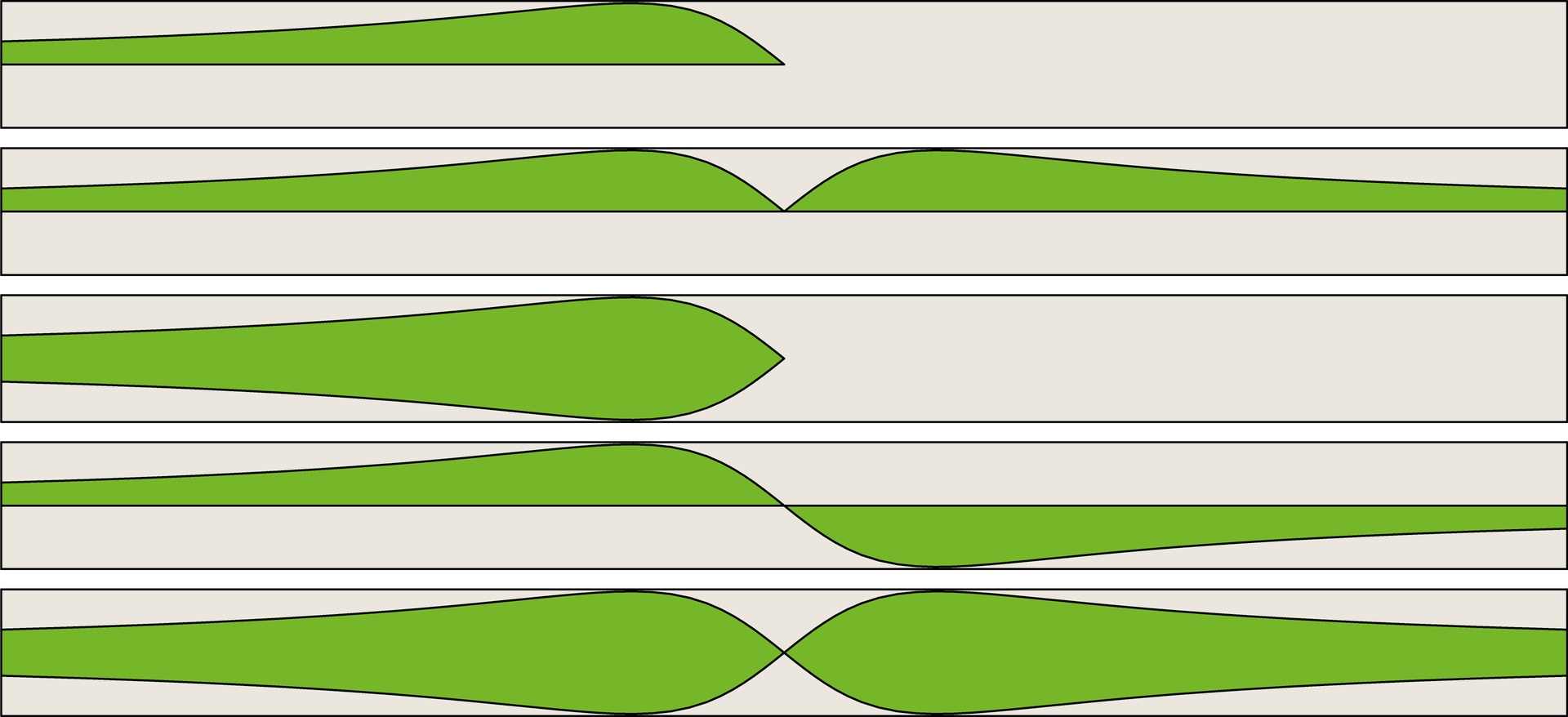
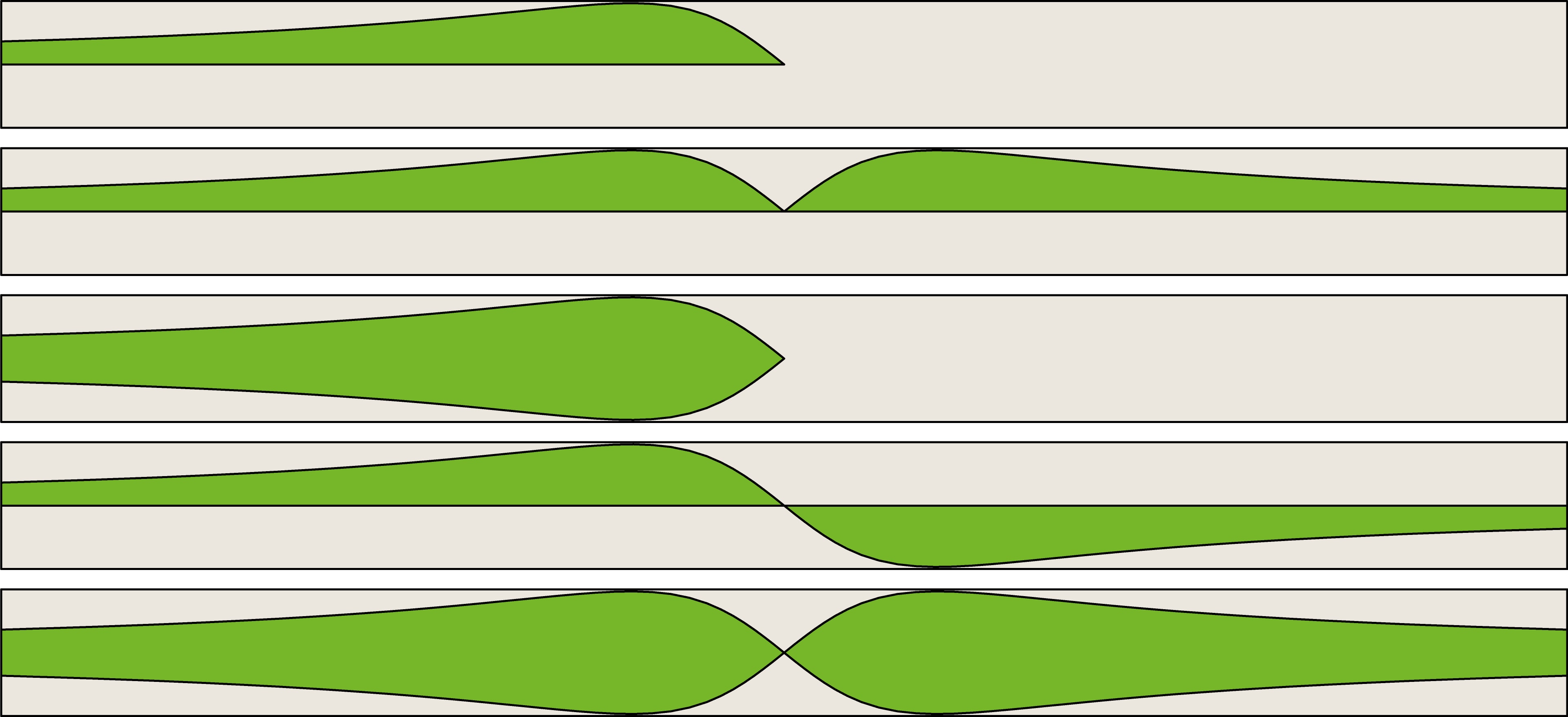
В архитектуре и в отделке мебели встречаются бордюрные узоры, не являющиеся периодическими. В классических бордюрах базовый прямоугольник порождает повторяющуюся картинку. Но можно получить «бесконечно» длинную ленту простым растяжением, неограниченным удлинением прямоугольника, с сохранением имеющихся симметрий. По числу типов прямоугольных узоров появятся ещё пять типов бордюров — с непериодическими узорами. В каждом таком узоре сохраняется группа движений начального прямоугольника: тривиальная, с одной симметрией, с тремя.
Среди этих движений нет переноса — обязательного элемента в группах классических бордюров, поэтому пятёрку непериодических узоров обычно не включают в классификацию бордюров.
Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — [Глава 4 «Двумерная кристаллография»].
Вейль Г. Симметрия. — М.: Наука, 1968. — [Третья лекция «Орнаментальная симметрия», стр. 107—137].
Мальцев А. И. Группы и другие алгебраические системы
Шубников А. В, Копцик В. А. Симметрия в науке и искусстве. — 2‐е изд., перераб. и доп. — М.: Наука, 1972.
Schattschneider D. Enumerating Symmetry Types of Rectangle and Frieze Patterns: How Sherlock Might Have Done It