Развитие компьютеров привело к созданию больших собраний оцифрованных текстов на разных языках — так называемых лингвистических корпусов. Эти корпуса можно обрабатывать методами математической статистики. Математические модели, порой неожиданно простые, но эффективные, позволяют компьютерным лингвистам предложить человечеству и конкретному пользователю решение задач, связанных с автоматической обработкой естественного языка: распознавание речи, определение языка текста и машинный перевод, классификация текстов по темам, извлечение знаний из текста, выделение ключевых слов, анализ тональности текста (т. е. выяснение, содержится ли в нём положительная или отрицательная оценка), обнаружение спама, создание чат-ботов и т. д.
Рассмотрим две задачи — автоматическое определение языка текста и исправление опечаток, хорошие решения которых основаны на анализе частотности отдельных букв и слов, а также их сочетаний в реальных текстах. Удивительно, но такой подход позволяет решать эти задачи, не обладая знаниями ни о грамматических правилах языков, ни о смыслах анализируемых текстов.
Определение языка текста. Предположим, что компьютер получил задание определить, на каком языке написан такой текст:
тя има и естетическа страна.
Эта болгарская фраза означает «При том, что математика — строгая наука, она имеет и эстетическую сторону». Компьютер не владеет языками, но у него есть список языков, к одному из которых надо отнести этот текст. Будем считать, что круг кандидатов не слишком широк: английский, белорусский, болгарский, немецкий, русский, украинский, французский языки.
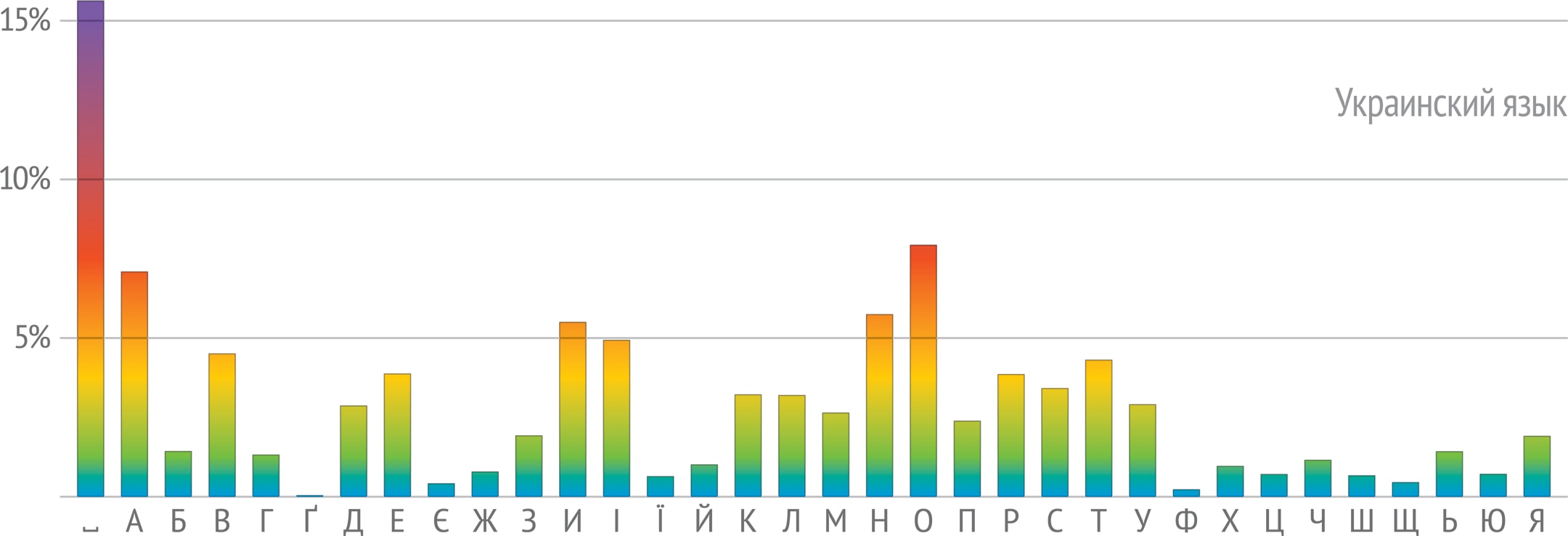
Самая простая идея, которая приходит в голову, — определять язык по алфавиту. В нашем случае это кириллица, поэтому сразу можно отбросить английский, немецкий и французский языки. Но этот метод не решит задачу полностью, например, он плохо справляется с русским и болгарским языками: болгарский алфавит — часть русского (в болгарском нет букв Ё, Ы, Э), так что любой болгарский текст можно принять за русский. Соотношение русского и украинского алфавитов сложнее, ни один не является частью другого: в украинском нет буквы Ъ, зато есть буквы для обозначения гласных звуков Є, І, Ї и согласного Ґ. Но все буквы данной фразы в нём присутствуют. В белорусском нет И (вместо неё используется буква І), поэтому он не подходит. Итак, алфавитный подход с задачей не справляется: осталось три языка-кандидата.
Наличие лингвистических корпусов позволяет анализировать языки, находить характеристики, которые их различают. В частности, «паспортом» языка может служить набор частот, с которыми в среднем встречаются буквы в этом языке.
На частотность букв обратили внимание ещё в докомпьютерную эпоху. Например, в телеграфной азбуке Морзе, возникшей в первой половине XIX века, наиболее часто используемым буквам ставили в соответствие более короткие сочетания точек и тире. Так, самые частые в английском языке буквы E и T кодируются односимвольно — точкой и тире соответственно. Эти буквы можно встретить и в начале верхнего ряда стандартной английской раскладки клавиатуры, унаследованной от пишущих машинок, — QWERTY. А в немецкой раскладке привычный глазу ряд заменён на QWERTZ — буква Y в немецком языке встречается существенно реже, чем Z, и сослана на периферию. Ещё один пример: в криптографии простые шифры на основе замены букв утратили значение после того, как были изучены частотные характеристики языков. Естественно, в XIX веке подсчёты частотности выполнялись вручную. Теперь же, с появлением лингвистических корпусов, частоты букв или слов можно посчитать на компьютере, причём эти данные будут более точными, объективными.
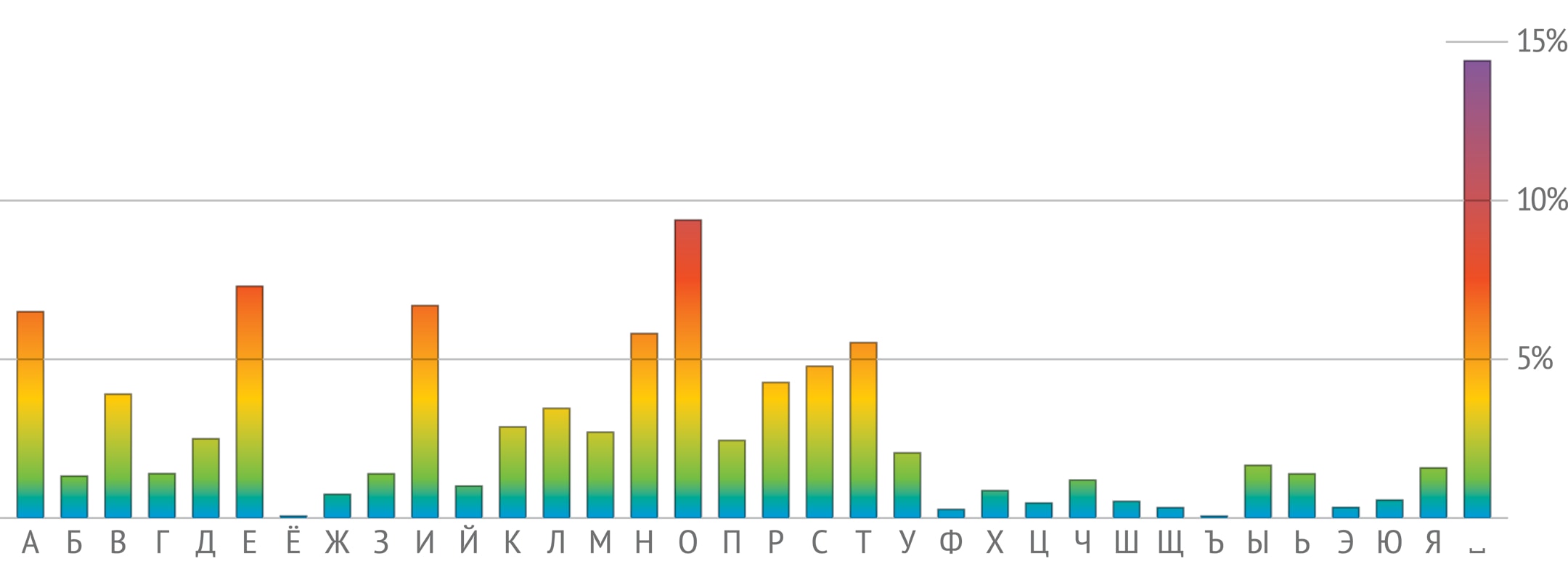
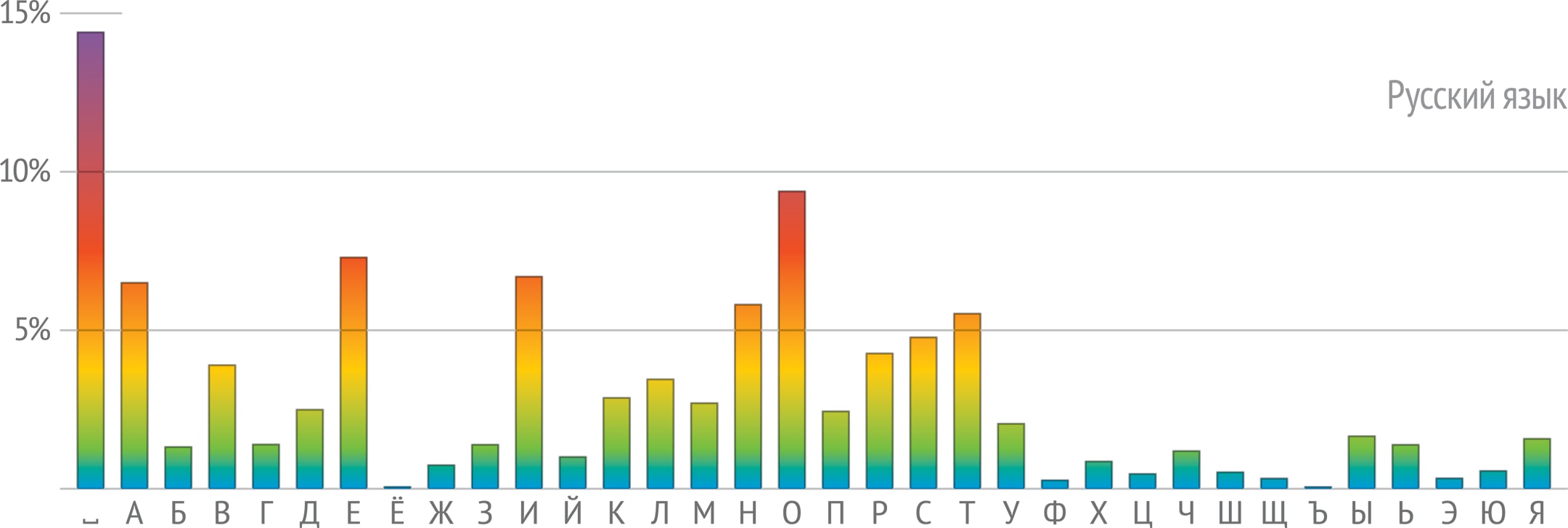
Если условиться, что русский алфавит состоит из 33 букв и пробела, то окажется, что самый частый символ — это пробел (14,46%), дальше следуют гласные О (9,42%), Е (7,33%), И (6,72%), А (6,52%) и согласные Н (5,83%), Т (5,56%). А реже всего встречаются буквы Ф (0,27%), Ъ (0,03%) и Ё (0,01%). Конечно, в каждом конкретном тексте частоты могут отличаться от приведённых, но эти отклонения будут несущественными.
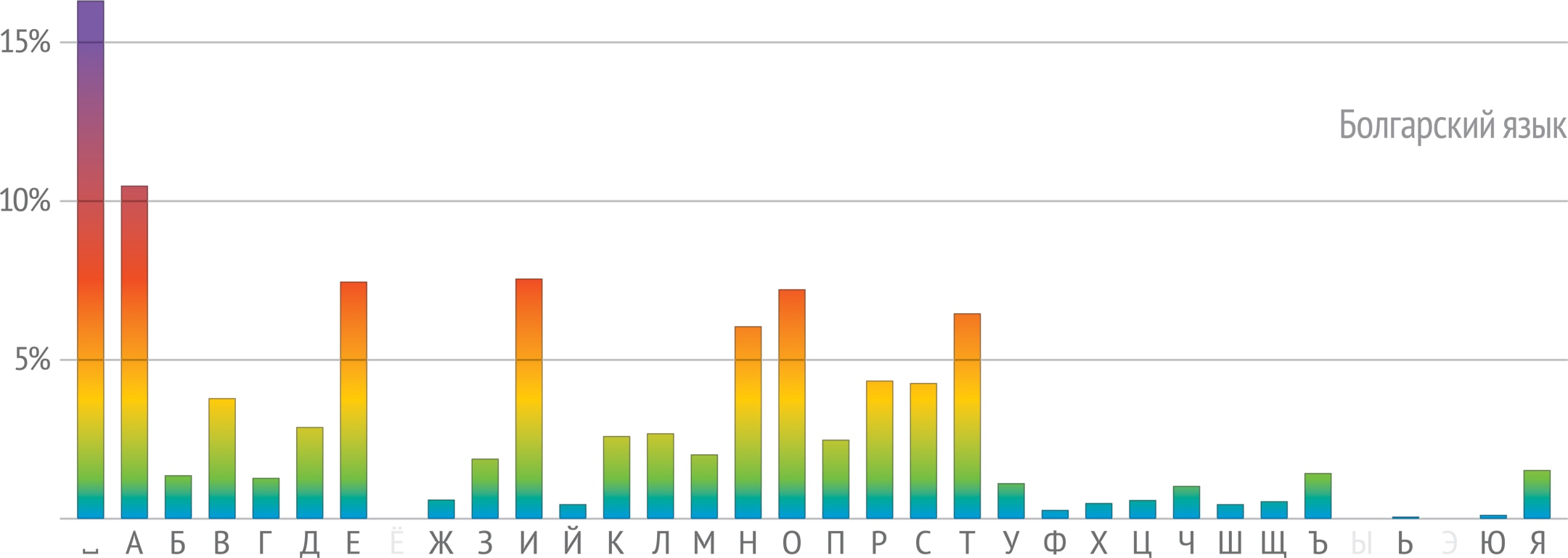
А вот в болгарском языке частоты букв будут другими. Первыми после пробела идут те же четыре гласные, что и в русском, но в обратном порядке: А, И, Е, О. Буква Ъ в русском языке — редкость, а в болгарском употребляется в разы чаще: она обозначает особый гласный звук типа краткого «а» и встречается даже в самом слове български. Последней по частотности буквой является Ь. Всё это показывает, что частотность букв действительно является индивидуальной характеристикой языка.
В компьютерном анализе (например, при определении языка) текст — это последовательность букв. В простейшей модели принимается, что каждая буква в этой последовательности появляется независимо от предыдущих, т. е. текст рассматривается как цепь независимых случайных событий: «прочитав» несколько букв, читатель не знает, что ждёт его дальше. Вследствие независимости вероятность встретить данную последовательность букв в выбранном языке равна произведению вероятностей (частот) появления букв в этом языке.
Зная частотности букв для каждого из трёх языков-претендентов, можно найти вероятность появления всей фразы:
Получается, что вероятность случайного появления этой фразы в болгарском языке в 300 раз больше, чем в русском, и в 300,000 раз больше, чем в украинском. Если о происхождении фразы нет априорной информации, то языки-кандидаты считаются равноправными. Это позволяет сравнивать вероятности появления фразы в разных языках, представив их более привычно, в процентах:
болгарский — 99,65%, русский — 0,3497%, украинский — 0,0003%.
Следовательно, выбрав вариант с максимальной вероятностью, в данном примере получим правильный ответ: фраза написана по-болгарски. Любопытно, что такой простой алгоритм неплохо сработал даже на тексте небольшой длины. Но так бывает не всегда. Например, для названия этой книги Математическая составляющая получается неожиданный результат:
болгарский — 51,55%, русский — 40,75%, украинский — 7,7%.
Симпатия этого алгоритма к болгарскому языку объяснима и носит общий характер: в нём меньше букв, чем в русском или украинском языках, а значит, частотность отдельной буквы будет в среднем чуть больше. Поэтому большинство нестандартных текстов алгоритм сочтёт болгарскими.
Точность определения языка текста можно повысить, если рассматривать не частоты букв по отдельности, а частоты комбинаций символов некоторой длины. Дело в том, что, в отличие от применённой выше простейшей модели, буквы в реальном тексте не независимы: на самом деле каждая буква зависит от предшествующих, по крайней мере — от предыдущей. Так, по правилам русского языка после Ъ могут идти только буквы Е, Ё, Ю или Я. В болгарском после Ъ можно встретить и букву Л, причём это в 10 раз вероятнее, чем встреча с Е, Ю и Я, вместе взятыми. А в украинском И почти не используется после пробела — значит, наша первая фраза со словами има и едва ли может быть украинской.
Эту идею академик Андрей Андреевич Марков (1856—1922) воплотил в математической модели, которая в его честь получила название «цепь Маркова». Он изучил распределение гласных и согласных в последовательности из 20,000 букв в романе «Евгений Онегин» (первая глава и начало второй). Основной вывод гласил: «Мы видим, что вероятность букве быть гласной значительно изменяется, в зависимости от того, предшествует ей гласная или согласная». Подсчёты А. А. Маркова показали, что общая доля гласных — 43,2%, но вероятность встретить гласную после гласной уменьшается до 12,8%, а после согласной — возрастает до 66,3%.
Получается, что в реальном тексте имеем дело не с вероятностями независимых случайных событий, а с условными вероятностями последовательно происходящих событий. В марковской модели будущее зависит от настоящего, а вот прошлое можно не анализировать: его влияние заложено в настоящем. Житейский пример: предсказывая погоду на завтра, можно ориентироваться на сегодняшнюю. Зимняя гроза — редкое явление, так что если сегодня гроза, то завтрашний день может оказаться и солнечным, и дождливым, но вряд ли выпадет снег. С другой стороны, если сегодня идёт снег, то увидеть завтра грозу — маловероятно.
Марковские цепи как математический инструмент можно использовать для анализа распределения не только гласных и согласных в данном языке, но и для всех пар букв алфавита. Зависимость буквы от предшествующей заметить несложно. Например, в русском языке среди пар, начинающихся с буквы З, наиболее вероятны сочетания ЗА (29,67%), ЗН (10,18%), З⎵ (пробел после З; 8,36%), а после буквы А те же символы А, Н, ⎵ дают совсем другие результаты: АА (0,03%), АН (9,56%), А⎵ (20,36%).
Для решения задачи определения языка текста можно сравнивать частотные характеристики пар из одинаковых символов в разных языках. Например, тройки лидеров среди пар, начинающихся с буквы З: в русских текстах — ЗА, ЗН, З⎵; в украинских — ЗА, З⎵, ЗН; в болгарских — ЗА, ЗИ, ЗВ.
Зная частоты всевозможных пар, можно в каждом из языков-кандидатов найти вероятность в марковской модели словосочетания Математическая составляющая, которое рассматривается как последовательность пар: ⎵ М (буква М является началом слова), МА, АТ, ТЕ, ЕМ и т. д. Вероятность всего словосочетания находится как произведение вероятностей этих пар. Результаты (округлённые) дают ответ на вопрос, где могла появиться такая книга:
болгарский — 0,06%, русский — 99,94%, украинский — 0,00003%.
А для фразы, с которой начался разговор (При все че математиката…), степень уверенности у марковской модели почти абсолютная: вероятность, что фраза написана по‐болгарски, равна 99,99991%!
Частотность последовательностей из двух (а лучше даже трёх) букв — очень точная характеристика языка. Приведённый метод — основа всех применяемых определителей языка, самый известный — модуль в Google Translate. Получается, что для решения этой лингвистической задачи не требуется знание языков, работает чистая статистика.
Исправление опечаток. Текстовые редакторы и смартфоны решают эту задачу методами, сходными с использовавшимися в задаче определения языка. Только теперь сравниваются частоты не букв, а слов и их последовательностей в выбранном языке.
Предположим, что пользователь ввёл фразу:
а задача компьютера — найти и исправить в ней опечатки. Человеку сразу понятно, что опечатка допущена в слове руква, а должно быть написано слово рука. Попробуем научить этому и компьютер, используя гигантский лингвистический корпус русскоязычных текстов общей длиной 16 миллиардов слов.
На первом этапе отыщем подозрительные слова: такие слова, которые либо отсутствуют в корпусе, либо встречаются там очень редко, скажем, для определённости — не более 100 раз (причиной возникновения в корпусе таких слов могут быть опечатки). А слова, которые встречаются более 100 раз, составляют словарь.
Вот сведения о частотах наших четырёх слов в корпусе: его — 46,643,493, руква — 50, немного — 3,475,296, болит — 203,993. По принятой договорённости алгоритм решает, что в слове руква допущена опечатка.
На втором этапе определим набор слов, одно из которых, возможно, хотел ввести пользователь. Очевидно, что эти слова должны быть похожими, близкими в каком-то смысле к слову руква: вряд ли человек хотел напечатать локоть, а получилась руква.
Для измерения близости слов в лингвистике обычно используется расстояние Дамерау —Левенштейна (названное в честь американского лингвиста и российского математика). Это расстояние равно минимальному числу «шагов», необходимых для превращения одного слова в другое. Такими шагами являются типовые, стандартные ошибки при наборе текста: замена одной буквы на другую, добавление или удаление буквы, перестановка соседних букв.
Например, расстояние между словами собака и кошка равно 3: замена с на к (получится кобака); замена б на ш (кошака); удаление первой а (кошка). Есть и другой путь длины 3: собака → соака → сошка → кошка. Но осуществить превращение меньше чем за 3 шага не удастся.
Такое расстояние между словами обладает всеми привычными свойствами расстояния между точками на плоскости: неотрицательность, симметричность (расстояние от собака до кошка равно расстоянию от кошка до собака), справедливо неравенство треугольника (см. «Далёкое близкое»). Теперь можно формализовать ощущение, что слово руква легко получается из слова рука, но не из слова локоть: расстояние Дамерау —Левенштейна от рука до руква равно 1, а от локоть до руква — 5.
Опечаток в одном слове обычно немного, чаще всего одна. Найдём в словаре все слова, которые отстоят от подозрительного слова руква на расстояние 1. Слов-кандидатов не так много: рука (удаление в), рукав (перестановка а и в), буква (замена р на б) и рукава (добавление а). На этом можно остановиться и предложить пользователю список кандидатов — пусть выбирает сам. Именно так работает, например, проверка орфографии в Microsoft Word.
Но компьютер может пойти дальше и попробовать исправить опечатку, т. е. выбрать самого вероятного кандидата и предложить его пользователю (так поступает Google Docs), а может и сам подставить его в предложение (так обычно работают модули в смартфонах, «помогающие» набирать текст). Этот выбор единственного кандидата — следующий этап алгоритма, который можно реализовывать по-разному.
Простейшее, но неплохо работающее решение — выбрать самое частотное слово. Частоты слов-кандидатов в корпусе таковы: рука — 350,883, рукава — 126,817, буква — 107,262, рукав — 66,094. Как видно, в примере Его руква немного болит такой автоматический выбор совпадает с человеческим.
А вот во фразах
Здесь написана неправильная руква и У меня руква порвался
простейшее решение — заменить руква на рука — будет ошибочным. Чтобы алгоритм работал более «разумно», надо каким-то образом учитывать слова в контексте фразы. И здесь на помощь снова приходят марковские цепи.
Воспользуемся идеей, которая применялась в анализе по буквам, и попробуем предсказать следующее слово по последнему из виденных. Например, слово неправильная встречается в корпусе 50,267 раз; пары неправильная рукава и неправильная рукав в корпусе отсутствуют, неправильная рука встречается 4 раза, неправильная буква — 53 раза. На примере фразы Здесь написана неправильная руква видно, что метод выбора самой частотной пары соседних слов более эффективный, чем простейший алгоритм.
Дальнейшее улучшение алгоритма состоит в том, что учитываются и слово, идущее перед подозрительным словом, и слово, идущее после него. Определяются частоты обеих пар, найденные вероятности перемножаются. На примере фразы У меня руква порвался даже без статистических данных видно, что после сравнения произведений вероятностей пар выбор наибольшего выглядит достоверным решением:
(меня рука) $\cdot$ (рука порвался); (меня рукава) $\cdot$ (рукава порвался);
(меня буква) $\cdot$ (буква порвался); (меня рукав) $\cdot$ (рукав порвался).
Получается хорошо работающее исправление опечаток.
Разумеется, и этот алгоритм можно и нужно совершенствовать. Во‐первых, вероятности одношаговых опечаток отличаются: например, перестановка соседних букв в слове значительно вероятнее, чем замена буквы на удалённую от неё на клавиатуре (скажем, заменить б на р не так-то просто). Во‐вторых, можно встретиться с правильным, имеющим смысл словосочетанием, которое отсутствует в корпусе, и тогда произведение вероятностей будет равно нулю (пример: словосочетание} работающее исправление, которое мы использовали в конце предыдущего абзаца, в корпусе пока отсутствует). В‐третьих, рассмотренный вариант марковской цепи связывает слово только с ближайшими соседями, хотя в языке встречаются зависимости и на далёких расстояниях. Например, во фразе Руква у рубашки, которую Вася купил в аэропорту, оказались слишком короткими, выбирая на замену рукав или рукава, придётся опираться не на соседние, а на далёкие слова оказались и короткими. В‐четвёртых, сделав опечатки, можно получить фразу со словами из словаря, но ошибочную: например, У меня лукав порвался. Алгоритм такую фразу ни в чём не заподозрит. Впрочем, усложнение алгоритма позволяет справиться с подобными затруднениями.
Компьютерная лингвистика. Лингвистические корпуса — фундамент компьютерной лингвистики, неисчерпаемый источник сведений о языке. Их анализируют и профессионалы — лингвисты и компьютерные специалисты, и начинающие исследователи. Даже школьник может самостоятельно написать программу для поиска и проверки закономерностей в языковых массивах.
Самый известный ресурс для русского языка — это Национальный корпус русского языка (НКРЯ), в основной части которого содержится 283 миллиона слов, а всего — около 600 миллионов слов. Корпус Araneum Russicum Maximum, объёмом 16 миллиардов слов, мы использовали для определения частоты слов при исправлении опечаток. Он состоит из текстов, собранных из интернета, а это очень важный способ создания современных лингвистических ресурсов: ведь в сети лежит множество доступных текстов. К сожалению, эти корпуса нельзя сохранить на своём компьютере, и возможности пользователя ограничены веб-интерфейсом. На помощь приходят другие источники: так, определение языка проводилось на основе свободно распространяемых корпусов из проекта Universal Dependencies, где в едином формате представлены данные 70 языков.
Понятно, что частота отдельных слов и их сочетаний существенно зависит от набора текстов, включённых в корпус. У корпуса художественных текстов и корпуса текстов новостных — разный «словарный запас». Универсального, правильного корпуса для языка не существует, но надо научиться даже из отдельных, так или иначе «окрашенных» корпусов извлекать общие свойства, черты, особенности данного языка. Это желание вызывает в памяти восклицание основателя палеонтологии Жоржа Кювье: «Дайте мне одну кость, и я восстановлю животное!». По сути — это те задачи, из которых и родилась математическая статистика: как получить представление о ненаблюдаемом целом по некоторой выборке. И для их решения были созданы методы, более продвинутые, чем простой подсчёт частот.
Один из приёмов — усреднение, согласование значений частот по разным фрагментам корпуса, чтобы уменьшить влияние отдельных текстов. Например, частотность слова якорь в текстах НКРЯ, распределённых по десятилетиям, с 1970 года до наших дней, выглядит странно: 1970‐е — встречается 160 раз на миллион; 1980‐е — 6,8; 1990‐е — 8,4; 2000‐е — 6,6; 2010‐е — 6,7. Причина аномалии — включённая в НКРЯ «Книга о якорях», изданная в 1973 году. В ней одной слово якорь встречается 1769 раз, а во всём корпусе — только 2896. Полученная простым подсчётом частотность слова якорь по всему массиву — 21,9 на миллион — явно завышенная. Но если упорядочить значения частот по десятилетиям и взять число из середины списка (медиану), то получится более реальный результат: 6,8 на миллион. Можно учитывать и дисперсию, т. е. оценивать разбросанность значений: как часто и на сколько они отклоняются от среднего значения. Такой метод применял ещё А. А. Марков, работая с текстом «Евгения Онегина»: он проверял устойчивость, независимость своих результатов от способов подсчёта. Более сложные методы используются для предсказания «настоящих», истинных частот сочетаний слов: надо уметь отличать те, что в корпусе не встретились, но в принципе вполне возможны, от тех, что не встретились, потому что практически невозможны.
В заключение отметим, что автоматическая обработка языка начала активно развиваться в 1950‐е годы. В частности, первое время машинный перевод основывался на созданных вручную правилах, предписывавших, как именно переводить то или иное словосочетание при определённых условиях. Постепенно выяснилось, что сочинение правил требует огромных затрат человеческого труда, а работают они всё равно плохо.
Поэтому в конце 1980‐х годов на первый план в автоматической обработке естественного языка вышел статистический подход: посмотрим, как похожие задачи решались до нас человеком, и найдём решение, комбинируя его из готовых частей. Это стало возможным после появления лингвистических корпусов. Методы, рассмотренные нами на примерах, прежде всего частотность букв, слов и сочетаний, стали основой решения задач компьютерной лингвистики, перечисленных в начале статьи. Интересно, но временами создаётся впечатление, что алгоритмы и программы, основанные на статистическом подходе, в какой‐то мере освоили язык.
Например, эффективность применения марковских цепей неявно связана с грамматикой и структурой языка. В примере со словосочетанием Математическая составляющая при выборе одного из трёх языков помогла, в частности, высокая частотность сочетания ая в русском языке. Дело в том, что в русском языке в женском роде встречается окончание ‐ая, причём часто, а в болгарском и украинском в такой форме было бы просто ‐а.
В XXI веке математика предложила новые подходы к автоматической обработке языка. Бурное развитие искусственных нейронных сетей, обучаемых на огромных массивах входных данных, дало возможность решать самые разные задачи компьютерной лингвистики. А принципы работы нейронных сетей ещё больше приближают компьютер к тому, что можно назвать пониманием естественных языков. На данном этапе компьютерная лингвистика всё больше превращается в одну из разновидностей машинного обучения. Но если мы хотим разобраться с тем, что же происходит при обработке текстов искусственными нейронными сетями, нужен именно лингвистический взгляд. Лингвистика как наука необходима и для более полного использования возможностей уже существующих инструментов, и для построения новых математических моделей.
Частотность важна в реальной деятельности, например, в прикладной лингвистике и криптологии (в ней две ветви: криптография и криптоанализ), встречается и в беллетристике.
Рассказ Эдгара По «Золотой жук» (1843) — одно из первых популярных (и художественных!) изложений как реального способа шифрования методом подстановки, замены букв какими-то знаками, так и метода его расшифровки — частотного анализа. А в 1903 году Артур Конан Дойл в серии историй о Шерлоке Холмсе опубликовал рассказ «Пляшущие человечки», математически весьма схожий с «Золотым жуком».
Ляшевская О. Н., Шаров С. А. Частотный словарь современного русского языка (на материалах Национального корпуса русского языка). — М.: Азбуковник, 2009. — [http://dict.ruslang.ru/freq.php].
Прикладная и компьютерная лингвистика / Под ред. И. С. Николаева, О. В. Митрениной, Т. М. Ландо. — М.: Ленанд, 2016.
Марков А. А. Пример статистического исследования над текстом «Евгения Онегина», иллюстрирующий связь испытаний в цепь
Марков А. А. Об одном применении статистического метода