И фотографии, и картины обычно не вызывают сомнений в реальности изображённых на них объектов. Но встречаются и озадачивающие примеры. Самые известные — гравюры Маурица Эшера.
На литографии «Спускаясь и поднимаясь» (1960) изображены идущие по замкнутой лестнице навстречу друг другу две группы. Причём у идущих в одном направлении по ступеням лестницы — бесконечный подъём вверх, а у идущих навстречу — бесконечный спуск. Эшер писал про бесконечную лестницу: «Это нечто замкнутое, кольцевое, словно змея, заглатывающая собственный хвост. Тем не менее, можно нарисовать её в правильной перспективе: каждая ступень выше (или ниже), чем следующая».
На гравюре «Водопад» (1961) представлена «действующая» модель вечного двигателя: поток воды низвергается вниз, по дороге крутит колесо, а потом бежит вниз к… верховьям водопада.
Идея, на которой основаны эти работы, восходит к шведскому художнику Оскару Рутерсварду. В 1934 году, ещё учась в гимназии, он на уроке по латинской грамматике нарисовал первую невозможную фигуру. Работы Эшера — художественное воплощение геометрических моделей, предложенных в 1950‐х годах Лайонелом и Роджером Пенроузами (отец и сын, психолог и математик).
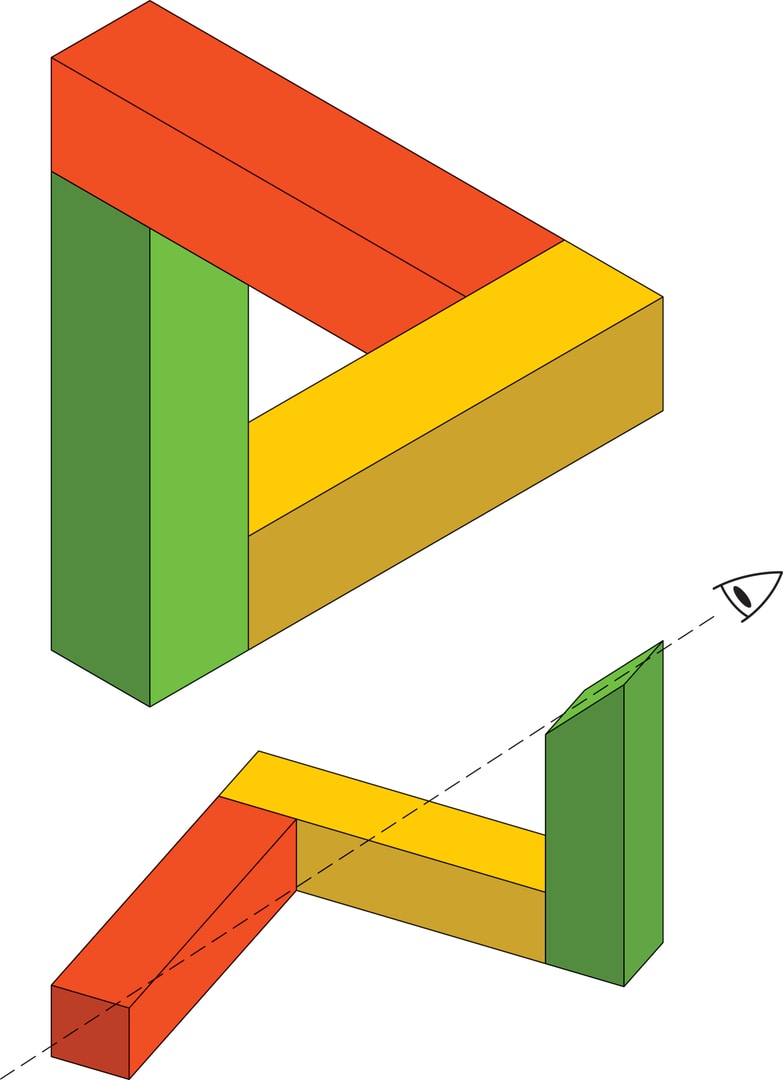
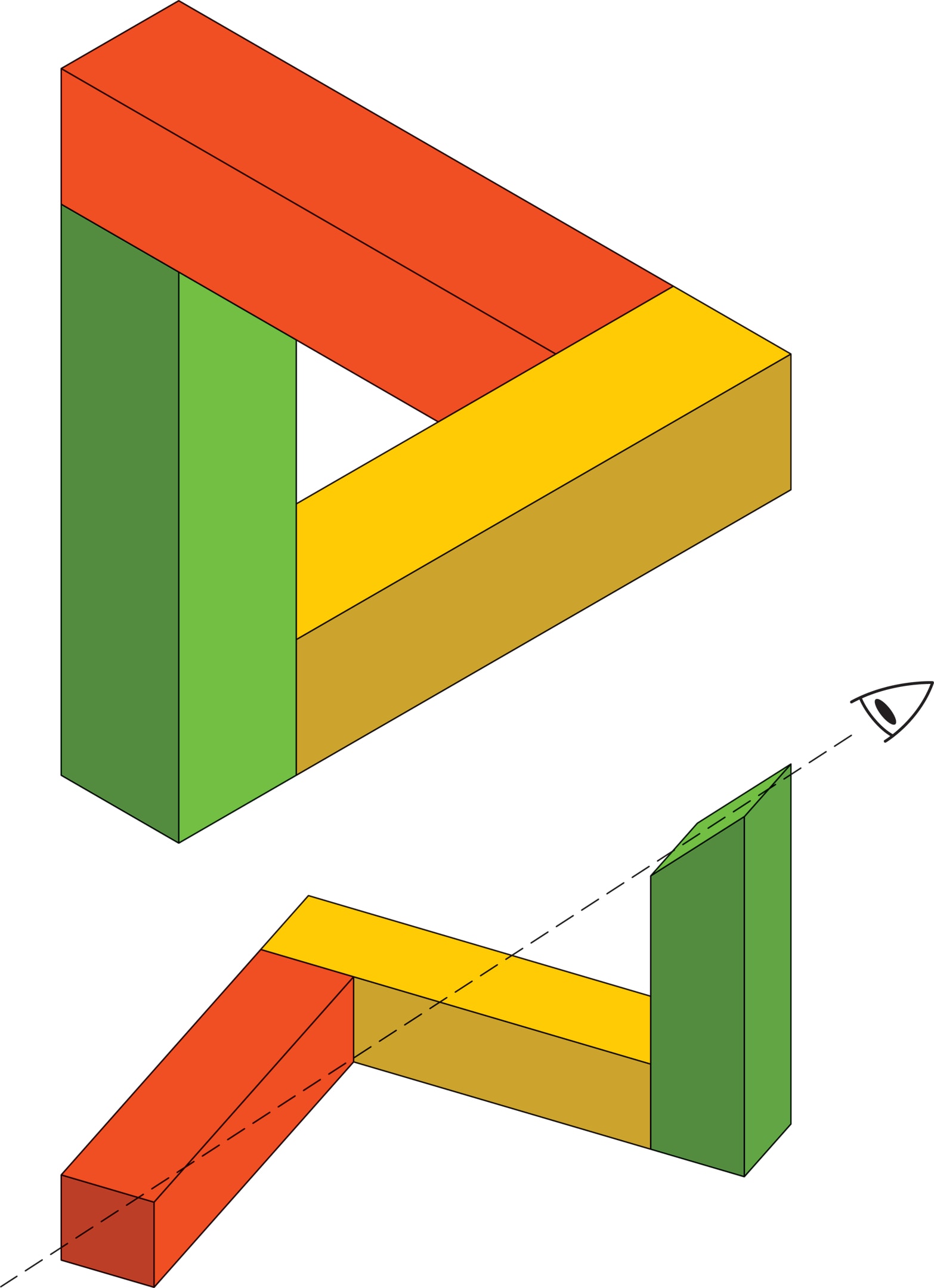
Самая простая из этих моделей, невозможный треугольник, состоит из трёх взаимно перпендикулярных прямоугольных брусков — непрерывной цепочки трёх попарно перпендикулярных рёбер куба. Если смотреть на конструкцию из точки на продолжении диагонали куба, проходящей через крайние концы цепочки, то цепочка замкнётся, превратившись в «треугольник» (в эксперименте стоит закрыть один глаз). На плоском изображении увиденного соединение элементов вызывает ощущение, что такого не может быть.
А на самом деле каждая из подобных «невозможных» фигур обладает реальным прототипом, при взгляде на который лишь с определённых точек видишь то, что существовать, казалось бы, не может! Более того, даже «простой» невозможный треугольник можно получить как портрет цепочек из трёх брусков, края которых устроены по-разному, а в процессе визуального «замыкания» это различие исчезает.