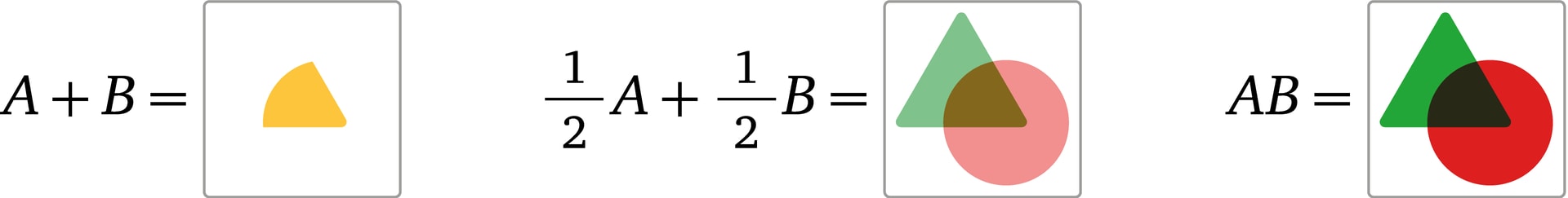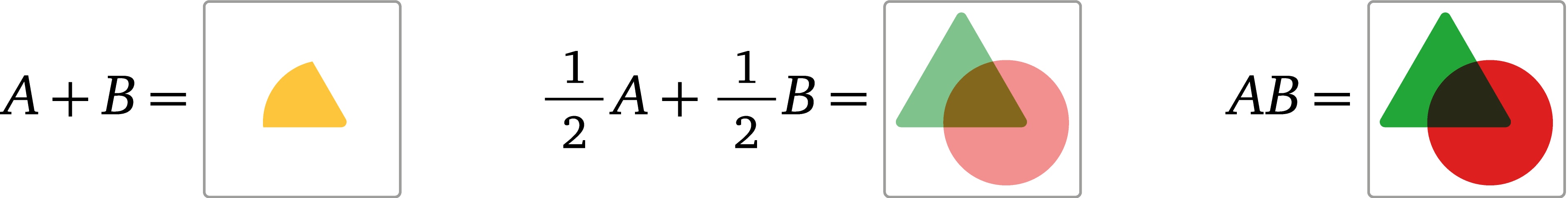Изображения, представленные в компьютере, можно складывать и вычитать, умножать и даже возводить в степень! Именно на арифметических операциях основана работа компьютерных программ с растровыми изображениями, таких как Photoshop или инструментов для обработки фотографий в социальных сетях.
Растровое изображение можно представлять как светящуюся картинку на экране — это прямоугольная таблица, состоящая из ячеек (пикселей). В каждой из них хранится числовой набор $(r;g;b)$, характеризующий яркость трёх базисных цветов (красный, зелёный, синий), из которых складывается цвет пикселя. Целые числа $r$, $g$ и $b$ хранятся в виде байтов: каждая двоичная запись состоит из восьми нулей и единиц, поэтому диапазон значений — от 0 до 255 ($=2^8-1$). Значение 0 означает отсутствие данного цвета в комбинации, значение 255 — яркость цвета максимальна. Примеры: $(0; 0; 0)$ — чёрный пиксел, (255; 255; 255) — белый, (255; 0; 0) — красный, $(0; 100; 0)$ — тёмно-зелёный, $(200; 200; 0)$ — жёлтый.
Арифметические операции над изображениями выполняются попиксельно и покомпонентно. Для одинаково расположенных пикселей $(r_1; g_1; b_1)$ и $(r_2; g_2; b_2)$ их сумма равна $(r_1+r_2; g_1+g_2; b_1+b_2)$, а произведение равно $\left({\left[\frac{r_1r_2}{255}\right]}; {\left[\frac{g_1g_2}{255}\right]}; {\left[\frac{b_1b_2}{255}\right]}\right)$. В сложении сумма} принимается равной 255, если она больше этого числа; в определении произведения квадратные скобки обозначают целую часть числа. В общем, при сложении получается более яркая точка, при умножении — менее яркая. Например, прибавление к картинке белого фона обесцвечивает всю картинку, превращая её в «белое безмолвие». А если умножить цветную картинку на «чёрный квадрат», то образуется квадратная «чёрная дыра».
Непосредственные результаты применения введённых операций обескураживают. Взяв зелёный треугольник ($А$) и красный круг ($B$), в сумме $A+B$ получим жёлтый ломтик в пересечении. Если взять «по половине изображений» $0{,}5A+ 0{,}5B$, уменьшив вдвое яркости всех составляющих, то треугольник и круг по форме сохранятся, но изменятся по цвету: в пересечении фигур будет тёмное пятно, а дополняющие части станут светлее. В произведении $AB$ пересечение фигур будет тёмным, а остальные части сохранят оригинальные цвета.
Но большой класс практических задач можно решить «арифметически», если использовать монохромные, серые маски — изображения с оттенками от чёрного до белого. Рассмотрим чёрно-белые маски $M_A$ и $M_B$, построенные по $A$ и $B$: сами фигуры становятся белыми, а белый фон — чёрным. Ещё две маски, $\overline{M_A}$ и $\overline{M_B}$ — их «антиподы», чёрный и белый меняются местами (вычитание из белого, инвертирование).
Умножение изображения $A$ на его маску $M_A$ даёт изображение треугольника на чёрном фоне, а умножение $B$ на маску $\overline{M_A}$ вырезает чёрный треугольник из изображения с кругом. Наконец, сумма полученных изображений $AM_A+B\overline{M_A}$ — это наложение зелёного треугольника $A$ на красный круг $B$. Аналогично, $BM_B+A\overline{M_B}$ — наложение красного круга на зелёный треугольник.
Приведённые маски были чёрно-белыми, но «подлинно» серые маски тоже применяются. Например, с их помощью можно сделать наложенное изображение полупрозрачным. Две серые маски, линейные комбинации чёрно-белых, порождают полупрозрачное наложение треугольника на круг: $A(0{,}7M_A+0{,}3\overline{M_B})+B(0{,}7\overline{M_A}+0{,}3M_B)$.
Полезные инструменты получаются и при работе только с одним изображением, например, возведение в степень — способ увеличить резкость чёрно-белой фотографии.
Базовые операции рассматривались в простейшей модели, с обработкой по отдельным пикселям. Но используются и инструменты, которые меняют цвет пикселя с учётом цветов окружающих пикселей. Например, усреднение цветов даёт эффект размытия фотографии.