Как уговорить ребёнка выпить злую микстуру? Можно пойти на «математическую» хитрость, и если она сработает, то в дополнение к порции лекарства ребёнок получит поучительное объяснение.
Нальём микстуру в конический бокал и предложим «больному» выпить половину («среднее дипломатическое» для уговаривающего и сопротивляющегося). Большинство автоматически решит, что «половина» — это «половина по высоте», и… выпьет $7/8$ содержимого бокала, т. е. почти всё!
А половина бокала будет выпита, если уровень жидкости понизится примерно на $1/5$ высоты (точнее, на $ 1 - \frac{1}{\sqrt[3]{2})}$). Число $\sqrt[3]{2}$ уже встречалось на предыдущей странице, его появление здесь вызвано похожими соображениями, только формулу объёма шара заменит формула объёма конуса.
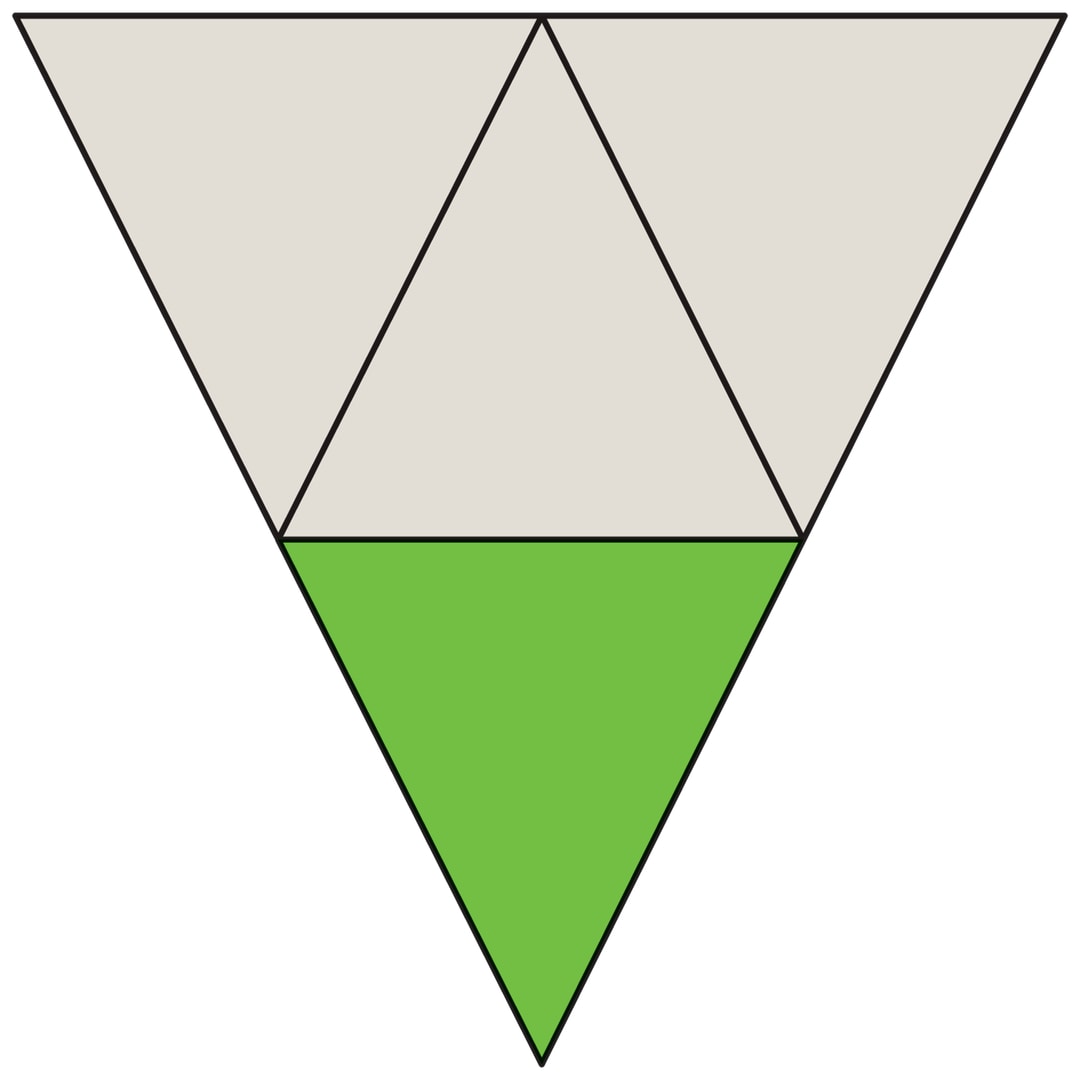
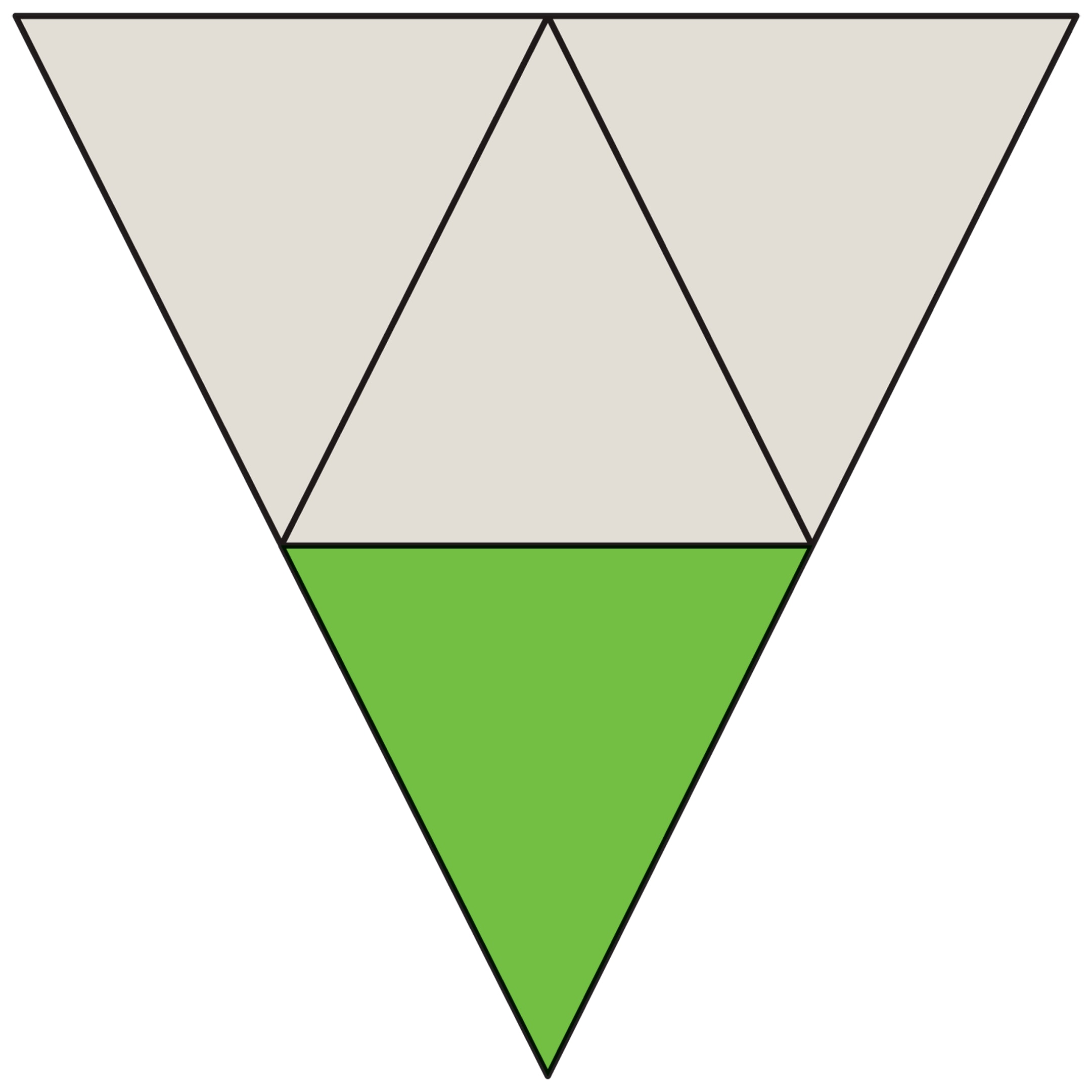
Перечисленные «подходы» к бокалу изображены на рисунках.
Несколько практических замечаний.
Приведённые соотношения действуют для любого конического фужера, так как не зависят от угла конуса.
В математике формулы, связи условий и утверждений в теоремах — часто вещи обратимые, их можно читать-применять и в одну сторону, и в другую. Так и в нашем примере: приведённые математические соображения позволяют разумно обосновать желание выпить больше, чем разрешают.
Сюжеты «Объём шкурки апельсина» и «Конический фужер» удивляют и показывают, как легко впасть в заблуждение в геометрических оценках. Корень подобных ошибок в том, что наш разум, оценивая величины предметов, в первую очередь воспринимает и фиксирует их линейные размеры, а не объёмы.
Поясним примером на плоскости (двумерное пространство). Если в треугольнике провести все три средние линии, то он разделится на четыре одинаковых треугольника. Маленькие треугольники подобны исходному, все стороны уменьшаются в 2 раза; а отношение площадей равно $\frac{1}{4}$, квадрату коэффициента подобия.
В трёхмерном пространстве всё аналогично: например, отношение объёмов шара радиуса $R$ и шара радиуса $2R$ равно $\Big(\frac{1}{2}\Big)^3=\frac{1}{8}$.
В примере с фужером на среднем рисунке заполненная жидкостью часть бокала конус, подобный «большому» конусу фужера, но все его линейные размеры (высота, длина окружности основания и т. п.) вдвое меньше. Поэтому отношение объёмов равно кубу коэффициента подобия — $\Big(\frac{1}{2}\Big)^3$, т. е. $\frac{1}{8}$.