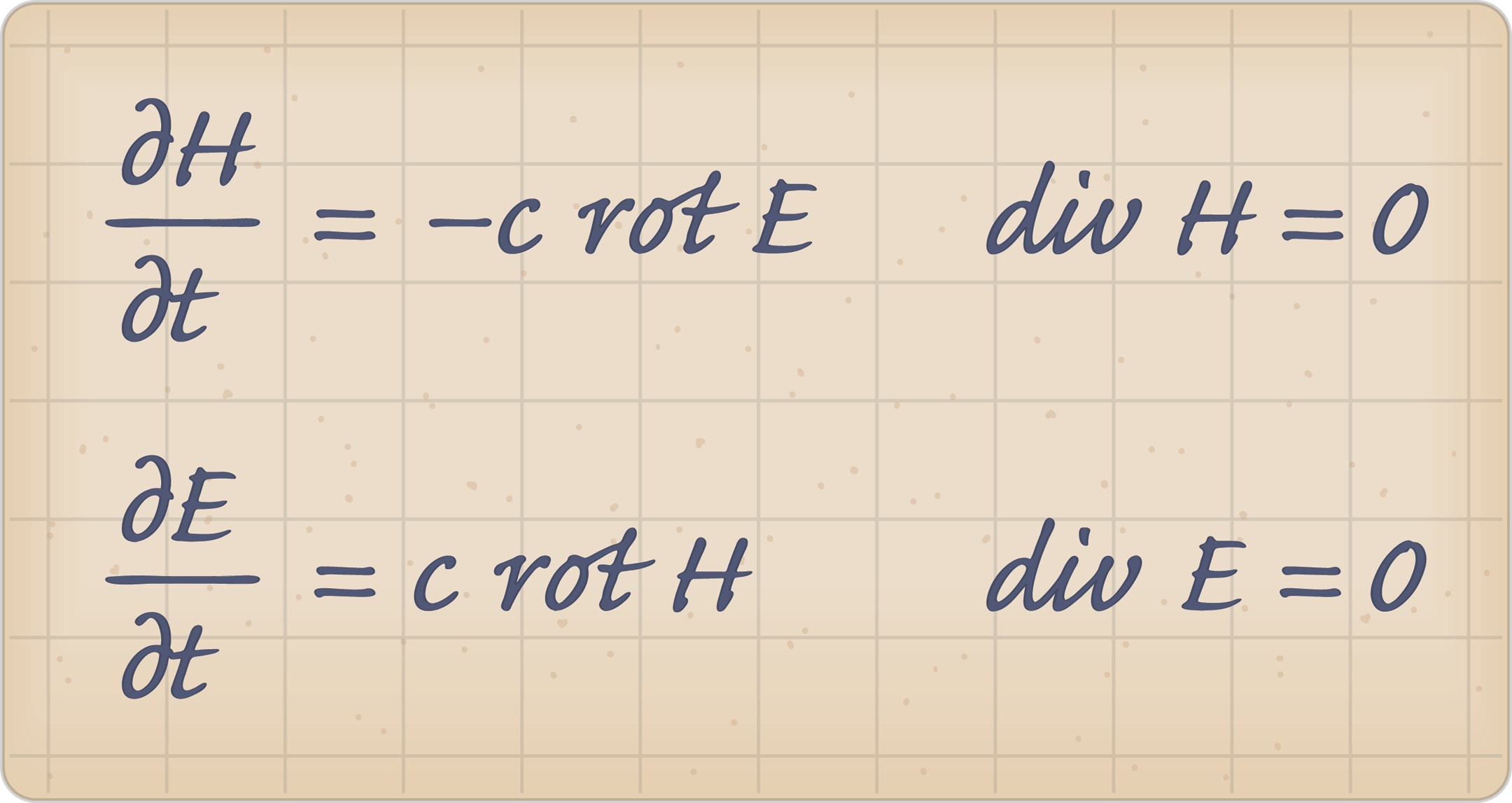Какое научное открытие XX века следует считать наивысшим достижением? Наверное, создание квантовой механики. При этом мы помним и о релятивистской механике (как специальной, так и общей), и о двойной спирали в генетике. Особая роль квантовой механики состоит не только в объяснении происходящего в микромире (на уровне атомов и частиц), но и в порождённых ею новых технологиях. Достаточно упомянуть транзисторы и лазеры, сверхпроводимость и атомную промышленность. Кстати сказать, в квантовую механику существенный вклад внесли математики, разработав для описания квантовых закономерностей адекватный математический аппарат. Более того, даже первое квантовое уравнение для атома водорода решил математик Вейль по просьбе Шрёдингера.
Аналогичный вопрос можно задать и про XIX век. Ответ очевиден: создание электромагнитной теории, ключевым элементом которой являются уравнения Максвелла. Конечно, и здесь мы не забываем другие выдающиеся достижения, такие, как создание термодинамики и статистической механики. Но уравнения Максвелла дали возможность «управлять» электричеством, на смену эпохе пара пришла эра электрической энергии.
В электродинамике у Максвелла были выдающиеся предшественники: Эрстед, Ампер и, конечно, Фарадей. Они экспериментально установили основные законы электродинамики. Были открыты индукционные токи, силовые магнитные линии, явление самоиндукции и т. д. Но, наверное, одно из самых ярких достижений в этой области — это введение в обиход понятия поля. Речь идёт о том, что электричество и магнетизм, так сказать, «пронизывают» всё пространство. Они присутствуют даже тогда, когда в этом месте пространства нет «пробных» зарядов и токов, по действию на которые мы могли бы судить о наличии электрического и магнитного полей. Итак, по Максвеллу, у нас есть два векторных поля: электрическое и магнитное. Они зависят от точки пространства и ещё от времени. Учитывая результаты экспериментов, Максвелл вывел систему уравнений, которым эти поля подчиняются.
Путь к простым по виду уравнениям был мучительно долгим, поскольку длительное время искали подходящие механические аналогии. Главная идея, которой руководствовались Томсон (лорд Кельвин) и Максвелл, — аналогия с вихревым течением идеальной несжимаемой жидкости. Эта жидкость мыслилась как некоторое безмассовое вещество — тончайший эфир, которое заполняет всё пространство и находится в беспрерывном движении. Идея восходит к знаменитому математику Декарту, который пытался построить на подобной основе вихревую теорию материи. Механические аналогии выполнили эвристическое предназначение, и в современных учебниках по электромагнетизму нет даже следов их использования. Но в самих уравнениях отголоски о вихрях и несжимаемости остались — в виде ротора и дивергенции.
Отметим два важных следствия уравнений Максвелла, сыгравших фундаментальную роль в развитии телекоммуникационных технологий и в становлении современных физических представлений о пространстве-времени.
Уравнения Максвелла имеют простые частные решения в случае, когда в каждой точке пространства электрическое и магнитное поля перпендикулярны друг другу и одновременно совершают гармонические колебания с одинаковой частотой, не меняя своего направления. В результате образуется волна, которая распространяется прямолинейно со скоростью света. Тем самым проясняется электромагнитная природа света. В 1888 году Герц нашёл способ генерации электромагнитных волн. Сразу же после этого Попов и Маркони использовали идеи Герца для осуществления практической радиосвязи на расстоянии. Теперь невозможно представить современную цивилизацию без средств связи, основанных на уравнениях Максвелла.
Другое важное последствие уравнений Максвелла — это релятивистская механика. Она создана, в основном, усилиями физиков Лоренца и Эйнштейна, а также математиков Пуанкаре и Минковского. Оказалось, что уравнения Максвелла сохраняют свой вид относительно десятипараметрической группы линейных преобразований четырёхмерного пространства-времени, которую Пуанкаре назвал группой Лоренца. С другой стороны, уравнение второго закона Ньютона в трёхмерном пространстве допускает группу преобразований Галилея, также зависящую от 10 параметров. Основная идея релятивистской динамики состоит в том, что для согласования механики с электродинамикой группу Галилея следует заменить группой Лоренца. Идеи релятивистской механики сформировали наши современные представления о пространстве и времени.
Уравнения Максвелла не только стали математическим фундаментом электродинамики, но и позволили сохранить целостность всей физической картины мира.