‍Формат книги

В выход­ных дан­ных этой книги ука­зано:

А что это зна­чит? И как опре­де­лить размер стра­ницы книги по этим зага­доч­ным чис­лам?

С помощью линейки или гла­зо­мера быстро убеж­да­емся, что и 70, и 100 — это не размеры стра­ницы ни в сан­тимет­рах, ни в мил­лимет­рах…

Во‐пер­вых, всю надпись надо воспри­нимать как еди­ное целое.

Во‐в­то­рых, в этих чис­лах есть мет­ри­че­ский смысл, только речь идёт не о разме­рах стра­ницы книги, а о разме­рах стан­дарт­ного типограф­ского листа 70 на 100 см, а $1/16$ — доля стра­ницы книги на таком листе. Теперь ста­но­вится понят­ным то, как про­из­но­сят про­фес­си­о­налы назва­ние нашего формата: «70 на 100 в одну шест­на­дца­тую долю».

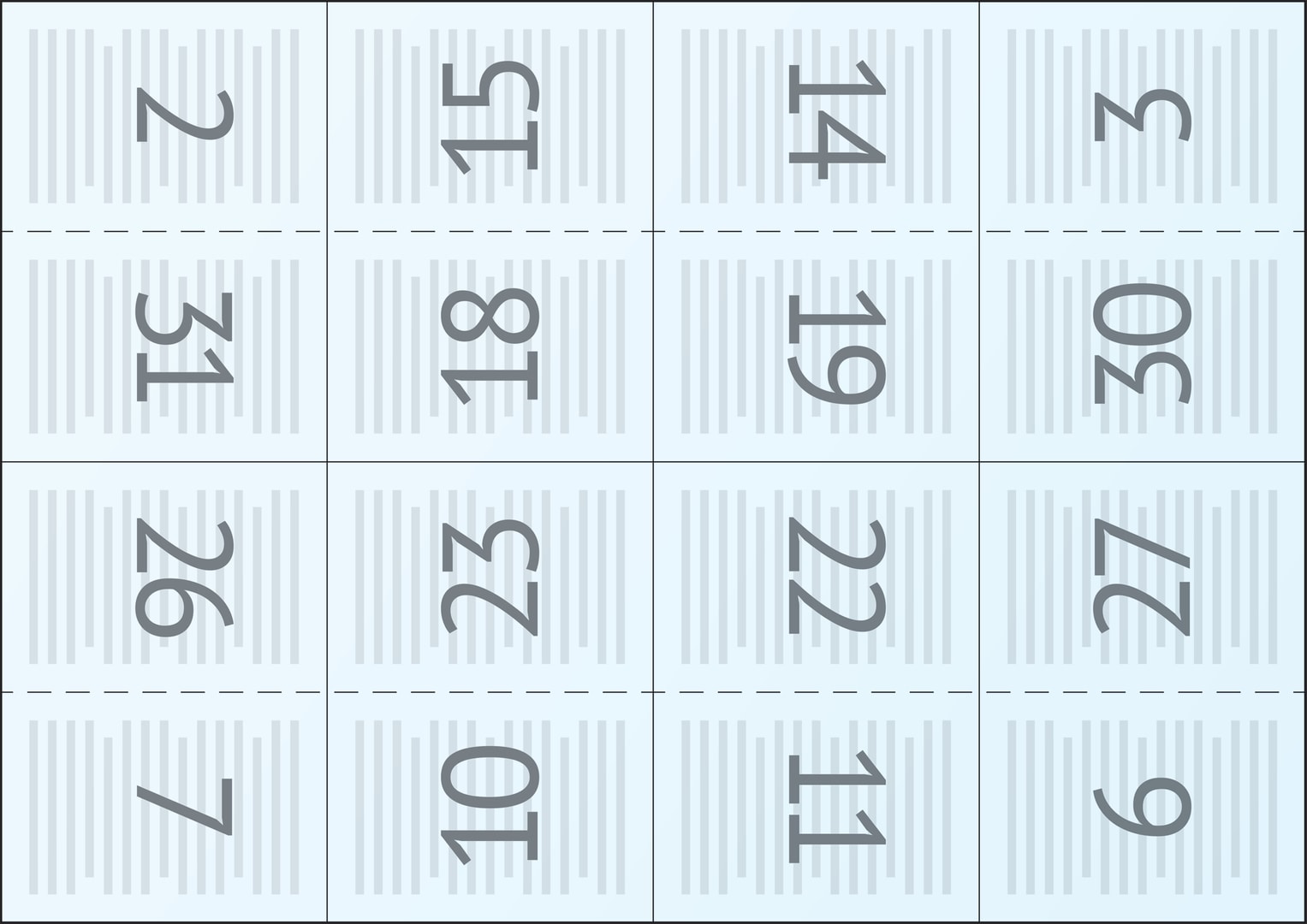
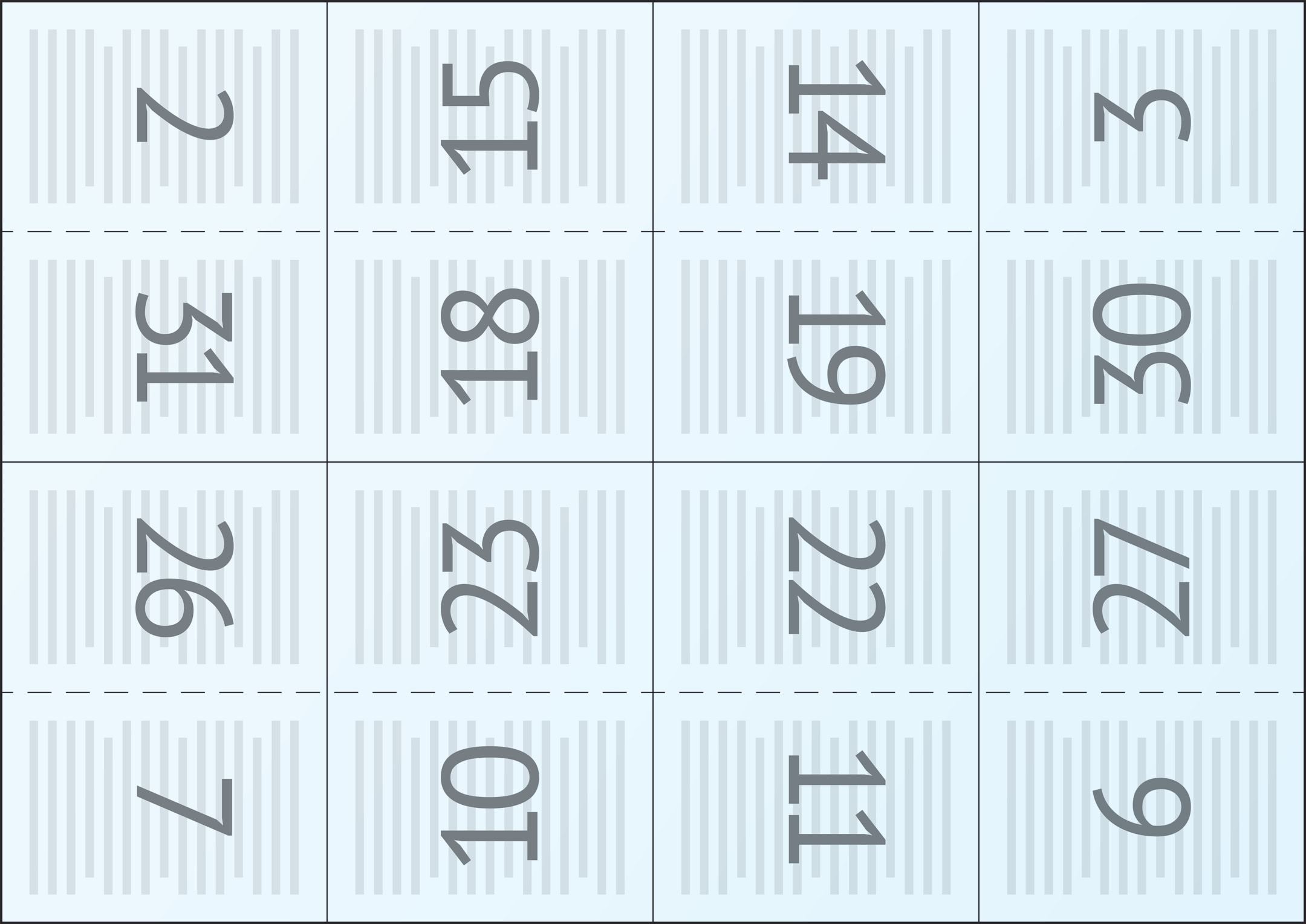
С каж­дой из двух сто­рон лист делится на 16 частей, каж­дая «ячейка» — будущая стра­ница книги. После печати лист скла­ды­ва­ется несколько раз и пре­враща­ется в тет­радь из 32 стра­ниц.

Один из спо­со­бов сво­ра­чи­ва­ния листа в тет­радь пояс­няют рисунки, на кото­рых пред­став­лены обе сто­роны листа. Само слово тет­радь про­ис­хо­дит от древ­негре­че­ского τετράς (четыре), воз­никло оно с раз­ви­тием письма и книж­но­сти, его язы­ко­вой род­ствен­ник — тет­раэдр.

Тет­ради под­би­раются в книгу, затем про­ис­хо­дит обрезка блока книги. Иногда обрезка про­ис­хо­дит неак­ку­ратно, неко­то­рые стра­ницы остаются нераз­ре­зан­ными. В преж­ние времена выраже­ние «нераз­ре­зан­ная книга» озна­чало, что она оста­лась непро­чи­тан­ной.

После обрезки размеры листов книги несколько уменьшаются и для нашей книги полу­чаются зна­че­ния 165 мм и 235 мм (чуть меньше, чем «тео­ре­ти­че­ские» 175 мм и 250 мм). При­чём если стра­ницы книги соеди­нены клеем, то обрезка про­из­во­дится не по трём, а по всем сто­ро­нам. В этом слу­чае размеры стра­ницы ста­но­вятся ещё меньше.

Сде­лаем несколько общих заме­ча­ний.

В соот­вет­ствии со стан­дар­тами, как размеры типограф­ского листа, так и коли­че­ство долей, на кото­рые он делится, могут быть и другими. Напри­мер, $70\times 90  ^1\!/\!_{32}$, $84\times 108  ^1\!/\!_{32}$, $60\times 84  ^1\!/\!_{8}$. Знаме­на­тель дроби, опре­де­ляющей долю, можно по-раз­ному рас­кла­ды­вать на множи­тели, каж­дое раз­ложе­ние даёт свой спо­соб деле­ния сто­рон листа. «Пре­имуще­ством» поль­зуются раз­ложе­ния, близ­кие к зна­че­нию корня из знаме­на­теля: для 32 — $4\times 8$, для 24 — $4\times 6$.

Раньше под­борка тет­ра­дей в книгу про­ис­хо­дила вруч­ную. Для облег­че­ния этой работы на пер­вой стра­нице каж­дой тет­ради внизу были напе­ча­таны номер тет­ради и фами­лия автора, на тре­тьей — номер тет­ради и знак *. Пер­вое ука­за­ние — поря­док компо­новки тет­ра­дей, вто­рое — для про­верки пра­виль­но­сти компо­новки внутри одной тет­радки.