В 1920 и 1921 годах над малоэтажным в то время районом Шаболовки вырастала удивительная по красоте башня, причём росла «сама по себе» — рядом не было ни кранов, ни лесов. Сейчас эта 150‐метровая башня, построенная по проекту Владимира Григорьевича Шухова, — один из узнаваемых архитектурных символов Москвы.
Дневник В. Г. Шухова сохранил для нас математические расчёты по проекту. Конструкция состоит из шести секций-гиперболоидов, каждая секция — «паутина», образованная прямыми стальными швеллерами, расположенными по образующим гиперболоидов.
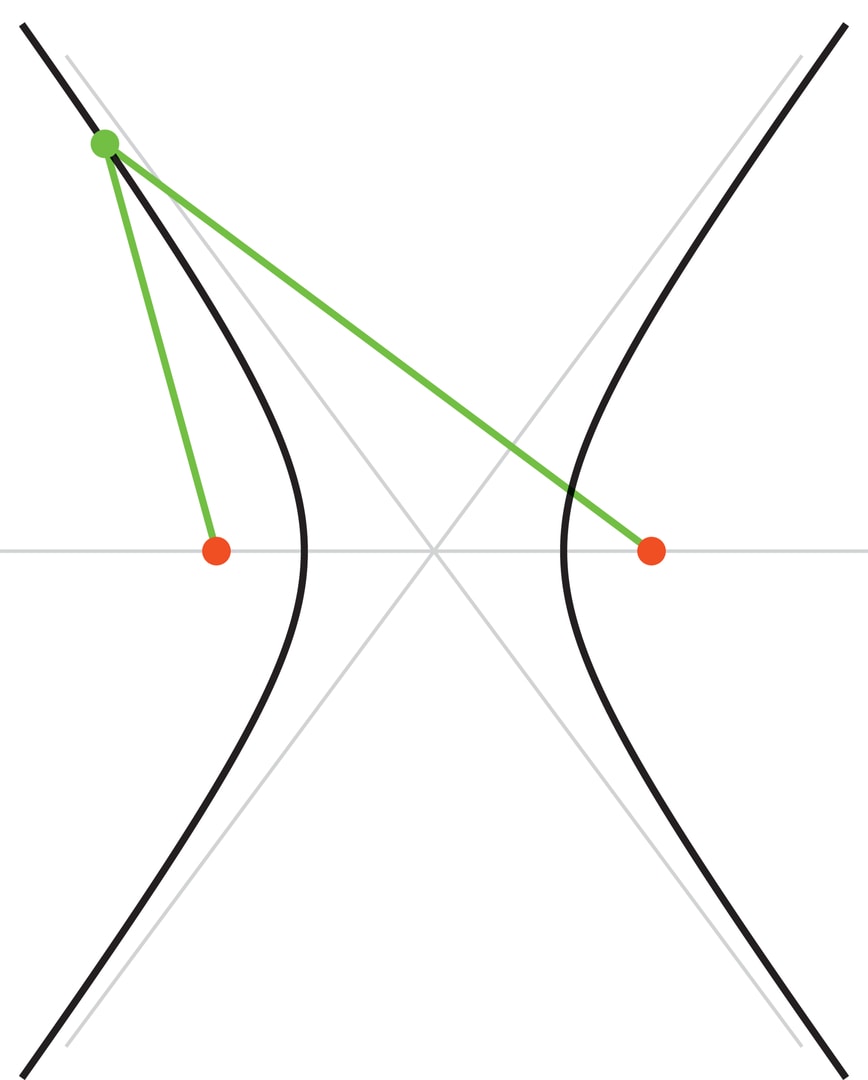
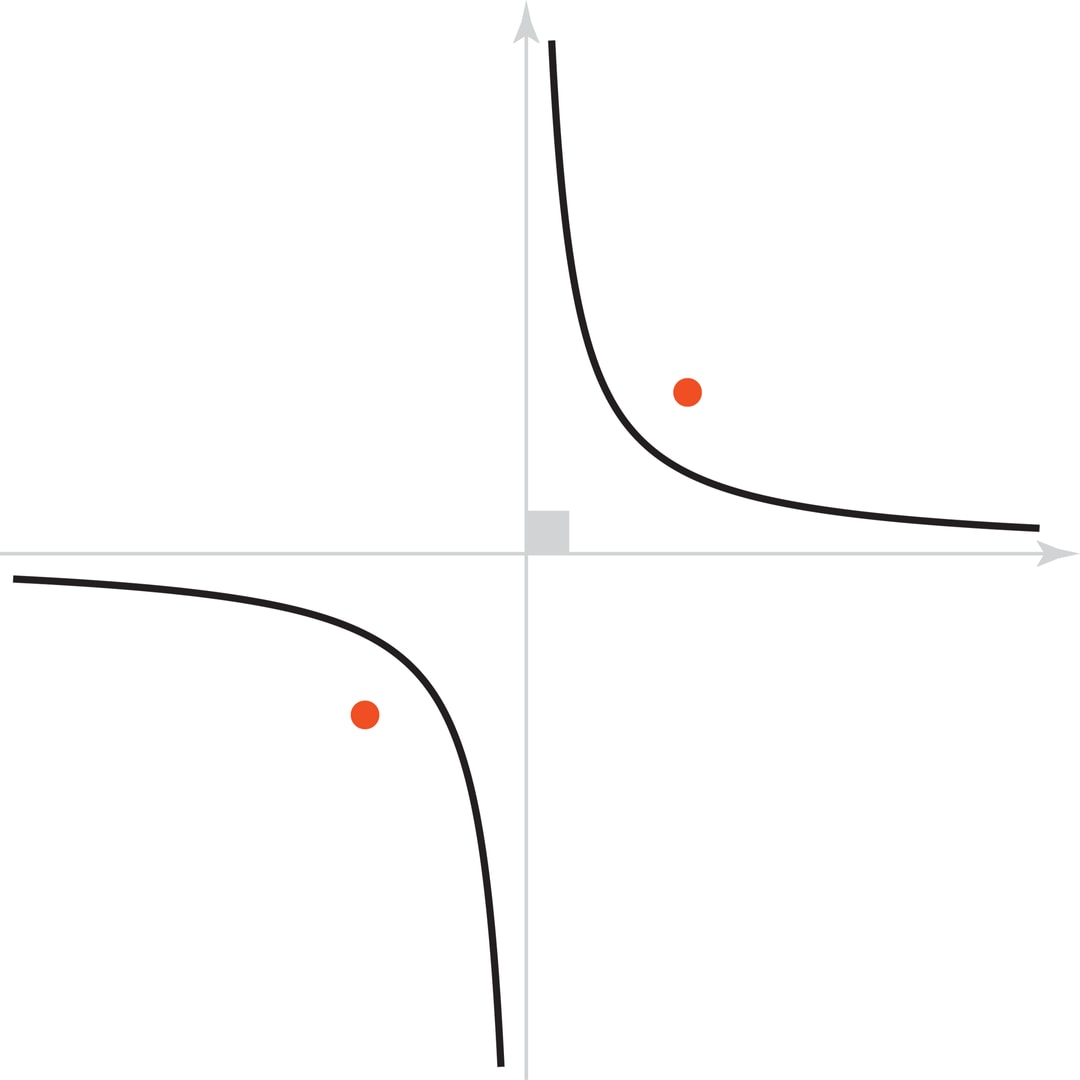
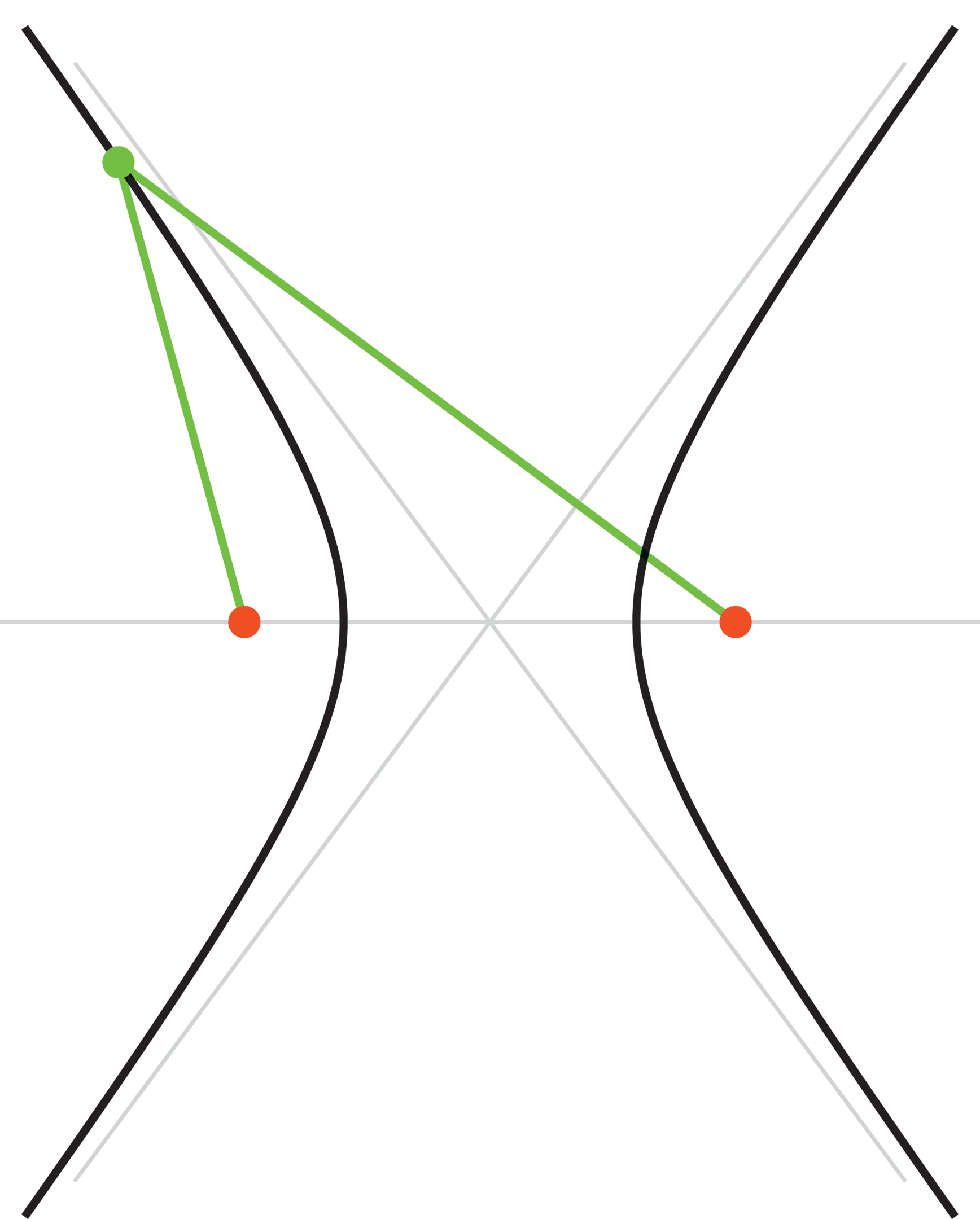
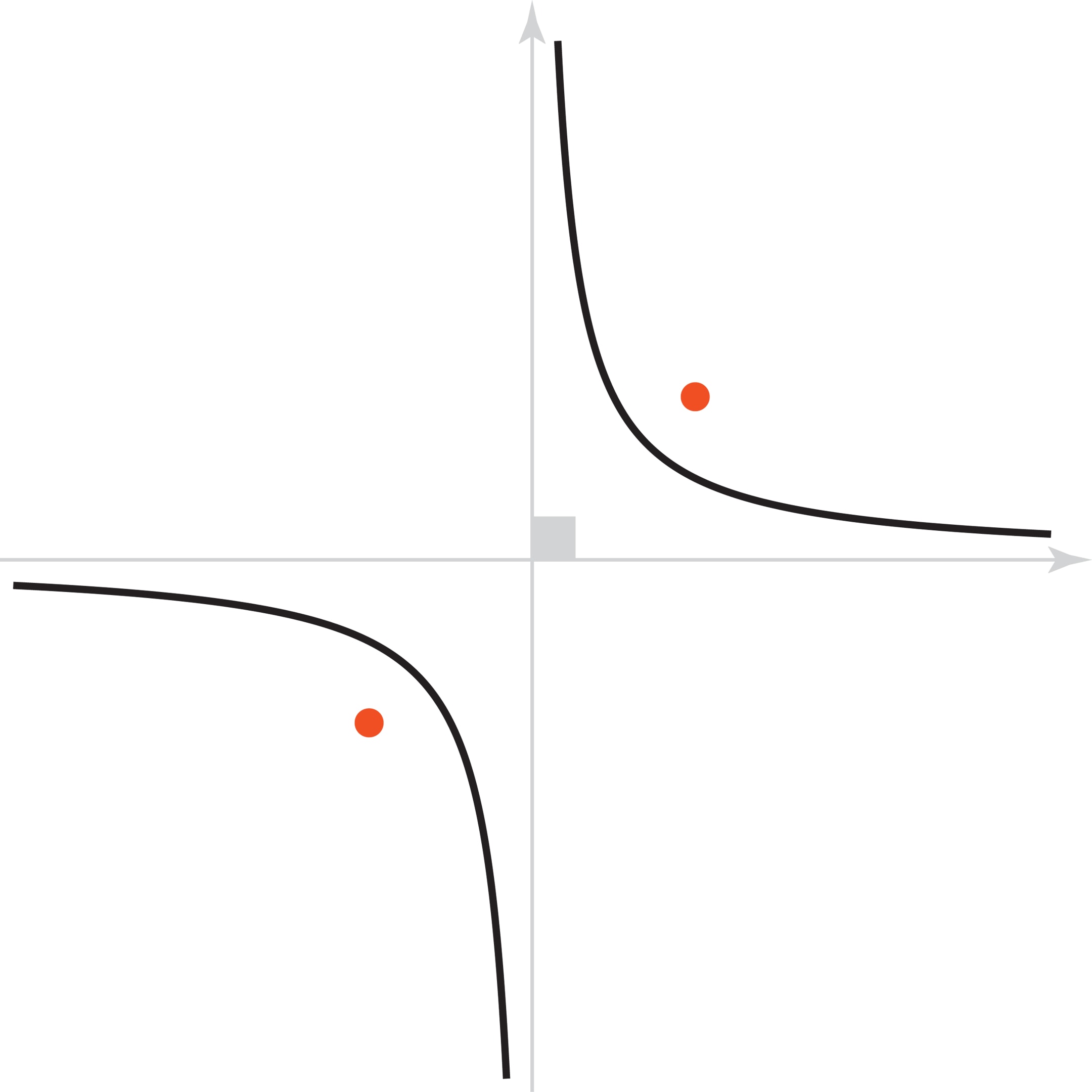
Гипербола — кривая на плоскости, модуль разности расстояний от любой точки которой до двух данных, называемых фокусами, постоянен. Гипербола является коническим сечением, наряду с эллипсом и параболой, но отличается от них тем, что у неё есть асимптоты — прямые, к которым она приближается, но никогда их не достигает. У изучаемой в школе гиперболы $y=1/x$ асимптоты перпендикулярны друг другу и совпадают с осями декартовой системы координат.
При вращении гиперболы вокруг её оси симметрии, перпендикулярной отрезку с концами в фокусах, получается поверхность — однополостный гиперболоид вращения.
Оказывается, что через каждую точку гиперболоида проходят две прямые, полностью лежащие на нём. Каждая из них при вращении вокруг оси гиперболоида «заметает» всю поверхность. Такие линии называются образующими. Образующие делятся на два семейства: в одно семейство попадают те образующие, которые при вращении вокруг оси переходят друг в друга. Соответственно и однополостный гиперболоид двумя способами можно представить как своеобразный «паркет», выложенный прямыми одного семейства.
Таким образом, изогнутая поверхность состоит из прямых. Именно это свойство и использовал В. Г. Шухов: каждая секция башни на Шаболовке «соткана» из образующих двух семейств.
В. Г. Шухов спроектировал и построил в России более двухсот гиперболоидных водонапорных башен. При этом каждый проект был уникален — выполнение технических требований соединялось с архитектурной привязкой к местности. А первая такая конструкция была представлена на Всероссийской промышленной и художественной выставке, проходившей в 1896 году в Нижнем Новгороде.
Ещё несколько известных примеров. Для перехода линии электропередачи НиГРЭС через Оку под Нижним Новгородом был сооружён каскад из четырёх пар гиперболоидных опор (самые высокие — по 128 метров). Под Херсоном до сих пор сохранились большой и малый маяки гиперболоидной конструкции.
За последние десятилетия в разных странах появилось несколько высотных гиперболоидных сооружений. И все их авторы признают огромный вклад, который внёс в разработку таких конструкций великий инженер и учёный Владимир Григорьевич Шухов.
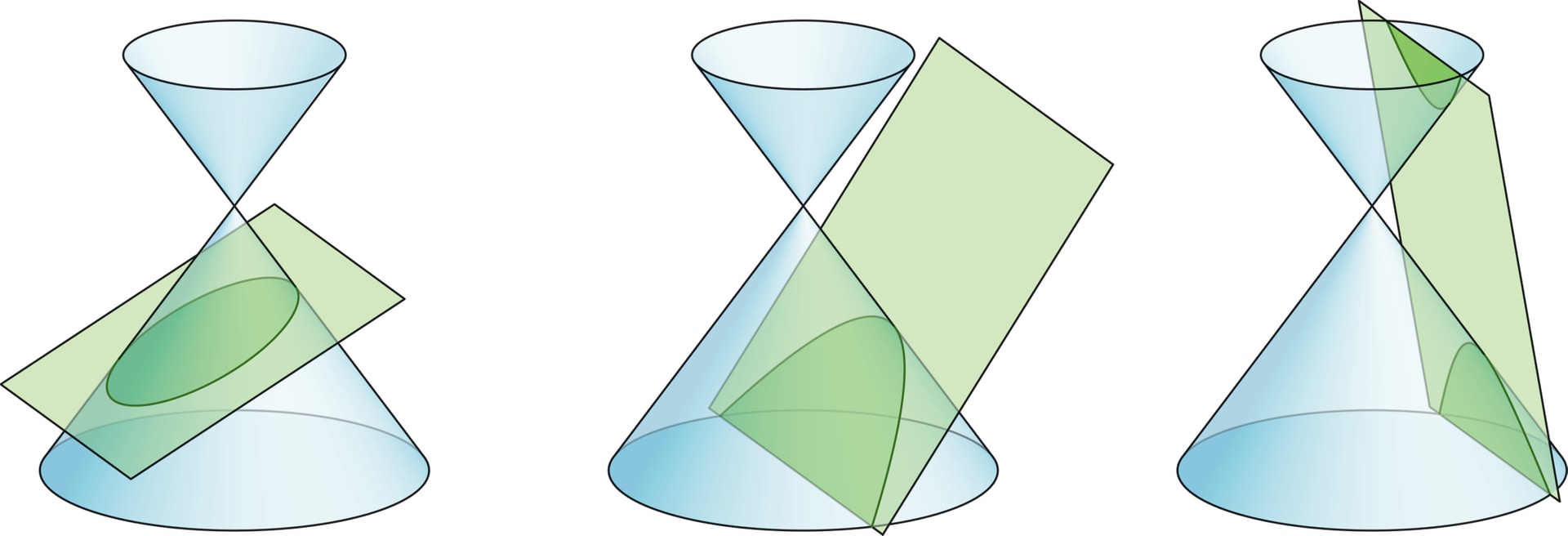
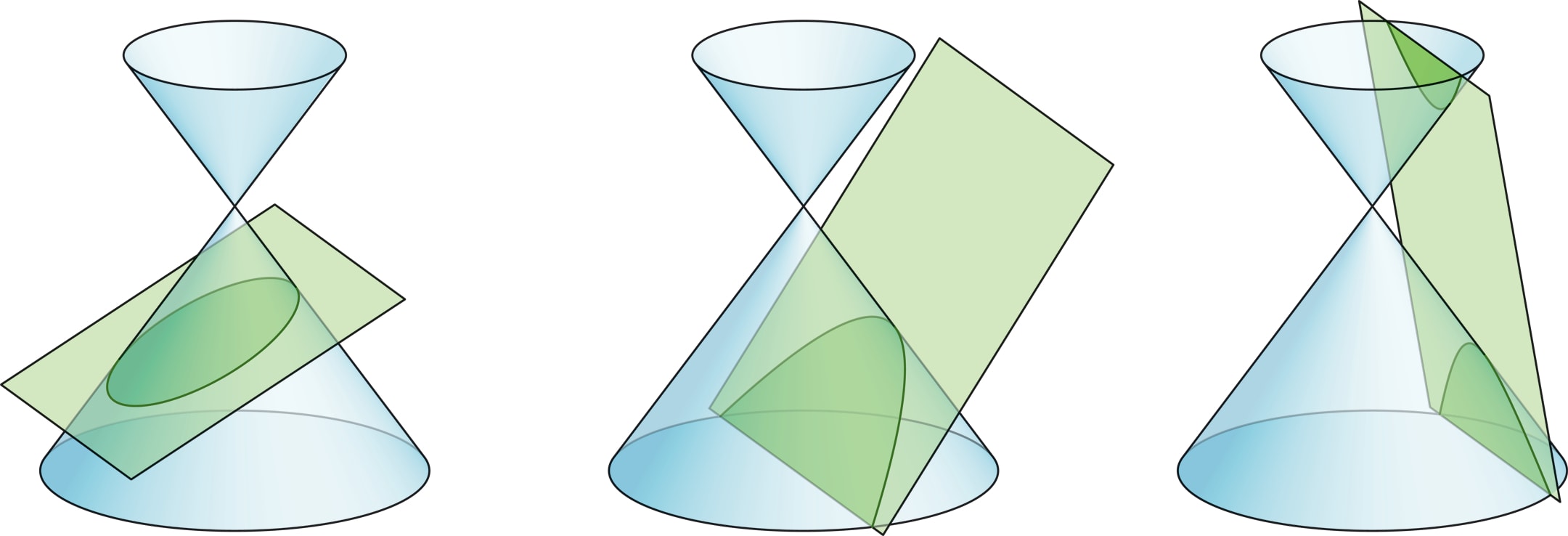
Это следует из определения гиперболы как конического сечения — так называется пересечение прямого кругового конуса (двустороннего, симметричного относительно вершины) с плоскостью.
Если плоскость пересекает все образующие конуса, то она пересекается только с одной его «половиной», получается эллипс (окружность). Парабола возникает, когда секущая плоскость параллельна ровно одной образующей (как следствие — пересекается только с одной половиной). Если секущая плоскость пересекает обе половины конуса (иначе говоря, параллельна двум образующим), то это гипербола. В частности, так происходит, если плоскость параллельна оси конуса (в примере — грифелю карандаша).
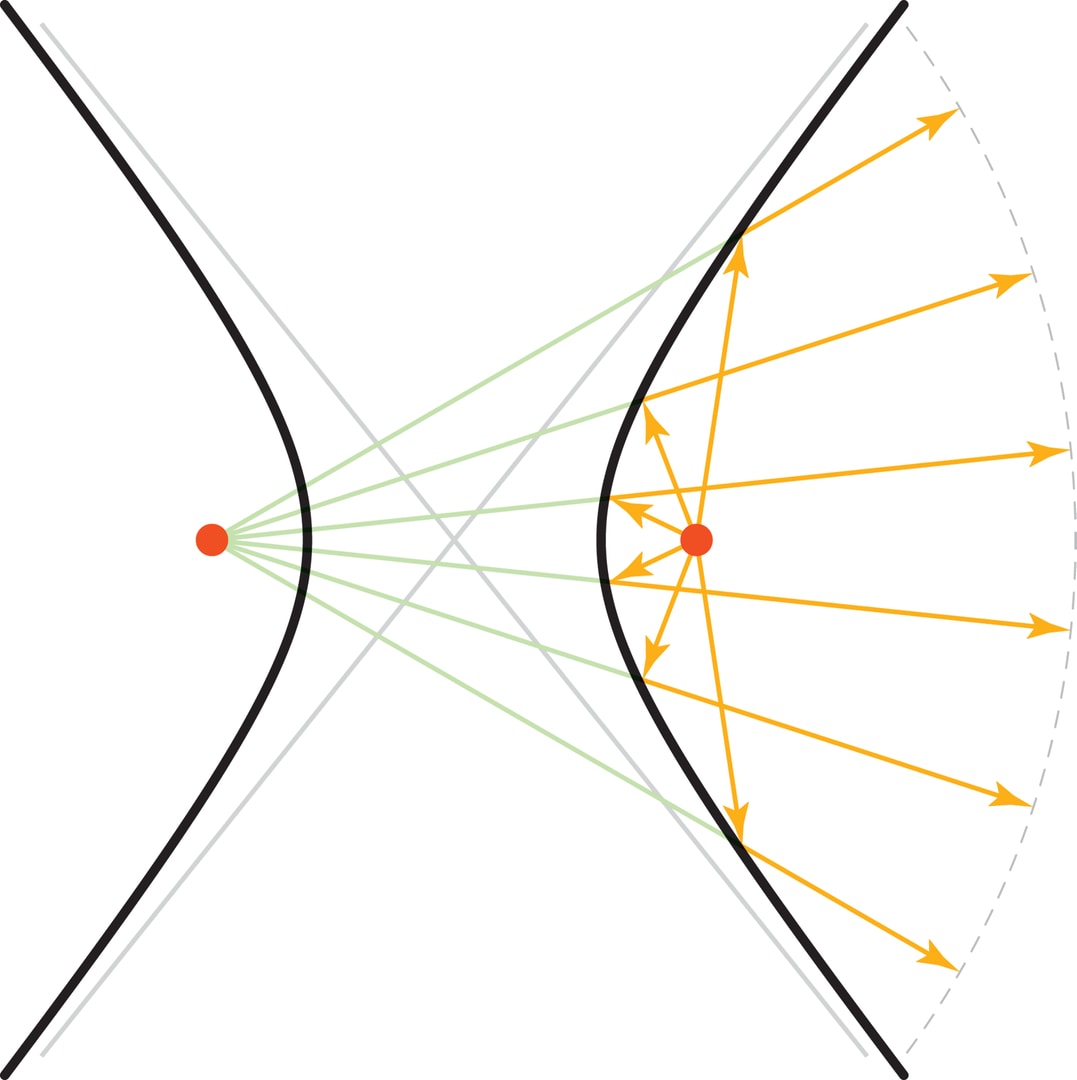
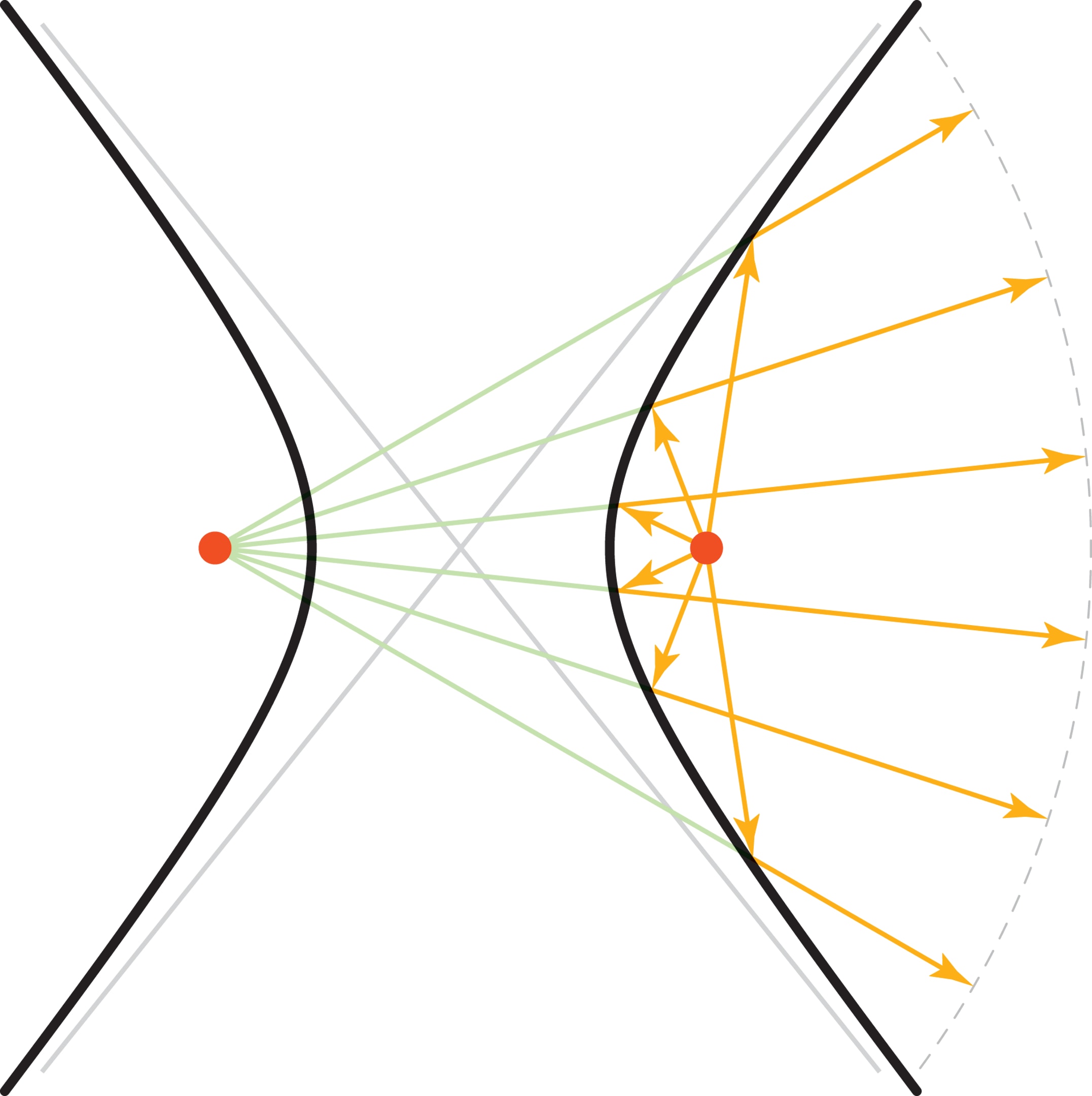
Оптические свойства эллипса и параболы оказались весьма полезными рабочими инструментами (см. «Дробление камней в почках» и «Параболическая антенна»). У гиперболы тоже есть оптическое свойство: лучи, вышедшие из одного фокуса гиперболы, после отражения от гиперболического зеркала (ближайшая ветвь гиперболы) уходят по направлению вектора, идущего от второго фокуса к точке отражения. Передний фронт отражённых лучей будет окружностью с центром во втором фокусе (это непосредственно следует из геометрического определения гиперболы). На оптическом свойстве гиперболы основана оптическая схема Ричи—Кретьена рефлекторных телескопов с гиперболическими зеркалами. К этому типу относится большинство научно-исследовательских телескопов. Наиболее известные примеры: космический Hubble; наземный VLT (Very Large Telescope) — система телескопов на горе Серро-Параналь в Чили с самыми большими в мире монолитными зеркалами (диаметр каждого — 8,2 метра, толщина — 177 мм, масса — 22 тонны).
Наличие особой «оптической» точки — фокуса — характеристическое свойство конических сечений. Исходящие из фокуса лучи после отражения от линии превращаются в сходящийся, расходящийся или параллельный пучок, в зависимости от того, чем является зеркало — эллипсом, гиперболой или параболой.
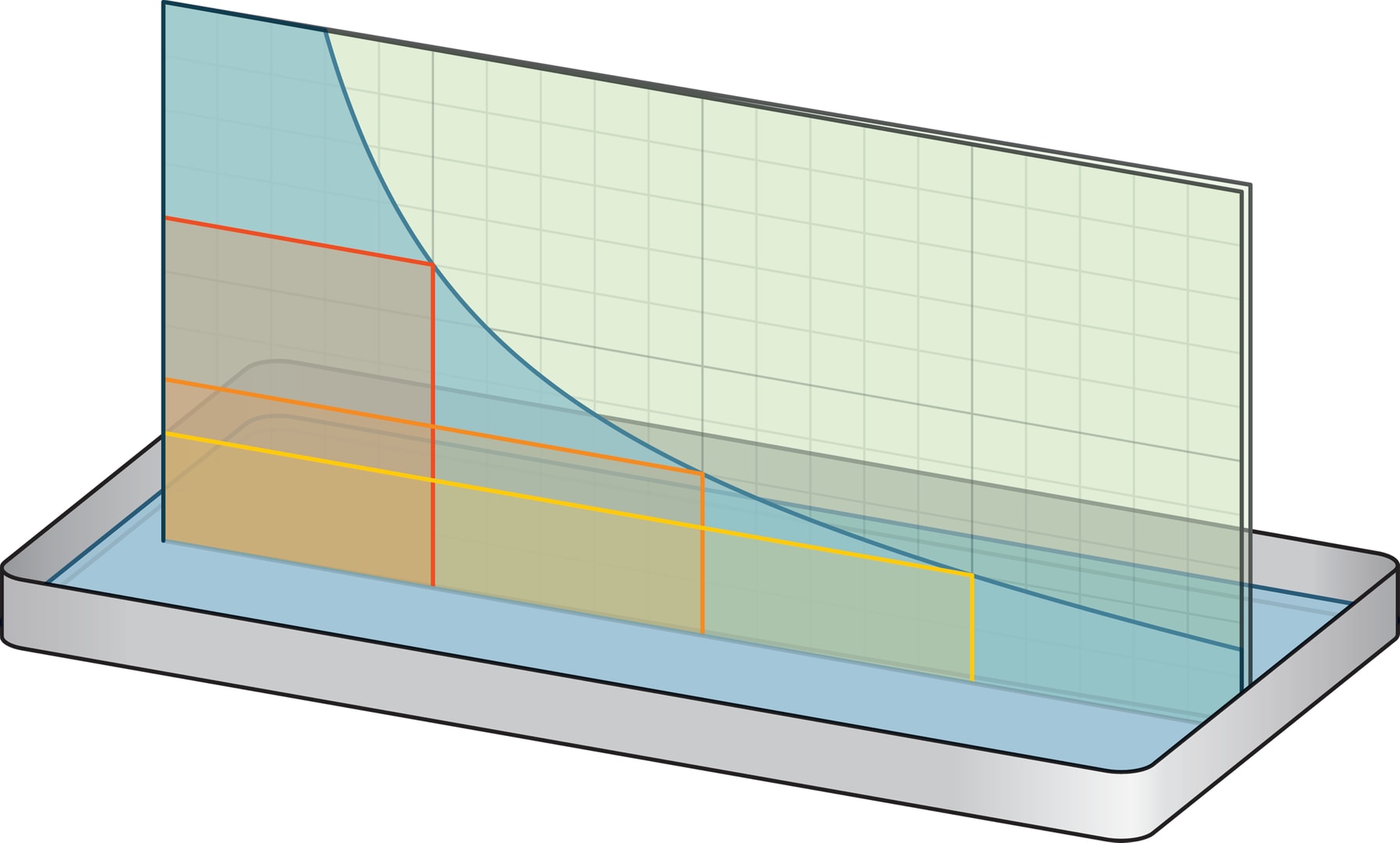
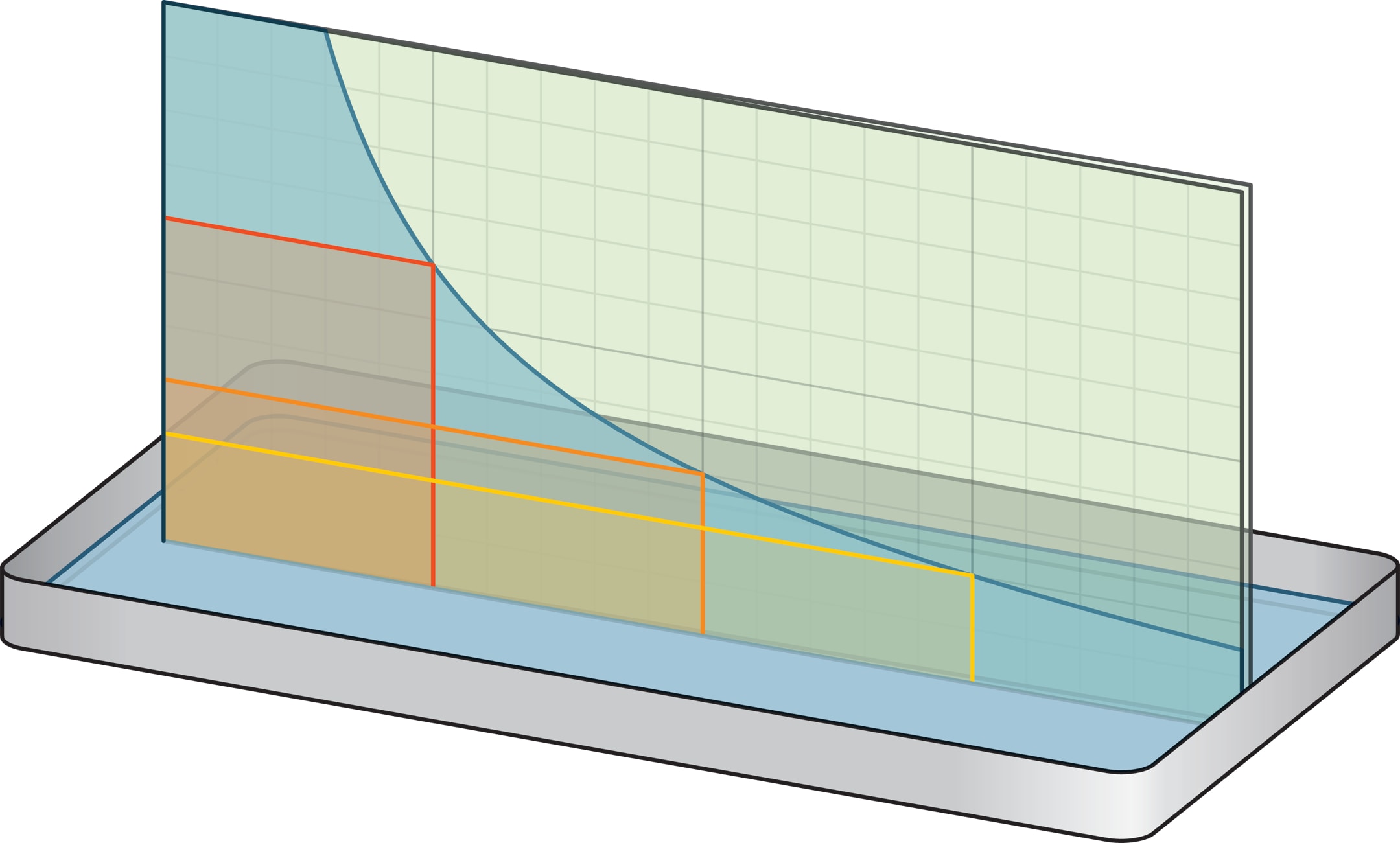
Гиперболу в домашних условиях могут «нарисовать» силы поверхностного натяжения.
В ванночку с водой поставьте две прямоугольные стеклянные пластинки в виде слегка приоткрытой книги. Начните медленно закрывать «книгу»: вода между пластинками поднимется, а её уровень будет снижаться по знакомой кривой — гиперболе (начинающейся с некоторым отступом от «корешка»). Если предварительно на одном стёклышке нарисовать мелкую квадратную сетку, то можно проверить, что получилась именно гипербола: площади прямоугольников под линией будут одинаковыми.
Физическое объяснение описанного эксперимента читатель может получить самостоятельно, а может найти в журнале «Квант» (№ 11 за 1973 год, стр. 32, 33).
Прочность гиперболоидных конструкций обоснована инженерными расчётами и проверена на практике. В первоначальном плане В. Г. Шухова по возведению башни в Москве предполагалось, что башня будет выше Эйфелевой на 50 метров, но при этом вчетверо легче! Несминаемость тумб такой конструкции испытана в цирках: лёгкие, ажурные тумбы выдерживают даже слонов. Одно из неземных применений — крепления, соединяющие ступени космических ракет: это тоже решётки из образующих однополостного гиперболоида.
Первая в мире гиперболоидная конструкция уцелела и стоит сейчас в селе Полибино Липецкой области. После завершения работы Всероссийской выставки в Нижнем Новгороде башню Шухова выкупил меценат Юрий Нечаев-Мальцов и установил в своём имении.
Кроме башни на Шаболовке, в Москве и её окрестностях сохранились гиперболоидные водонапорные башни в Лобне (микрорайон Луговая) и в посёлке Николина Гора.
В Нижегородской области сохранилась (и отреставрирована) одна из двух 128‐метровых опор каскада линии электропередачи НиГРЭС (недалеко от города Дзержинска). Также гиперболоидные конструкции Шухова можно увидеть в деревне Ляхово, в городе Выкса, да и в самом Нижнем Новгороде (район Копосово, улица КИМа).
Большой Станислав-Аджигольский маяк под Херсоном является самой высокой гиперболоидной секцией среди спроектированных Шуховым. До сих пор это самый высокий маяк Украины.
Сохранившиеся гиперболоиды Шухова можно увидеть и в других городах: Белая Церковь (Украина), Борисов (Республика Беларусь), Бухара (Республика Узбекистан), Вологда, Казань, Конотоп (Украина), Коханово (Республика Беларусь), Краснодар, Кукмор, Николаев (Украина), Петушки, Черкассы (Украина).
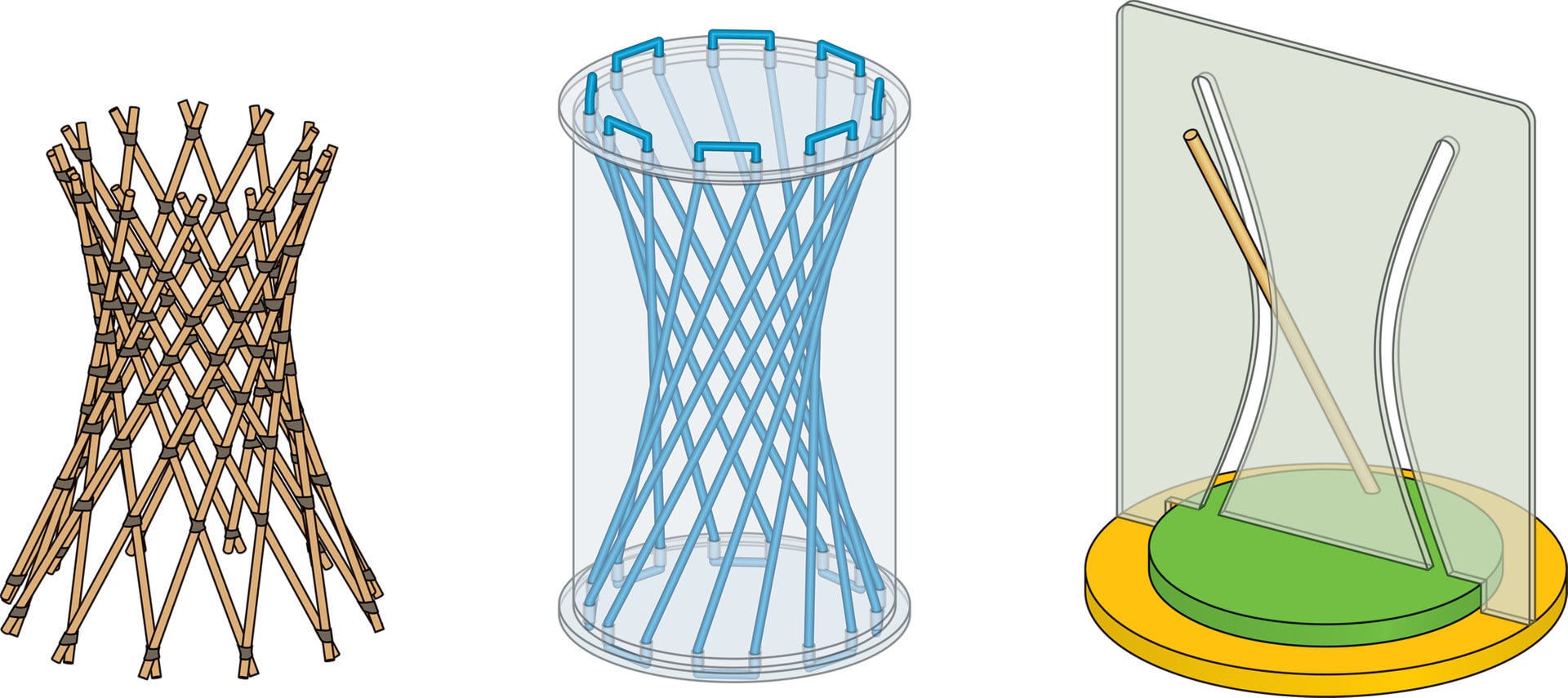
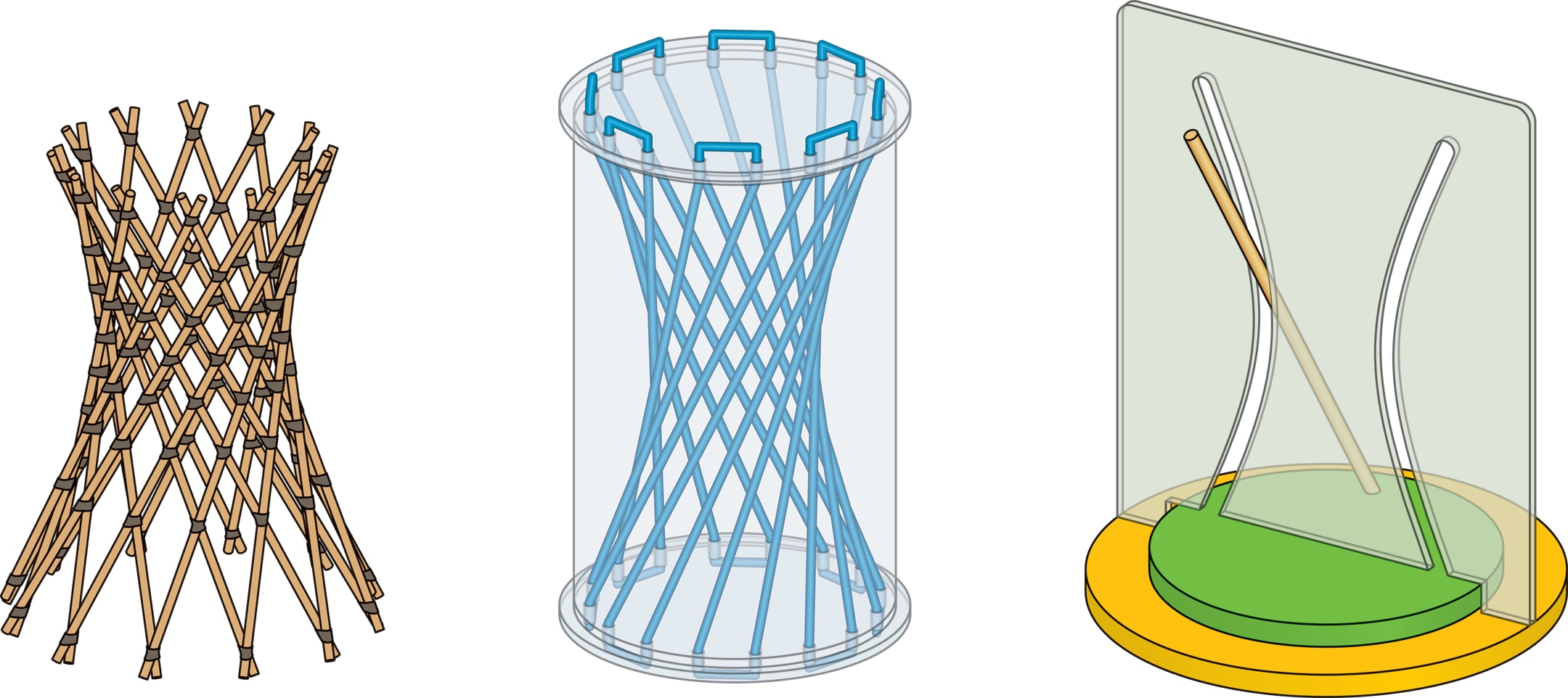
Настольную модель гиперболоидной башни Шухова можно сделать своими руками. Тонкие деревянные палочки (например, шпажки для шашлыка) и соединительные кольца (резиновые или пластиковые) — вот всё, что вам понадобится. Правда, придётся поэкспериментировать, продумывая последовательность сборки. Можно изготовить и симметричный вариант, и вариант, в котором центр гиперболоида не совпадает с серединой модели. В данной модели представлены оба семейства образующих — в точности как в конструкциях Шухова. Все модели можно «раздувать», получая гиперболоиды разных размеров.
Модель однополостного гиперболоида, в которой образующие — это резиновые нити, а не жёсткие палочки, также проста в изготовлении. Прозрачный полый цилиндр и его основания сделаны из пластика. Через равномерно расположенные на краях оснований небольшие отверстия челночно пропускается резиновая нить, которая притягивает основания, но позволяет вращать их вокруг оси цилиндра. При вращении оснований нити растягиваются и превращаются в образующие одного семейства, возникает контур гиперболоида.
В самой эффектной модели прямолинейная спица закреплена наклонно на вращающемся основании. При вращении основания вокруг центра спица проходит беспрепятственно через прорези в форме двух ветвей гиперболы, сделанные в неподвижной стенке. В этой модели подчёркнуто то, что однополостный гиперболоид — поверхность вращения, которую можно получить, вращая вокруг оси и гиперболу, и одну из образующих (прямую, скрещивающуюся с осью).
О происхождении и значении термина «фокус», о гиперболе как огибающей семейства прямых и о том, как получить гиперболу в виде муарового узора, см. комментарии к статье «Параболическая антенна».
Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2‐е изд. — М.: Наука, 1978. — [Ко 2‐му изданию книга была значительно переработана и дополнена, с тех пор переиздавалась несколько раз].
Маркушевич А. И. Замечательные кривые. — М.—Л.: ГИТТЛ, 1952. — (Популярные лекции по математике; Вып. 4).
Арнольд В. И. Математическое понимание природы. — М.: МЦНМО, 2010. — [Сюжет «Резонансы в Шуховской башне, в уравнении Соболева и в баках вращающихся ракет», стр. 131].
В. Г. Шухов: 1853—1939: Искусство конструкции. — М.: Мир, 1994.
Металлические конструкции академика В. Г. Шухова. — М.: Недра, 1990.
Шухова Е. М. Владимир Григорьевич Шухов: Первый инженер России. — М.: МГТУ имени Н. Э. Баумана, 2003.
В. Г. Шухов — выдающийся инженер и учёный
Виноградова Т., Авдеев С. Код Шухова. — Нижний Новгород: Покровка‐7, 2013.
Зеленова С. В., Виноградова Т. П., Коротаева Д. И., Ометова Г. Н. В. Г. Шухов: нижегородские проекты. Территория уникальных объектов. — Нижний Новгород: Литера, 2016.
Архив РАН. Фонд Владимира Григорьевича Шухова. № 1508.
Ажурная башня
Конические сечения: гипербола