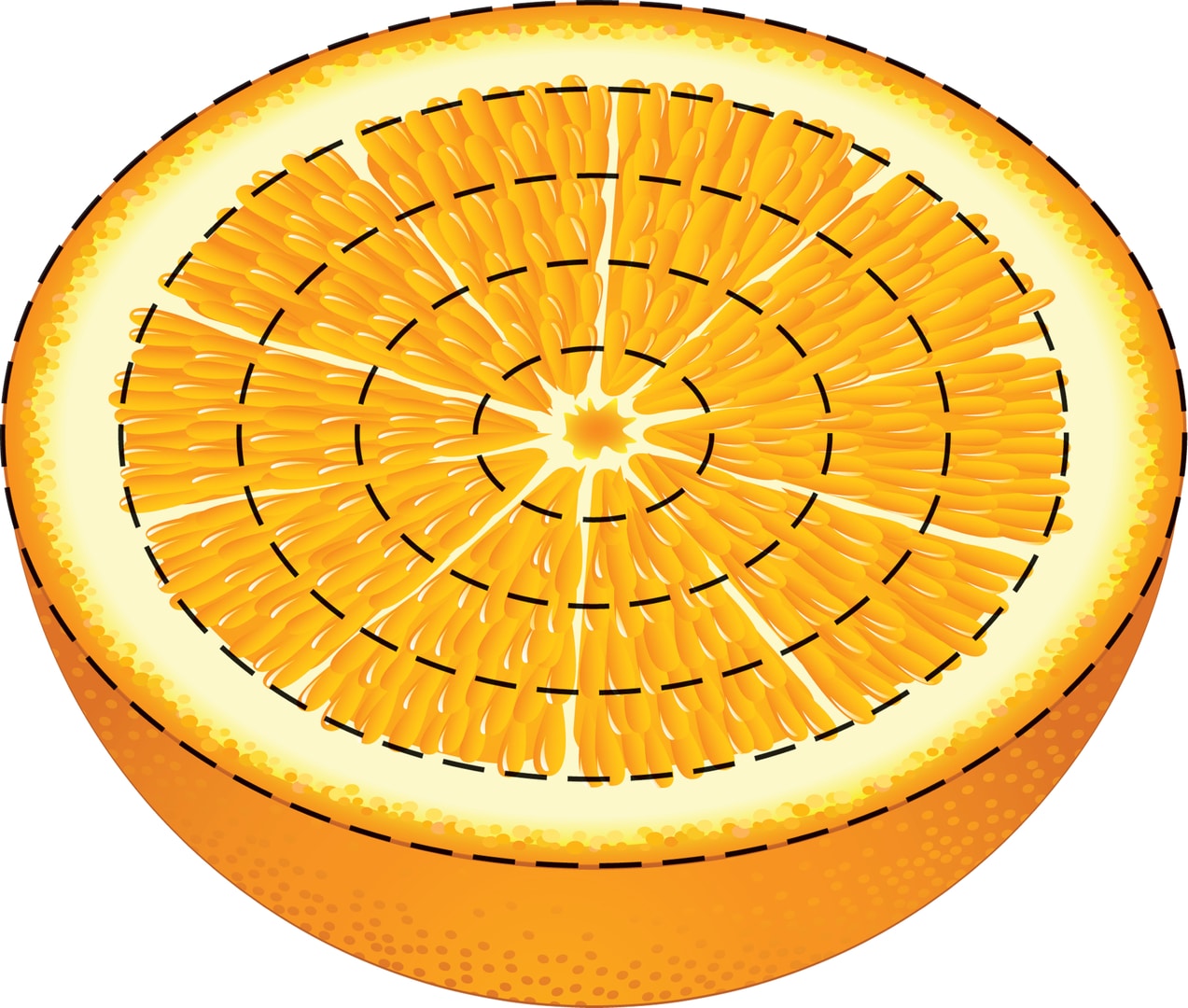
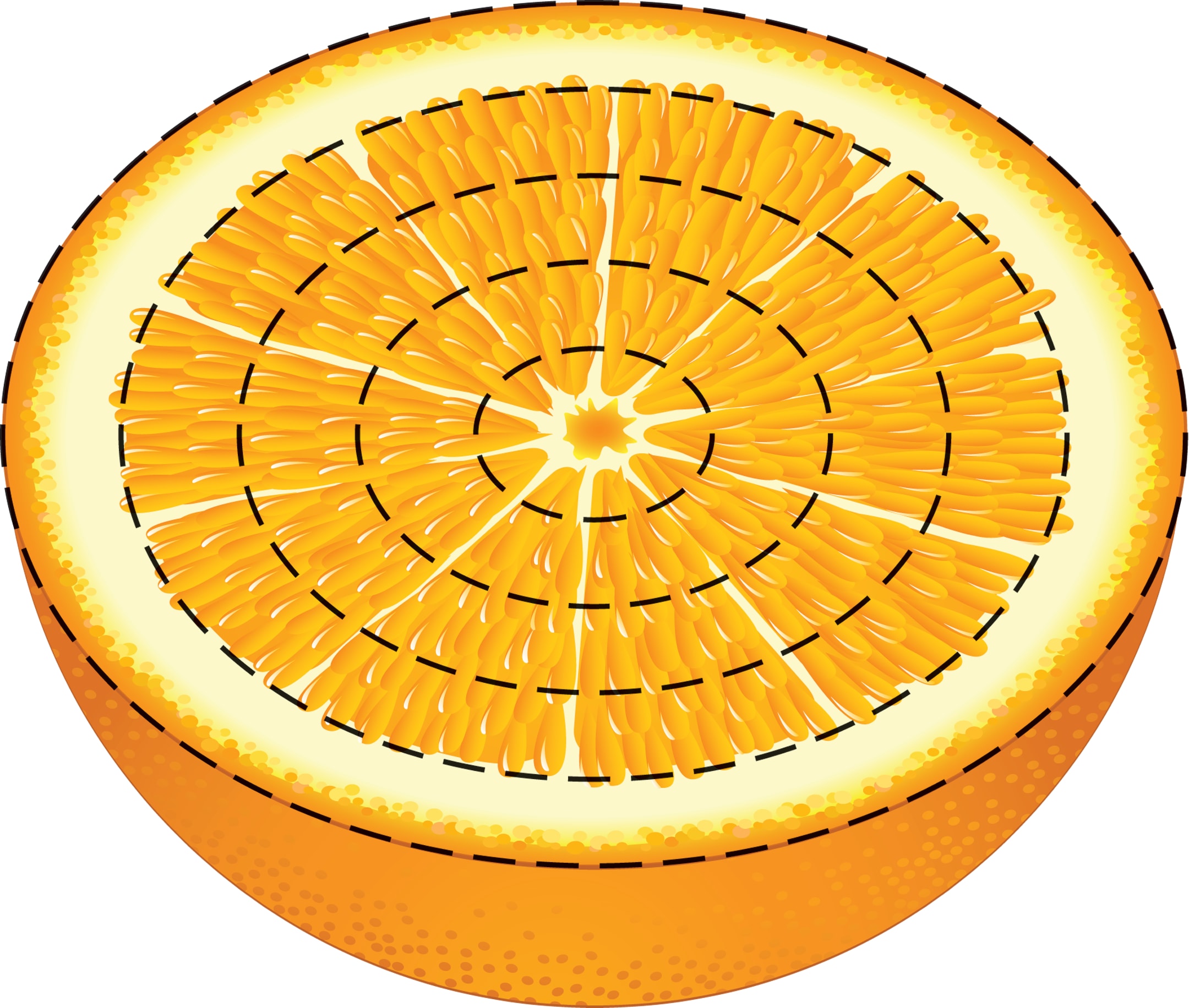
Вы купили апельсин и разрезали его пополам. Можно ли, глядя на половинку апельсина, определить, чего в ней больше — кожуры или мякоти?
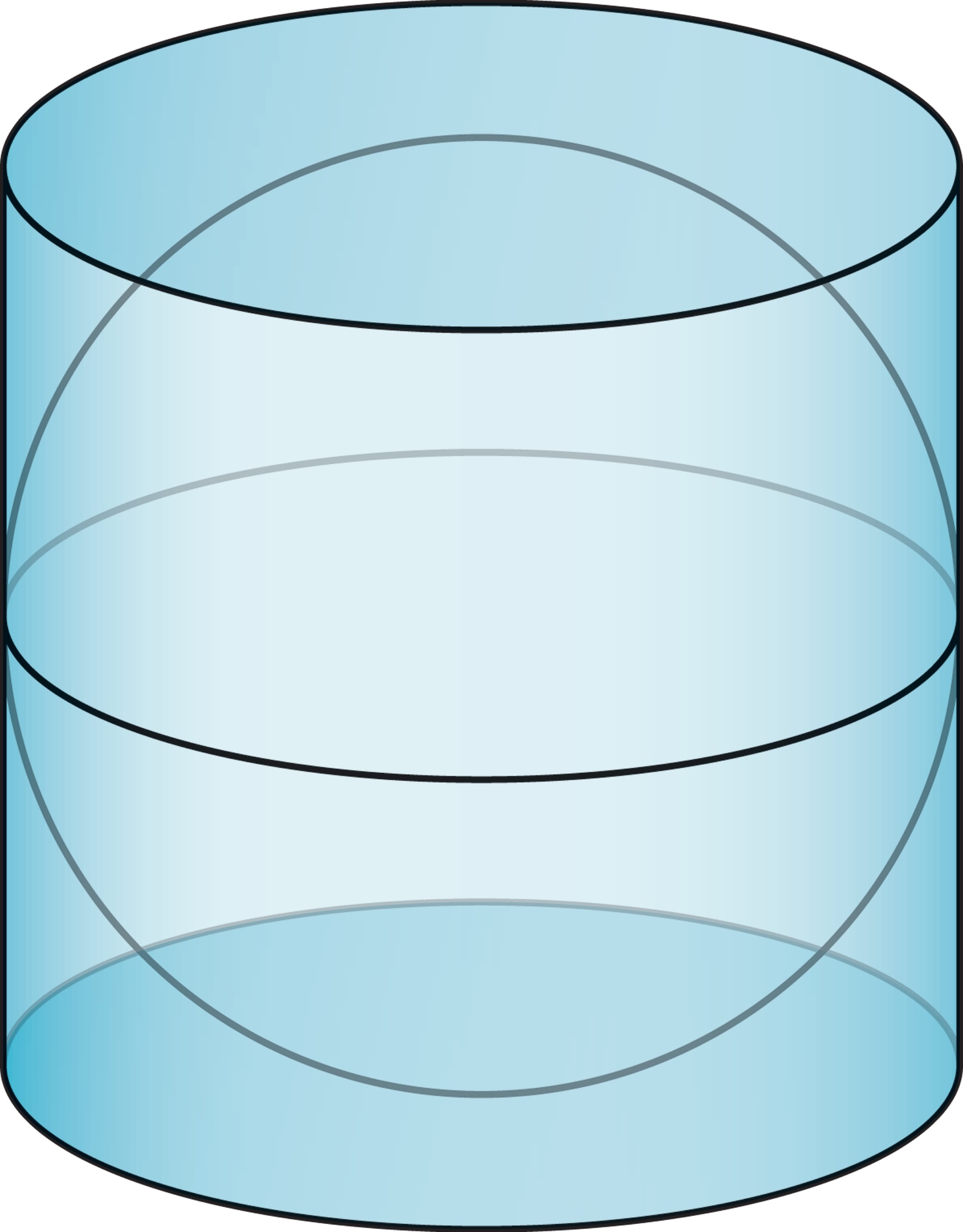
Вопрос кажется странным, ведь кожура — это тонкий слой, край апельсина (будем считать, что апельсин имеет форму шара). Оказывается, что относительно тонкий слой на границе шара имеет тот же объём, что и вся остальная часть. Например, у апельсина диаметром 10 см c кожурой толщиной 1 см почти половина всего объёма сосредоточена в кожуре!
Давайте проверим. Рассмотрим два шара радиусов $R$ и $r$ ($r<R$). Каким должен быть радиус меньшего шара, чтобы его объём составлял половину объёма большого?
Объём шара радиуса $R$ равен $V_R=\frac{4}{3} π R^3$. Для нахождения $r$ запишем уравнение $$ V_r=V_R-V_r, \;\;\; {\mathrm{или}} \;\;\; \frac{4}{3} π r^3 = \frac{4}{3} π R^3 - \frac{4}{3} π r^3 $$
Из него следует что $R^3=2r^3$, т. е. $$ r=\frac{R}{\sqrt[3]{2}} ≈ 0{,}79R ≈ \frac{4}{5} R. $$
Таким образом, почти половина объёма шара сосредоточена в слое около поверхности толщиной всего лишь $1/5$ радиуса.
В представленном на рисунке апельсине кожуры и мякоти поровну.
Поясним читателю выбор формы уравнения: $V_r=V_R-V_r$ вместо естественного $V_R=2V_r$. Это сделано, чтобы напомнить одну идею, часто встречающуюся в геометрии и полезную при решении житейских задач, — фигура, для площади или объёма которой нет готовой формулы, представляется как разность «известных» фигур.
Вычисление объёма и площади поверхности шара — результат Архимеда, который он считал своим высшим достижением. В сочинении «О шаре и цилиндре» Архимед писал:
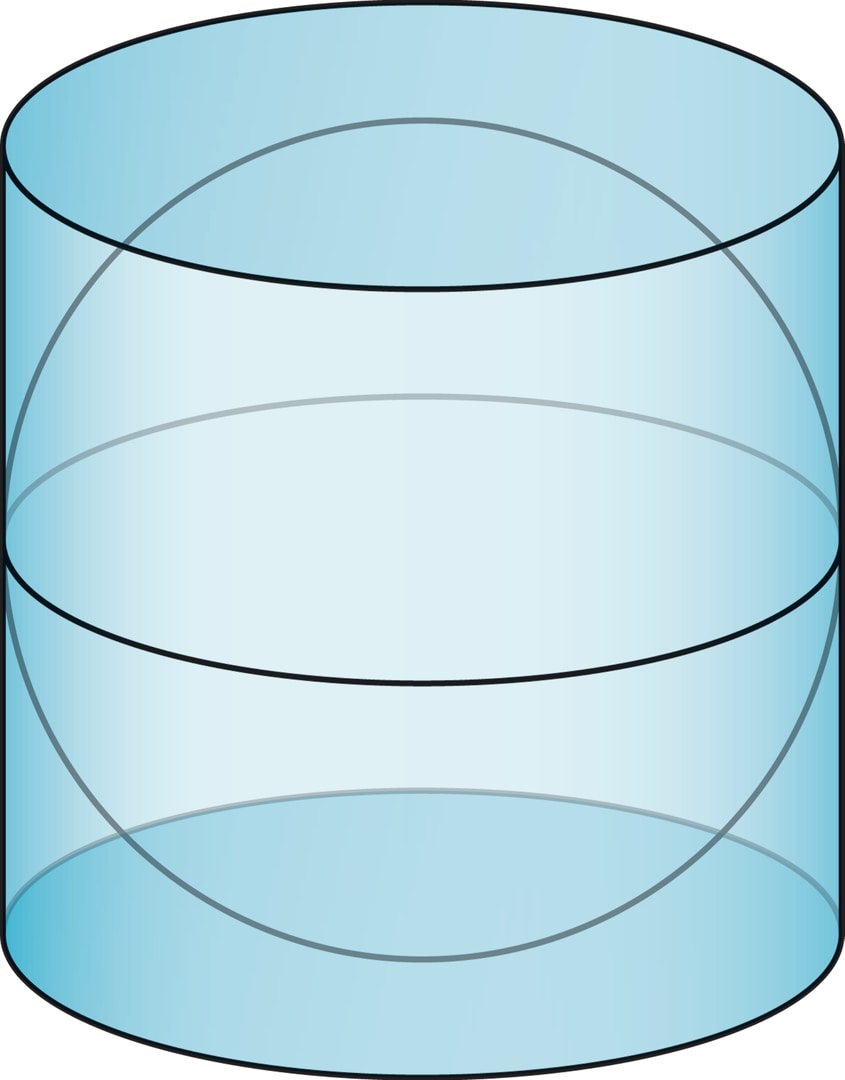
Архимед Досифея приветствует! Незадолго перед сим я препроводил к тебе некоторые предметы моих иcследований, вместе с найденными мною доказательствами […] Ныне я кончил и другие некоторые мне на мысль пришедшие теоремы, из коих достопримечательнейшие суть сии: […] Цилиндр, имеющий основанием наибольший круг шара, а высоту, равную поперечнику оного, есть полуторный шара; и его поверхность есть полуторная же поверхности шара. Свойства сии без сомнения существовали в сказанных фигурах, но доселе не были ещё замечены никем из занимавшихся Геометрией…
В формулах результат Архимеда для шара радиуса $R$ и описанного вокруг него кругового цилиндра имеет следующий вид: $$ V_{\mathrm{шара}}=\frac{4}{3}π R^3 \;\;\;\; \left(=\frac{2}{3}V_{\mathrm{цилиндра}}=\frac{2}{3}\cdot 2π R^3\right), $$ $$ S_{\mathrm{шара}}=4π R^2 \;\;\;\; \left(=\frac{2}{3}S_{\mathrm{цилиндра}}=\frac{2}{3}\cdot 6π R^2\right). $$
К моменту появления работы Архимеда и объём, и площадь цилиндра были уже известны.
Шар, вписанный в цилиндр, был изображён на надгробном памятнике у могилы учёного. Зная об этом, Цицерон, во время службы на Сицилии, смог найти могилу Архимеда и описал её в сочинении «Тускуланские беседы».
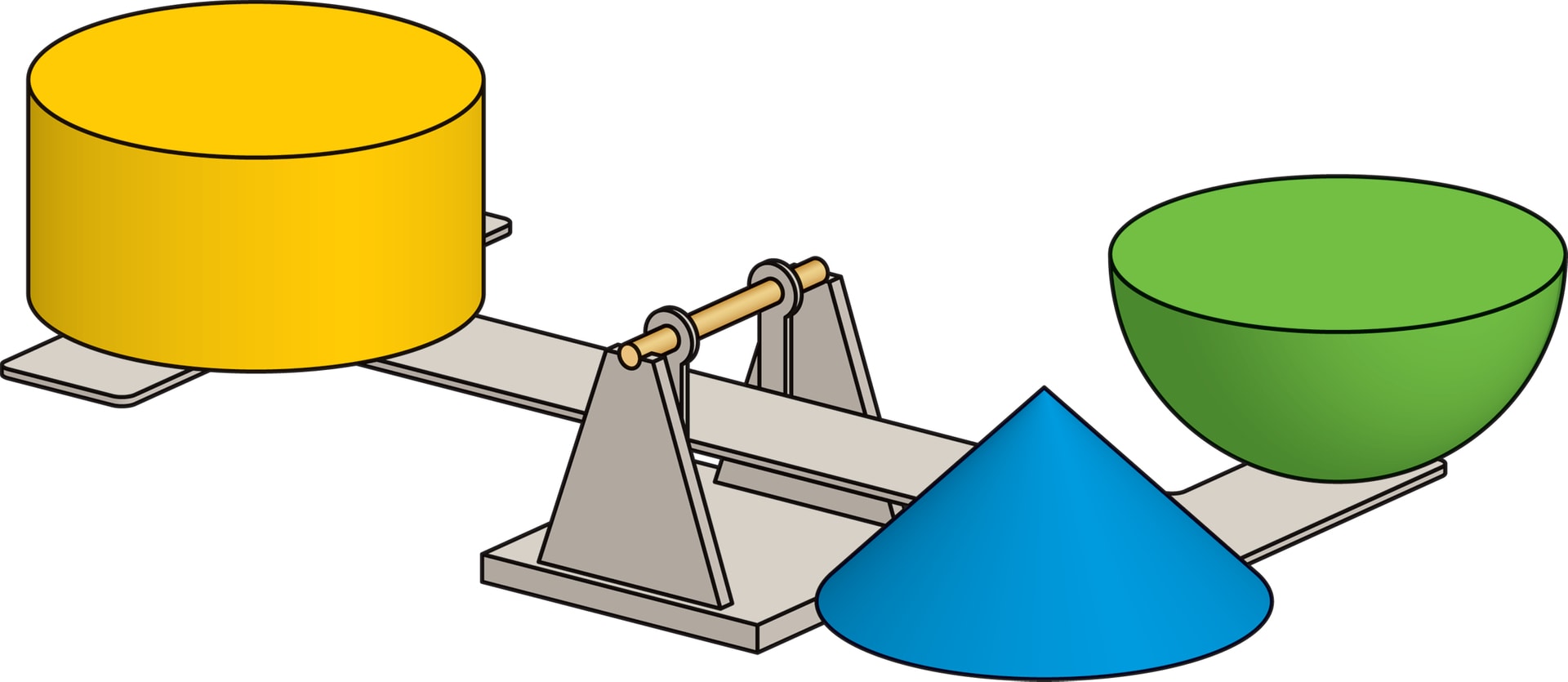
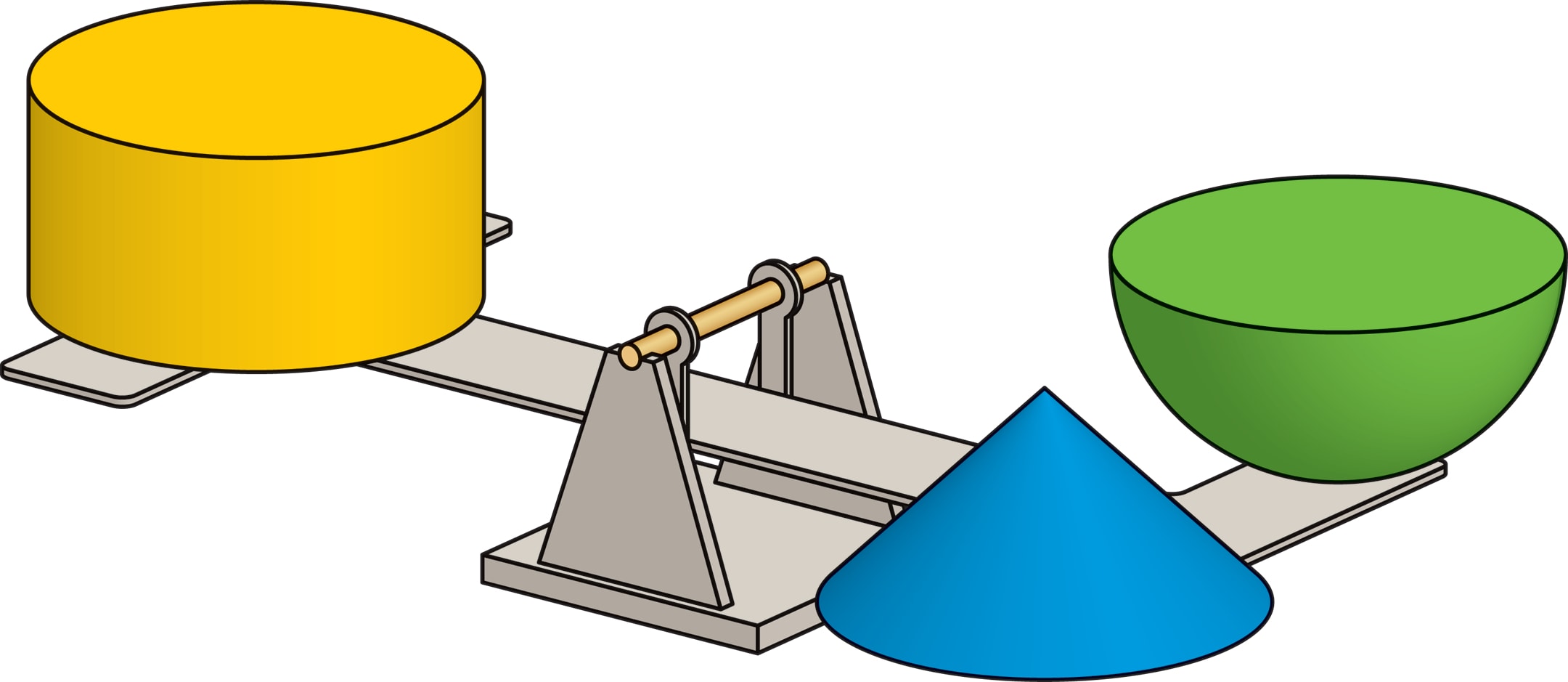
Идеи Архимеда можно продемонстрировать на модели, называемой «весы Архимеда». Рычажные весы будут в состоянии равновесия, если на равных расстояниях от подвеса установить: конус и половину шара — с одной стороны, цилиндр — с другой (все фигуры одинаковой высоты; радиусы оснований конуса и цилиндра равны радиусу шара).
В каждом сечении плоскостью, параллельной основаниям фигур, площадь сечения цилиндра равна сумме площадей сечений конуса и «южной» половины шара. Из этого равенства площадей следует равенство объёмов (так называемый принцип Кавальери).
Получается удивительная вещь: уравновесить две простые по форме гирьки — конус и цилиндр — удаётся с помощью более сложной — половины шара.