«Musica est exercitium arithmeticae occultum nescientis se numerare animi» (музыка — это тайное арифметическое упражнение души, которая вычисляет, сама того не зная). Прошло почти 300 лет с тех пор как Г. Лейбниц, один из основоположников математического анализа и старший современник И. С. Баха, написал эти великие слова в письме Х. Гольдбаху, однако они за это время не потеряли очарования и актуальности.
В наши дни математика даёт не только подходы в изучении существующих музыкальных произведений и передачи полученных знаний ученикам, но и новые творческие возможности, новые способы «конструирования» музыки.
Для хранения и передачи музыки используют нотную запись, которая содержит информацию о высоте нот, времени начала воспроизведения, длительности, громкости и музыкальных инструментах, на которых данная мелодия должна исполняться.
Какие преобразования этой последовательности приведут к мелодии, исполнение которой одновременно или последовательно с исходной было бы интересным и привлекательным?
Контрапункт. Простейшие математические операции, которые осваивает человек в первые годы своей жизни — арифметические операции сложения и вычитания. Простейшее преобразование мелодии, которому учат музыкантов — транспозиция: изменение высоты каждой ноты музыкальной последовательности на фиксированное (для данной транспозиции) число музыкальных единиц — полутонов. В случае нескольких голосов транспозиция одного относительно других называется вертикальным контрапунктом.
В труде Сергея Ивановича Танеева «Подвижной контрапункт строгого письма» (1906) впервые предъявляется математическая формула, описывающая контрапункт общего вида. Вот «модельный» пример вертикального контрапункта из этого учебника.
Изначально имеется два мелодических рисунка (голоса). Верхний голос остаётся на месте, а второй смещается на кварту вниз.
А вот пример из произведения И. С. Баха — фуги ми‐минор из первой части «Хорошо темперированного клавира» (1744). Она состоит из двух девятнадцатитактных частей и четырёхтактной коды (заключения). Вторая часть является почти точным вертикальным контрапунктом первой части, при этом смещены оба голоса. Сравним, например, два фрагмента из первой (такты 16‐17‐18) и второй (такты 31‐32‐33) частей.
Фрагмент первой части.
Фрагмент второй части.
Нетрудно видеть, что первый и второй голоса поменялись местами: высокий сместился вниз, а низкий перемещён наверх — т. е. к каждому голосу применён свой вертикальный контрапункт.
Как писал Альберт Швейцер, творчество Баха было долго недооценено, поскольку ноты его произведений воспринимались просто как формально красивый текст, не имеющий глубокого музыкального содержания. История показала, что формальные построения могут оказаться удивительно красивыми и на слух.
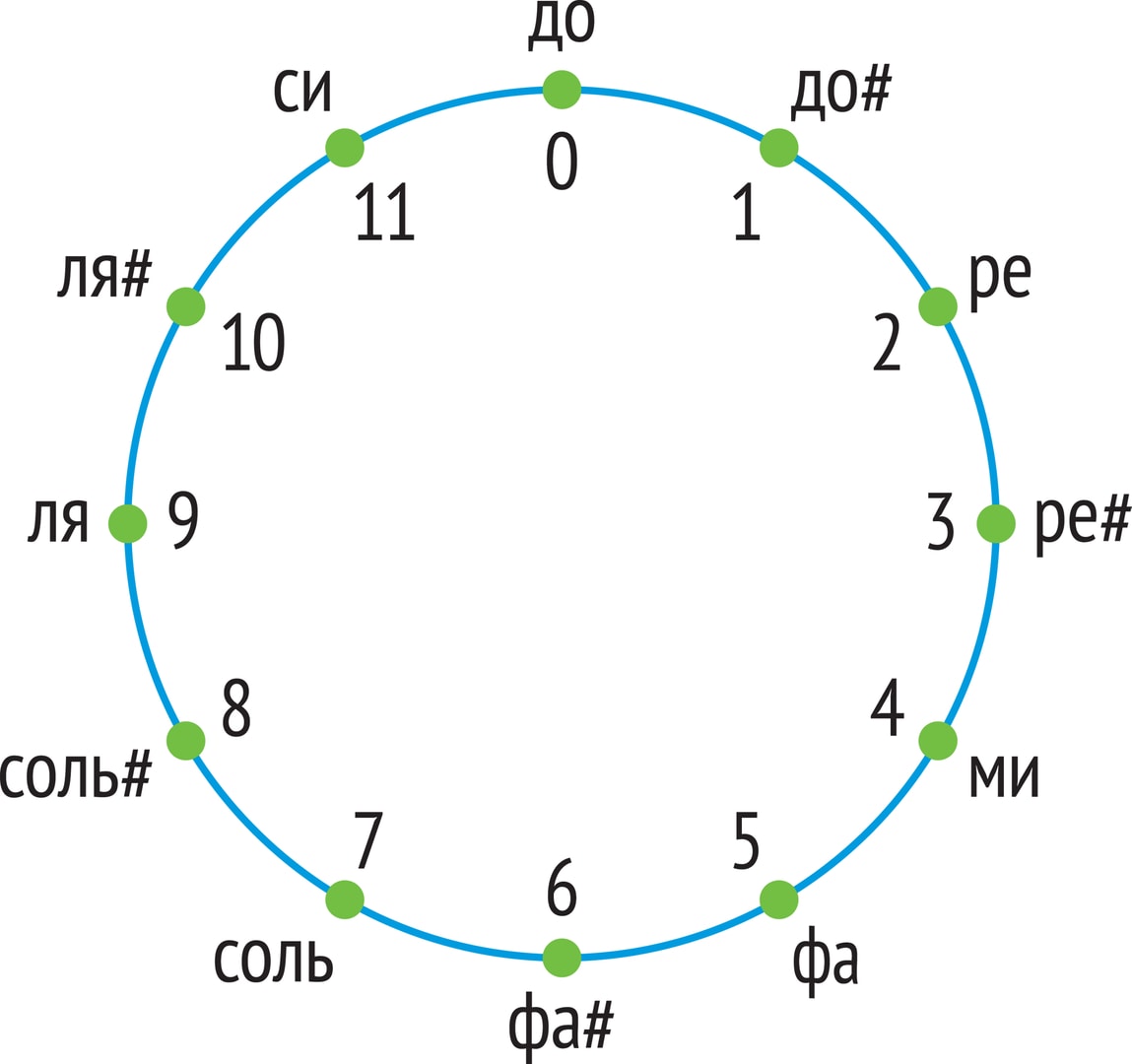
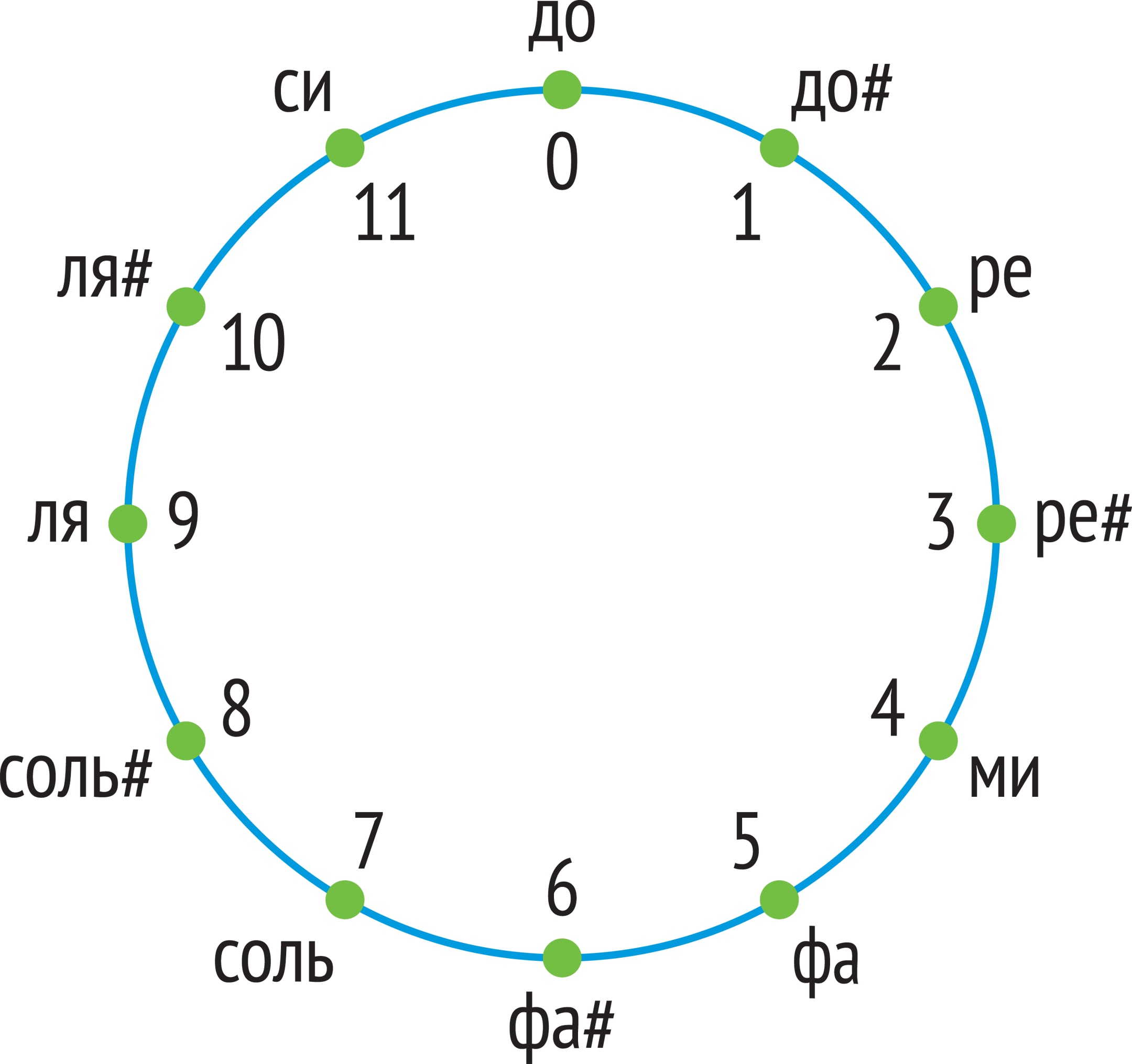
Арифметика по модулю n. Периодичность нот в гамме вызывает аналогии с периодическими множествами в математике, и это сопоставление порождает один из формально-математических методов сочинения музыки.
В мире целых чисел есть специальная, теоретико-числовая возможность расширения понятия равенства: два целых числа $a$ и $b$ называются сравнимыми («как бы равными») по модулю натурального числа $n$, если их разность $a-b$ делится на $n$, или, символически, $a\equiv b$ (mod $n$). Понятие сравнения ввёл великий математик К. Ф. Гаусс, он же предложил новую структуру — «арифметику по модулю $n$» (1801). В такой арифметике числа можно складывать, вычитать, умножать, иногда — даже делить.
Например, если модуль $n$ равен 12, то в этой арифметике будет ровно 12 различных чисел, их представителями удобно считать остатки при делении на 12 натуральных чисел: $ \{0, 1, …, 10, 11\} $. Примеры операций в этой арифметике: $8+5\equiv 1$, $8\cdot 5\equiv 4$.
Аналогия с хроматической гаммой: есть период, октава, состоящая из 12 нот. Прибавляя к ноте ре первой октавы 12 полутонов, получим ноту ре второй октавы, которая, как известно гармонирует с первой нотой, «сравнима» с ней!
Такой подход возник ещё в 1844 году. Его автор, французский музыковед Камиль Дюрут, обратил внимание на то, что при равномерно темперированном строе рояля множество интервалов разбивается на периоды из 12 ступеней. А это приводит к определению операций над музыкальными интервалами «по модулю 12».
Применение этих идей в сочинении музыки привело американского композитора Мильтона Бэббита даже к созданию целой музыкальной теории, так называемой «Set Theory» (1992), изложенной им в диссертации по математике!
Гармонический анализ. Простейшими гармониками являются тригонометрические функции 1, $\cos kx$, $\sin kx$ (для любого натурального числа $k$). Эти функции играют особую роль и в математике, и в акустике.
Следующие задачи принадлежат к числу основных в гармоническом анализе: представление заданной функции в виде суммы тригонометрического ряда, отыскание в виде суммы такого ряда функции, обладающей заданными свойствами (например, решения дифференциального уравнения, удовлетворяющего определённым начальным и краевым условиям).
В музыкальной акустике первая из перечисленных задач проявилась в предложенном Г. Л. Ф. Гельмгольцем методе исследования звука с помощью системы куполообразных резонаторов («резонаторы Гельмгольца»), позволяющих определить спектральный состав звука.
Вторая из упомянутых задач стала генератором возникновения аддитивного синтеза — одного из ярких направлений в музыке XX века. Заключается такой стиль в использовании искусственно созданных звуков, полученных суперпозицией большого числа простейших гармоник. Современный уровень компьютерной техники позволяет обойтись без механических приборов. В частности, французский композитор Жан‐Клод Риссе получил солидный набор электронных звуков, напоминающих звук колокола. На этом основывается его сочинение «Mutations» (1969).
Теория вероятностей. Применение вероятностных методов для написания музыки было предложено Янисом Ксенакисом. Ксенакис получил инженерное образование, работал с Ле Корбюзье, стал признанным архитектором. С другой стороны, всю жизнь занимался музыкой, стал не только известным композитором, но и музыковедом-теоретиком. Объединяло его работы, достижения и увлечения то, что всюду он применял или искал возможности применения математических методов.
Например, идея использования движения прямых — общая и для музыкальной пьесы 1954 года «Methastasis», в виде непрерывного глиссандо струнных, и для проекта павильона Phillips на всемирной выставке Expo‐58 в Брюсселе, поверхность крыши которого была получена непрерывным движением прямолинейных образующих.
Идея динамического развития музыкального сочинения согласно выбранной математической модели развивалось им после этого в течение многих лет. Модель определялась случайным процессом, который подбирался так, чтобы в заданные моменты времени получались намеченные автором спектр сигнала, распределение громкости по пространству и т. п.
Музыкальный манифест Ксенакиса — книга «Formalized Music» (1963), русский перевод — «Формализованная музыка» (2008). В частности, в книге разбираются возможности применения в сочинении и изучении музыки таких разделов математики как теория множеств, теория вероятностей, теория информации, теория игр.
Алгоритмика. Как известно, алгоритмом называется набор инструкций, описывающих порядок действий исполнителя для достижения поставленной цели за конечное число шагов. Если к входным данным применяется последовательно один и тот же алгоритм, то такой процесс называется итерационным. В математике самый употребительный вариант итерационного процесса — нахождение решения задачи методом последовательных приближений. Возможен и «исследовательский», поисковый вариант процесса, в котором отсутствует заранее намеченная цель.
В повседневной жизни итерационные процессы тоже не редкость, например, ежегодные начисления процентов на текущий банковский вклад увеличивают сумму для следующего процентного начисления (так называемый сложный процент).
Творческий процесс не может быть представлен в виде алгоритма. Тем не менее, особенно в современной музыке, возникновению у композитора идеи сочинения может предшествовать большая подготовительная работа, связанная с формальными вычислениями. Например, композитор задумал создать последовательность аккордов, обладающую определёнными свойствами. Такая последовательность может быть получена с помощью некоторого итерационного процесса. Конечно, полученная последовательность не будет музыкальным сочинением, но может рассматриваться как набор «кирпичей», из которых композитор будет создавать своё сочинение.
Целью французского композитора Тристана Мюрая в сочинении «Désintégrations» (1982) было получение последовательности аккордов с постепенно «расстраивающимся» соотношением между нотами. Начальный аккорд представлял из себя набор из 12 гармоник с рациональными соотношениями между частотами. В созданном композитором итерационном процессе, на каждом шаге аккорд изменялся совсем немного, но при этом у нот аккорда ухудшались соотношения частот, а длительность и время начала звучания — искажались.
Заключение. Мы рассмотрели лишь некоторые «музыкально-творческие» способности математики. Новая жизнь подобных подходов к написанию музыки связана с появлением мощной и доступной компьютерной техники. Начиная с середины 1990‐x годов появилось множество компьютерных программ для анализа и создания музыкальных произведений.
Например, есть секвенцерные программы, сохраняющие и расширяющие возможности классической нотации. В них сохраняется принцип последовательного считывания мелодии, а расширение состоит в том, что на параллельных дорожках могут быть написаны как ноты для обычных инструментов, так и специально подготовленные искусственные звуки. Подобные звуки создаются заранее с использованием гармонического анализа и других способов синтеза. Например, известной секвенцерной программой является программа LogicPro компании Apple.
Современные компьютерные инструменты, помогающие композитору, меняют и само понятие «музыка». Теперь музыкальное произведение может быть предъявлено не только перечислительно, например, в виде нотной записи или на барабане шарманки, но и в виде кода компьютерной программы, генерирующей это музыкальное произведение. Например, уже упоминавшееся произведение «Désintégrations» написано с помощью программы, включающей такие привычные для любого программиста объекты как циклы. Для композиторов, использующих математические идеи, разработаны системы программирования с удобным и красивым интерфейсом, являющиеся аналогом обычных языков программирования (LISP, FORTRAN, C). Подобная система может представить результат своей работы по выполнению кода программы в виде нотной записи, а может и выступить в роли исполнителя. Такой, например, является система OpenMusic, разработанная в парижском институте исследования музыкальной акустики.
Особый тип программ — интерактивные, т. е. такие, параметры которых могут меняться во время воспроизведения звука. Например, так работают программы, создающие видеоряд при исполнении музыкального произведения. Датчики, установленные на музыкальных инструментах, передают данные на компьютер, и установки программы меняются. К такому типу относится программа Max.
В заключение приведём слова Леонардо да Винчи, которые С. И. Танеев взял как эпиграф к упоминавшемуся труду «Подвижной контрапункт строгого письма»: «Nissuna humana investigatione si po dimandare vera scientia, s'essa non passa per le mattematiche dimostrationi» (ни одно человеческое исследование не может назваться истинной наукой, если оно не прошло через математические доказательства).
Танеев С. И. Подвижной контрапункт строгого письма. — Лейпциг, 1909.
Гельмгольц Г. Учение о слуховых ощущениях как физиологическая основа для теории музыки. — СПб., 1875.
Ксенакис Я. Формализованная музыка. — СПб.: Санкт-Петербургская гос. консерватория, 2008.
Теория современной композиции / Под ред. В. С. Ценовой. — М.: Музыка, 2005. — [Учебное пособие для студентов музыкальных вузов].
Puckette M. The theory and technique of electronic music. — World Scientific, 2007. — [Учебное пособие для студентов музыкального факультета Университета Калифорнии в Сан-Диего].