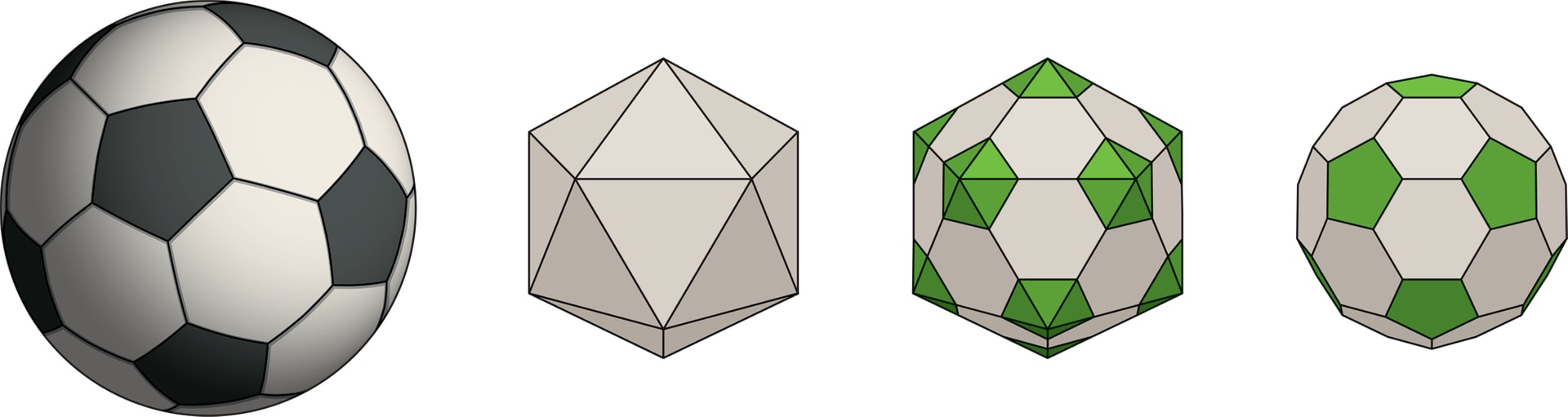
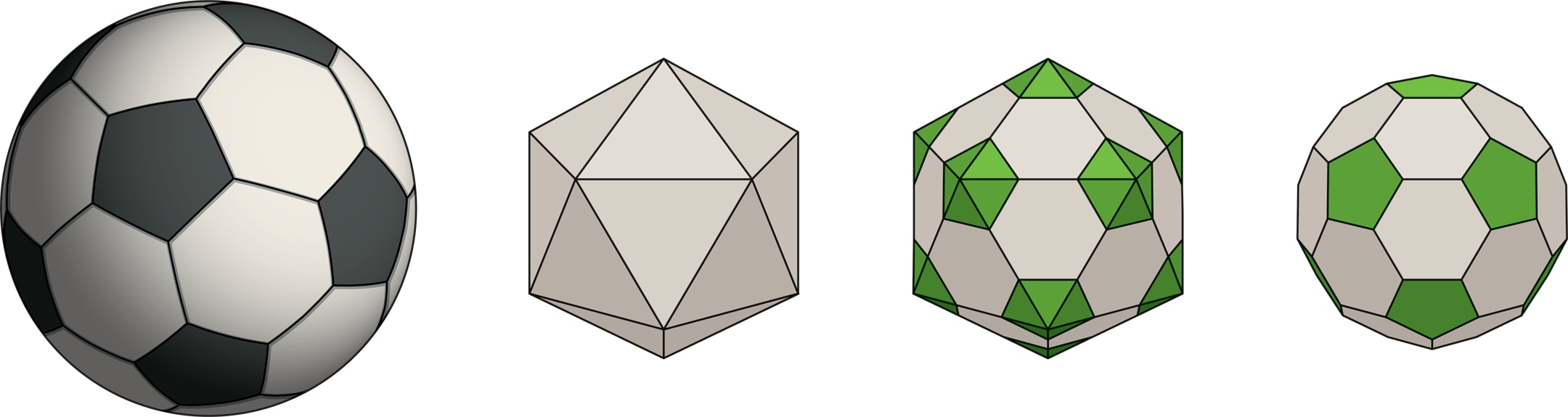
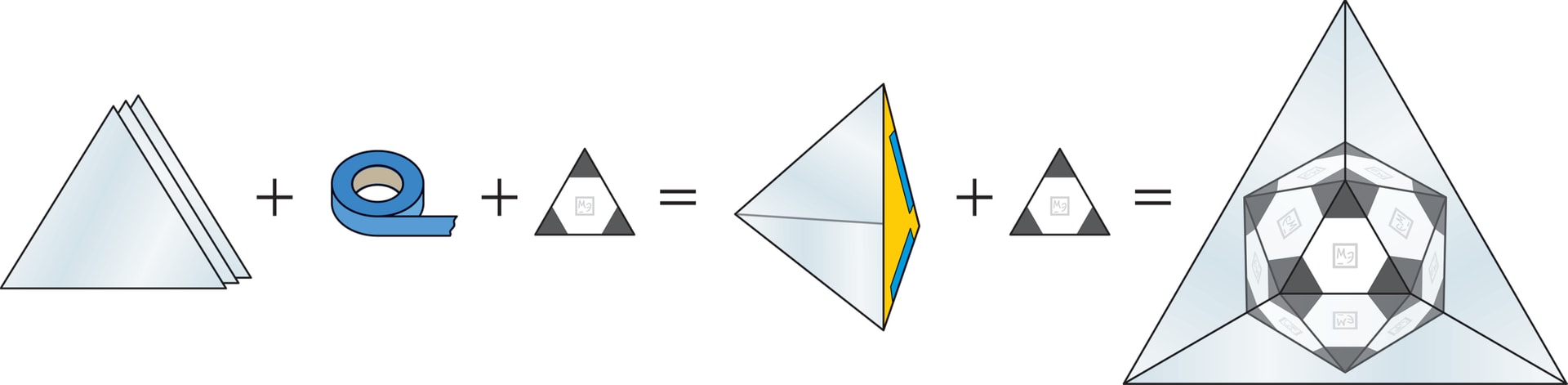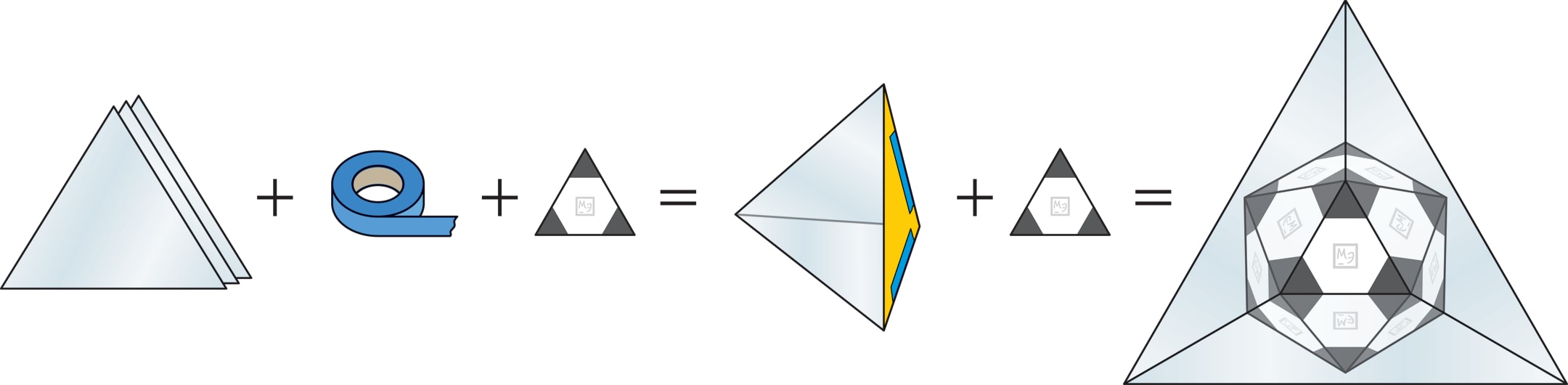Поверхность классического футбольного мяча состоит из слегка искривлённых 12 правильных пятиугольников чёрного цвета и 20 правильных белых шестиугольников. Модель мяча можно представить следующим образом.
Из 12 правильных пятиугольников и 20 правильных шестиугольников с равными сторонами можно сложить многогранник, называемый усечённым икосаэдром.
Икосаэдр — один из пяти правильных многогранников. Его название происходит от древнегреческих слов είκοσι — двадцать, έδρα — основание. У икосаэдра 12 вершин, 20 граней — правильных треугольников, 30 рёбер.
«Отрежем» (отсечём) вершины икосаэдра, отступив от вершин вдоль прямых, направленных в центр, на столько, чтобы оставшиеся части граней были правильными шестиугольниками. Срезы будут правильными пятиугольниками. Получившаяся фигура и есть усечённый икосаэдр.
Усечённый икосаэдр — один из полуправильных многогранников. Так называются многогранники, у которых все грани — правильные многоугольники нескольких разных типов (в отличие от правильных многогранников, все грани которых — одинаковые правильные многоугольники), а все вершины устроены «одинаково», т. е. многогранные углы при вершинах равны (совместимы).
При «наполнении воздухом» модели (усечённого икосаэдра) она принимает форму сферы, становится футбольным мячом. При этом вершины усечённого икосаэдра совпадут с «вершинами» мяча, рёбра перейдут в швы, а грани — в слегка искривлённые многоугольники на поверхности мяча. Таким образом получится мяч — центральная проекция усечённого икосаэдра на сферу.
Раздувание усечённого икосаэдра заставляет задуматься о степени близости к шару формы изначальной модели. Например, можно оценивать это сходство отношением радиусов концентрических сфер — описанной (проходящей через вершины; будущий мяч) и вписанной. Чем ближе это отношение к единице, тем совершеннее модель, тем ближе она к идеально круглому мячу.
А нельзя ли придумать модель мяча, состоящую из плоских кусков (панелей), но более совершенную, чем классическая? Можно было бы взять не усечённый икосаэдр, а многогранник с большим числом вершин, но это не устраняет принципиальный недостаток — выступающие над вписанной сферой «пирамидки» (вершины), мешающие модели стать сферой. К тому же процесс изготовления существенно усложняется.
Классический пятнистый мяч появился только в 1950 году. Он был официальным мячом на чемпионатах мира с 1970 до 2002 года. Затем наступило время экспериментов, а в 2014 году на чемпионате мира в Бразилии состоялась премьера нового официального мяча, получившего название «Бразука».
Модель «Бразуки» совершеннее классической и при этом «является кубом»! Как и куб, она собирается из шести одинаковых плоских панелей, на ней выделяются восемь особых точек (вершин), в каждой из которых сходится по три панели.
На границе каждой панели есть четыре угла по $120°$. В вершинах модели встречаются три угла, сумма их величин равна $360°$, поэтому поверхность мяча вокруг вершины будет уплощённой, выступающей пирамидки не будет.
Панели можно склеивать по линиям границ между углами, поскольку длины этих линий одинаковы. Выпуклые участки границ склеиваются с вогнутыми, а линии подобраны так, что в каждой точке склейки кривизна выпуклого участка больше кривизны вогнутого. Из‐за этого плоские панели при склеивании изгибаются, образуя в результате замкнутую выпуклую поверхность. Возможность такой склейки гарантирует теорема А. Д. Александрова, академика и автора школьного учебника по геометрии.
В модели классического мяча вся кривизна сосредоточена в конечном числе «выступающих» вершин. А в модели «Бразуки» она распределена более равномерно (по длинным рёбрам), и из‐за этого модель становится более близкой к сфере.
Официальный мяч чемпионата мира 2018 года в России назывался «Telstar 18». Его окраска напоминала мяч «Telstar» чемпионата 1970 года в Мексике, и по замыслу ФИФА название «Telstar 18» было данью уважения знаменитому мячу. А по конструкции «Telstar 18» похож на «Бразуку»: его образуют шесть одинаковых панелей, т. е. это мяч-куб. Отличие от мяча бразильского чемпионата — в форме панелей и, как следствие, в длине швов. У «Telstar 18» суммарная длина границ больше, значит, и кривизна больше «размазана» по поверхности мяча. Так что этот мяч с точки зрения математики — более круглый.
Соединение двух фактов, по отдельности встречавшихся в книге, позволит создать красивую модель, изготовление которой возможно и в домашних условиях. Первый факт — то, что классический футбольный мяч есть усечённый икосаэдр. Второй — понимание «работы» симметрий, порождённых отражениями в зеркалах (такие элементы теории групп встречались в статье «Калейдоскоп»).
Инструкция по изготовлению. Следует взять три одинаковых равнобедренных треугольника из зеркального пластика, в каждом основание равно 10 см, боковые стороны — по $9{,}5$ см. Сложите из них трёхгранный угол так, чтобы зеркальными были внутренние поверхности (грани можно скрепить клейкой лентой). Ещё одна деталь — правильный треугольник, не очень большой. Этот треугольник надо раскрасить в два цвета, например в чёрный и белый: около каждой вершины закрасить чёрным равносторонний треугольник, сторона которого втрое меньше стороны исходного, а оставшаяся часть (это правильный шестиугольник) будет белой.
Вложив раскрашенный треугольник в зеркальный трёхгранный угол, неожиданно увидим классический чёрно-белый футбольный мяч.
«Виртуальный» мяч будет виден целиком, если сторона треугольника-вкладыша будет не больше трети оснований равнобедренных зеркальных треугольников.
Магия появления футбольного мяча — в точно подобранных параметрах зеркального угла, связывающих его с икосаэдром: пропорции этого угла определяет правильная пирамида, вершина которой — центр икосаэдра, а основание — грань икосаэдра.
Точные пропорции: если $a$ — длина ребра икосаэдра (длина ребра основания в такой пирамиде), то длина бокового ребра пирамиды равна радиусу сферы, описанной около икосаэдра: $$ \large \frac{1}{4}\sqrt{2(5+\sqrt{5})} a ≈ 0{,}95a. $$