В организме человека как побочный результат происходящего в нём обмена веществ иногда образуются камни (например, в почках). Камни беспокоят, даже могут угрожать жизни, поэтому с ними приходится бороться.
Литотрипсия (от древнегреческого λίθος — камень) — один из методов дистанционного разрушения камней с помощью ударных волн. Принцип работы многих аппаратов дистанционного воздействия основан на геометрических свойствах эллипса.
Эллипс — геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, постоянна.
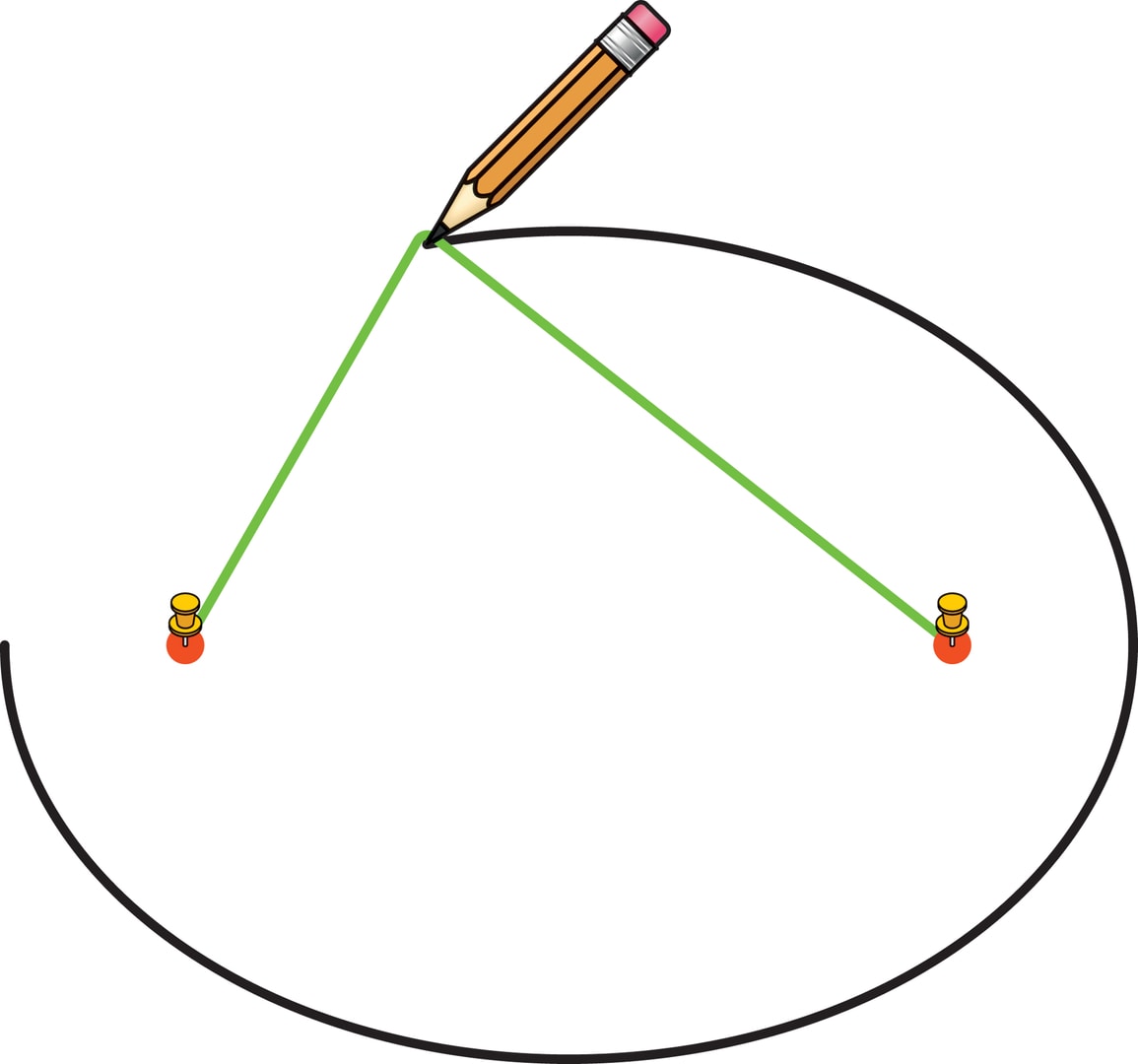
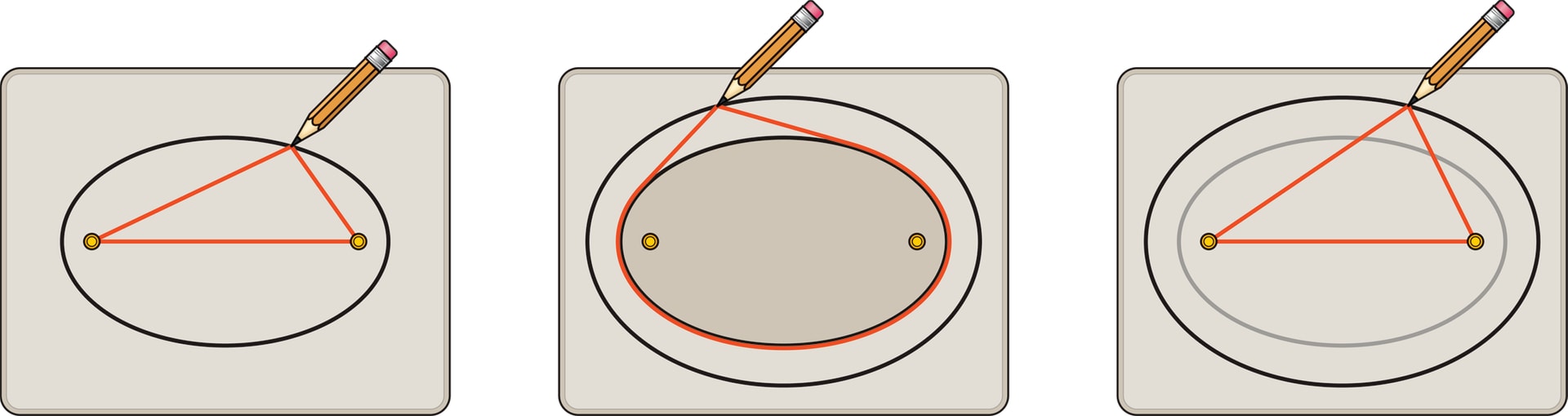
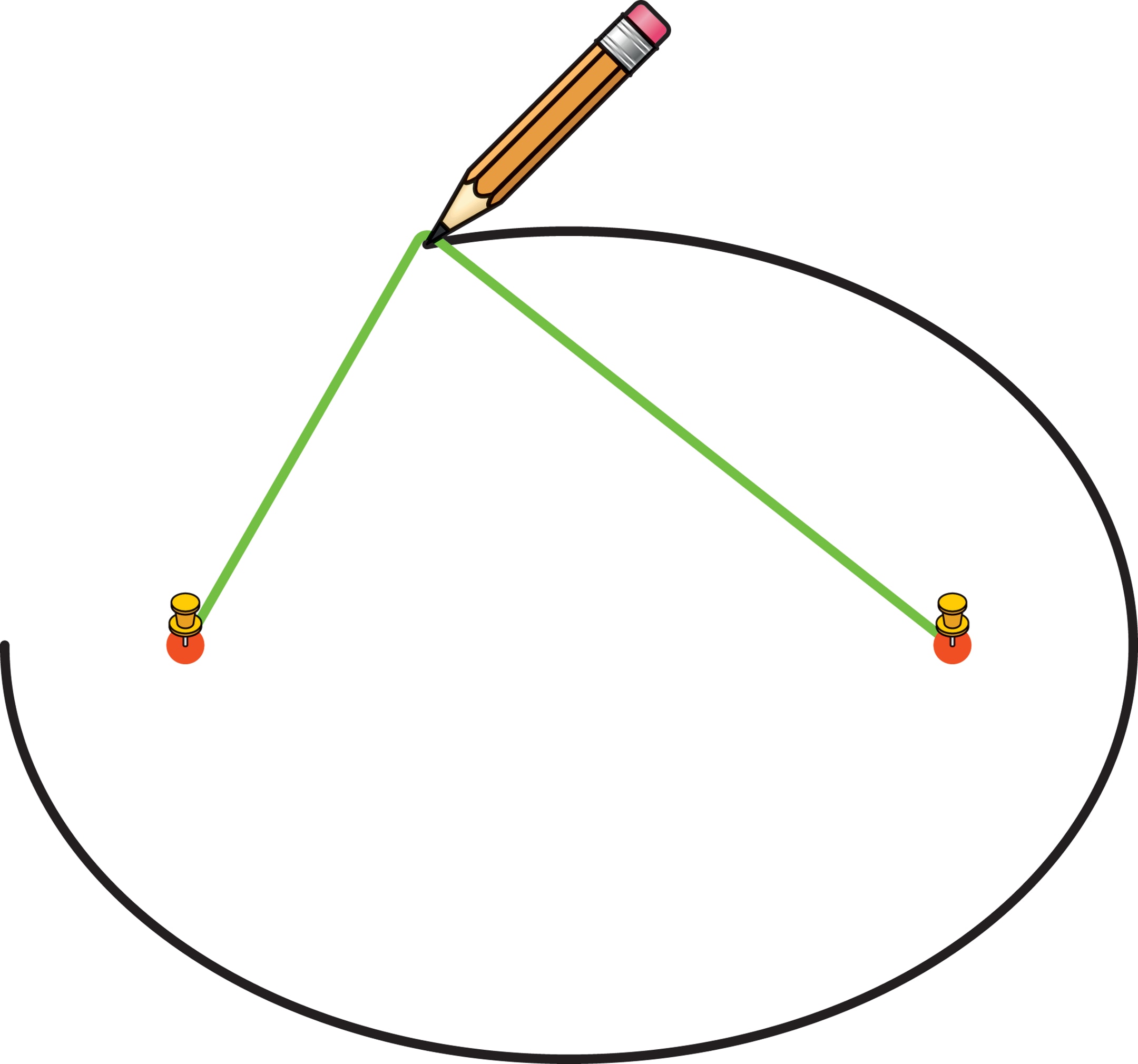
Это определение сразу приводит к способу построения эллипса. Привяжем концы нити к двум кнопкам, а их воткнём в лист бумаги. Если натянуть нить с помощью карандаша, поставить его на лист и, всё время сохраняя нить натянутой, провести линию, то получится дуга эллипса. Дело в том, что нить всё время будет иметь форму ломаной, состоящей из отрезков, соединяющих карандаш и кнопки-фокусы. Сумма длин этих отрезков постоянна и равна длине нити.
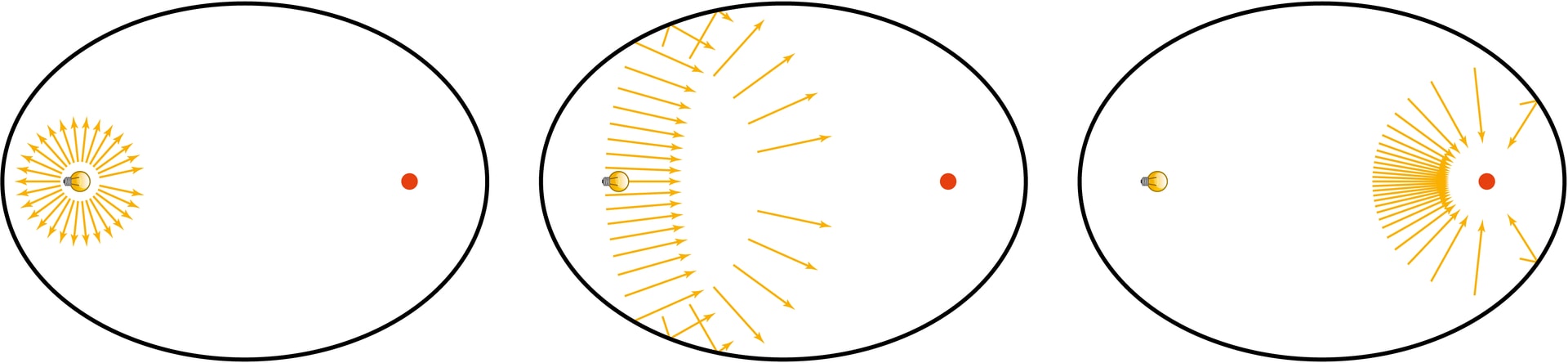
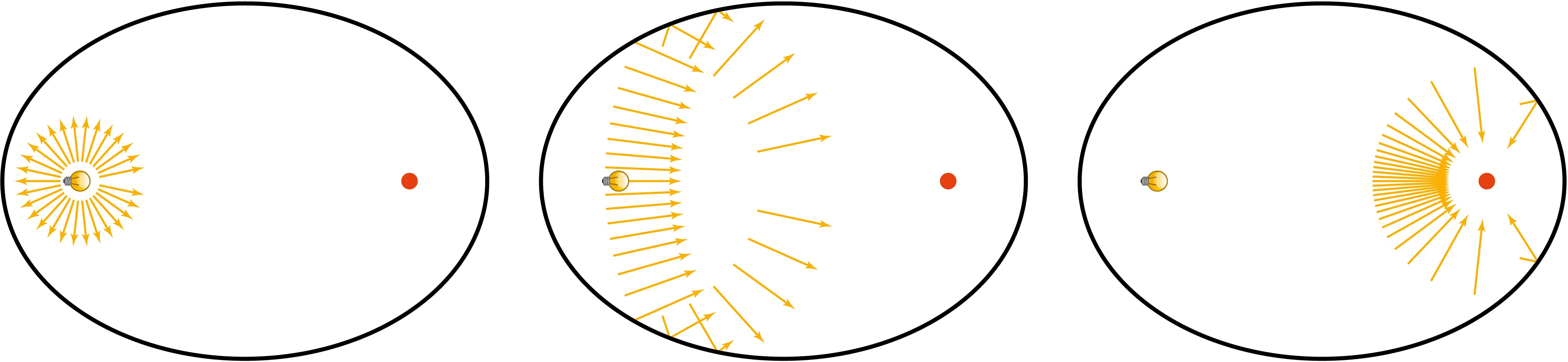
Как и парабола, эллипс обладает оптическим свойством. Если поместить точечный источник излучения («лампочку») в один из фокусов эллипса и включить его, то лучи, отразившись от эллипса, соберутся во втором фокусе. При этом все лучи придут во второй фокус одновременно, так как для каждого луча длина пройденного пути будет одна и та же (по определению эллипса).
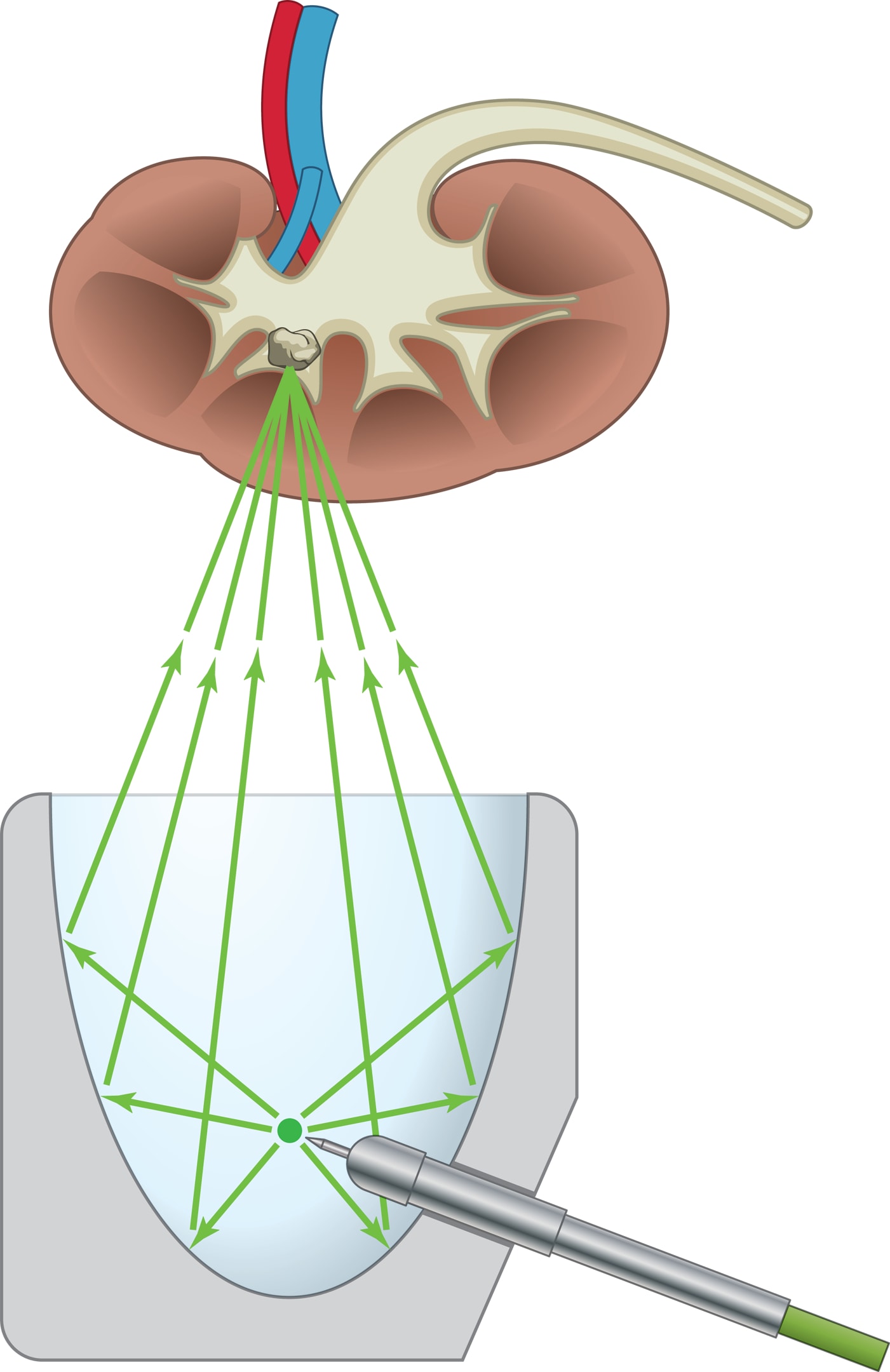
Именно это оптическое свойство эллипса используется в дистанционной литотрипсии.
При вращении эллипса вокруг прямой, проходящей через фокусы, получается эллипсоид вращения. В каждом сечении эллипсоида плоскостью, проходящей через ось вращения, получаются равные эллипсы с общими фокусами, поэтому эллипсоид тоже обладает оптическим свойством.
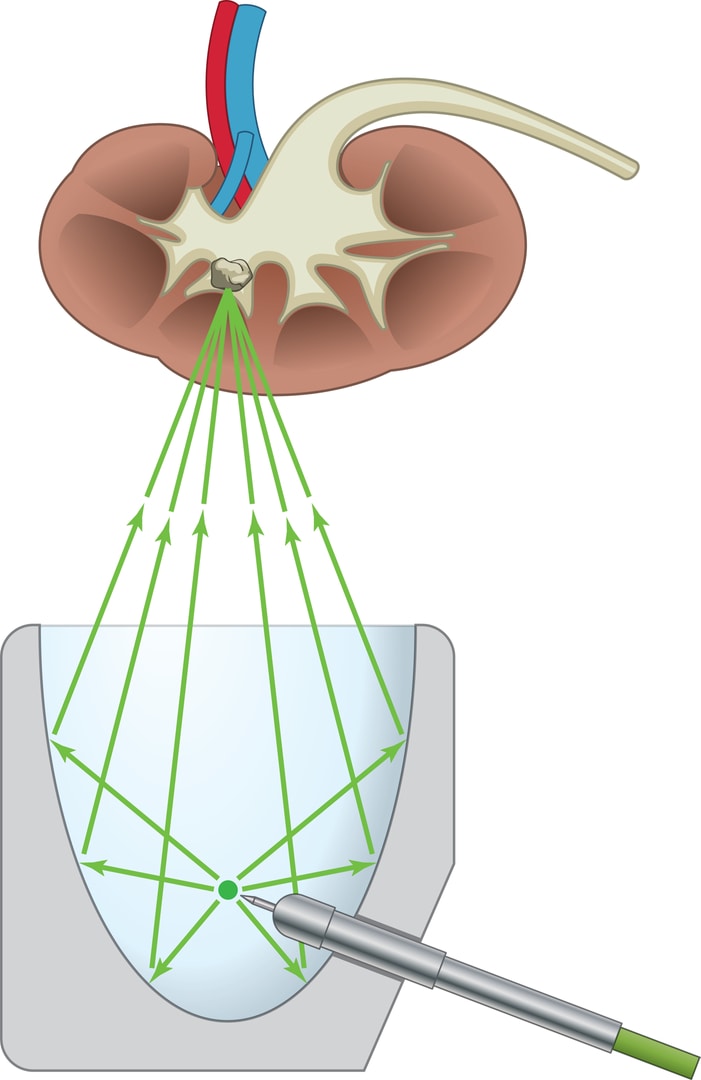
Отражатель аппарата дистанционной литотрипсии — часть эллипсоида, «чаша», примыкающая к одному из фокусов, в котором размещается источник излучения. Пациента помещают так, чтобы совместить положение второго фокуса и положение камня — мишени волновой атаки.
Конечно, излучение проходит и через ткани, окружающие камень, но только в фокусе одномоментно концентрируется вся энергия излучения, становясь и разрушающей, и целительной силой.
Приведём геометрическое объяснение оптического свойства эллипса.
Вышедший из фокуса луч, достигнув эллипса, отражается по закону «угол падения равен углу отражения» (отражение от кривой — это отражение от касательной к кривой в этой точке).
Если точку отражения луча соединить и со вторым фокусом, то получаются два отрезка нити из геометрического определения эллипса. На касательной к эллипсу, проведённой в точке отражения луча, все остальные точки лежат вне эллипса, поэтому для них сумма расстояний до фокусов будет больше.
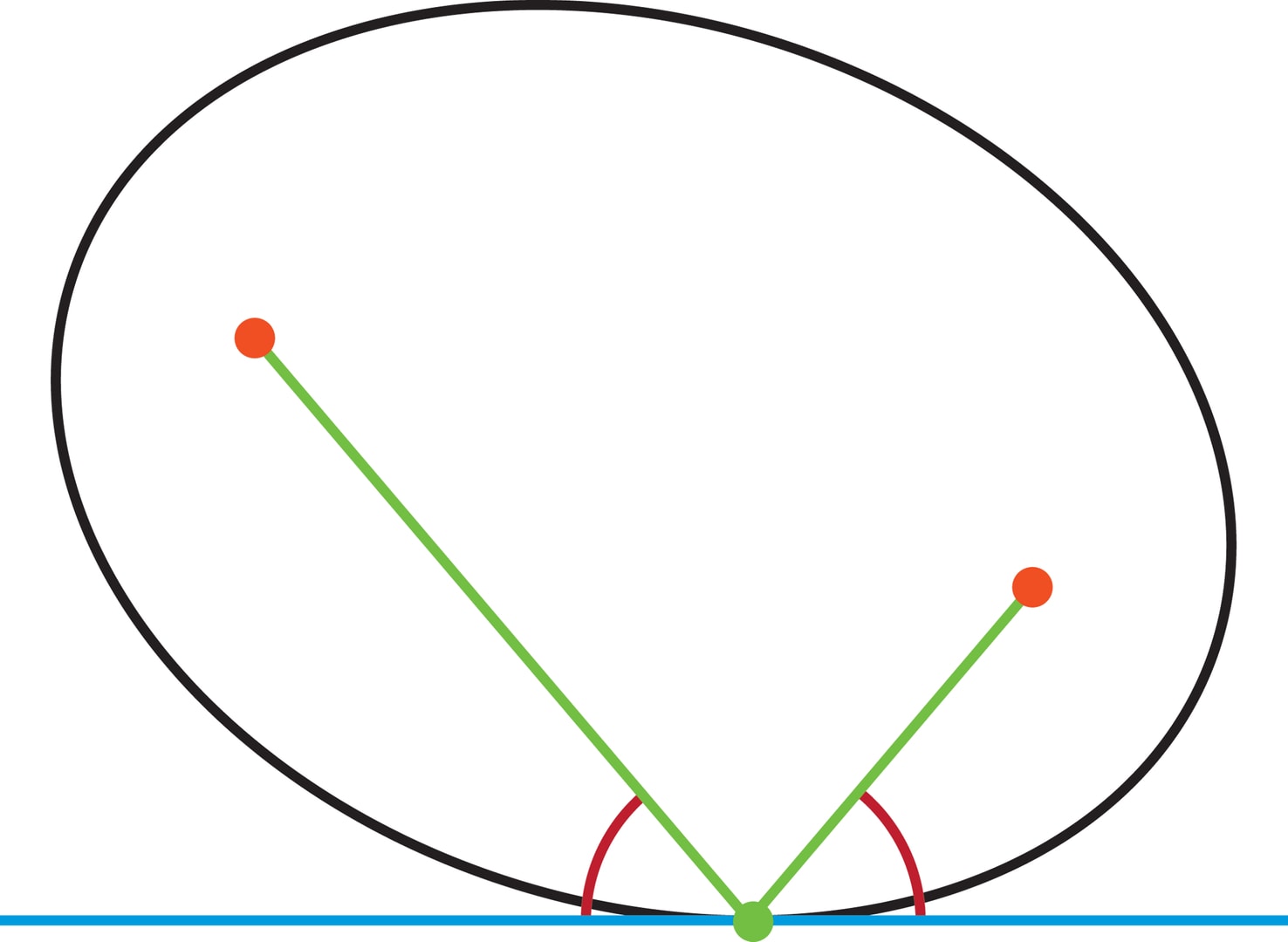
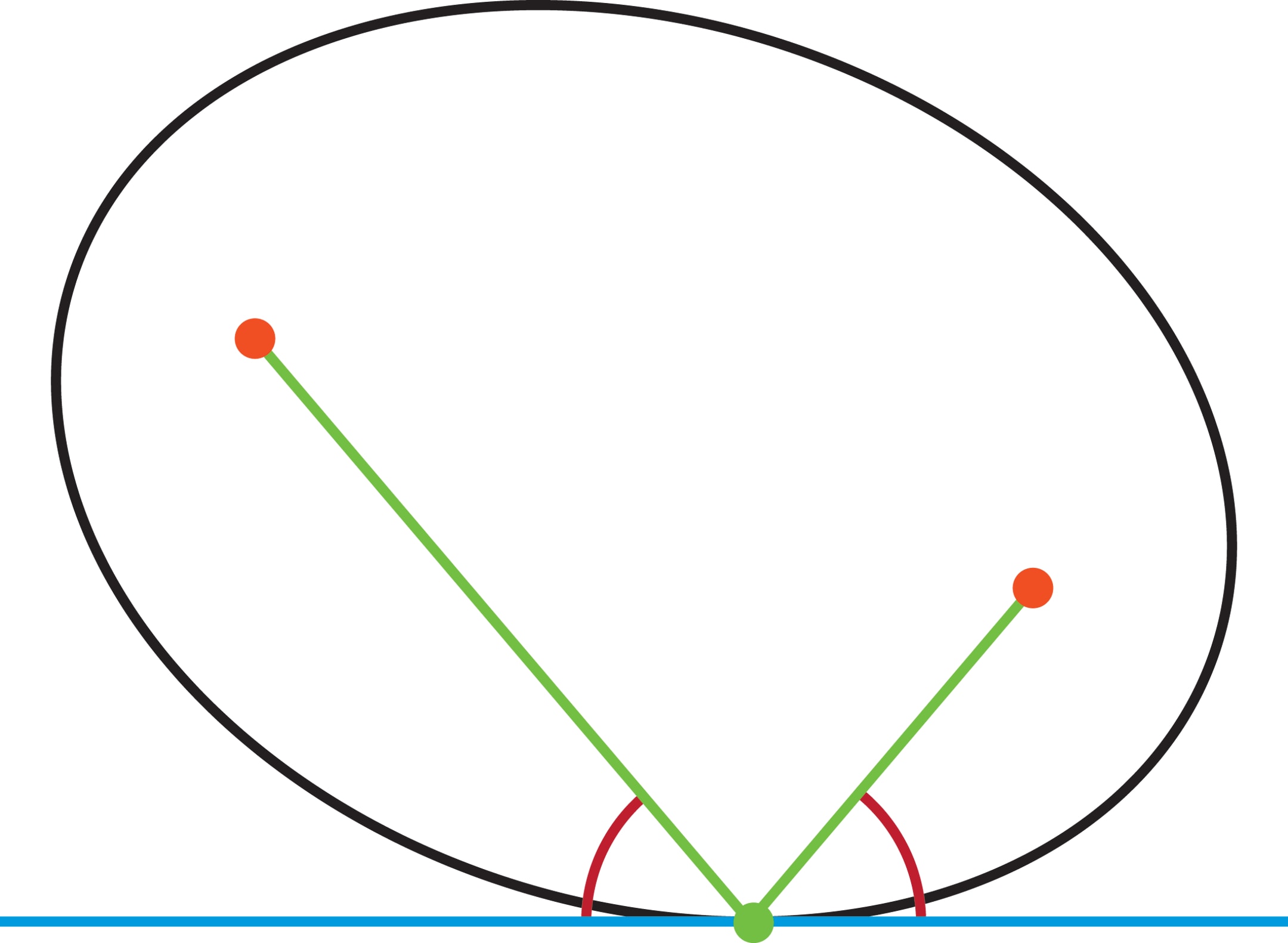
Воспользуемся теперь результатом фольклорной «задачи о Красной Шапочке», в которой внучка должна дойти от своего дома до реки (прямой), наполнить ведро и отнести его в дом бабушки. Кратчайший путь характеризуется тем, что отрезки, соединяющие дома с точкой «водозабора» на берегу, должны быть наклонены к прямой под одинаковыми углами.
В нашем случае дома — фокусы, река — касательная, кратчайший путь — отрезки нити, «рисующей» эллипс. Следовательно, эти отрезки образуют с касательной равные углы, а сама нить становится для луча «путеводной».
Построение эллипса с помощью нити открывает дорогу к построению софокусных эллипсов и «дарит» любопытные факты из жизни этих кривых.
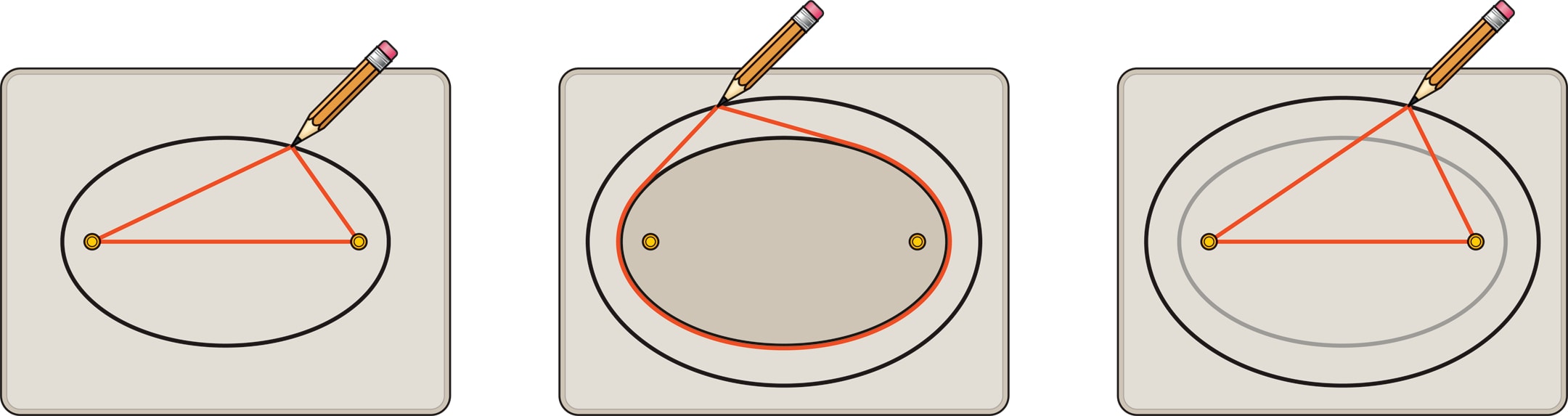
Взяв нить со связанными концами, охватывающую фокусы, и натянув её с помощью карандаша, нарисуем эллипс. Нити разной длины дадут целое семейство софокусных эллипсов. Но можно охватывать не отрезок, соединяющий фокусы, а один из уже полученных эллипсов.
Нарисовав эллипс, изготовим его «физическую» копию из достаточно толстого материала, а затем совместим копию с оригиналом. Возьмём нитяную петлю, которой можно охватить эллипс, и, оттянув её карандашом, проведём овальную линию. Оказывается, это тоже эллипс, причём софокусный исходному. Утверждение можно проверить экспериментально, подобрав длину петли, охватывающей фокусы.
Эту теорему в XIX веке доказал ирландец Чарльз Грейвс, епископ и математик. В книге Феликса Клейна «Высшая геометрия» один из параграфов называется «Построение из нитей Грейвса и Штауде».
Доказательство теоремы Грейвса можно прочитать в книге Клейна. Отметим, что оно не является элементарным, причина в том, что в каждый момент нить как линия состоит из двух отрезков, касательных к эллипсу, и дуги эллипса. Удивительно, но дуга эллипса — непростой объект, её длина выражается сложной формулой (используются так называемые эллиптические интегралы).
Эллипсограф — устройство для вычерчивания эллипсов — можно встретить уже в работах Леонардо да Винчи. Такие механизмы несложно изготовить и в домашних условиях.
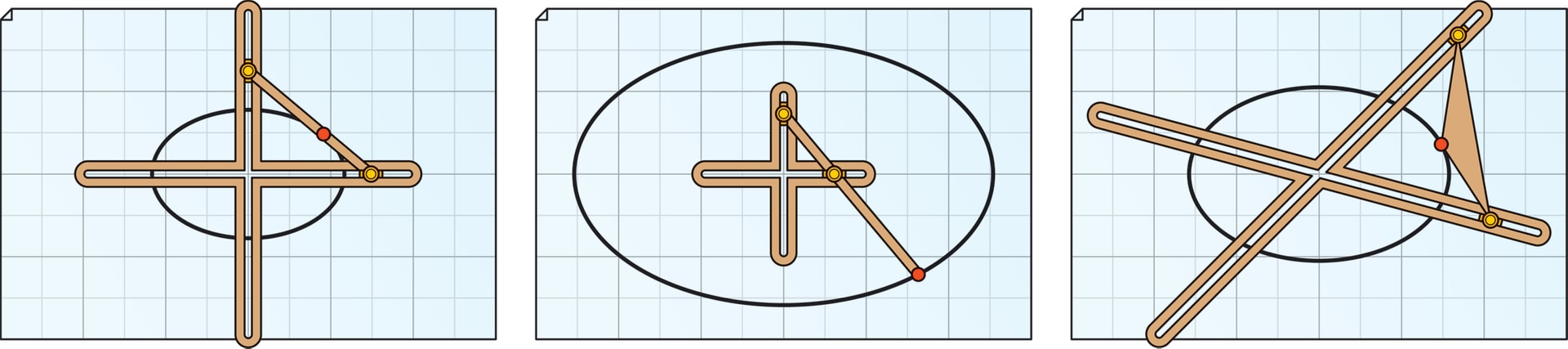
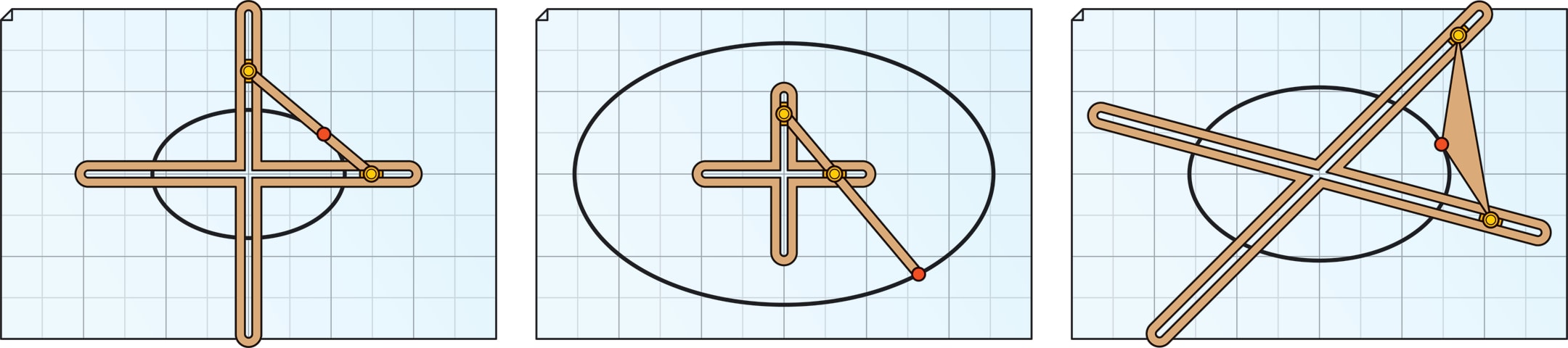
Простейшая идея: точка отрезка, концы которого скользят по двум перпендикулярным прямым, описывает эллипс. Модификация: точка выбирается на продолжении отрезка.
Более редкая идея. Две вершины треугольника скользят по двум пересекающимся прямым (не обязательно перпендикулярным) — траектория третьей вершины будет эллипсом.
О происхождении и значении термина «фокус», об эллипсе как огибающей семейства прямых и о том, как получить эллипс в виде муарового узора, см. комментарии к статье «Параболическая антенна». Про конические сечения см. комментарии к статье «Шуховские башни».
Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2‐е изд. — М.: Наука, 1978. — [Ко 2‐му изданию книга была значительно переработана и дополнена, с тех пор переиздавалась несколько раз].
Маркушевич А. И. Замечательные кривые. — М.—Л.: ГИТТЛ, 1952. — (Популярные лекции по математике; Вып. 4).
Эллипс