То, как человек воспринимает цвета, изучали и поэты, и естествоиспытатели, и математики (И. Гёте, Т. Юнг, Дж. Максвелл, Г. Гельмгольц, Г. Грассман и др.). В середине XIX века математик Г. Грассман, один из создателей теории векторных пространств, показал, что цветовое пространство (цветовые ощущения человека) можно рассматривать как «трёхмерное векторное» пространство.
Векторность означает, что вводятся правила сложения цветов и умножения на числа. Сложение — это смешение цветов, умножение на число — изменение интенсивности.
Трёхмерность означает, что, выбрав набор из трёх независимых цветов (т. е. таких, что ни один из них нельзя получить смешением двух других), мы сможем любой различимый глазом цвет получить как их комбинацию. Выбранные три цвета можно воспринимать как базис в цветовом пространстве, а любой цвет — как линейную комбинацию базисных векторов.
Например, из законов смешения цветов, установленных Грассманом, вытекает следующее. Пусть $\{A,B,C\}$ — некоторый базис в цветовом пространстве, тогда «колоритная» операция смешения цветов с координатами $(a_1;b_1;c_1)$ и $(a_2;b_2;c_2)$ сводится к сложению векторов — итоговый результат будет представлен вектором $(a_1+a_2;b_1+b_2;c_1+c_2)$.
Рассмотрим некоторые употребительные модели цветового пространства.
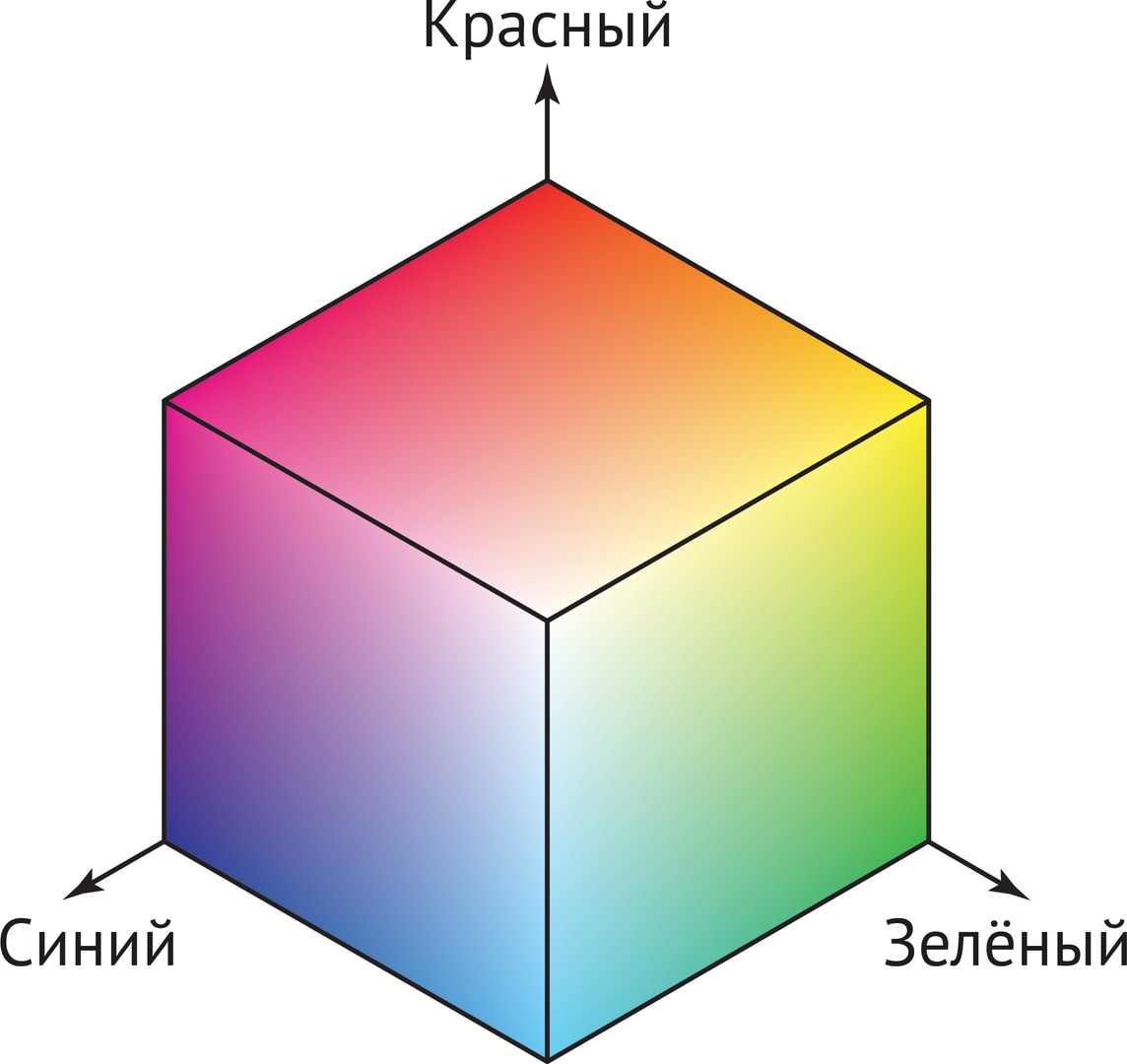
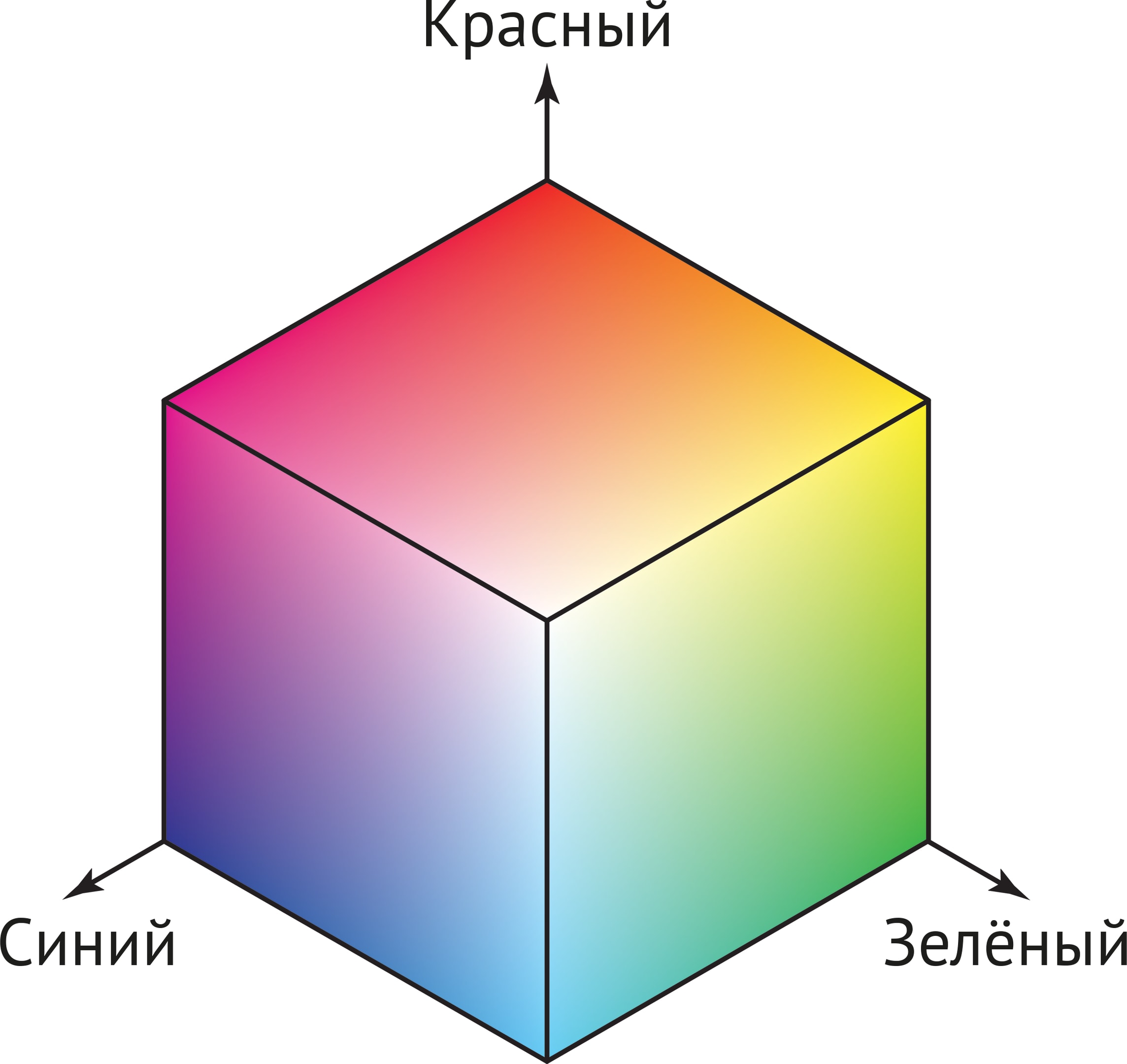
В мире компьютерных и планшетных экранов} — излучающих устройств, свет от которых попадает на сетчатку глаза, — для моделирования восприятия цветов человеком обычно используется модель RGB, предложенная в XIX веке физиком Дж. Максвеллом. В этой модели в качестве трёх базисных цветов выбраны: красный (Red), зелёный (Green) и синий (Blue). Эти цвета независимы — ни один из них нельзя получить как комбинацию двух других. С другой стороны, большую часть различимых глазом цветов можно получить как их комбинацию. Таким образом, набор R, G, B можно воспринимать как базис в соответствующем «цветовом» трёхмерном пространстве, которое удобно представлять в виде единичного куба. В этой модели координатные оси — базовые цвета R, G, B; начало координат совпадает с вершиной куба и символизирует чёрный цвет («отключены» все цвета, $\mbox{r}=\mbox{g}=\mbox{b}=0$). А противоположная вершина куба — «белая» (смешаны все три базисных цвета максимальной интенсивности, $\mbox{r}=\mbox{g}=\mbox{b}=1$).
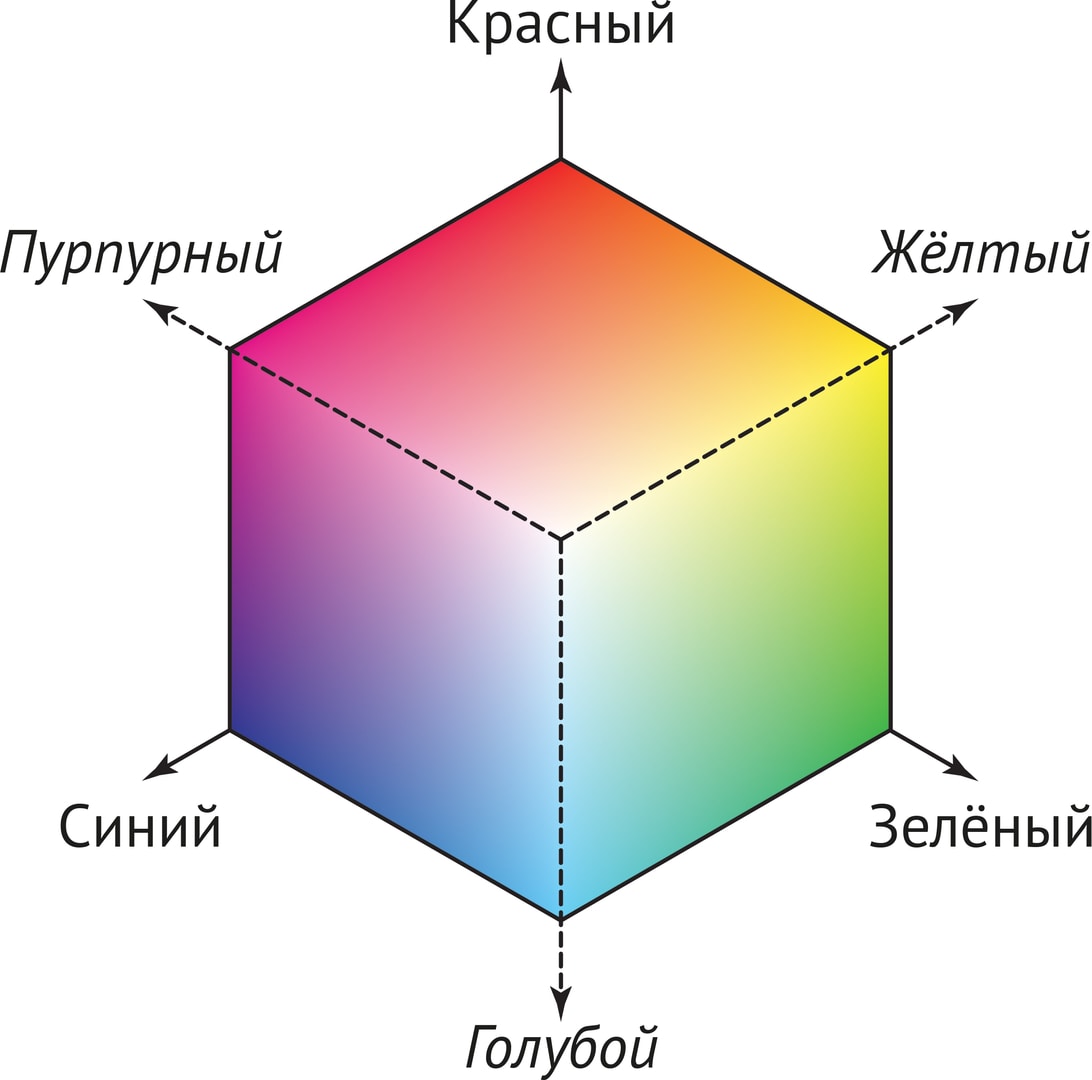
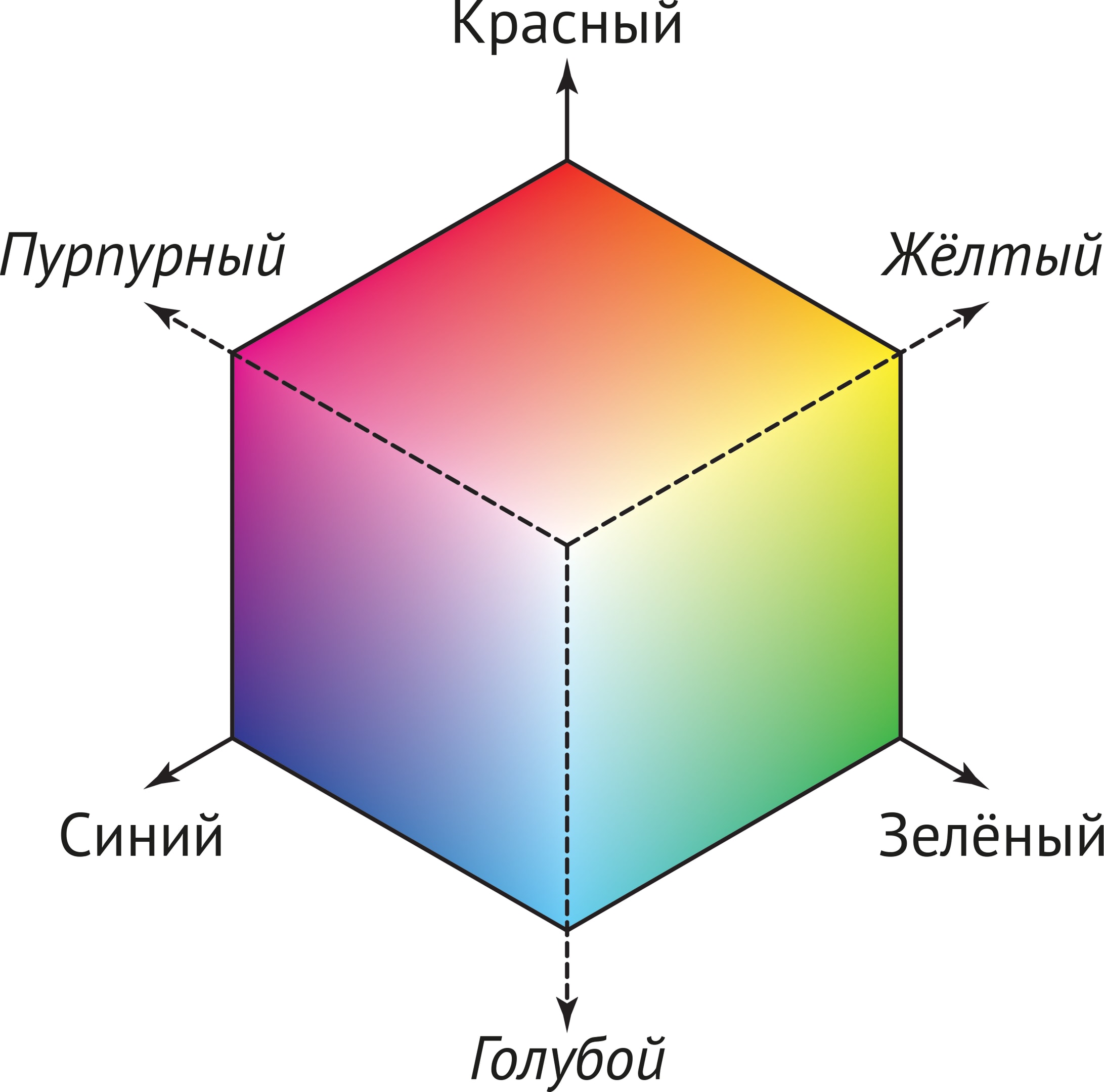
В цветной полиграфии, в том числе и при печати данной книги, основой является другой набор базисных цветов, CMY: голубой (Cyan), пурпурный (Magenta) и жёлтый (Yellow). В единичном «цветовом» кубе система координат, связанная с моделью CMY, следующая: начало координат — вершина куба, представляющая белый цвет, а координатные оси — базовые цвета C, M, Y.
Системы координат базисов RGB и CMY как бы смотрят друг на друга.
То, что в двух приведённых ситуациях (экраны и книги) используются разные модели цветового пространства, довольно естественно. Для экрана компьютера начальное (нулевое, невозмущённое) состояние характеризуется чёрным цветом. Соответственно, начало координат модели RGB — чёрный угол «цветового» куба. Для книги, бумаги первичное (начальное) состояние задаётся белым цветом (никакие краски на лист ещё не нанесены). Соответственно, начало координат модели CMY — белый угол куба.
Взаимное расположение осей, представляющих разные модели (RGB и CMY), определяется физическими соображениями и механизмом возникновения цветовых ощущений у человека. Так, при падении света окрашенный лист бумаги поглощает некоторые цвета, и в отражённом свете мы видим цвета, дополнительные к нанесённым на лист. Получается, что лист воспринимается зелёным, если он окрашен в цвета, дополнительные к зелёному.
Определение дополнительных цветов, которые надо наносить на бумагу, можно провести с помощью простых формул, связывающих координаты цвета (т. е. точки цветового куба) в системах RGB и CMY: цвета $(\mbox{r};\mbox{g};\mbox{b})$ и $(\mbox{c}; \mbox{m}; \mbox{y})$ совпадают, если $$ \mbox{c}=1-\mbox{r},\quad \mbox{m}=1-\mbox{g},\quad \mbox{y}=1-\mbox{b}. $$
Эти формулы дают ответ на вопрос: как подобрать краску $(\mbox{c}; \mbox{m}; \mbox{y})$, чтобы залитая ею область воспринималась как область цвета $(\mbox{r};\mbox{g};\mbox{b})$.
Например, чтобы область листа казалось красной, $(\mbox{r}; \mbox{g}; \mbox{b})=(1; 0; 0)$, её надо залить краской $(\mbox{c}; \mbox{m}; \mbox{y})=(0; 1; 1)$, т. е. смешать краски M и Y, не добавляя С.
Разумеется, приведённые формулы можно читать и «справа налево»: $$ \mbox{r}=1-\mbox{c},\quad \mbox{g}=1-\mbox{m},\quad \mbox{b}=1-\mbox{y}. $$
В этих формулах описано цветовое впечатление, которое сложится, если закрасить область краской $(\mbox{c};\mbox{m};\mbox{y})$.
Для получения чёрного цвета в модели CMY надо смешать три базисные краски максимальной интенсивности: $(\mbox{c}; \mbox{m}; \mbox{y})=(1; 1; 1)$. Однако полиграфически результат такой операции не очень хорош: есть технологические проблемы, да и при печати текста видно, говоря словами Ильфа и Петрова, что получается не «радикально-чёрный цвет». Поэтому к базису добавляют ещё один цвет (обозначаемый буквой K), обычно чёрный, предназначенный, в первую очередь, для печати текста. Такая модель называется CMYK. (И в этой статье в дальнейшем примем за K чёрный цвет.)
При четырёх компонентах CMYK теряется однозначность представления цветов. Например, и доля чёрного $(0; 0; 0; 0{,}2)$, и смешение трёх компонент $(0{,}2; 0{,}2; 0{,}2; 0)$ соответствуют одному и тому же серому цвету.
Типографские машины наносят краску мелкими точками, которые на каждой (по компонентам CMYK) печатной форме распределяются с переменной плотностью (сами краски по интенсивности одинаковые), что и приводит к меняющейся от области к области интенсивности цвета. Заметим, что при такой технике печати возникает проблема муара — «незапланированного» геометрического узора, возникающего из‐за регулярности, правильности решёток. Применяемое на практике решение этой проблемы — чисто геометрическое: муар будет не так заметен, если решётки форм повёрнуты относительно друг друга.
Для выделенной области у каждой печатной формы — своя цифровая инструкция, число от 0 до 1: 0 означает, что в область точки данного базисного цвета ставить не надо, 1 — точки ставятся с максимальной плотностью (полная заливка), а промежуточные значения от 0 до 1 определяют плотность равномерного распределения окрашенных точек в области (отношение площади закрашенной части области к полной). Например, лист розового цвета (как оттенка красного) закрашен редко расставленными точками красок M и Y.
Подчеркнём, что координаты цвета в указанных базисах дают возможность называть цвета не ограниченным набором слов, а точно, наборами чисел. По координатам можно вычислить и ещё одну важную для восприятия цвета характеристику — светлоту. Светлота показывает, насколько цвет «разбавлен белым», «близок» к нему. Базисные цвета модели RGB человек ощущает как цвета различной светлоты. Если принять светлоту чёрного за 0, а белого — за 1, то эмпирически установлено, что в базисе RGB светлота цвета $(1; 0; 0)$ равна $0{,}299$, цвета $(0; 1; 0)$ — $0{,}587$, цвета $(0; 0; 1)$ — $0{,}114$. Векторность цветового пространства — возможность умножать на числа и складывать — позволяет записать формулу для светлоты цвета $(\mbox{r}; \mbox{g}; \mbox{b})$, «арифметически» описывающую человеческие ощущения: $$ \mbox{L}=0{,}299\mbox{r}+0{,}587 \mbox{g} +0{,}114 \mbox{b}. $$
Заметим, что значения числовых коэффициентов в этой формуле согласуются с тем, что три базисных цвета максимальной интенсивности $\mbox{r}=\mbox{g}=\mbox{b}=1$ дают белый цвет.
В цветовом кубе уравнение $\mbox{L}=\mbox{const}$ задаёт плоскость, все точки которой, при выполнении стандартной для графического редактора операции перевода в серую шкалу (Grayscale), переходят в одну точку — точку пересечения этой плоскости с диагональю «чёрный—белый». Таким образом, цветовой куб расслаивается на плоскости одинаковой светлоты.
Базисные цвета модели CMY человеком также воспринимаются как цвета различной светлоты (на рисунке представлены горизонтальными полосками). Формулы, связывающие координаты цвета в базисах RGB и CMY, дают аналогичную формулу для светлоты при разложении по второму базису.
Светлоту читатель может представлять как величину, обратно пропорциональную количеству тонера, расходуемого чёрно-белым копировальным устройством при передаче некоторой площади данного цвета. На рисунке левая вертикальная полоса в системе CMY имеет координаты $(0; 0{,}5; 1)$, правая — $(0{,}38; 0{,}5; 0)$. Значения светлоты $\mbox{L}$ для обеих полос совпадают, и их копии, сделанные на чёрно-белом копире, отличаться не будут.
Модели RGB и CMYK — канонические. Конечно, есть и другие модели, например, у дизайнеров популярны системы, в которых светлота становится одной из базисных координат (Lab, HSB). Ситуацию можно сравнить с описанием объектов трёхмерного пространства — можно использовать декартовы координаты (RGB, CMY), а можно — сферические (Lab, HSB).
На каждую из четырёх одноцветных печатных форм краска наносится по узлам одинаковых решёток, чаще — треугольных. Если бы решётки были совершенно одинаково расположены, то и печать была бы совершенной. Но небольшие смещения, в частности повороты, на практике неизбежны.
Именно регулярность, правильность решёток приводит к появлению муара — постороннего геометрического узора. Причина — поворот матриц друг относительно друга. Парадокс в том, что самый сильный муар наблюдается при малых угловых смещениях, а при значительных — муаровый узор настолько мелкий, что незаметен.
Если угол поворота двух решёток меньше $3°$, то последствия фатальны. Динамику изменения муара вплоть до исчезновения можно оценить, сравнивая результаты при повороте одной из двух форм на 5, 10, 20 и 30 градусов.
Предварительный поворот самих решёток на формах на достаточно большой угол справляется с заметным муаром. Но периодичность решёток вносит ограничения на величину этого угла: например, треугольная решётка при повороте на $60°$ переходит в себя. В этом случае при четырёхкрасочной печати — четырьмя формами — угол поворота не может превышать $15°$.