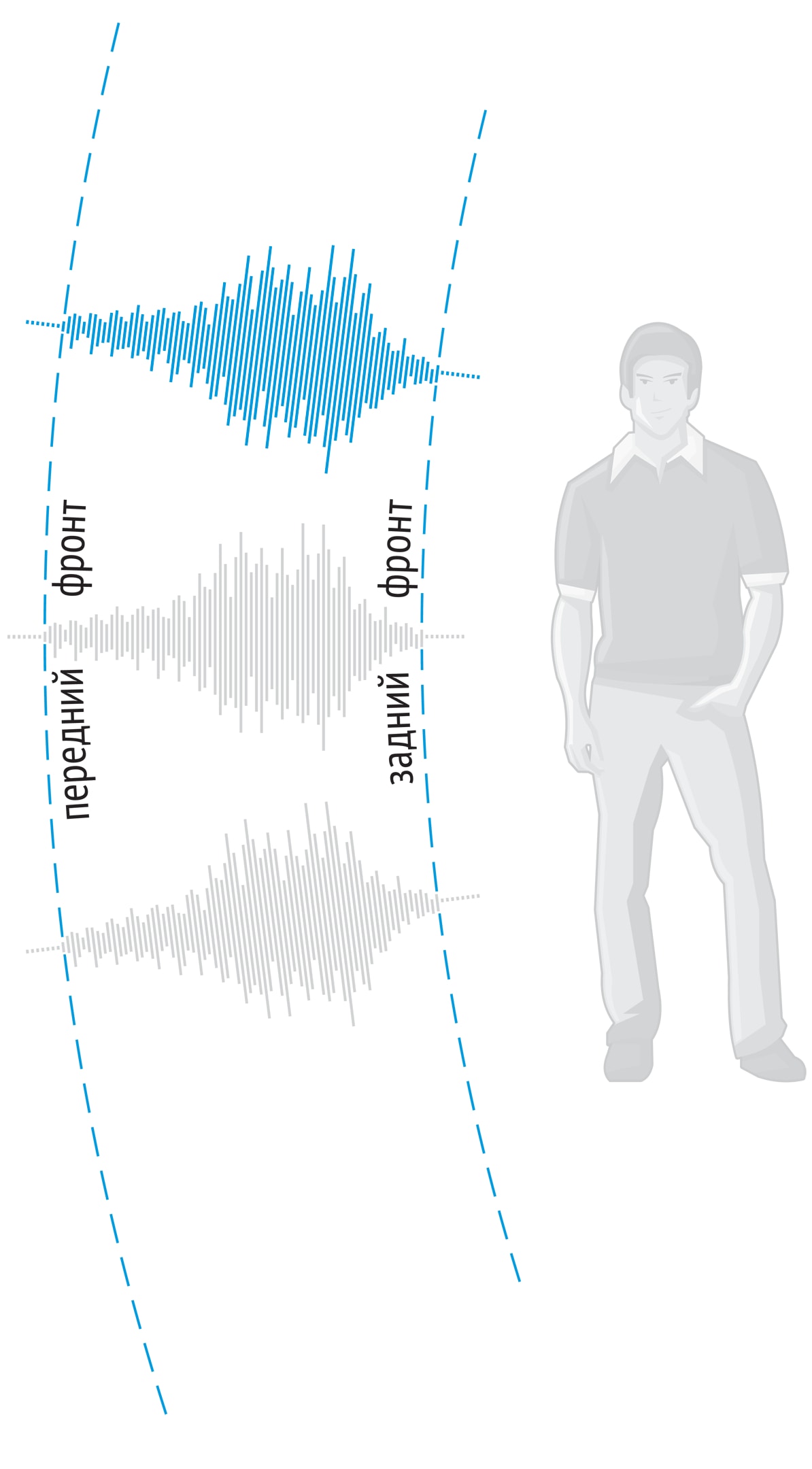
Традиция передачи знаний и эмоций в устной речи — одна из основ человеческой культуры. Оказывается, нам просто повезло с пространством, в котором звуковые волны распространяются так, что мы можем слышать то, что говорят другие.
В конце XVII века выдающийся голландский учёный Христиан Гюйгенс написал «Трактат о свете. В котором объяснены причины того, что с ним происходит при отражении и преломлении». В отличие от своего великого предшественника Рене Декарта, «полагавшего, что переход света совершается мгновенно» (цитата из упомянутого «Трактата»), Гюйгенс считал скорость света конечной. Это допущение позволило Гюйгенсу рассматривать с единой точки зрения вопросы распространения света и звука. Объединяющим стал термин «волна»: «Поскольку вместе с тем свет употребляет для своего прохождения некоторое время — вопрос, который мы сейчас рассмотрим, — из этого следует, что движение, сообщённое веществу, постепенно и, следовательно, распространяется так же, как и при звуке, сферическими поверхностями и волнами: я называю эти поверхности волнами по сходству с волнами, которые можно наблюдать на воде, в которую брошен камень…». В «Трактате» Гюйгенс привёл геометрическое описание того, как распространяется фронт волны — граница в пространстве, до которой дошла волна.
В XIX веке математики получили формулы, выражающие решения уравнений, описывающих положение звуковой волны в пространстве, при условии, что известно её состояние в начальный момент времени.
Из этих формул следовало, что помимо наличия переднего фронта волны, описываемого упомянутым принципом Гюйгенса, особенностью звуковых волн в трёхмерном пространстве является наличие заднего фронта. Возникнув в одной точке пространства, звук доходит до другой части пространства, а после покидает её и распространяется далее. Иначе говоря, моментальный источник волны остаётся моментальным при улавливании его в другой точке пространства. Данный эффект Адамар назвал принципом Гюйгенса в узком смысле.
Рассмотрим принцип Гюйгенса немного подробнее. Если в некоторой точке пространства есть мгновенный источник звука, то за время $t$ звук может распространиться в шаре с центром в этой точке и радиуса $ct$, где $c$ — скорость звука. Принцип Гюйгенса в узком смысле утверждает, что в действительности в момент времени $t$ звук распространится на сферу — границу этого шара, но он не будет слышен внутри шара.
Именно это свойство — наличие заднего фронта звуковой волны в трёхмерном пространстве — позволяет нам слышать друг друга. Если бы заднего фронта не было, то мы бы слышали одновременно все возможные звуки, дошедшие до нашего положения в пространстве, и они бы накладывались друг на друга. Отметим, что это свойство выполняется и для электромагнитных волн, включая световые.
Выполнение принципа Гюйгенса в узком смысле — явление редкое, зависит и от типа волнового процесса, и от свойств пространства (размерность, однородность). Так, на плоскости принцип перестаёт действовать даже для волнового уравнения, а в трёхмерном пространстве не выполняется для звуковых волн, распространяющихся в неоднородной среде.
Наглядный пример отсутствия заднего фронта — волны на поверхности воды: мгновенный источник фиксируется в другой точке поверхности на протяжении длительного времени. Можно наблюдать это явление, «бросая в воду камешки». Брошенный камень создаёт много расходящихся кругов, которые являются волной на поверхности воды. И эта волна, дойдя в другую точку поверхности воды, ещё долго там наблюдается. Лишь постепенно вода вновь успокаивается.
Доказано, что аналоги звуковых волн удовлетворяют принципу Гюйгенса в узком смысле только в нечётномерных пространствах размерности три и выше. Адамар сформулировал проблему, до сих пор остающуюся нерешённой: найти все дифференциальные уравнения, описывающие волновые процессы, для которых выполняется принцип Гюйгенса в узком смысле. Замечательно, что некоторые примеры таких уравнений в пространствах высоких размерностей можно получить с помощью правильных многогранников.
Гюйгенс Х. Трактат о свете. — М.—Л.: ОНТИ, 1935.
Веселовский И. Н. Христиан Гюйгенс. — М.: Учпедгиз, 1959.
Соловьёв Ю. Христиан Гюйгенс
Брэгг У. Мир света. Мир звука. — М.: Наука, 1967.
Берест Ю. Ю., Веселов А. П. Принцип Гюйгенса и интегрируемость