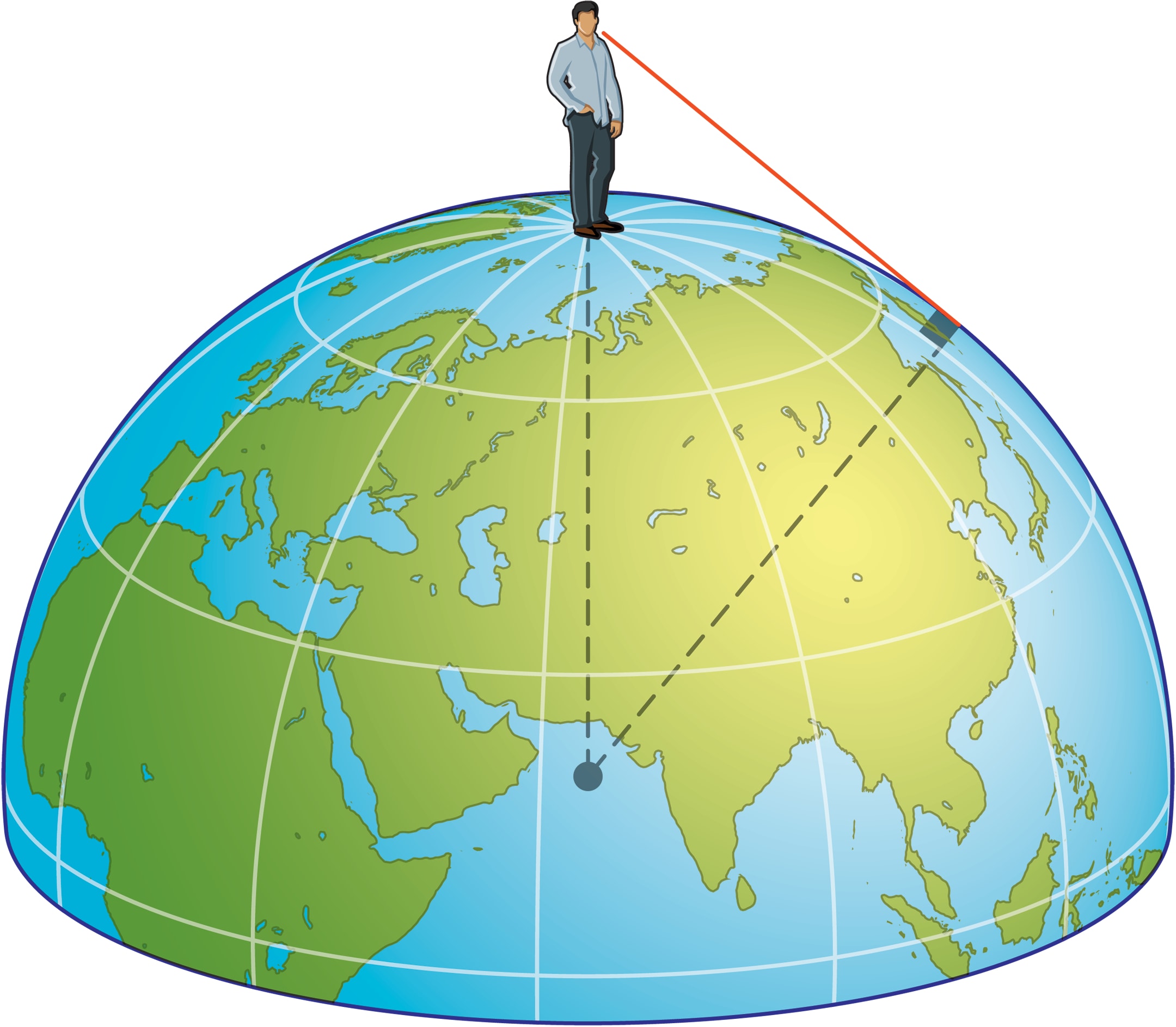
Какова дальность до линии горизонта для наблюдателя, стоящего на земле? Ответ — приближённое расстояние до горизонта — можно найти с помощью теоремы Пифагора.
Для проведения приближённых расчётов сделаем допущение, что Земля имеет форму шара. Тогда стоящий вертикально человек будет продолжением земного радиуса, а линия взгляда, направленного на горизонт, — касательной к сфере (поверхности Земли). Так как касательная перпендикулярна радиусу, проведённому в точку касания, то треугольник (центр Земли) —(точка касания) —(глаз наблюдателя) является прямоугольным.
Две стороны в нём известны. Длина одного из катетов (стороны, прилегающей к прямому углу) равна радиусу Земли $R$, а длина гипотенузы (стороны, лежащей против прямого угла) равна $R+h$, где $h$ — расстояние от земли до глаз наблюдателя.
По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы. Значит, расстояние до горизонта равно $$ d=\sqrt{(R+h)^2-R^2} = \sqrt{(R^2+2Rh+h^2)-R^2} =\sqrt{2Rh+h^2}. $$
Величина $h^2$ очень мала по сравнению со слагаемым $2Rh$, поэтому верно приближённое равенство $$ d≈ \sqrt{2Rh}. $$
Известно, что $R≈ 6400$ км, или $R≈ 64\cdot10^5$ м. Будем считать, что $h≈ 1{,}6$ м. Тогда $$ d≈\sqrt{2\cdot64\cdot10^5\cdot 1{,}6}=8\cdot 10^3 \cdot \sqrt{0{,}32}. $$
Используя приближённое значение $\sqrt{0{,}32}≈ 0{,}566$, находим $$ d≈ 8\cdot10^3 \cdot 0{,}566=4528. $$
Полученный ответ — в метрах. Если перевести найденное приближённое расстояние от наблюдателя до горизонта в километры, то получим $d≈ 4,5$ км.
Как связано расстояние до горизонта с изменением высоты точки наблюдения? Формула $d≈ \sqrt{2Rh}$ даёт ответ: чтобы увеличить расстояние $d$ вдвое, высоту $h$ надо увеличить в четыре раза!
В формуле $ d≈ \sqrt{2Rh} $ нам пришлось извлекать квадратный корень. Конечно, читатель может взять смартфон со встроенным калькулятором, но, во‐первых, полезно задуматься, а как же решает эту задачу калькулятор, а во‐вторых, стоит ощутить умственную свободу, независимость от «всезнающего» гаджета.
Существует алгоритм, сводящий извлечение корня к более простым операциями — сложению, умножению и делению чисел. Для извлечения корня из числа $a>0$ рассмотрим последовательность $$ x_{n+1}=\frac12 {\left(x_n+\frac{a}{x_n}\right)}, $$
где $n=0, 1, 2, …$, а в качестве $x_0$ можно взять любое положительное число. Последовательность $x_0$, $x_1$, $x_2$, … очень быстро сходится к $\sqrt{a}$: точность приближения возрастает вдвое после каждого шага.
Например, при вычислении $\sqrt{0{,}32}$ можно взять $x_0=0{,}5$. Тогда $$ x_1 =\frac12 {\left(0{,}5+\frac{0{,}32}{0{,}5}\right)}=0{,}57, $$ $$ x_2 =\frac12 {\left(0{,}57+\frac{0{,}32}{0{,}57}\right)}≈ 0{,}5657. $$
Уже на втором шаге мы получили ответ, верный в третьем знаке после запятой $ ( \sqrt{0{,}32}=0{,}56568… )!$
Для знакомых с понятием производной поясним: у функции $f(x)=\frac{1}{2}{\left(x+\frac{a}{x}\right)}$ производная $f'(x)=\frac{1}{2}-\frac{a}{2x^2}<\frac{1}{2}$, поэтому функция $f$ «сжимает» окрестность точки $\sqrt{a}$ более чем вдвое (в математике такие отображения и называются сжимающими).
Теорему Пифагора можно запомнить и усвоить значительно лучше, если к обычному геометрическому доказательству добавить преодоление трудностей в решении головоломки, конструкция которой основана на этой теореме. Заметим, что формула $a^2+b^2=c^2$, связывающая стороны прямоугольного треугольника, выражает равенство площадей: площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Планиметрическая теорема Бойаи—Гервина утверждает, что два равновеликих многоугольника (т. е. имеющих равные площади) равносоставлены. Последнее означает, что любой из них можно разрезать на несколько многоугольников так, что из этих частей можно сложить второй многоугольник.
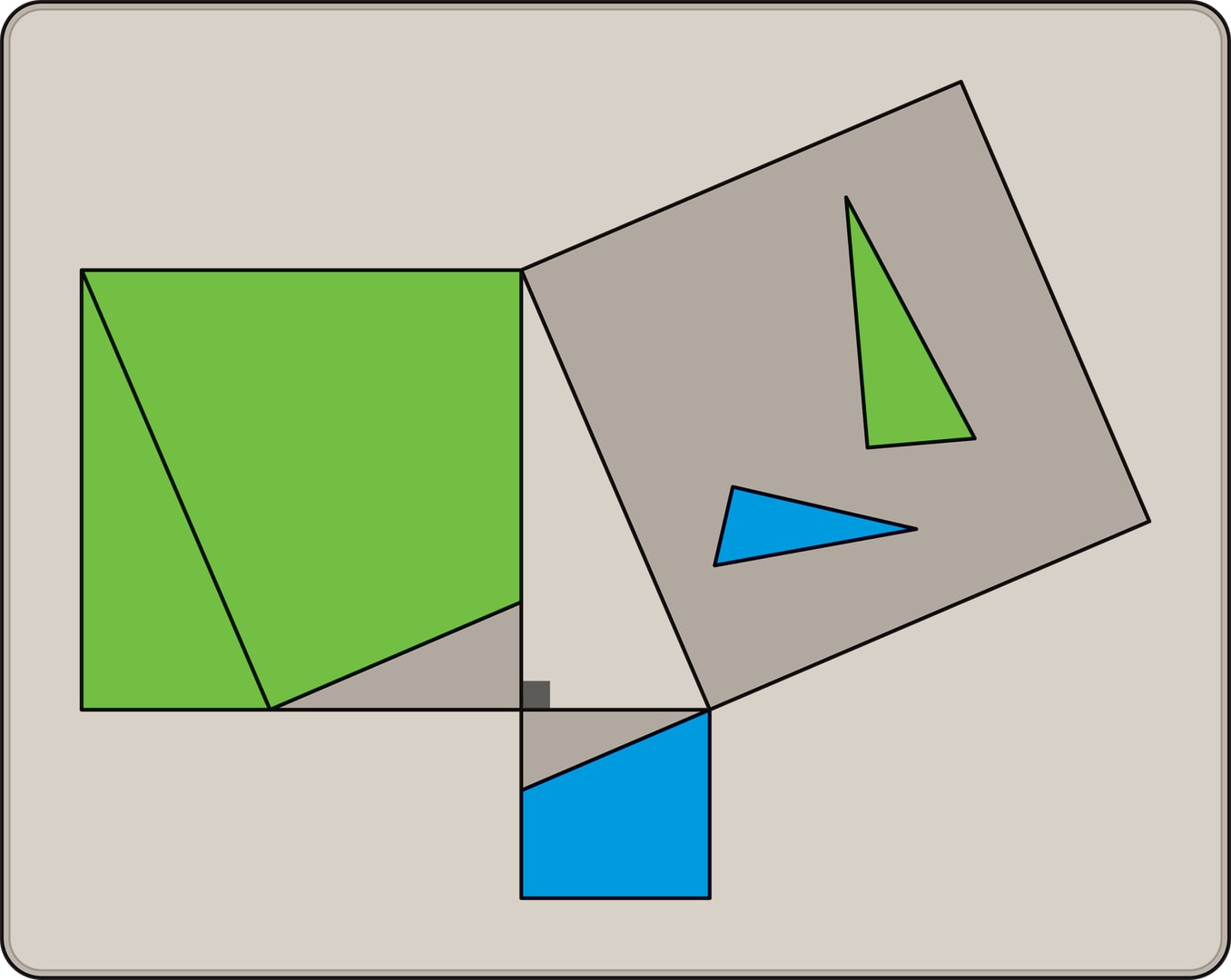
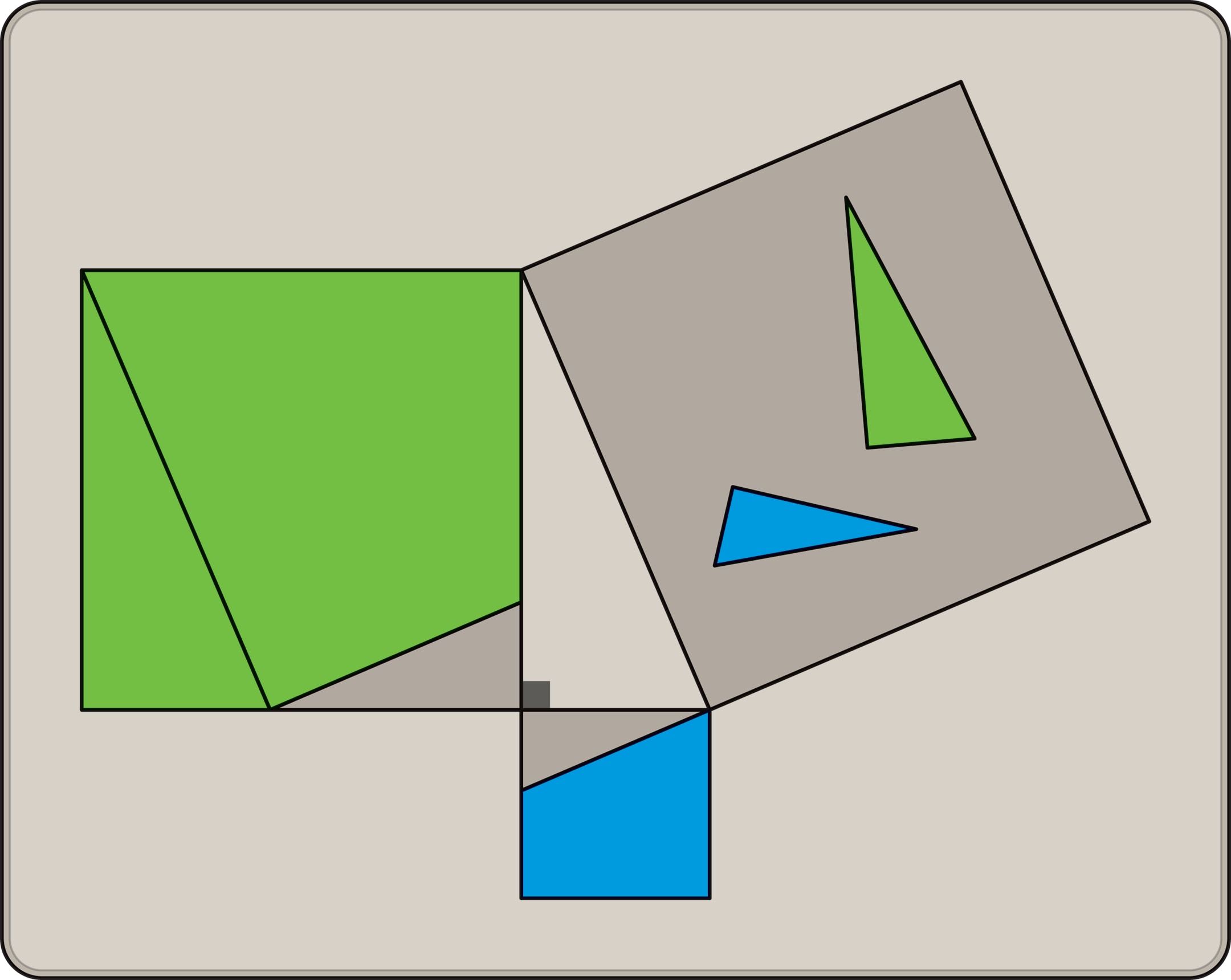
Применительно к конструкции в теореме Пифагора получаем, что квадраты, построенные на катетах, можно разрезать на части-многоугольники, из которых «складывается» квадрат, построенный на гипотенузе. Подобных разбиений множество, но самое экономное только одно, наименьшее число частей равно 5. Обратите внимание на то, что такое разбиение возможно для произвольного прямоугольного треугольника.
Головоломку проще всего изготовить из двух листов толстого картона: один будет служить основанием, на другом вырезаются три квадрата, затем листы склеиваются. Два меньших квадрата разрезаются на части. Задание — сложить из кусочков маленьких квадратов большой, без пустот и наложений элементов.
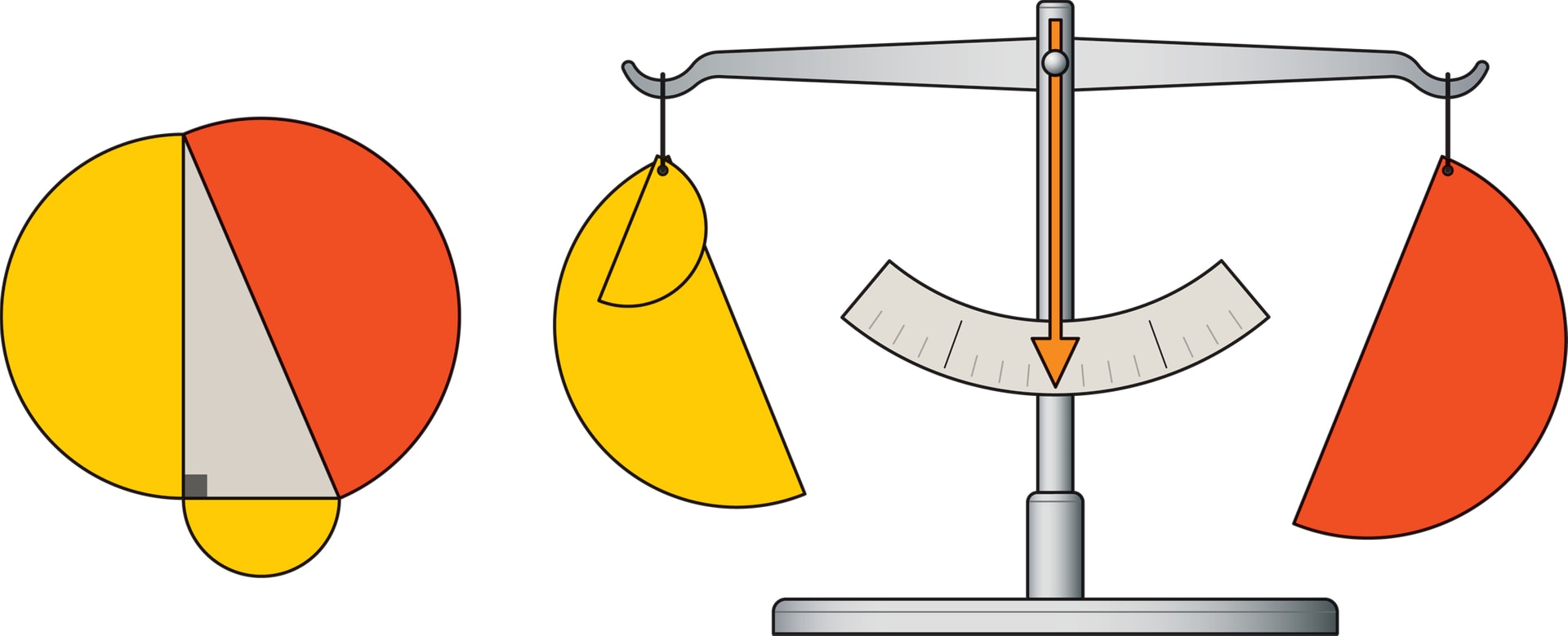
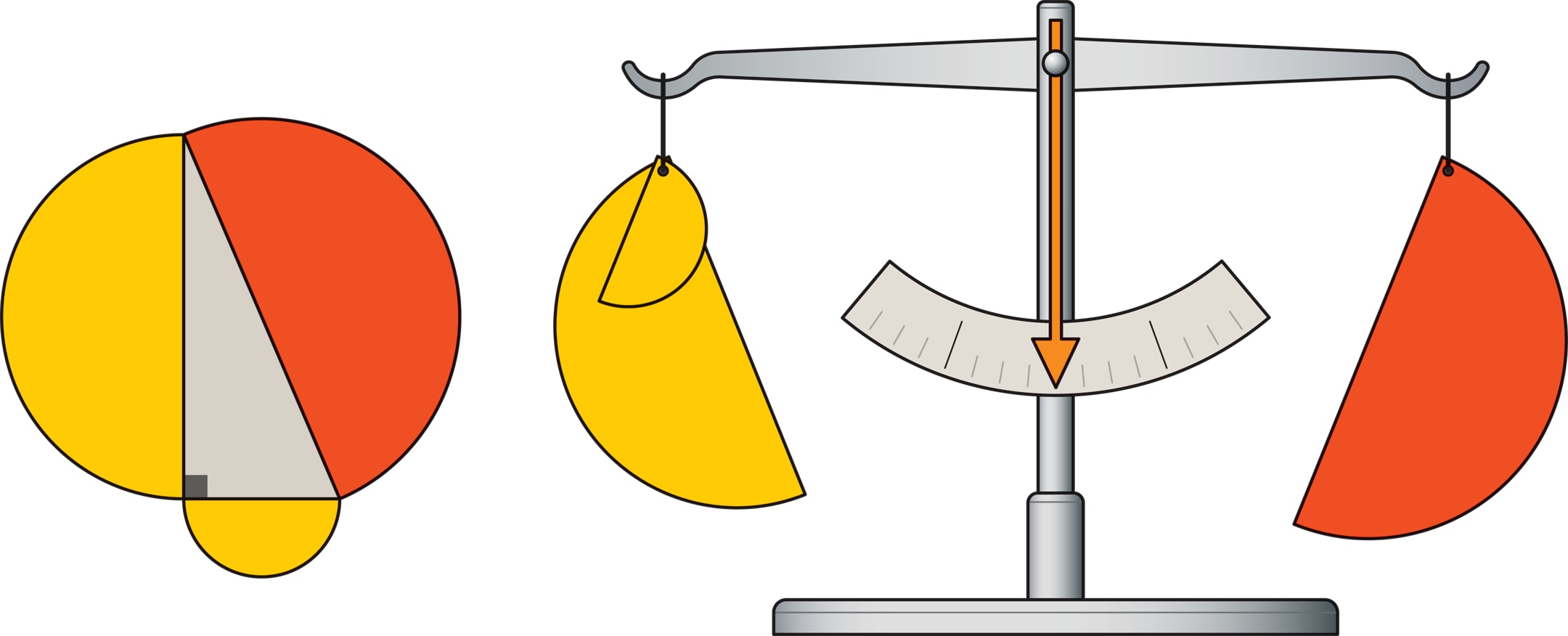
Ещё один тип учебных пособий, иллюстрирующих теорему Пифагора, связан со взвешиванием «изготовленных» геометрических фигур.
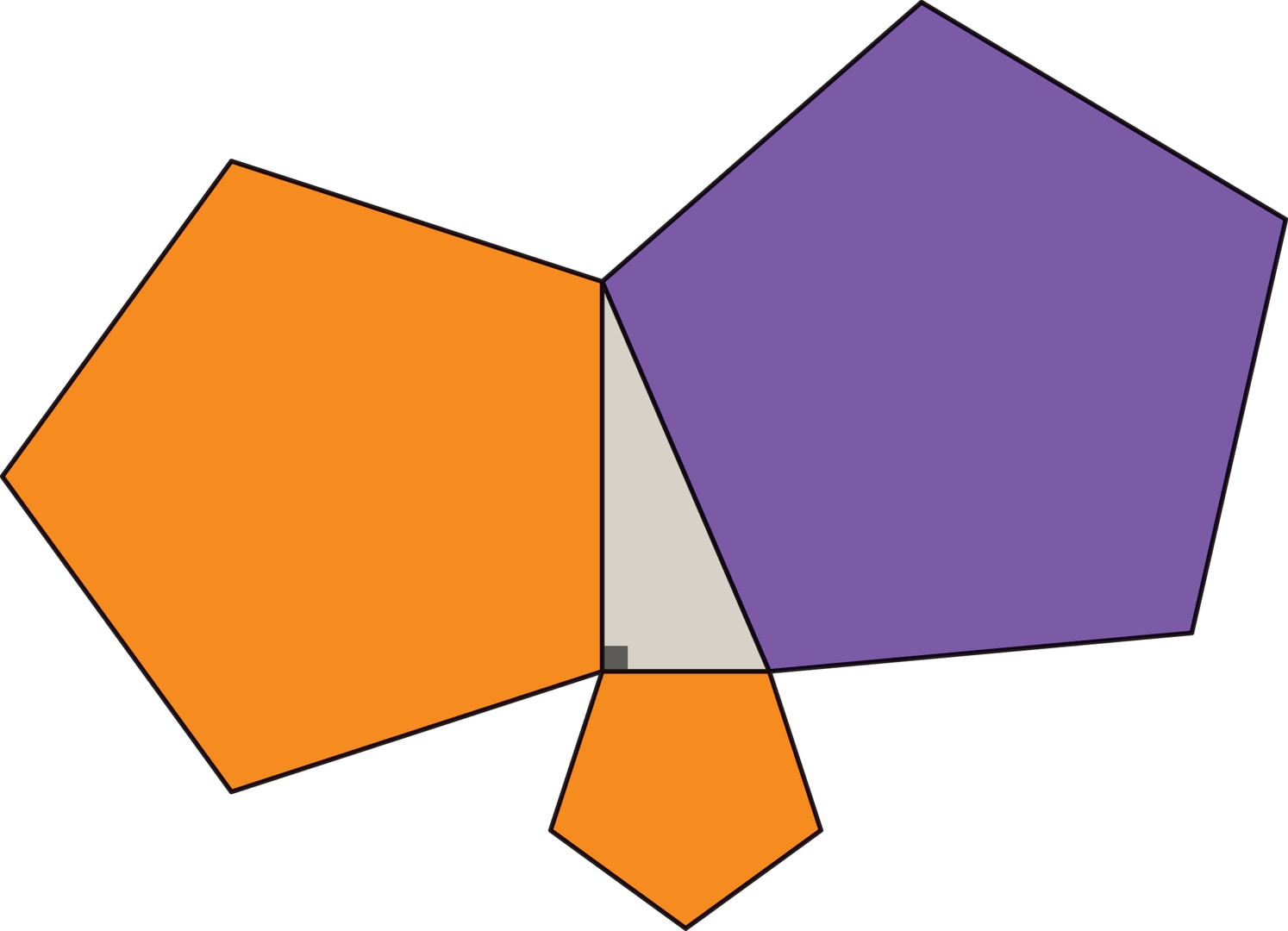
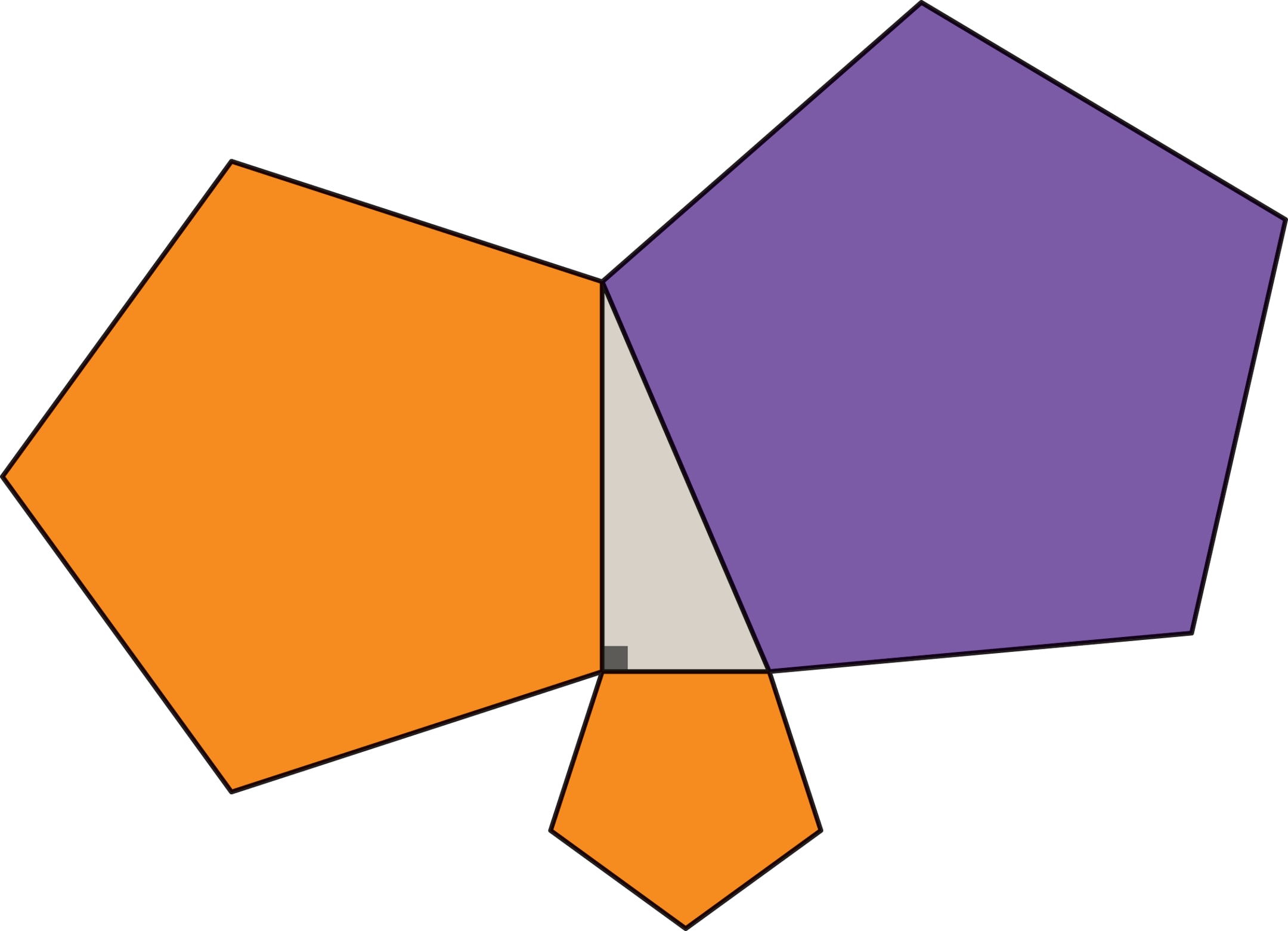
Чтобы теорема Пифагора стала утверждением о равенстве площадей, на сторонах прямоугольного треугольника были построены квадраты. Но если их заменить однотипными подобными правильными многоугольниками или полукругами, то сумма площадей на катетах также будет равна площади фигуры на гипотенузе. Например, для полукругов равенство площадей $$ \frac{π}{8} a^2 + \frac{π}{8} b^2= \frac{π}{8} c^2 $$
получается из теоремы Пифагора умножением элементов формулы на число $\frac{π}{8}$.
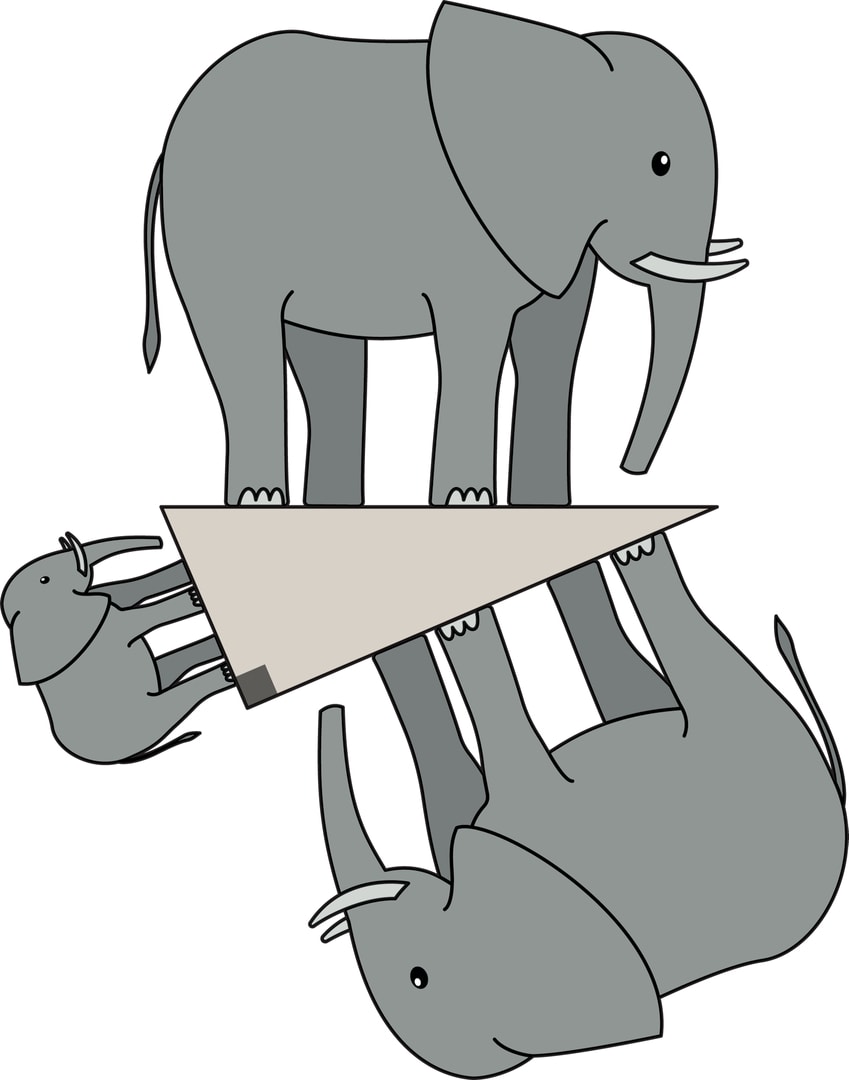
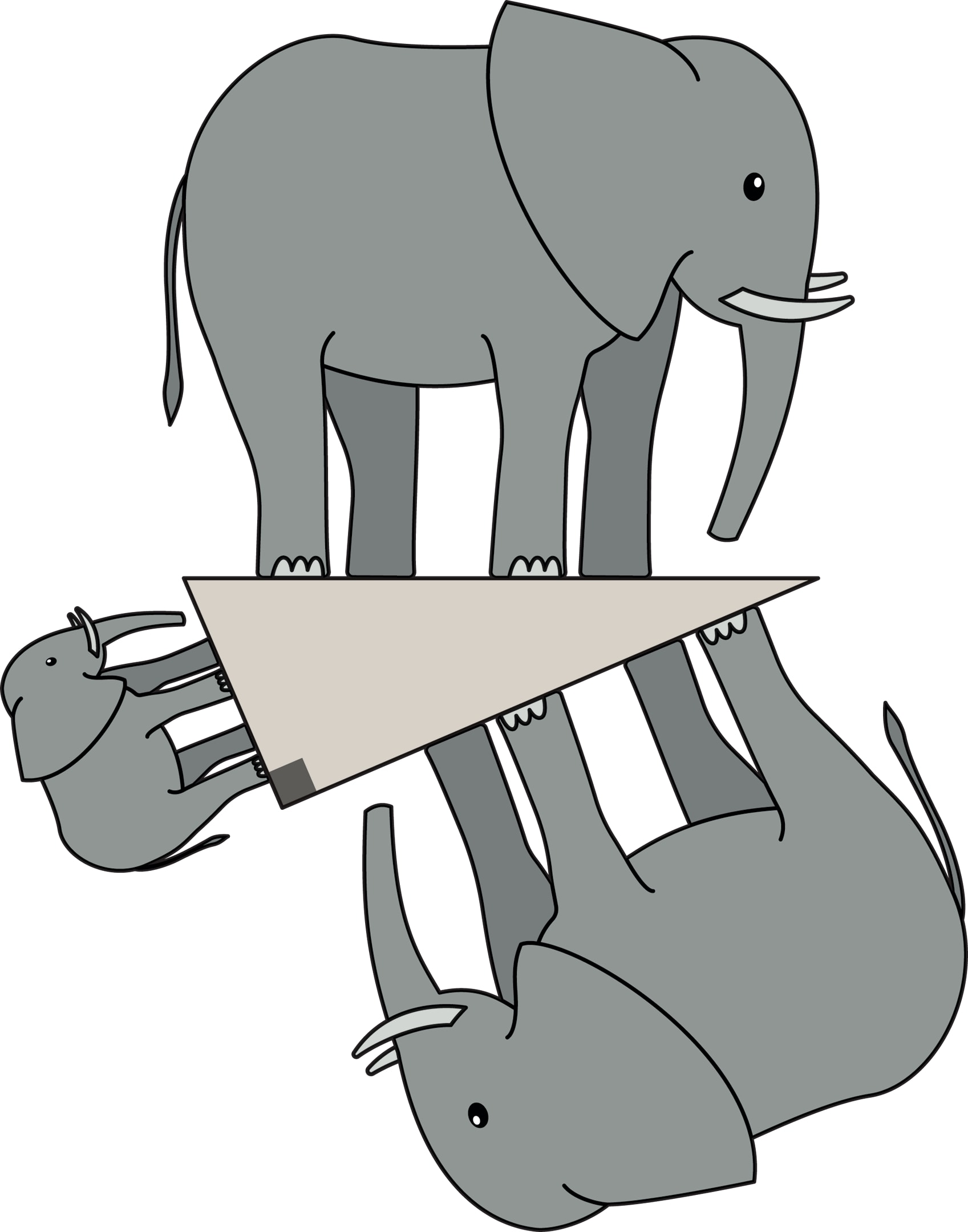
А вот если взять трёх «подобных» слонов, стоящих на сторонах треугольника и «вписанных» в квадраты, то готовой формулы для площадей таких фигур нет, но из подобия фигур можно вывести, что по площади каждая фигура занимает в своём квадрате одну и ту же часть: $$ S_a+S_b=ka^2+kb^2=kc^2=S_c. $$
Можно проверить справедливость этих выводов опытным путём, взвесив на весах (например, простейших рычажных) эти фигуры, и убедиться, что $S_a+S_b=S_c$. Причём начать можно с самих квадратов со сторонами $a$, $b$ и $c$.
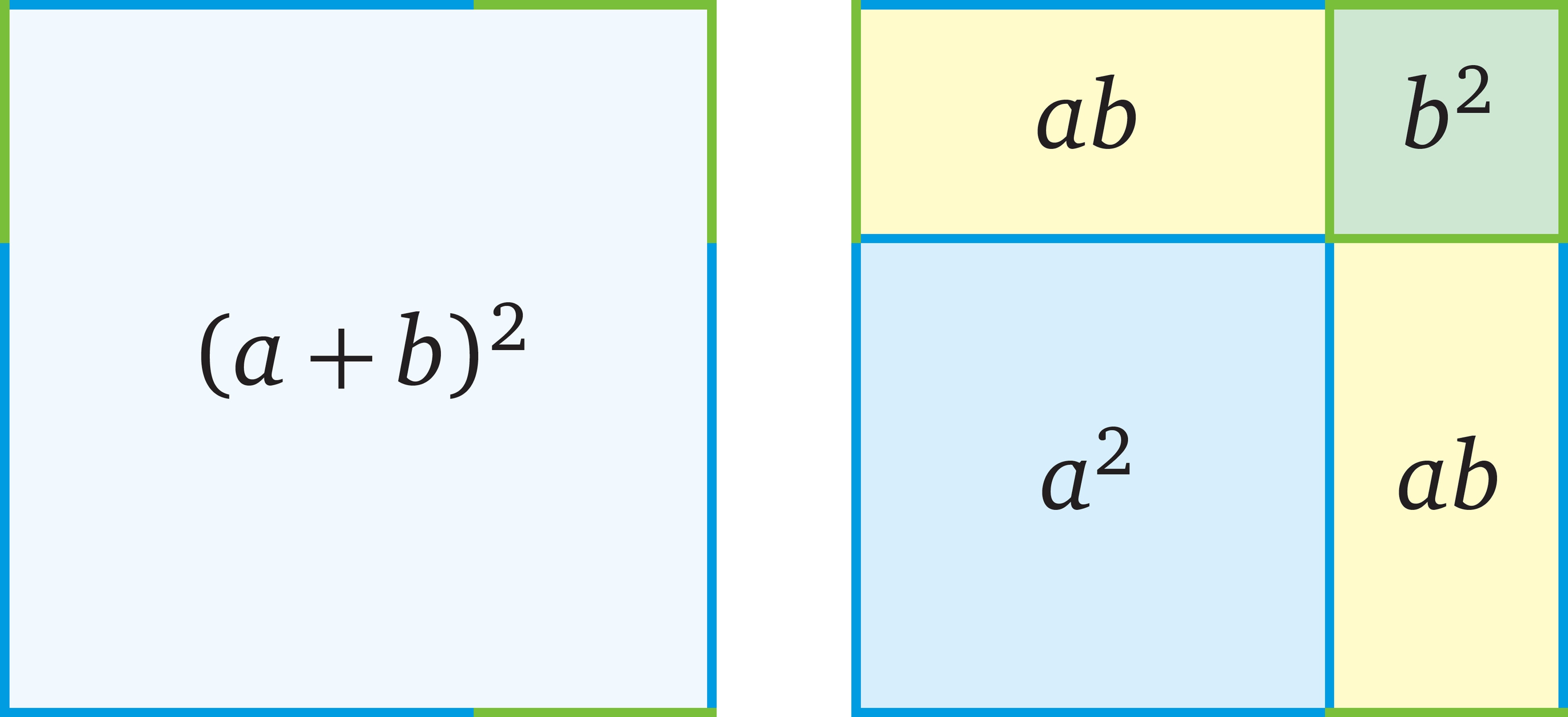
Иногда алгебраические формулы удаётся столь наглядно представить геометрически, что всё «доказательство» заключается в рисунке с подписью «Смотри!» (в стиле древних индийских математиков).
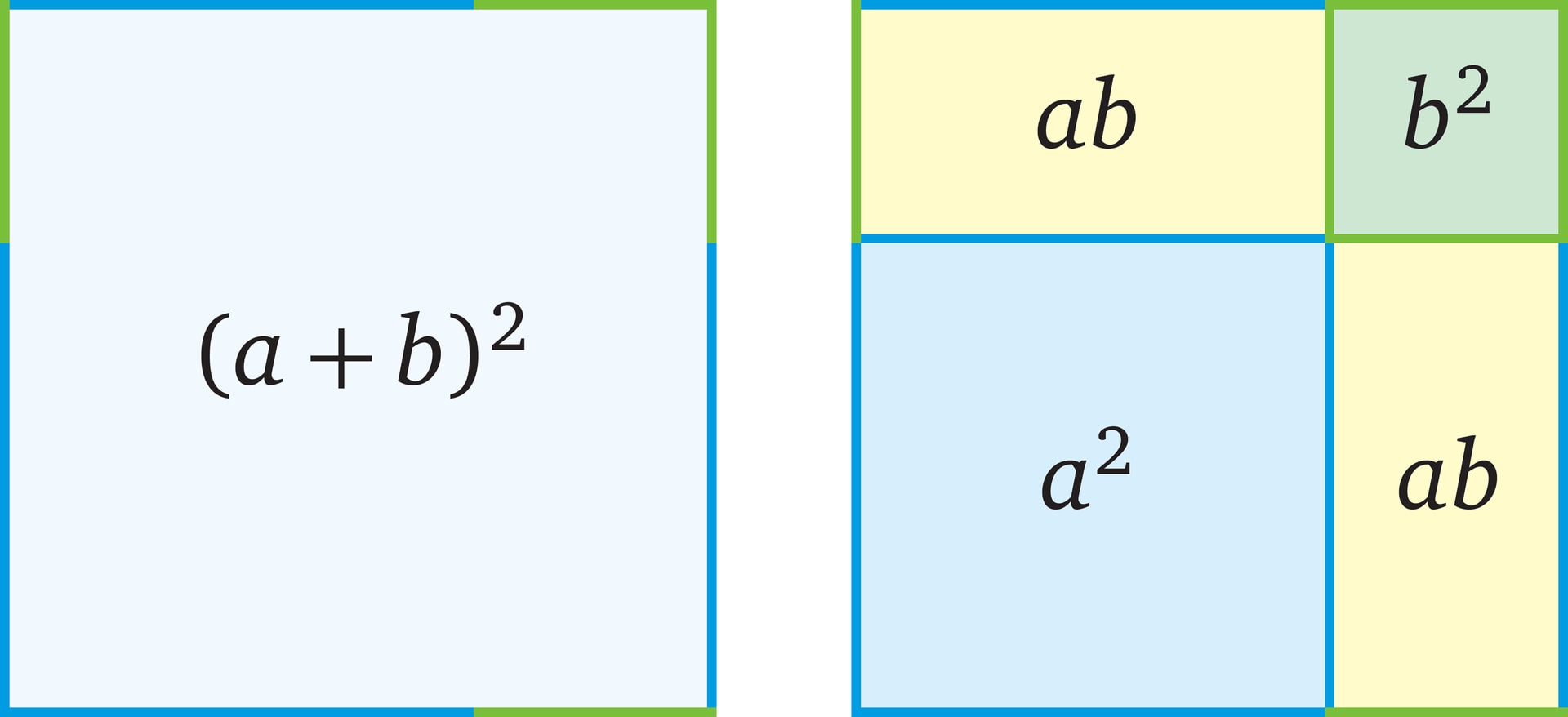
Объяснить геометрически можно и использованную в статье формулу «сокращённого умножения» для квадрата суммы $$ (a+b)^2=a^2+2ab+b^2. $$
Жан‐Жак Руссо в «Исповеди» писал:
Когда я в первый раз обнаружил при помощи вычисления, что квадрат бинома равен сумме квадратов его членов и их удвоенного произведения, я, несмотря на правильность произведённого мною умножения, не хотел этому верить до тех пор, пока не начертил фигуры.
Перельман Я. И. Занимательная геометрия на вольном воздухе и дома. — Л.: Время, 1925. — [Подходит и любое издание книги Я. И. Перельмана «Занимательная геометрия»].
Литцман В. Теорема Пифагора. — Одесса: Mathesis, 1912. — [Переиздания: 1935, 1960].
Интерактивная головоломка «Теорема Пифагора»