Выбор оптимального варианта действий — одна из главных задач в современной жизни, которая становится всё более сложной и динамичной. Среди рекомендаций, предлагаемых математическими моделями, есть приёмы, для понимания которых достаточно школьных представлений о теории вероятностей и комбинаторике.
Метод «выбора из двух» — пример соединения эффективности и простоты. Область применения — задачи о балансировке нагрузки из раздела математики с актуально звучащим названием: теория очередей.
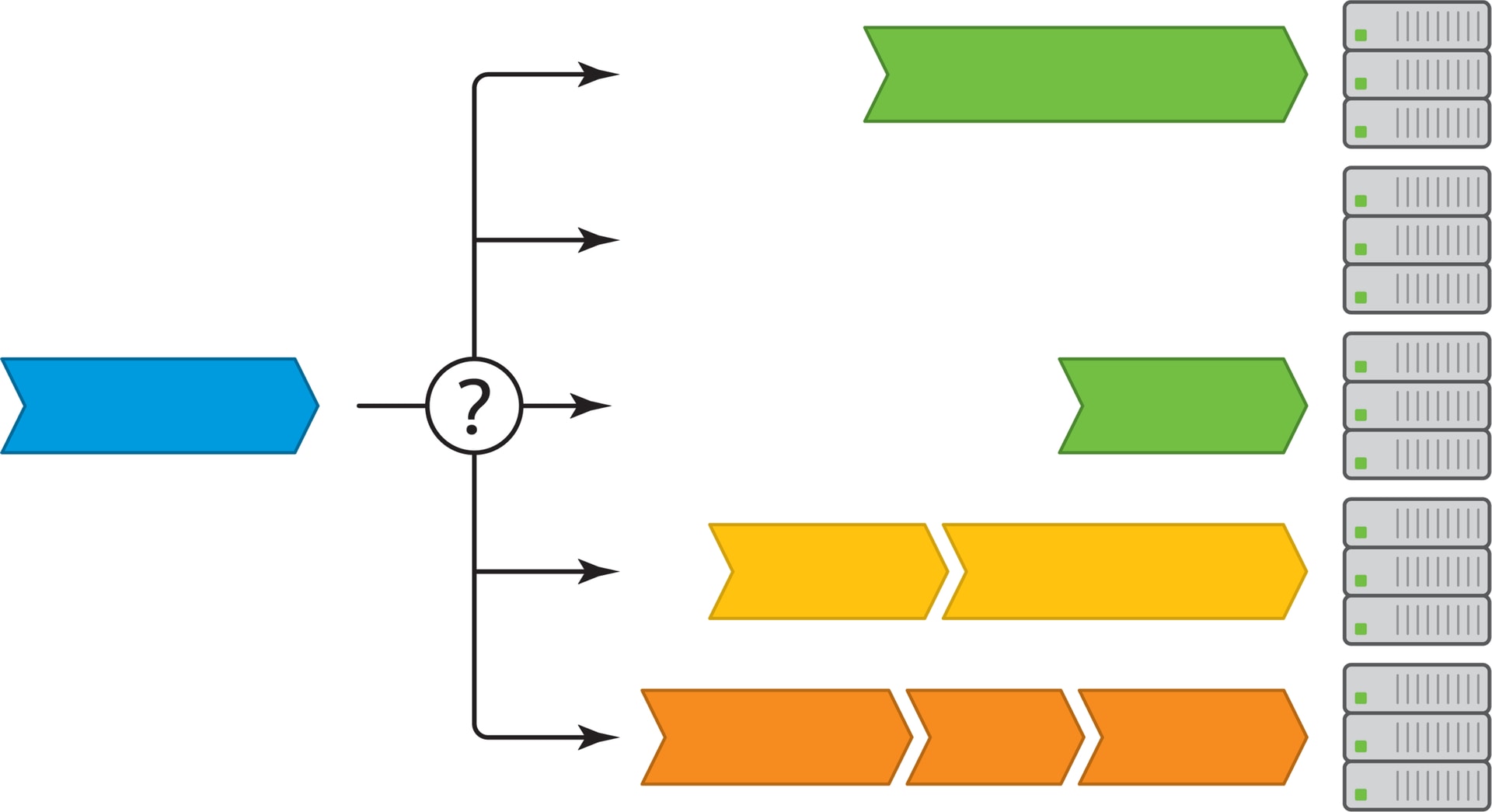
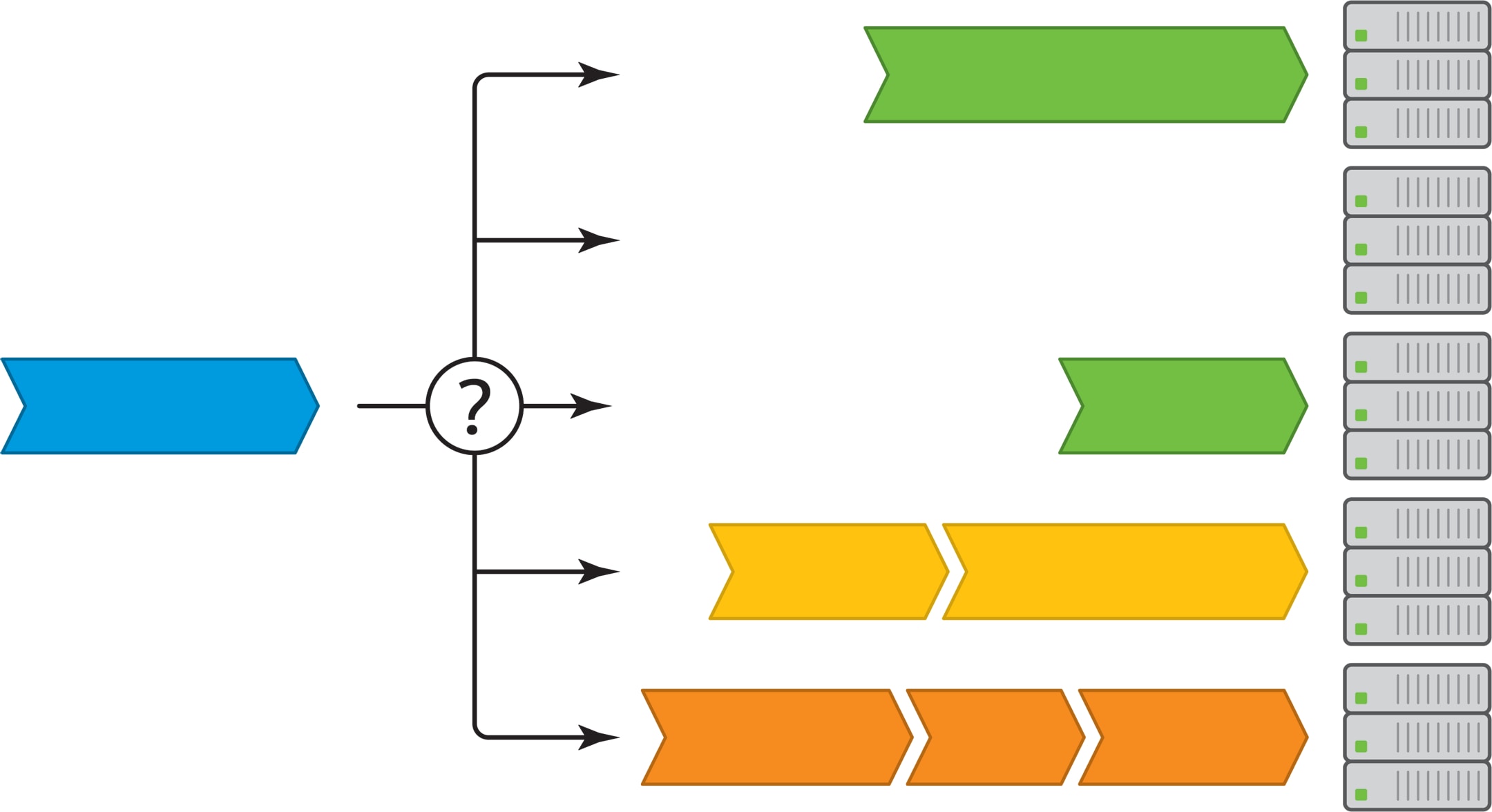
Реальная очередь может состоять как из людей в кассы супермаркета, так и из запросов к серверам поисковой системы. В супермаркете посетитель выбирает очередь по её длине и количеству товаров в корзинах покупателей. Поступающий в поисковую систему запрос тоже хочется направить к серверу с короткой очередью. Однако, если серверов очень много, то непрерывный опрос всех о длине очереди сделает систему неработоспособной.
Другая крайность — выбор сервера наугад, — очевидно, неоптимальна. Но если выбрать наугад два сервера и, узнав о длине очереди к каждому, направить запрос на менее загруженный, то практически отсекаются самые длинные очереди и увеличиваются шансы на попадание в самые короткие.
Продемонстрируем метод «выбор из двух» на примерах. Если самая длинная очередь только одна, то при выборе из двух попадание в неё исключается.
Если серверов много, а самых загруженных — пятая часть, то вероятность попадания в «плохую» очередь не исключается, но мала и примерно равна произведению вероятностей $\frac15\cdot \frac15=\frac1{25}$. Аналогично, если самых свободных серверов тоже пятая часть, то вероятность попасть в «хорошую» очередь равна $\frac9{25}$.
Несмотря на простоту идеи, основанные на ней методы получили распространение и развитие только в недавнее время. А вы, читатель, оказавшись в супермаркете с десятками касс, выбирайте наугад пару очередей и направляйтесь к более короткой, меньшему из двух зол!