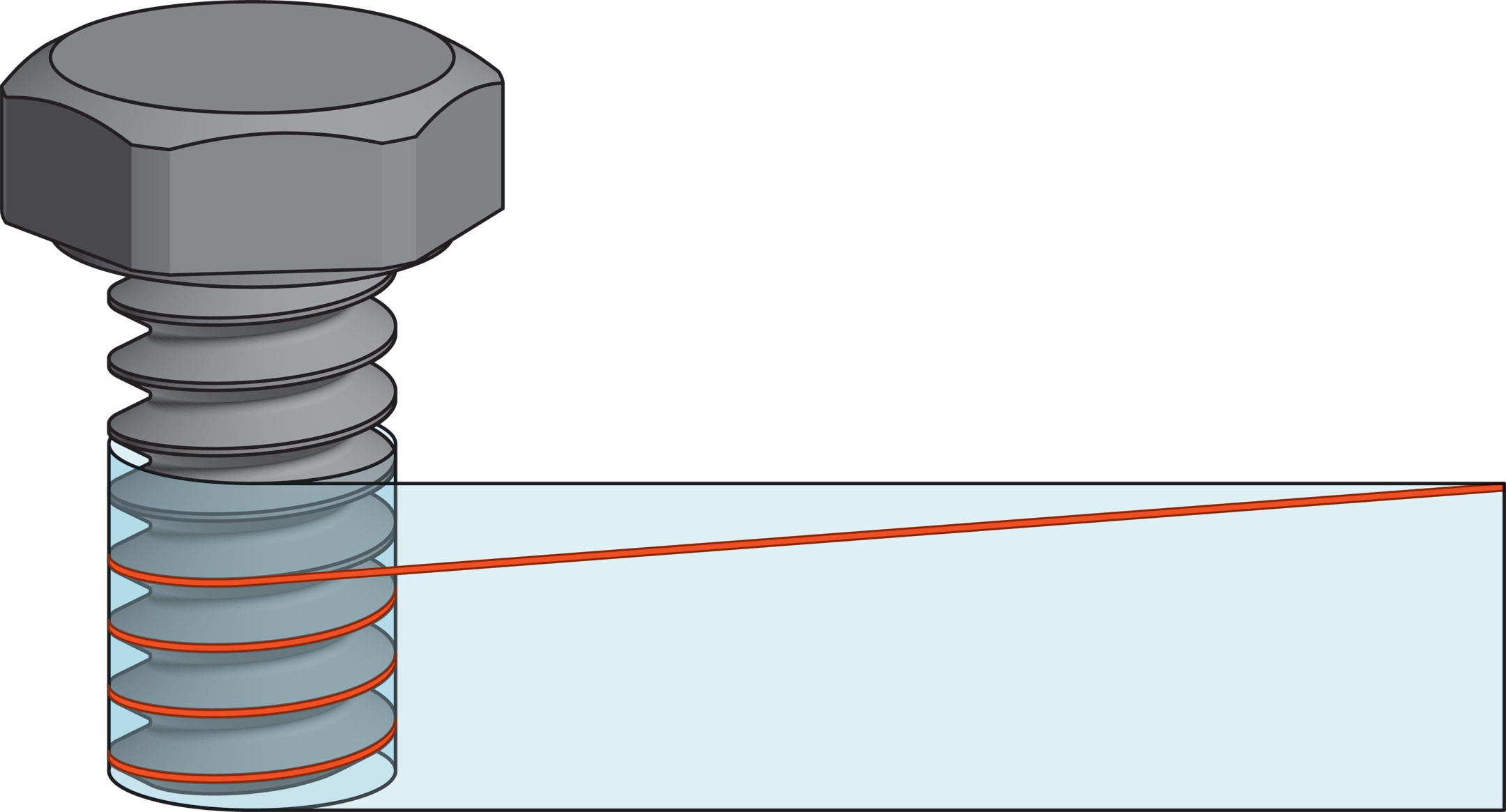
Лёгкость, с которой гайка накручивается на болт с такой же резьбой, подсказывает, что резьба эта одинакова по всей длине болта и глубине гайки, а математическая суть устройства — использование кривой, которая может скользить сама по себе. Эта замечательная кривая называется винтовой линией. Можно считать, что на внутренней поверхности гайки «проложена лыжня» в виде винтовой линии, и по накатанному пути скользит выступающая часть винта, имеющая форму такой же линии.
Формально винтовой линией (цилиндрической) называется линия, описываемая точкой, которая вращается с постоянной угловой скоростью вокруг неподвижной оси и одновременно перемещается вдоль этой оси с постоянной скоростью.
Наглядное представление о винтовой линии можно получить, намотав на цилиндр прямоугольный прозрачный лист с проведённой диагональю.
У хороших (достаточно гладких) кривых в трёхмерном пространстве есть две базовые характеристики — кривизна и кручение. Кривизна — это локальная «скорость» искривления линии (определяется радиусом окружности, дуга которой наилучшим образом приближает небольшой отрезок кривой, содержащий данную точку). Кручение — «скорость», с которой кривая стремится не быть плоской: небольшой отрезок кривой в первом приближении «лежит» в некоторой плоскости, а вот то, насколько он «хочет» покинуть эту плоскость, и сообщает кручение. Замечательно, что для достаточно гладких кривых кривизна и кручение полностью определяют форму линии.
У винтовой линии кривизна и кручение постоянны, вследствие этого её «устройство» всюду одно и то же. Именно поэтому отрезок винтовой линии может скользить вдоль неё самой.
А поскольку постоянство кривизны и кручения однозначно определяет кривую, то винтовая линия — единственная кривая, которая может скользить сама по себе. И при решении инженерных задач, в которых наличие такого свойства желательно или даже необходимо, без винтовых линий не обойтись.
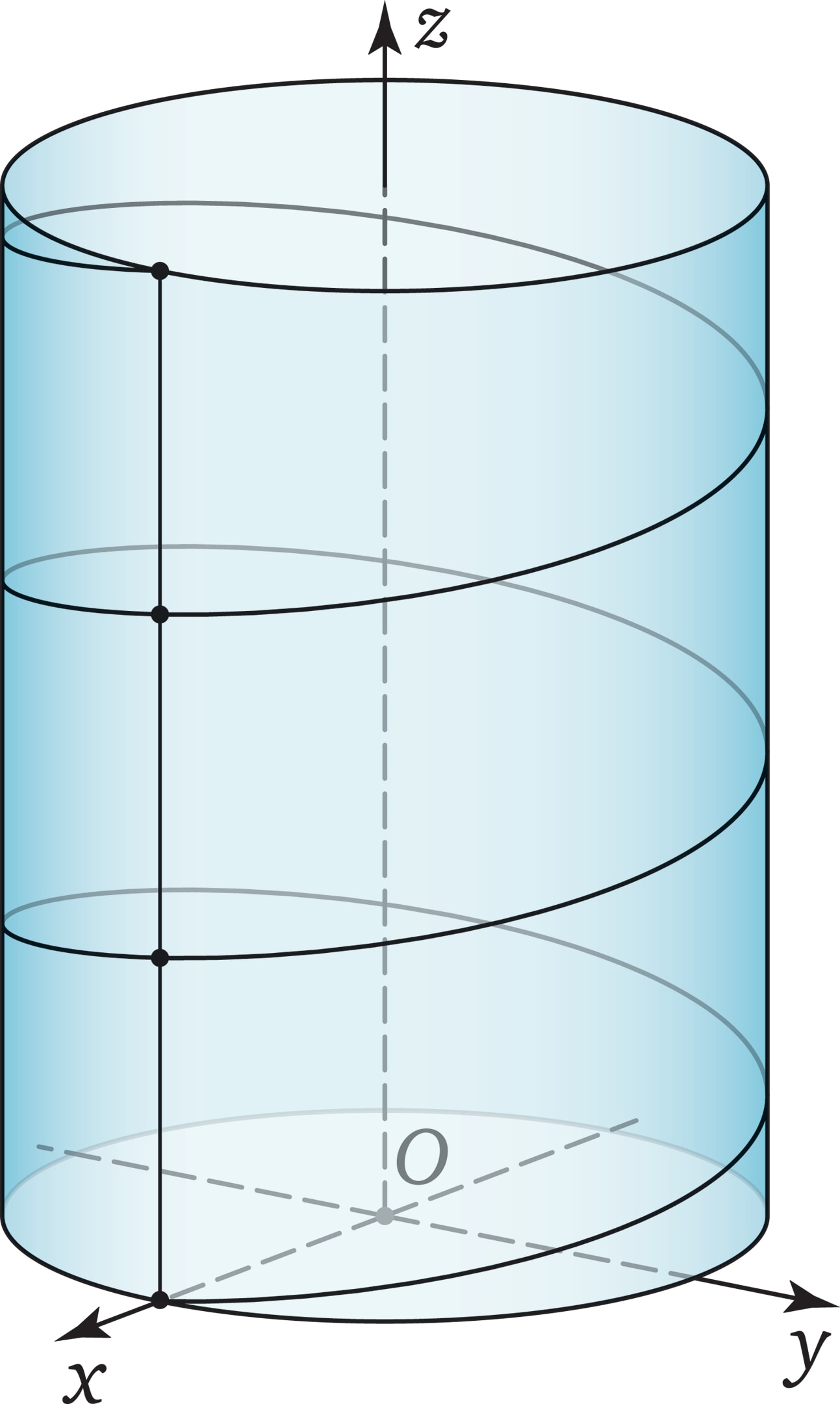
Параметрические уравнения винтовой линии — это удобные технически и наглядные формулы. Если взять прямой круговой цилиндр, заданный в прямоугольной декартовой системе координат уравнением $x^2+y^2=a^2$, то можно проверить, что уравнения $$ x=a\cos t, \quad y=a\sin t, \quad z=ht $$
будут задавать винтовую линию. Действительно, эта линия будет лежать на поверхности цилиндра, так как $$x^2+y^2=(a\cos t)^2 + (a\sin t)^2 = a^2.$$
Проекция точки $(a\cos t; a\sin t; ht)$ на плоскость $Oxy$ имеет координаты $(a\cos t; a\sin t; 0)$. Это означает, что проекция «бежит» по окружности, $t$ можно считать углом поворота вектора $(x;y)$ вокруг точки $O$, скорость этого вращения постоянна. Формула $z=ht$ «сообщает», что и движение вдоль оси $Oz$ происходит с постоянной скоростью.
Обратите внимание на то, что в уравнении цилиндра отсутствует переменная $z$, благодаря этому окружность $x^2+y^2=a^2$ из плоскости $Oxy$ скользит по «бесконечному лифту» вдоль оси $Oz$.
Для винтовой линии можно дать эквивалентное геометрическое определение: это линия на поверхности цилиндра, которая пересекает все образующие цилиндра под равными углами.
Прямую и окружность можно рассматривать как вырожденные, предельные случаи винтовой линии, что следует и из определений винтовой линии, и из её уравнений. Как и в «общем» случае, отрезок может скользить по прямой, а дуга — по своей окружности. Это давно знают оружейники: клинок и ножны в плоском случае могут быть только двух видов — или прямолинейными, или дугами одной окружности.
Представление о винтовой линии как о диагонали прямоугольной плёнки, намотанной на цилиндр, приводит к интересным практическим выводам. Например, кратчайшая линия, соединяющая две точки на поверхности цилиндра, — дуга винтовой линии. В предельных случаях это отрезок образующей (если точки лежат на одной образующей) или дуга окружности (если точки лежат на одной окружности).