В кинотеатре зритель сидит перед экраном, за его спиной находится проектор, «передающий» на экран готовую картинку. Схожим образом происходит и просмотр природной картины «Радуга», но есть принципиальное отличие. На «экран» в виде стены дождя Солнце-проектор светит белыми лучами, а перед наблюдателем вспыхивает яркая многоцветная радуга.
В объяснение формы радуги и её расположения на небе основной вклад внёс Рене Декарт (в 1637 году издано «Рассуждение о методе» с замечательными рисунками), а Исаак Ньютон «раскрасил» радугу (его «Оптика» была издана в 1704 году). Декарт свои выводы о механизме образования радуги сделал на основе результатов тысяч проведённых опытов по изучению прохождения солнечных лучей через круглую колбу, наполненную водой. Ньютон, изучив разложение белого света на цветовые составляющие при прохождении через стеклянную призму, смог объяснить цветовую гамму радуги и порядок цветов в ней.
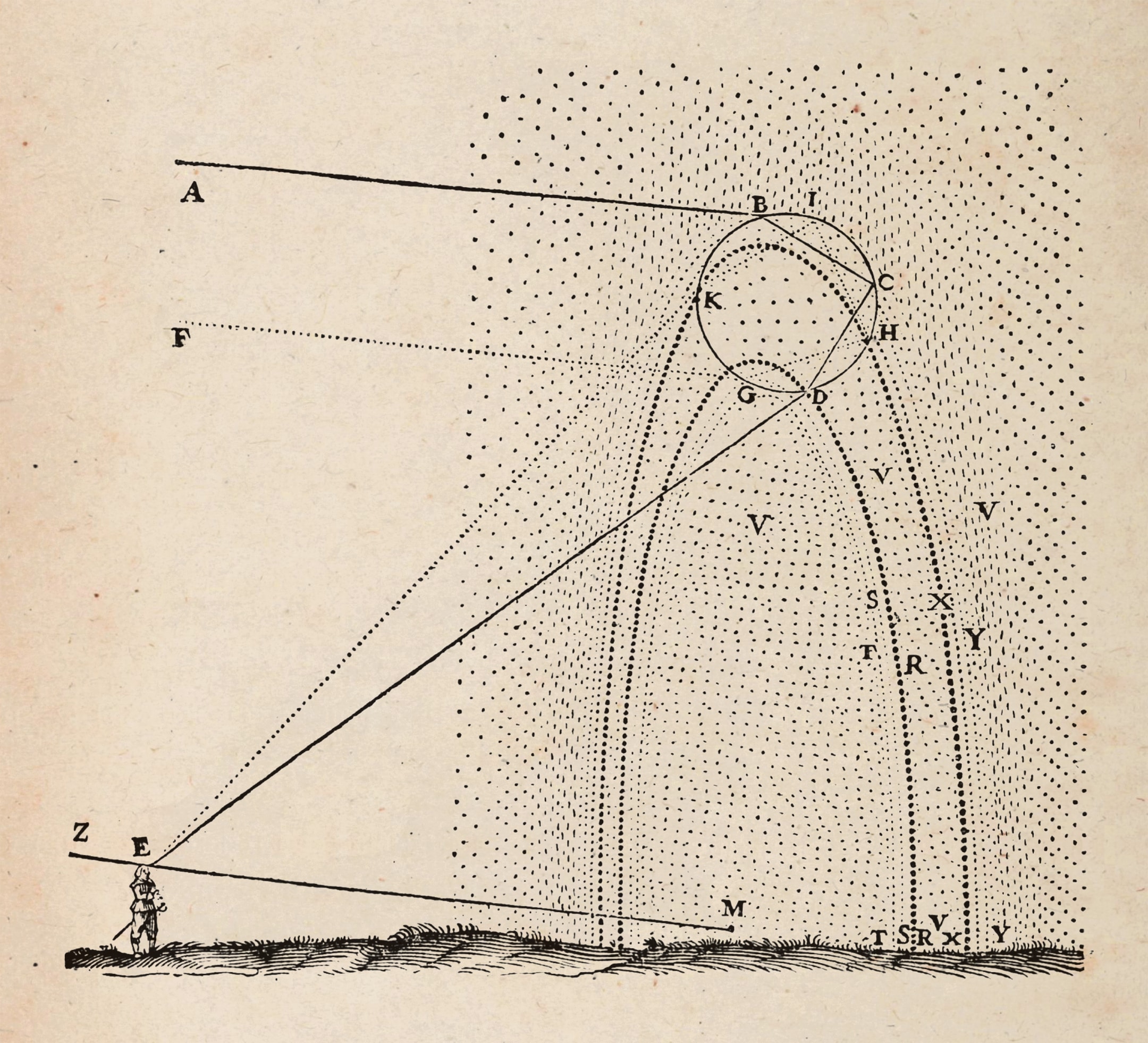
Выводы как Декарта, так и Ньютона можно получить, изучая прохождение солнечных лучей через одну дождевую каплю. В первом приближении можно считать, что капля имеет форму шара, а приходящие от далёкого Солнца лучи параллельны.
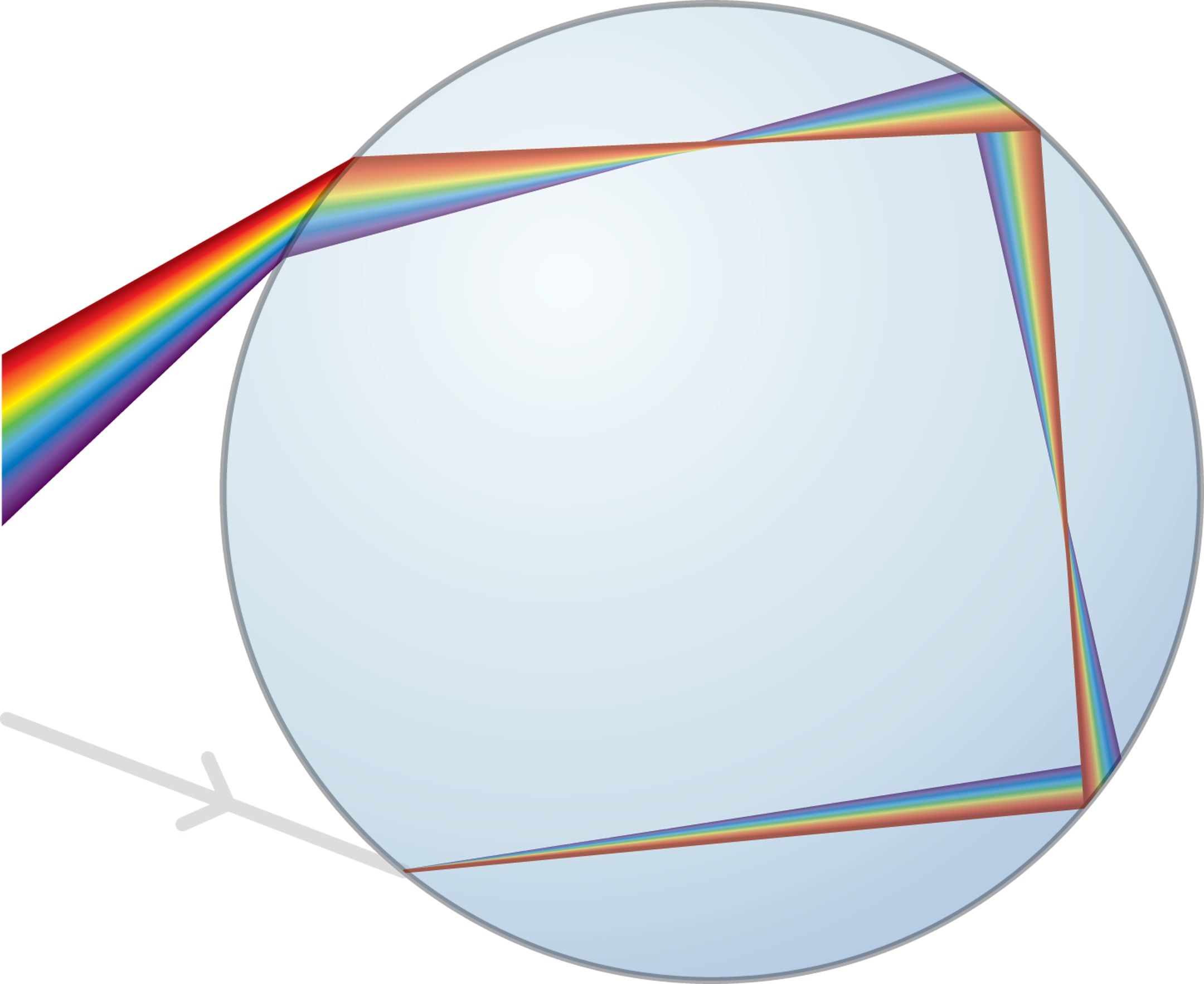
При переходе лучей через границу двух сред — как из воздуха в каплю, так и из капли в воздух — происходят два процесса: отражение и преломление. Каждая такая развилка порождает новые лучи.
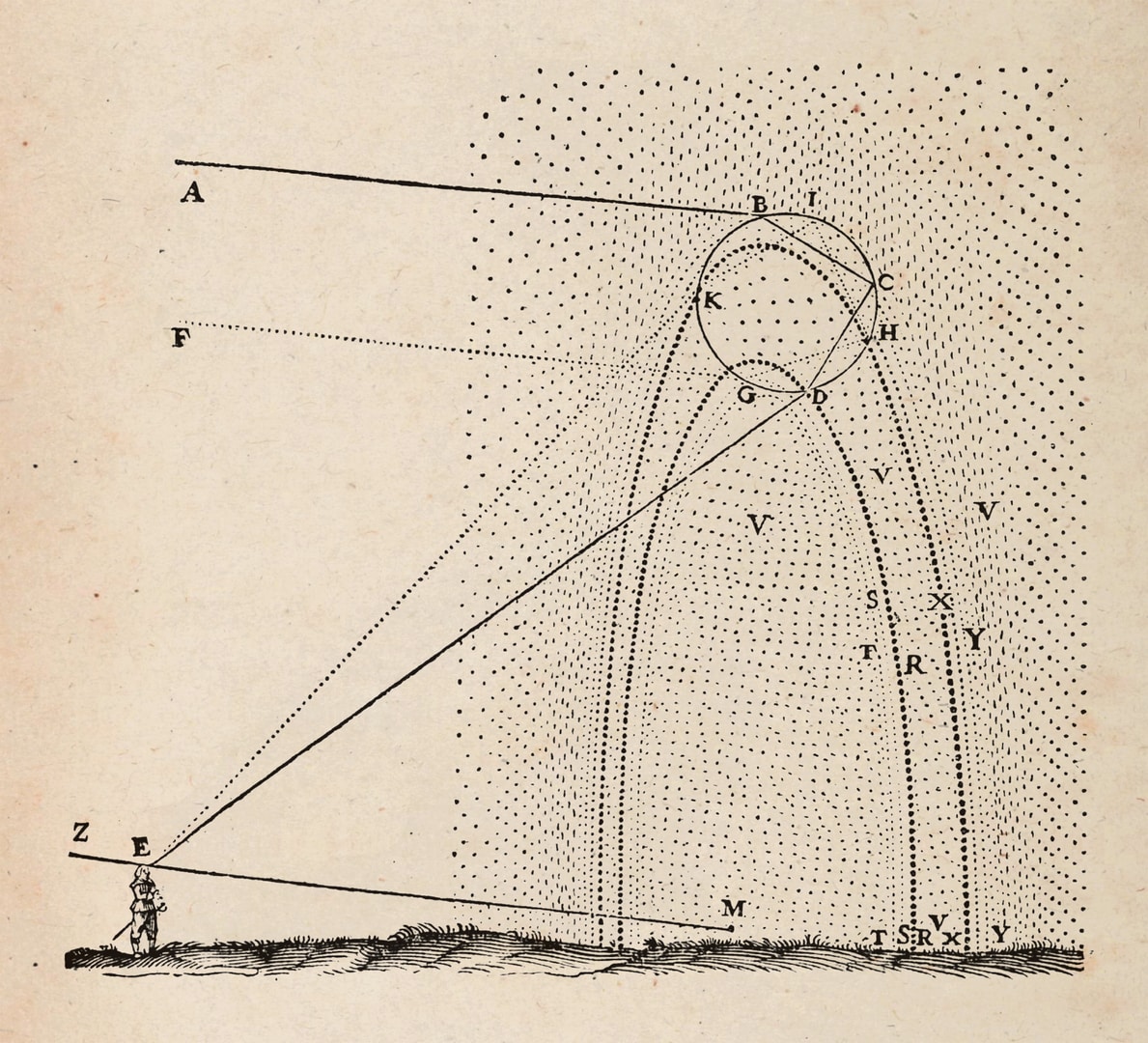
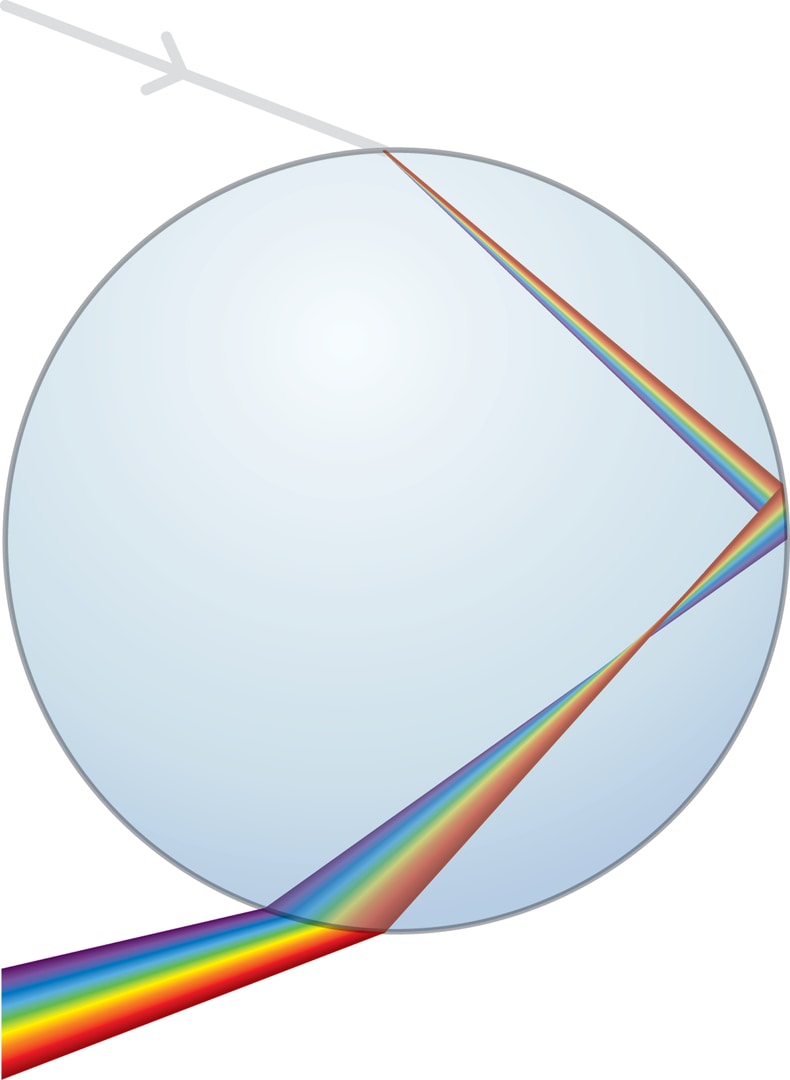
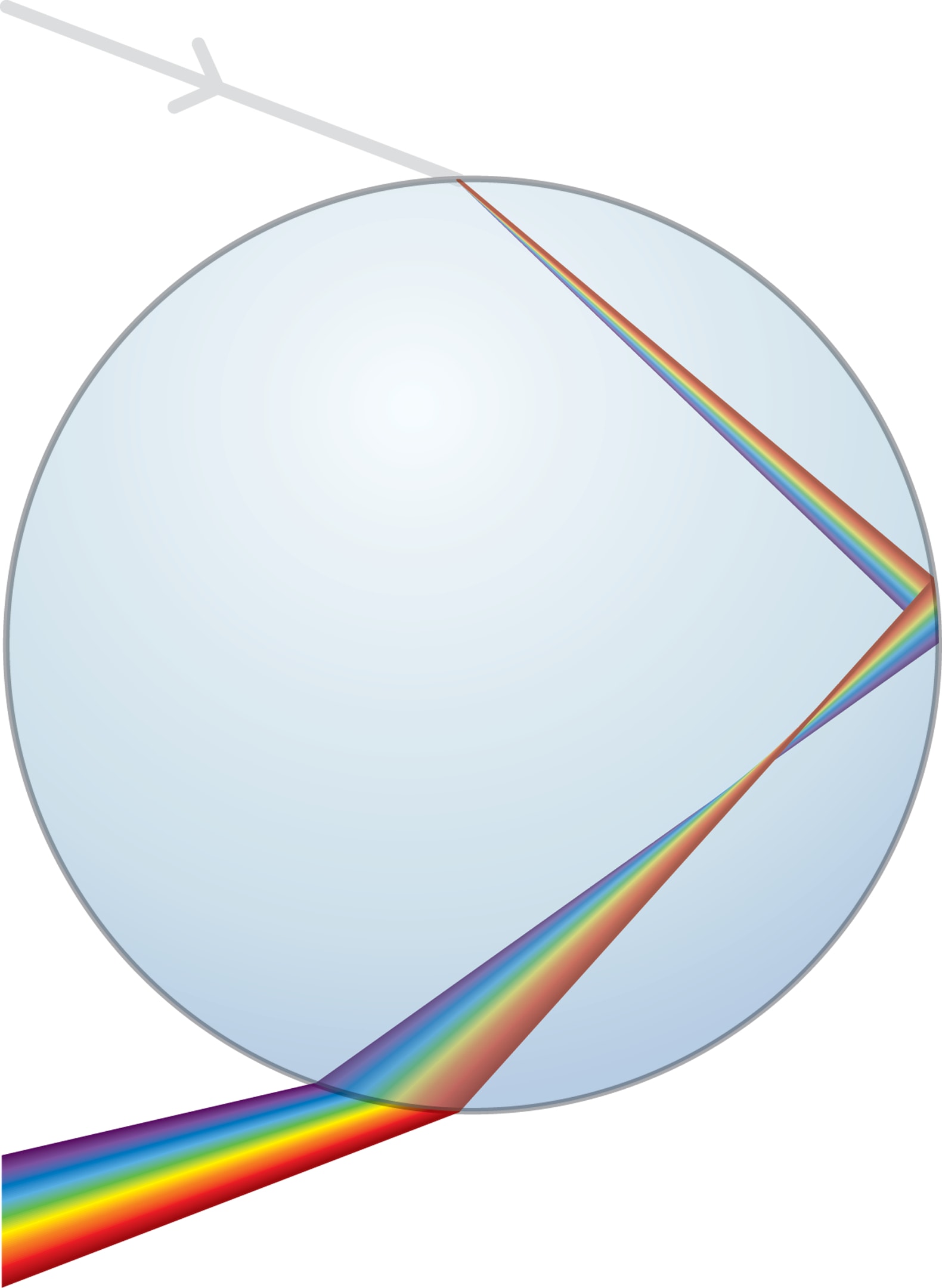
Рассмотрим ход лучей в «естественной» вертикальной плоскости. Будем следить только за теми лучами, которые, попадая в глаз наблюдателя, образуют первую радугу. Солнечные лучи падают на верхнюю половину капли и при переходе границы «воздух — капля» преломляются, изменяя направление движения (в воде, как в более плотной среде, лучи отклоняются в сторону нормали к границе). Причём каждый солнечный луч при переходе границы капли расщепляется на пучок составляющих его разноцветных лучей (спектр). Объясняется это тем, что у лучей разного цвета коэффициенты преломления различны. Здесь капля воды выступает в роли призмы из опытов Ньютона по разложению солнечного света на цветовые составляющие.
Затем цветные лучи отражаются от «дальней» стенки и ещё раз преломляются при выходе из капли.
Спектр солнечного света — непрерывное разноцветье с плавными переходами, от красного до фиолетового. Традиционно, вслед за Ньютоном, выделяют семь областей спектра, названия которых знакомы всем по повседневной жизни: красный, оранжевый, жёлтый, зелёный, голубой, синий, фиолетовый.
Маршрут путешествия каждой из цветовых составляющих белого луча, от красной до фиолетовой, можно представить наглядно.
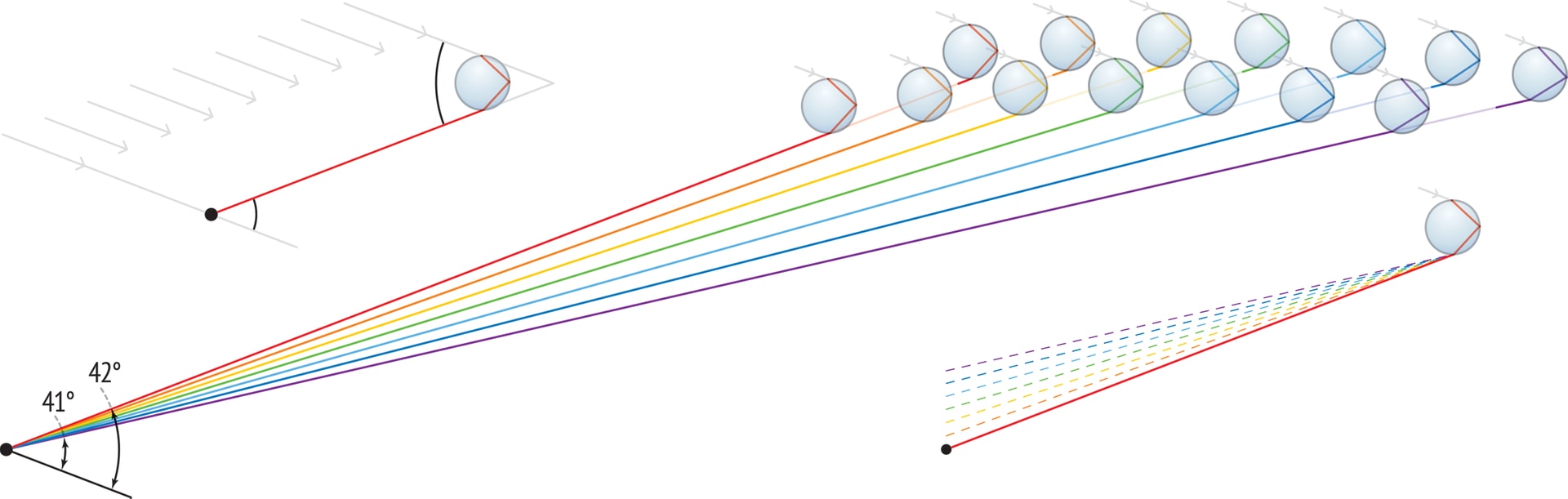
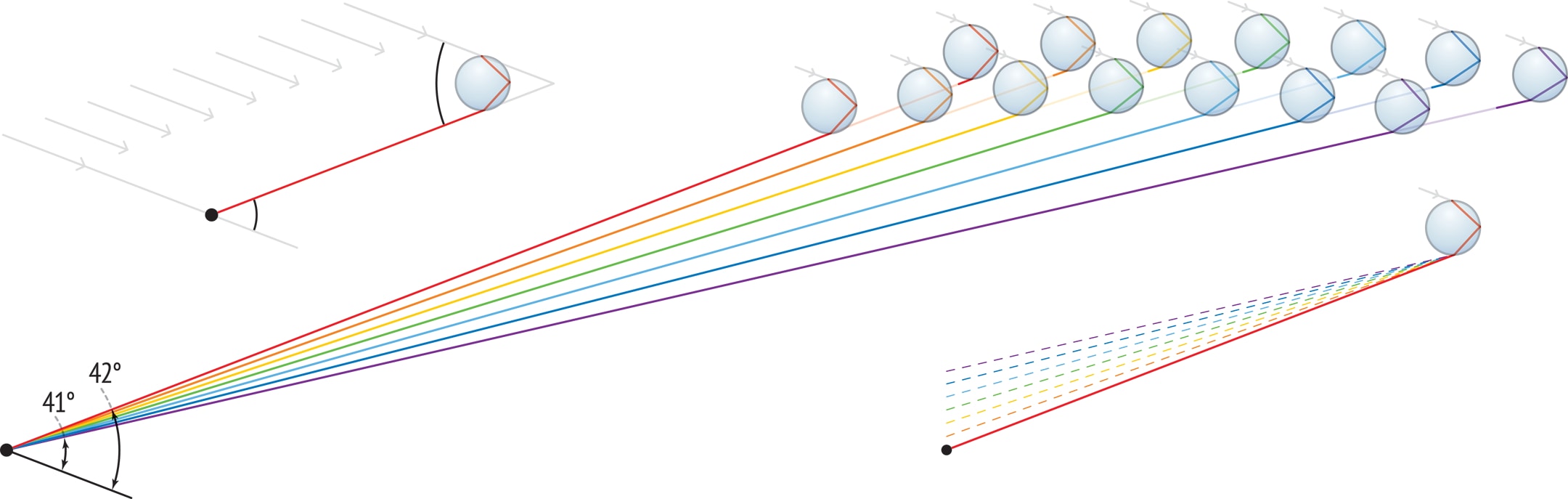
Например, красные лучи, выходящие из капли после преломления — отражения — преломления, составляют веер лучей, образующих с направлением на Солнце углы от $0°$ до $42°$. Эти значения — результат опытов, и вычислений, проделанных ещё Декартом. Но направление с углом выхода $42°$ (точнее, $42°\ 22'$) — особое, здесь наблюдается концентрация, накопление красных лучей; интенсивность излучения красного цвета в этом направлении наибольшая.
Аналогично обстоит дело с другими цветами спектра. Правда, есть важная деталь: коэффициент преломления лучей по мере движения от красного цвета к фиолетовому будет монотонно меняться, соответственно будет монотонно меняться (точнее, уменьшаться) и угол интенсивного свечения для данного цвета. Для фиолетового цвета, второй границы спектра, этот угол примерно равен $41°$ (точнее, $40°\ 36'$).
Итак, лучи, падающие на верхнюю половину капли и отразившиеся внутри неё только один раз, порождают выходящие из капли разноцветные лучи, которые можно разделить на две группы. Во‐первых, из каждой маленькой капли выходит узкий пучок разбегающихся интенсивно окрашенных разноцветных лучей, составляющих с направлением падающих солнечных лучей углы от $41°$ (фиолетовый) до $42°$ (красный). Этот пучок порождается солнечными лучами, расстояние от которых до центра капли составляет примерно $0{,}86$ её радиуса. Во‐вторых, в диапазоне от $0°$ до $41°$ собираются лучи всех цветов и малой яркости, порождающие мягкий рассеянный свет от капли. Наконец, вне интервала углов $(0°, 42°)$ вообще нет выходящих из капли лучей рассматриваемого типа.
От рассмотрения оптических свойств капель вернёмся к задаче описания радуги. Продолжим работу в «естественной» вертикальной плоскости, в которой находятся наблюдатель, Солнце за его спиной и ось «Солнце — наблюдатель», параллельная солнечным лучам. Перед наблюдателем — вертикальный срез облака капель. Из каждой капли выходят яркие разноцветные лучи, по каждому направлению в диапазоне от $41°$ до $42°$ — только один. Значит, если в глаз наблюдателя попадает один из этих лучей, то остальные проходят мимо, а сама эта капля становится для наблюдателя ярко-одноцветной.
Такой яркий луч, пересекая две параллельные прямые солнечных лучей, проходящих через наблюдателя и каплю, образует с ними равные накрест лежащие углы. Например, каждая капля испускает красный луч под углом $42°$, поэтому наблюдатель увидит на небе ярко-красную точку тоже под углом $42°$ к оси «Солнце — наблюдатель». Можно показать, что для наблюдателя все капли в толще дождя, расположенные рядом с лучом $42°$, будут ярко-красными.
Наблюдателем все капли внутри угла $41°$—$\mkern1mu42°$ (в вертикальной плоскости) будут восприниматься как видимый объект — кусочек радуги, сияющей всеми цветами спектра от красного до фиолетового.
Вращением этого фрагмента радуги вокруг оси «Солнце — наблюдатель» можно получить полный портрет радуги (так как в каждой плоскости, проходящей через ось, процессы одинаковые). Радуга в небе как видимый объект для наблюдателя — круговая дуга «толщиной» около $1°$ и с центром на оси «Солнце — наблюдатель» (говорят, что центр радуги находится в противосолнечной точке).
Для каждого цвета спектра соответствующая окружность представляет все ярко-одноцветные точки, уходящие вдаль по образующим кругового конуса, ось которого — «Солнце — наблюдатель», вершина — наблюдатель, а полураствор (в зависимости от цвета) — от $41°$ (фиолетовый) до $42°$ (красный).
Высота радуги в небе зависит от положения Солнца. Например, если Солнце садится, то на коромысле качелей «Солнце — наблюдатель — центр радуги» будет подниматься противовес Солнца — центр радуги, а с ним и вся радуга. И наоборот: чем выше Солнце, тем ниже радуга, тем меньше её дуга. Самая большая радуга, почти половина окружности, — когда Солнце находится у линии горизонта. А вот с самолёта на фоне облаков можно увидеть радугу и в виде полной окружности.
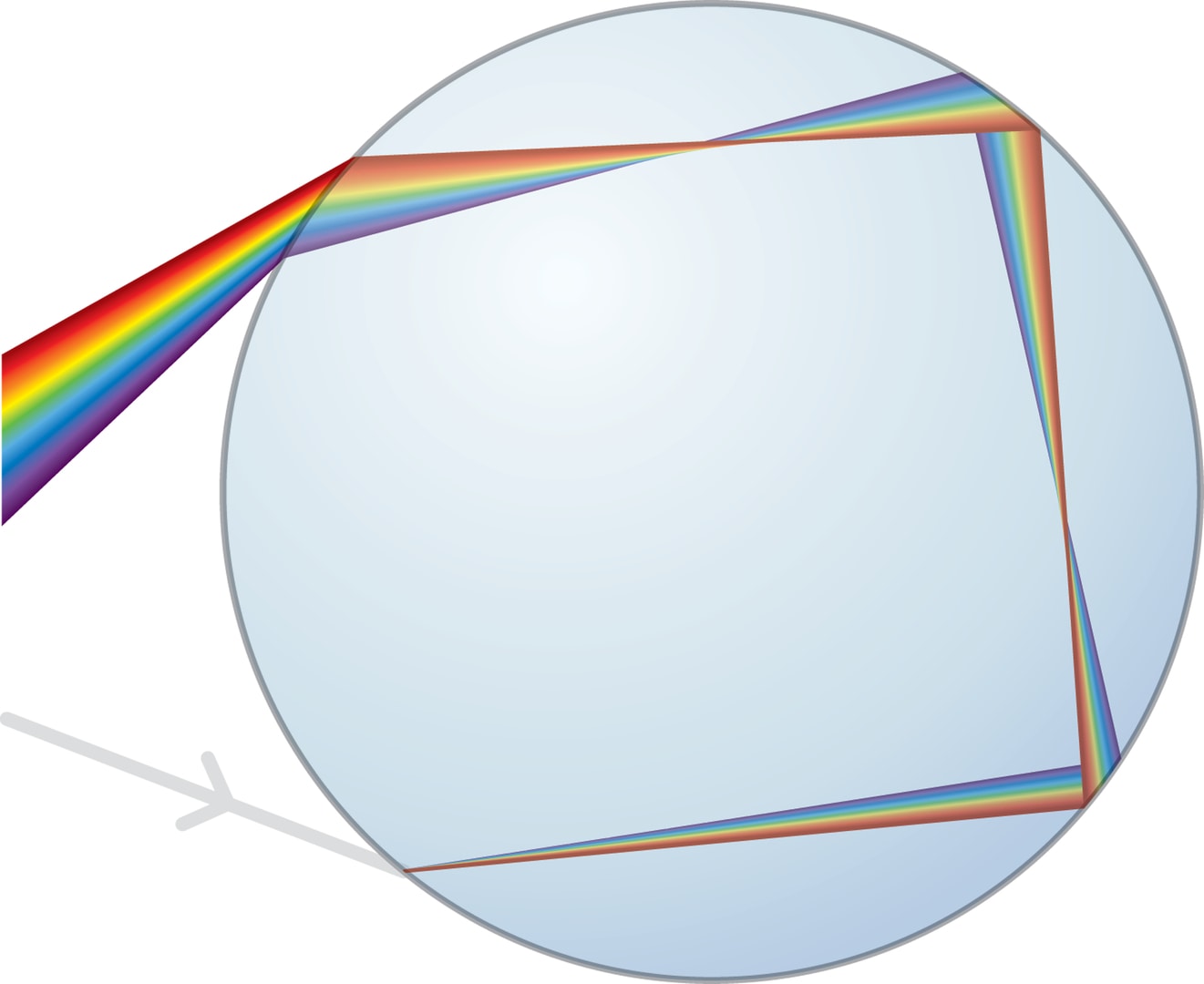
Иногда в небе видна и вторая радуга. В отличие от первой радуги, у формирующих вторую радугу солнечных лучей более сложный путь. В вертикальной плоскости лучи падают на нижнюю половину капли, преломляются, отражаются от стенок капли два раза, ещё раз преломляются и выходят наружу. Два внутренних отражения приводят к четырём изменениям в свойствах выходящего из капли пучка: угловой диапазон смещается в район $51°$—$52°$; он становится шире; интенсивность излучения снижается; порядок цветов меняется на противоположный.
Перечислим свойства второй радуги, сравнивая их со свойствами первой: в небе «висит» примерно на $10°$ выше первой, угловая толщина около $2°$, является менее яркой (иногда её просто не видно невооружённым глазом), порядок цветов в ней обратный — от фиолетового до красного (сверху вниз).
Если вам повезло и на небе видна двойная радуга, то станет заметным ещё одно оптическое явление: тёмная полоса между первой и второй радугами. Названная полосой Александра в честь описавшего её древнегреческого философа, эта область темнее, чем области ниже первой радуги и выше второй. Дело в том, что в области ниже первой радуги, от $0°$ до $41°$, наблюдатель видит мягкое свечение, вызванное рассеянием солнечных лучей (о котором уже говорилось). Аналогичная картина и выше второй радуги. А вот зона между радугами освещена только общим светом неба.
Рассмотренные радуги — первая и вторая — возникают в зависимости от числа внутренних отражений солнечных лучей в капле. Теоретически, формируются и радуги, порождённые большим числом отражений лучей в капле, но поскольку при каждом отражении энергия теряется, радуги высоких порядков — бледные, неяркие и заметить их трудно.
Рене Декарт был не только великим математиком и философом, но и естествоиспытателем, ставившим остроумные эксперименты, требовавшие изобретательности и упорства.
В знаменитом труде «Рассуждение о методе» Декарт сформулировал принципы научного исследования и применил их к изучению явлений природы, в частности радуги. Понимая, что элементы радуги возникают в каждой капле воды, Декарт, как он пишет, решил «создать очень большую каплю», для чего «наполнил водой большой стеклянный сосуд, вполне круглый и вполне прозрачный». Наблюдая с разных точек прохождение солнечных лучей через сосуд Декарт обнаружил, что под углом $42°$ к направлению падающих лучей капля-сосуд излучает ярко-красный свет, т. е. капля становится «фонариком», который в сторону источника света излучает красные лучи по образующим конуса с углом полураствора $42°$.
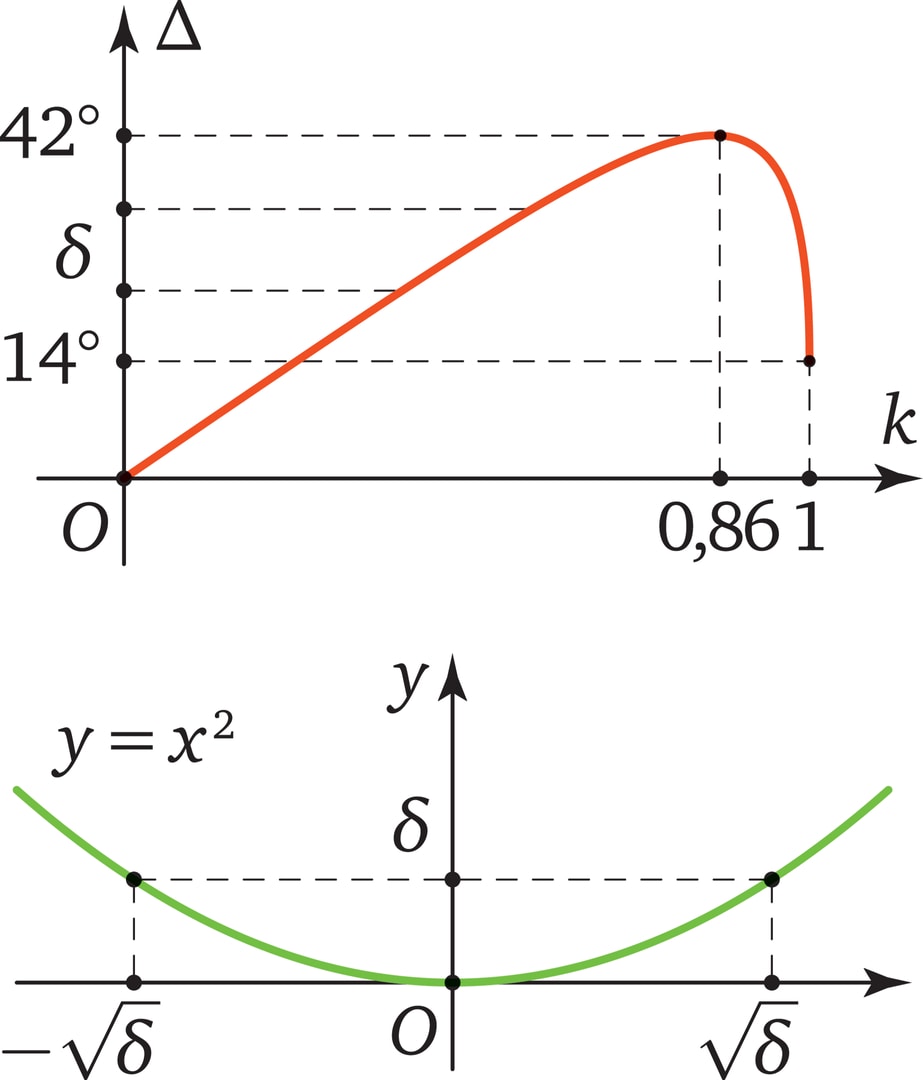
Обнаружив эффект экспериментально, Декарт объяснил его, опираясь на проделанные расчёты. Углы выхода лучей из капли он вычислил с помощью закона преломления. В силу симметрии движение солнечного луча (точнее, его монохромных составляющих) внутри капли зависит только от расстояния между падающим лучом и её центром. Технически удобно проводить анализ, используя параметр $k=\frac{\mathrm{расстояние}}{\mathrm{радиус}}$. Коэффициенты преломления монохромных лучей различны, поэтому выделим у каждого падающего луча одну компоненту, — например, красную.
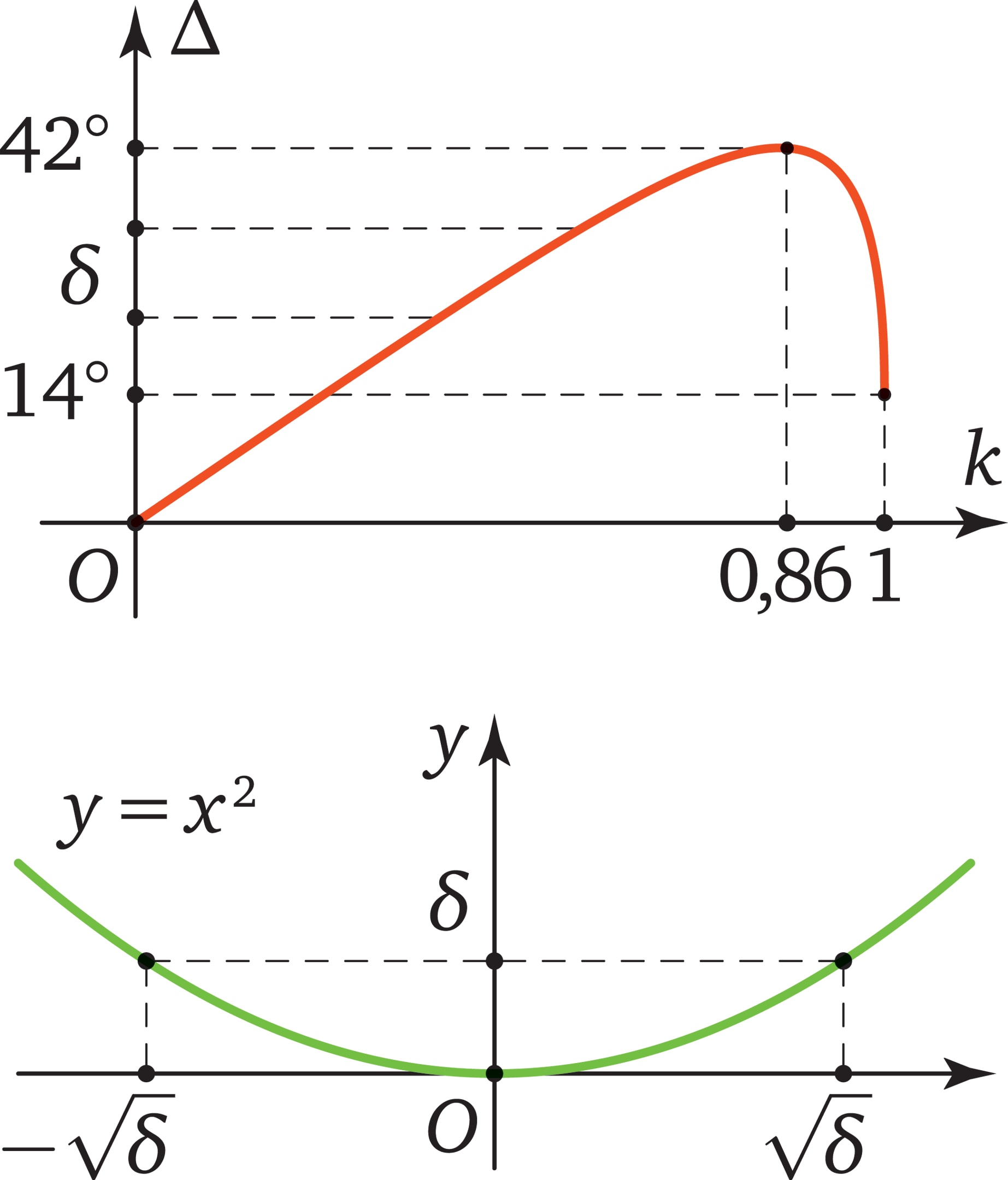
Сначала Декарт провёл расчёты для $k$ от 0 до 1 с шагом $0{,}1$. Затем, обнаружив, что наибольшие значения угла выхода получаются при $k=0{,}8$ и $k=0{,}9$, прошёл интервал $[0{,}8; 0{,}9]$ с шагом $0{,}01$. Результат оказался тот же, что и в эксперименте: наибольший угол — примерно $42°$, достигается это значение при $k=0{,}86$. Более точно, при увеличении $k$ от $0$ до $0{,}86$ угол возрастает от $0°$ до $42°$, а при дальнейшем увеличении $k$ от $0{,}86$ до 1 угол начинает уменьшаться.
На основе составленной им таблицы Декарт заключил, что «имеется гораздо больше» лучей в окрестности значения $42°$, чем при меньших значениях. А вне конуса (вершина — капля, ось — направление падающих лучей) полураствора $42°$ вообще нет выходящих из капли красных лучей.
Объясним почему выходящие из капли красные лучи группируются около экстремального угла $42°$ и, как следствие, почему столь велика энергия (яркость) этого пучка лучей.
Угол выхода луча в зависимости от параметра $k$ представлен на графике (здесь, как и в предыдущем комментарии, $k$ — это дробь, числителем которой является расстояние между падающим лучом и центром капли, а в знаменателе — её радиус).
Поток падающих лучей по параметру $k$ распределён равномерно, поэтому график «говорит», что на наклонных участках количество выходящих лучей, находящихся в каком‐то угловом интервале, пропорционально $\delta$ — его длине. Но в «шапочке» кривой, в окрестности максимального значения $\Delta_{\max}=42°$ соотношения другие. В окрестности точки экстремального значения функция замирает, её значения почти не меняются.
Приближённый вид «шапочки» — перевёрнутая парабола (знающие формулу Тейлора сразу это поймут). Для наглядности рассмотрим обычную параболу $y=x^2$.
В полосе $0<y<\delta$ лежат значения функции от аргумента $x\in (-\sqrt{\delta}; \sqrt{\delta}).$ Если $\delta$ много меньше, чем 1, то величина $\sqrt{\delta}$ значительно больше, чем $\delta$ (например: если $\delta=0{,}01$, то $\sqrt{\delta}=0{,}1$). Возвращаясь к «шапочке», получаем, что энергия данного пучка угловой ширины $\delta$ будет пропорциональна $\sqrt{\delta}$, а не $\delta$, как на наклонных участках. Эти лучи и создают ярко светящуюся точку — точку радуги.
Арнольд В. И. Математическое понимание природы. — М.: МЦНМО, 2010. — [Сюжет «Радуга»].
Панов А. Радуга Декарта—Ньютона—Юнга
Тарасов Л. В., Тарасова А. Н. Беседы о преломлении света. — М.: Наука, 1982. — (Библиотечка «Квант»; Вып. 18).
Нуссенцвейг Х. Теория радуги
Миннарт М. Свет и цвет в природе. — М.: ГИФМЛ, 1958.
Зверева С. В. В мире солнечного света. — Л.: Гидрометеоиздат, 1988.
Декарт Р. О радуге
Ньютон И. Оптика, или Трактат об отражениях, преломлениях, изгибаниях и цветах света. — 2‐е изд. — М.: ГИТТЛ, 1954.