Земля движется вокруг Солнца и одновременно вращается вокруг своей оси, наклонённой к плоскости орбиты. Смена времён года происходит из‐за этого наклона, а смена дня и ночи — следствие вращения Земли вокруг оси. Но наличие наклона оси в некоторых частях Земли разрушает привычное чередование дней и ночей. К полюсам примыкают шапочки, в которых наблюдаются полярные дни и полярные ночи — периоды длиной в несколько суток, когда Солнце не опускается за горизонт или не поднимается над горизонтом.
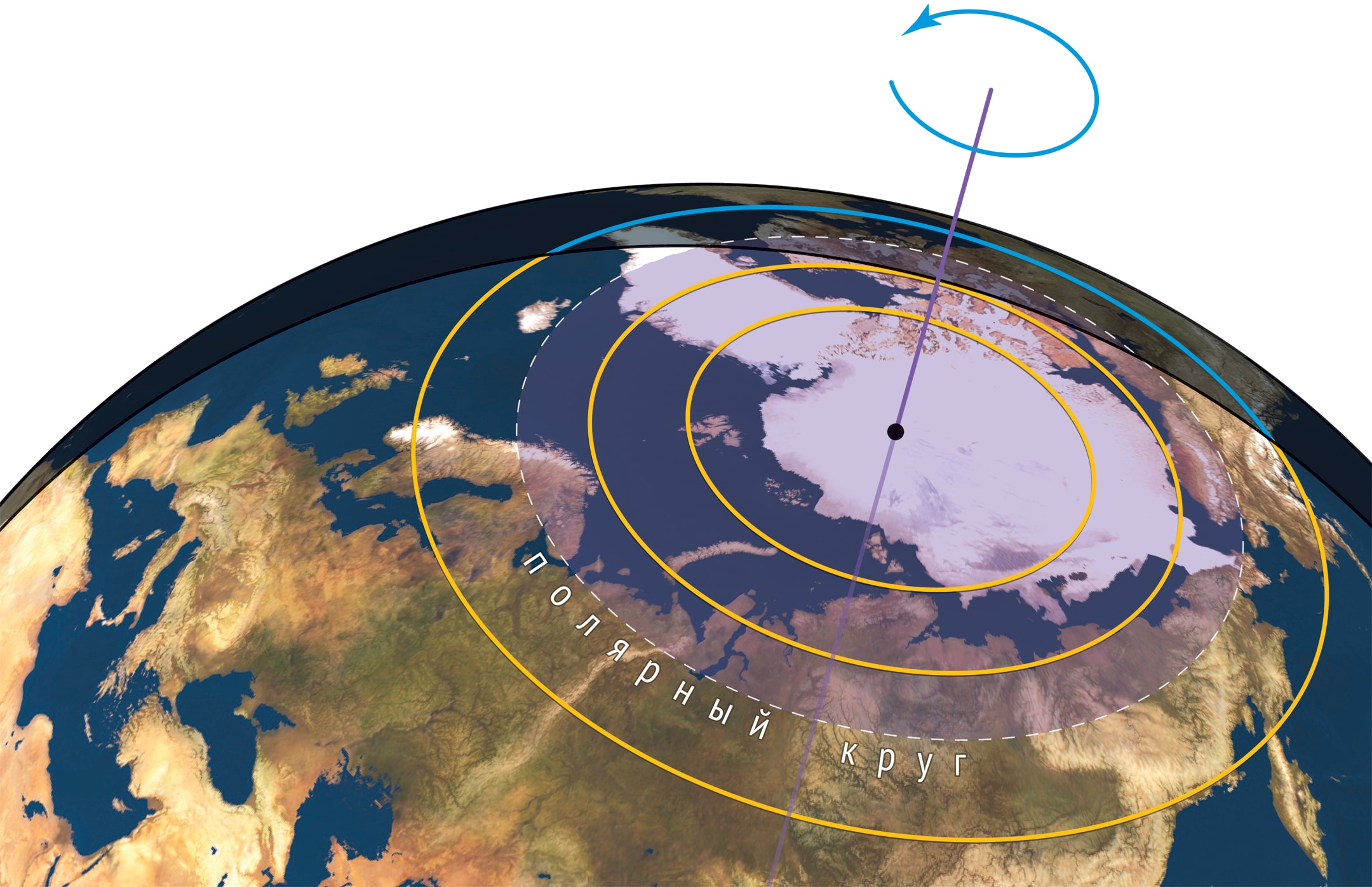
Чтобы понять происхождение полярных дней, посмотрим на Северное полушарие Земли в летние месяцы. Траектория любой точки при суточном вращении Земли будет окружностью, перпендикулярной оси. А если точка близка к Северному полюсу, то все точки этой окружности будут освещены, т. е. на достаточно высокой широте Солнце будет светить и день, и ночь.
Если окружность раздувать, то она коснётся терминатора — линии, разделяющей освещённую и неосвещённую полусферы. Название происходит от латинского terminus — граница, был в Древнем Риме и почитаемый бог границ и межевания Термин.
А для точек ниже этой окружности суточная траектория будет проходить, и по освещённой и по неосвещённой частям, т. е. смена дня и ночи вернётся.
Теперь можно сформулировать и конкретные вопросы. Например, в каких широтах наблюдается полярный день и сколько суток он длится? Но главная задача — определение длительности светового дня на данной широте в какой-то день года по его порядковому номеру. Решение задачи будет предъявлено, но сначала стоит описать движение Земли вокруг Солнца.
Анализируя годовое движение Земли по орбите, будем считать, что ось Земли остаётся параллельной самой себе и всё время направлена на «бесконечно далёкую» Полярную звезду — в наши дни это $α$ Малой Медведицы. Угол $\varepsilon$ между осью и нормалью к плоскости орбиты постоянен и равен $\varepsilon=23° 26'$.
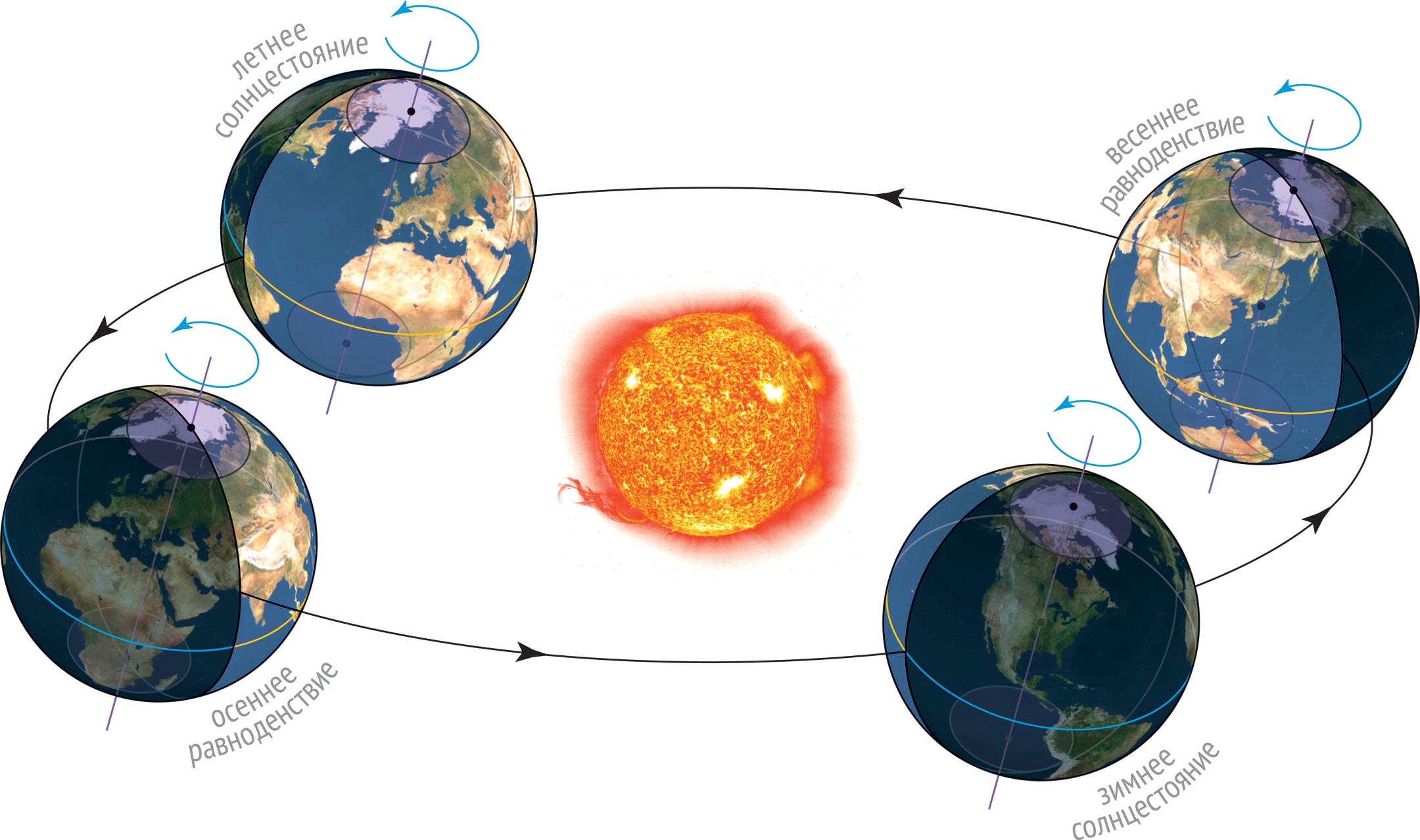
Это движение — периодическое, внутри периода выделяют четыре точки, которые делят год на четыре равные части.
Дни весеннего и осеннего равноденствия геометрически можно определить как моменты, когда ось вращения оказывается в плоскости терминатора. Из этого вытекает житейски привычное определение дней равноденствия: в любой точке Земли, на любой широте продолжительность дня равна продолжительности ночи.
Дни летнего и зимнего солнцестояния — моменты, когда ось Земли максимально отклонена от плоскости терминатора; продолжительность дней и ночей — экстремальна. Шапочки полярных дней и ночей становятся максимальными, их границы, широтные окружности, называются, соответственно, Северным и Южным полярным кругом. Из геометрического определения дней солнцестояния следует, что широта Северного (Южного) полярного круга равна $90°-\varepsilon=66° 34'$ ($-66° 34'$). За полярными кругами наблюдаются полярные дни и полярные ночи, а в полосе между Северным и Южным полярными кругами их не бывает.
Чтобы наглядно представить годовую динамику продолжительности светового дня и размеров шапочки полярного дня/ночи, выберем начальную точку отсчёта — день весеннего равноденствия и географическую область — Северное полушарие.
В течение трёх месяцев от весеннего равноденствия до летнего солнцестояния появляется и растёт шапочка полярного дня вокруг Северного полюса, в этой области день становится круглосуточным. Но и вне увеличивающейся шапочки дни становятся всё длиннее. Ось вращения Земли всё больше «смотрит» на Солнце, а землянам кажется, что оно с каждым днём поднимается всё выше над горизонтом. Летнее солнцестояние — время максимумов. Затем долгота дня и размер шапочки начинают уменьшаться, в день осеннего равноденствия день и ночь уравновешиваются, шапочка исчезает. В интервале между осенним и весенним равноденствиями история повторяется, только день и ночь меняются местами.
Динамика продолжительности дня/ночи и размеров полярных шапочек напоминает поведение синуса, но чтобы ассоциации превратить в инструменты, надо правильно выбрать аргументы. Орбита Земли — эллипс, но вытянутый совсем немного, так что в упрощённых расчётах можно заменить его окружностью. Положение точки на окружности задаётся углом в пределах от 0 до $2π$, в задаче о длительности дня естественный параметр — номер этого дня в календаре, от 1 до 365. Угловая метка дня с номером $n$ равна $2π\cdot\frac{n}{365}$, а с учётом сдвига точки отсчёта на день весеннего равноденствия (20 марта — 81‐й день в году) приходим к «правильному» аргументу: $2π\cdot\frac{n-81}{365}$.
В главной задаче определения длительности дня геометрически дело сводится к нахождению длин двух кусков широтной окружности, на которые она разбивается пересечением с терминатором. Технически решение задачи естественным образом приведёт к использованию тригонометрических функций. Вот итоговая формула для вычисления продолжительности светового дня в точке Земли на широте $s$ ($-90°<s<90°$) в день $n$ ($1\le n \le 365$):
$$ \frac{24}{π}\arccos(-{\tg s} \cdot \tg\arcsin(\sin\varepsilon \cdot \sin N)), \hbox{ где } N=\frac{2π}{365}\cdot(n-81). $$
В формуле аргументы тригонометрических функций представлены и в градусной мере ($s$ и $\varepsilon$), и в радианной ($N$, значения функций arccos и arcsin), результат измеряется в часах.
Чтобы увидеть эту формулу в действии, можно построить график зависимости продолжительности светового дня от номера дня в году, например, для Москвы ($55° 45'$ с. ш.). Каждый вертикальный отрезок (сутки) делится графиком на день (часть под графиком) и ночь (над графиком). В дни равноденствия эти части совпадают (день и ночь по 12 часов), в дни солнцестояния — максимум и минимум функции.
В точках ближе к экватору график становится приплюснутым, колебания длительности дня и ночи незначительны, а на самом экваторе — равноденствие круглый год (экватор всегда делится терминатором пополам).
Для всех широт между Северным и Южным полярными кругами формула для пары «день —ночь» работает «круглогодично». А в городах Заполярья, например, в Мурманске ($68° 58'$ с. ш.), в некоторые дни формула «не работает»: аргумент арккосинуса оказывается вне области определения (модуль больше 1). Это время полярного дня или полярной ночи.
В нашей идеализированной картине мира есть симметрия в парах «день—ночь», как «обычных», так и полярных. Дни и ночи симметрично устроены на широтах $\varphi$ и $-\varphi$. А полярные дни и ночи симметричны даже в двух смыслах. Скажем, в Мурманске длительность полярного дня и полярной ночи одинакова, по 30 дней. Кроме того, если в некоторый момент на широте $\varphi$ — свет полярного дня, то на $-\varphi$ будет тьма полярной ночи. Все эти факты можно «увидеть» геометрически, а можно извлечь и из свойств функций в основной формуле.
Приведённый анализ верен по сути, но не буквально. В рассмотренной простейшей модели не учитывались два существенных обстоятельства: Солнце — не точка; из‐за атмосферы Земли происходят рассеяние и преломление солнечного света. Реальный мир, оказывается, лучше и светлее, чем его модель.
День побеждает ночь. Световой день отнимает у ночи реальные минуты, даже в равноденствие; полярный день чуть длиннее, чем полярная ночь. С внешней стороны полярных кругов, например, в Санкт-Петербурге ($59° 57'$ с. ш.), в относительно небольшой полосе, наблюдаются белые ночи — ночи, которые выглядят как светлые сумерки.
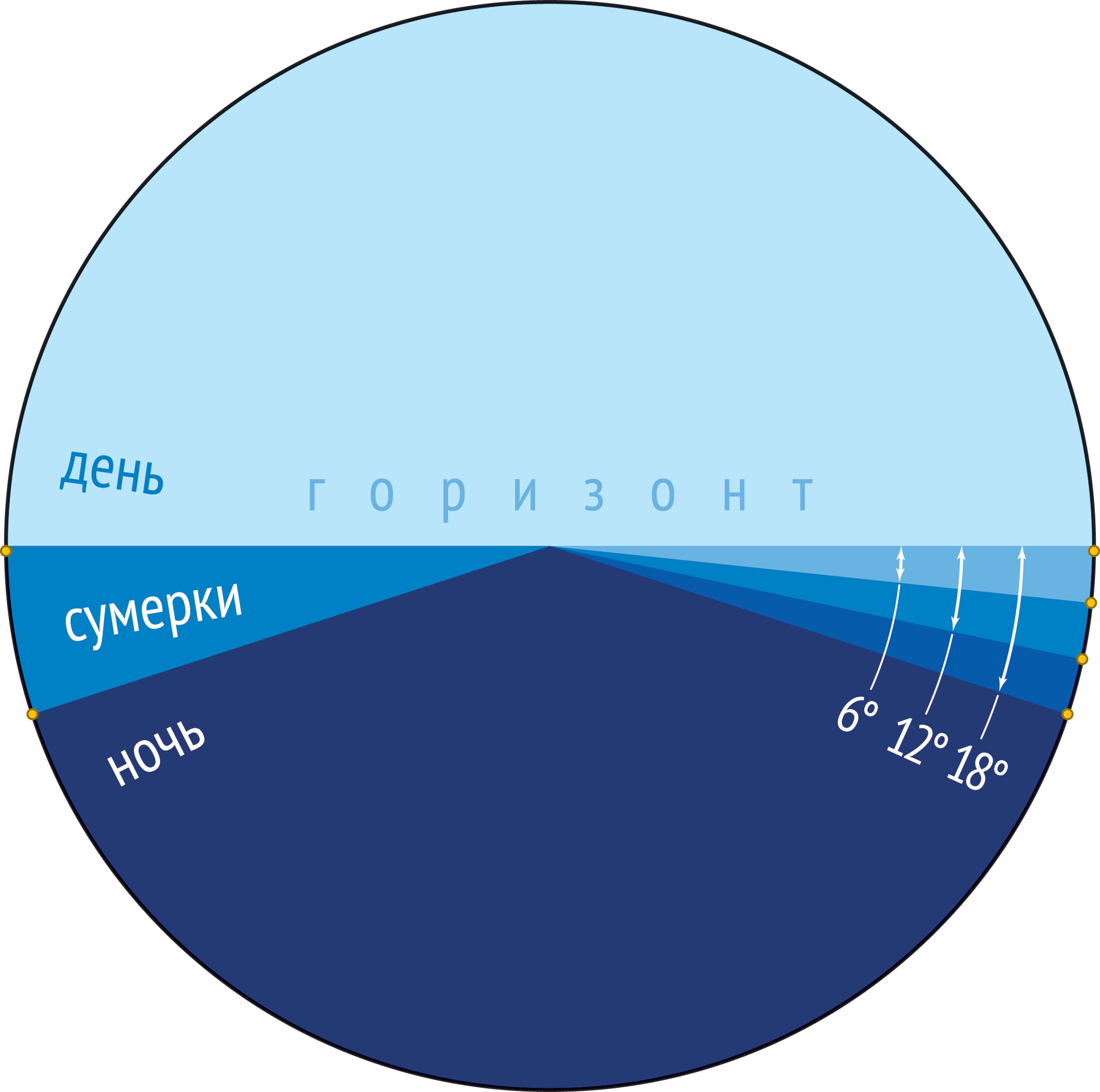
Заход Солнца не означает наступления темноты, да и светлеть начинает ещё до восхода Солнца. Этот период, «отнятый» у ночи, — сумерки. Главная причина возникновения сумерек — подсветка атмосферы находящимся за горизонтом Солнцем.
Для практических дел сумерки делят на три периода: гражданские; навигационные, или морские; астрономические. Границы зон формально определяются углом нахождения центра Солнца под горизонтом: до $6°$, от $6°$ до $12°$, от $12°$ до $18°$. Названия периодов соответствуют делам, которые ещё доступны в это время.
В гражданские сумерки можно выполнять на открытом воздухе любую работу; в конце этого периода включается искусственное освещение, гражданская жизнь замирает. В морские сумерки можно заниматься «без подсветки» некоторыми профессиональными делами; например, капитан плывущего вдоль берега корабля видит очертания предметов на берегу, но сами они обесцвечиваются. В астрономические сумерки только небо подсвечено, а затем исчезают и следы зари, на небе появляются звёзды — наступает рабочее время астрономов.
Белые ночи — это явление, когда вечерние гражданские сумерки переходят сразу в утренние, и это время суток — самое тёмное. Время белых ночей — летний период, в который светлое время круглосуточно, хотя Солнце и заходит за горизонт. В Северном полушарии это явление наблюдается летом в широтах несколько севернее $60°$ (эта граница определяется вычитанием из широты Северного полярного круга $66° 34'$ углового размера зоны гражданских сумерек, равного $6°$).
В нашей стране белые ночи ассоциируются с Санкт-Петербургом, хотя его широта — $59° 57'$ — немного меньше «необходимой». Следствие такого «недобора» — то, что даже в летнее солнцестояние в Петербурге белая ночь прерывается более тёмной частью почти на 2 часа.
На карте легко найти территории, крупные города, в которых можно наблюдать белые ночи, но не бывает полярного дня. Например, в России это города Надым ($65° 32'$), Печора ($65° 07'$), Архангельск ($64° 33'$), Якутск ($62° 02'$), Петрозаводск ($61° 48'$).
График зависимости длины светового дня от номера дня в году (скажем, для Москвы) подсказывает, что вблизи дней солнцестояния длительность дня меняется мало, почти застывает. Математически это объясняется тем, что в точке максимума или минимума производная функции — скорость её изменения — равна нулю, а в окрестности такой точки — мала (см. комментарий к статье «Радуга»). А вот весной и осенью, вблизи дней равноденствия, изменения длительности дня наибольшие.