Многие растения, встречающиеся в природе, изумляют сочетанием красоты, совершенства, оптимальности.
Одна из природных загадок, известная со времён Леонардо да Винчи, но до сих пор необъяснённая, носит название «филлотаксис» (название составлено из двух слов древнегреческого языка и буквально означает «расположение листьев»). Загадочным является наблюдаемое в мире растений геометрически правильное расположение листьев, лепестков, семян, характеристики которого подчиняются закономерностям арифметическим.
Причиной появления тонких математических закономерностей интересуются естествоиспытатели, от ботаников до физиков, гипотез множество, а нерешённый вопрос один: что оптимизируют растения, выстраивая элементы по правилам филлотаксиса? Признанного решения пока нет. Несмотря на это, убедиться в реальности математической составляющей филлотаксиса может каждый читатель.
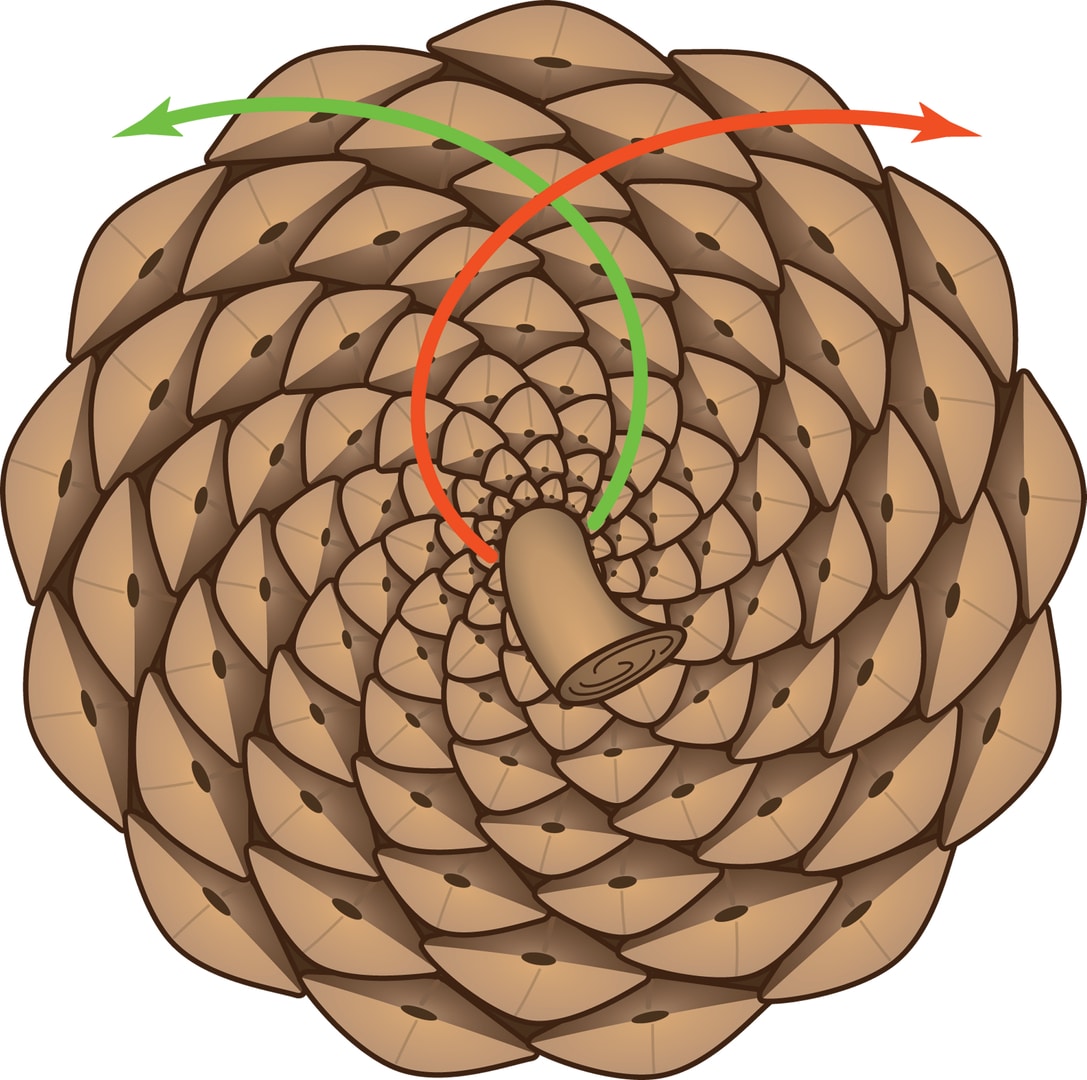
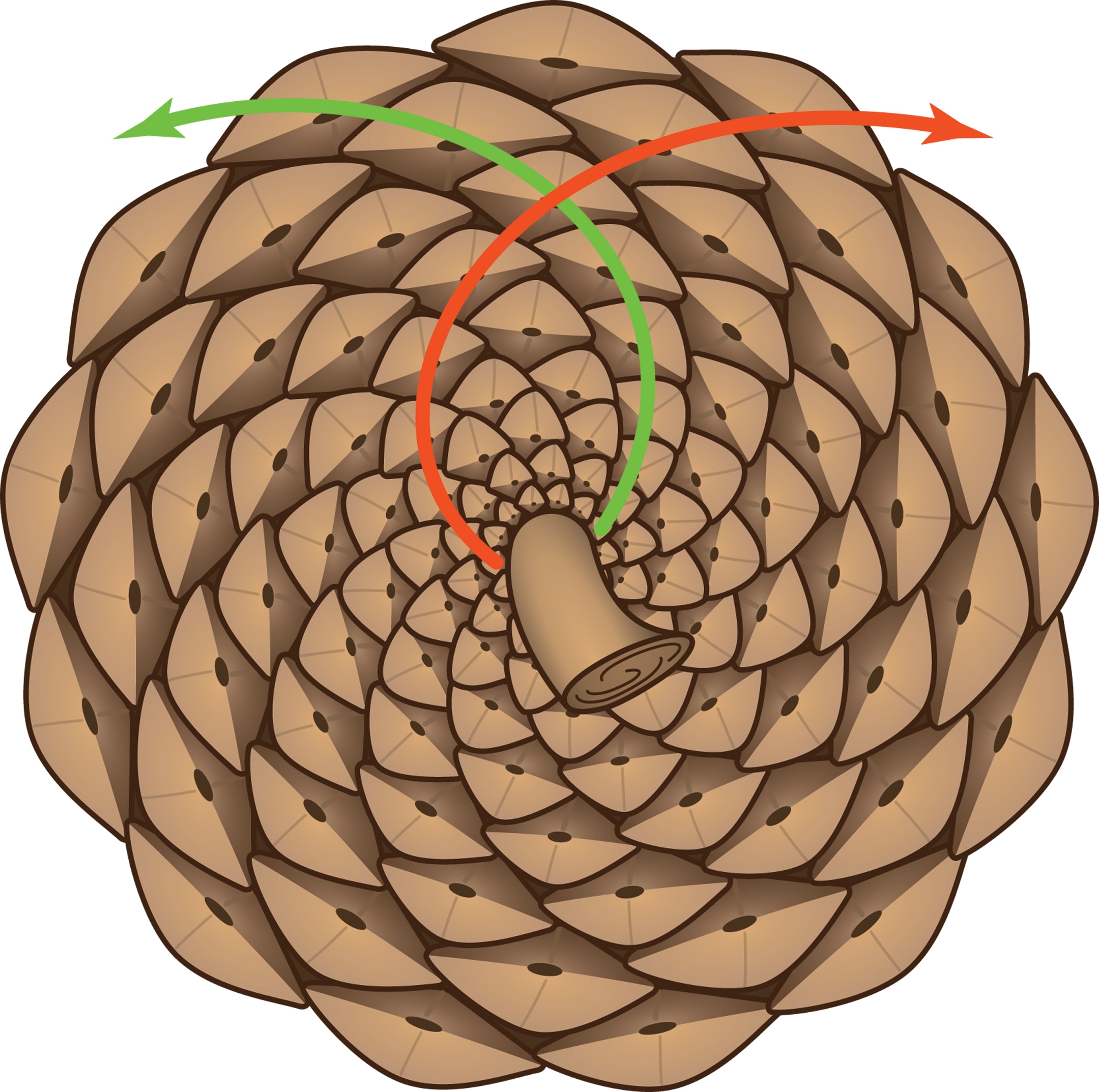
Возьмите еловую или сосновую шишку, ананас или диск подсолнуха. Сразу видно, что чешуйки в ананасе и шишке, семена в подсолнухе образуют регулярную структуру. Можно заметить и наличие на поверхностях спиралей двух типов — правых и левых. Если сосчитать количество однотипных спиралей, то с большой вероятностью вы получите одну из пар $(5, 8)$, $(8, 13)$, $(13, 21)$, $(21, 34)$, образованных двумя соседними числами Фибоначчи.
Последовательность чисел Фибоначчи $ \{1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …\} $ задаётся соотношением $F_n=F_{n-1}+F_{n-2}$ и парой начальных чисел $F_0=1$, $F_1=1$.
А теперь оторвитесь от книги и отправляйтесь в парк или в лес. Ищите, находите, рассматривайте и изучайте удивительные математические закономерности в мире растений.
Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — [Глава 11 «Золотое сечение и филлотаксис», стр. 236—252].
Воробьёв Н. Н. Числа Фибоначчи. — 4‐е изд., доп. — М.: Наука, 1978. — (Популярные лекции по математике; Вып. 6).
Грэхем Р., Кнут Д., Паташник О. Конкретная математика: Основание информатики. — М.: Мир, 1998. — [2‐e изд.: М.: Мир, Бином, 2009]. — [§ 6.6 «Числа Фибоначчи»]
Петухов С. В. Биомеханика, бионика и симметрия. — М.: Наука, 1981.