Представление о том, что ваш GPS- или ГЛОНАСС-приёмник получает ваши же координаты от находящихся на орбите спутников, — ошибочно. Во‐первых, спутники их просто не знают, во‐вторых, свои сообщения спутники не персонифицируют и отправляют «в пространство», сразу всем, а не только вашему приёмнику. Как же тогда навигатор определяет ваши координаты?
В спутниковой навигационной системе можно выделить два основных сегмента: космический и управленческий. Космический сегмент — созвездие спутников, равномерно расположенных вокруг Земли. Управленческий сегмент, находящийся на Земле, обеспечивает, в частности, синхронизацию на всех спутниках «общесистемного» времени и использование единой системы координат.
Каждый спутник постоянно передаёт навигационные сообщения, содержащие, в частности, координаты спутника в момент отправки сообщения и время отправки.
Приёмник, получивший такое сообщение, может рассчитать расстояние до спутника: $d=(t^{\mathrm{(пр)}}-t^{\mathrm{(отпр)}})c$.
В этой формуле время прохождения сигнала (от времени отправки $t^{\mathrm{(отпр)}}$ до времени приёма $t^{\mathrm{(пр)}}$) умножается на скорость распространения радиосигнала, т. е. скорость света $c$.
С другой стороны, если в прямоугольной декартовой системе координат ваши координаты равны $(x;y;z)$, а координаты спутника в момент отправки сообщения были равны $(x_1;y_1;z_1)$, то квадрат расстояния $d_1$ равен $(x-x_1)^2+(y-y_1)^2+(z-z_1)^2$.
Если приёмник одновременно получит навигационные сообщения ещё от двух спутников, то сможет найти ваши координаты $(x;y;z)$, решив систему из трёх уравнений $$ \begin{cases}(x-x_1)^2+(y-y_1)^2+(z-z_1)^2=d_1^2, \\ (x-x_2)^2+(y-y_2)^2+(z-z_2)^2=d_2^2, \\ (x-x_3)^2+(y-y_3)^2+(z-z_3)^2=d_3^2, \end{cases}$$
где $(x_i;y_i;z_i)$ — координаты $i$‐го спутника, а $d_i$ — расстояние до него.
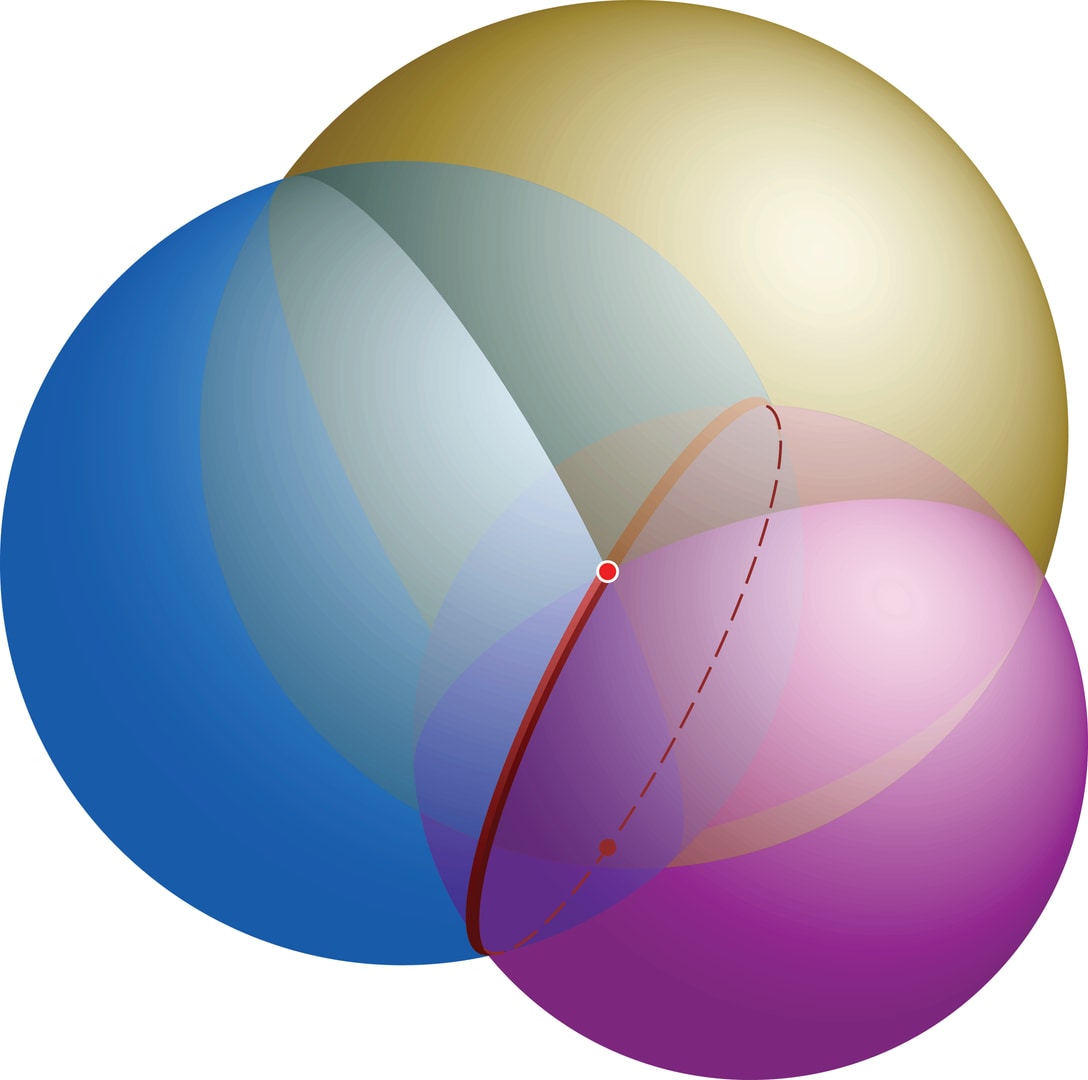
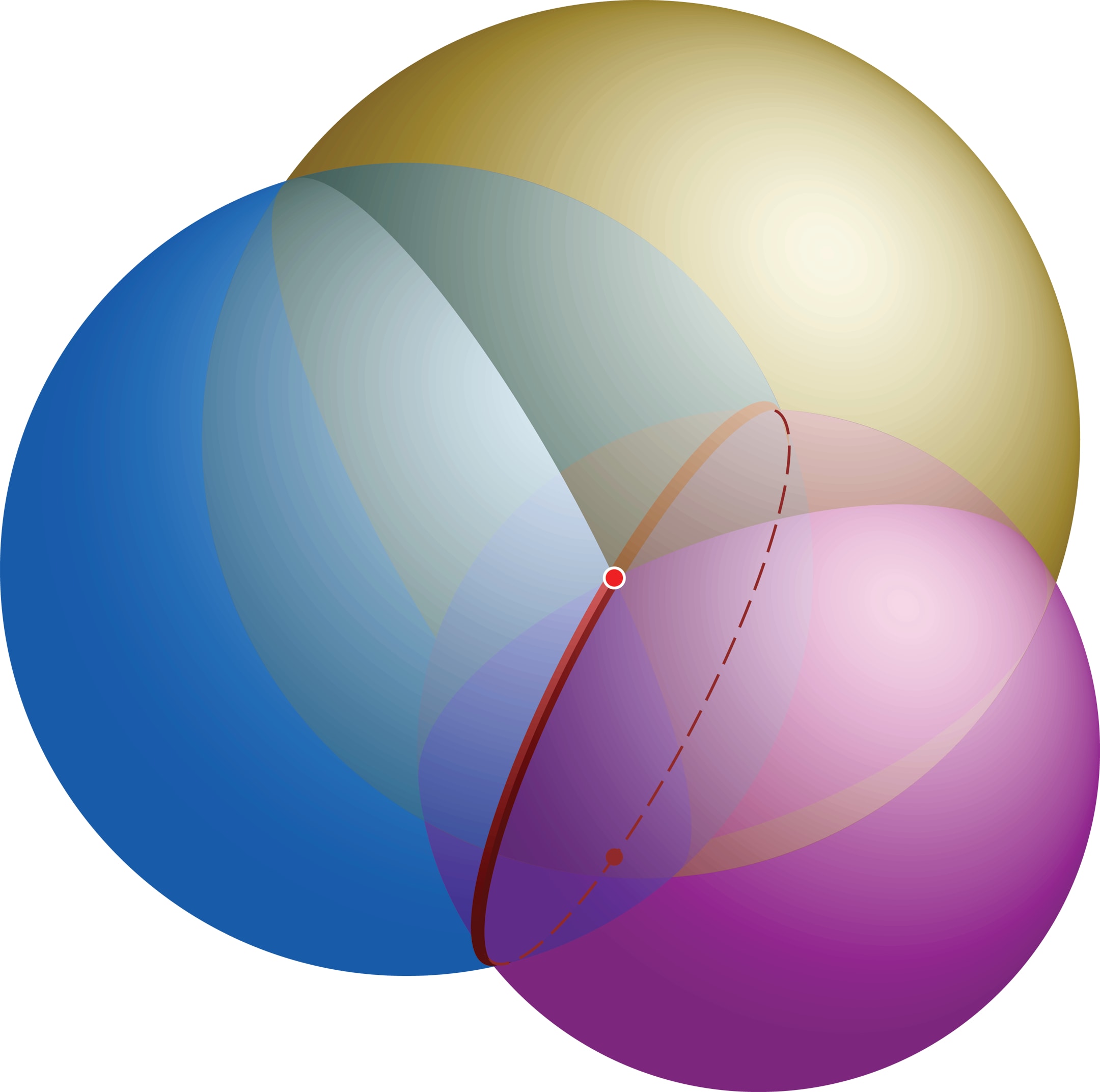
Геометрическая интерпретация этой системы такова. Сообщение от одного спутника выделяет часть пространства, в которой вы находитесь, — сферу, определяемую её центром-спутником и радиусом. Информация от второго спутника — ещё одна сфера. Пересечение этих двух сфер, вообще говоря, — окружность. Сообщение от третьего спутника добавляет ещё одно ограничение — ещё одну сферу — и уже однозначно определяет ваши координаты. То, что все три сферы имеют общую точку, следует из самого составления системы. Из двух «формальных» решений (пересечение окружности и третьей сферы) одно — неправдоподобно, второе — ваши координаты.
Описанная схема спутниковой навигационной системы — упрощённая, реальность заставляет использовать более сложную модель. Например, рассмотренная схема очень чувствительна к погрешностям, одна из главных проблем — влияние точности хода часов навигатора, который не имеет возможности связываться с наземными станциями навигационной системы для корректировки времени. Представьте что часы отстали от общесистемного времени на $0,001$ с. Скорость света равна $с=300 000$ км/с, таким образом, в определении расстояний до спутников (радиусов сфер) получится ошибка в 300 км! Выписанная система, если и будет иметь решение, то не относящееся к вашему местоположению…
К счастью, подобная проблема преодолима, причём даже в том случае, когда точность хода часов нам неизвестна. Допустим, что часы приёмника отстают от общесистемного времени на (неизвестную нам) величину $\delta$, и их показания в момент получения сообщения — $t^{\mathrm{(пр)}}$. Навигатор будет «считать», что расстояние до спутника равно $d=(t^{\mathrm{(пр)}}-t^{\mathrm{(отпр)}})c$, что меньше истинного расстояния $d+\delta c$.
Чтобы найти координаты $(x;y;z)$ и новую неизвестную $r=\delta c$, необходимо ещё одно уравнение, оно появится, если есть данные от четырёх спутников:
$$ \begin{cases}(x-x_1)^2+(y-y_1)^2+(z-z_1)^2=(d_1+r)^2,\\ (x-x_2)^2+(y-y_2)^2+(z-z_2)^2=(d_2+r)^2,\\ (x-x_3)^2+(y-y_3)^2+(z-z_3)^2=(d_3+r)^2,\\ (x-x_4)^2+(y-y_4)^2+(z-z_4)^2=(d_4+r)^2. \end{cases}$$
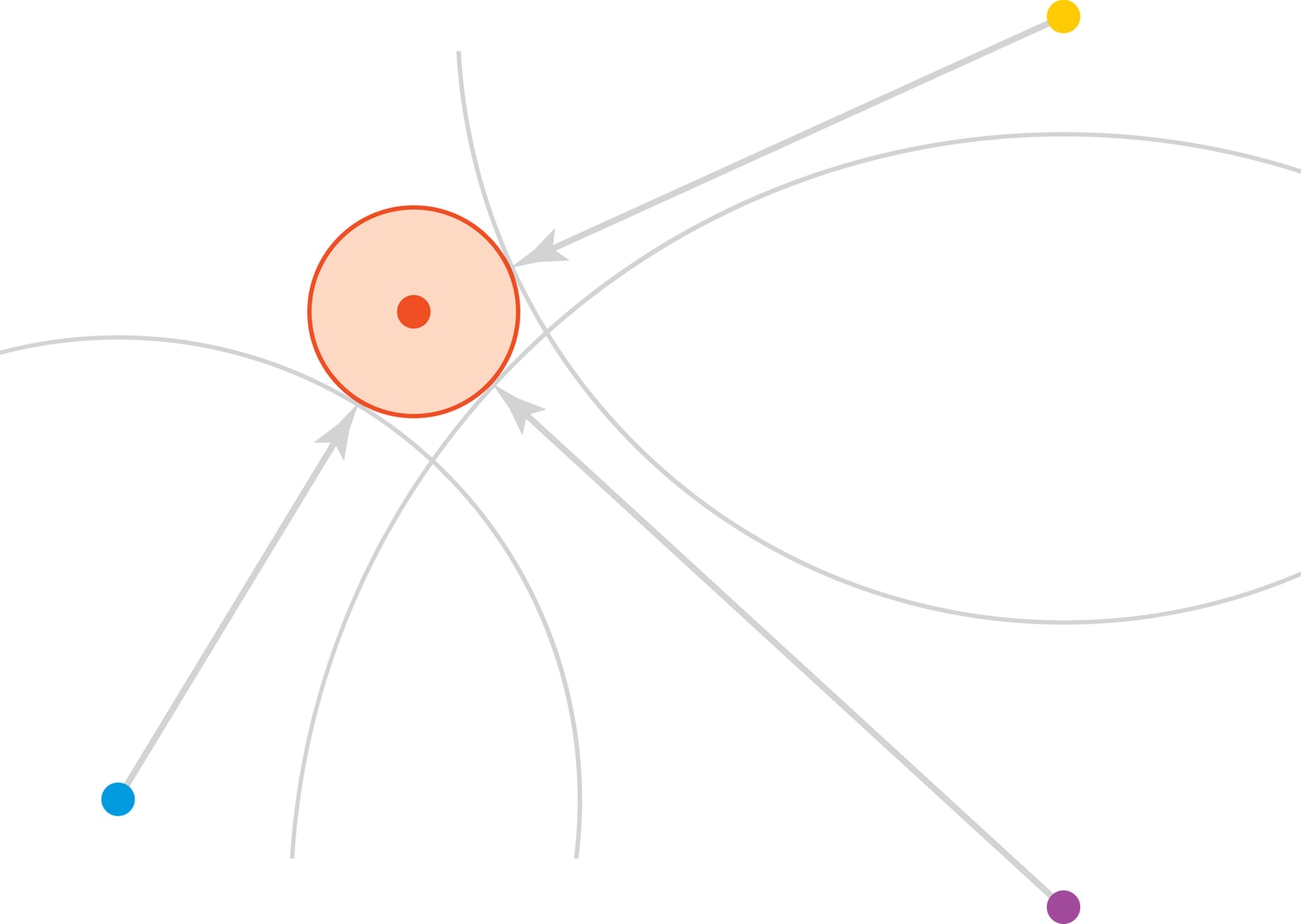
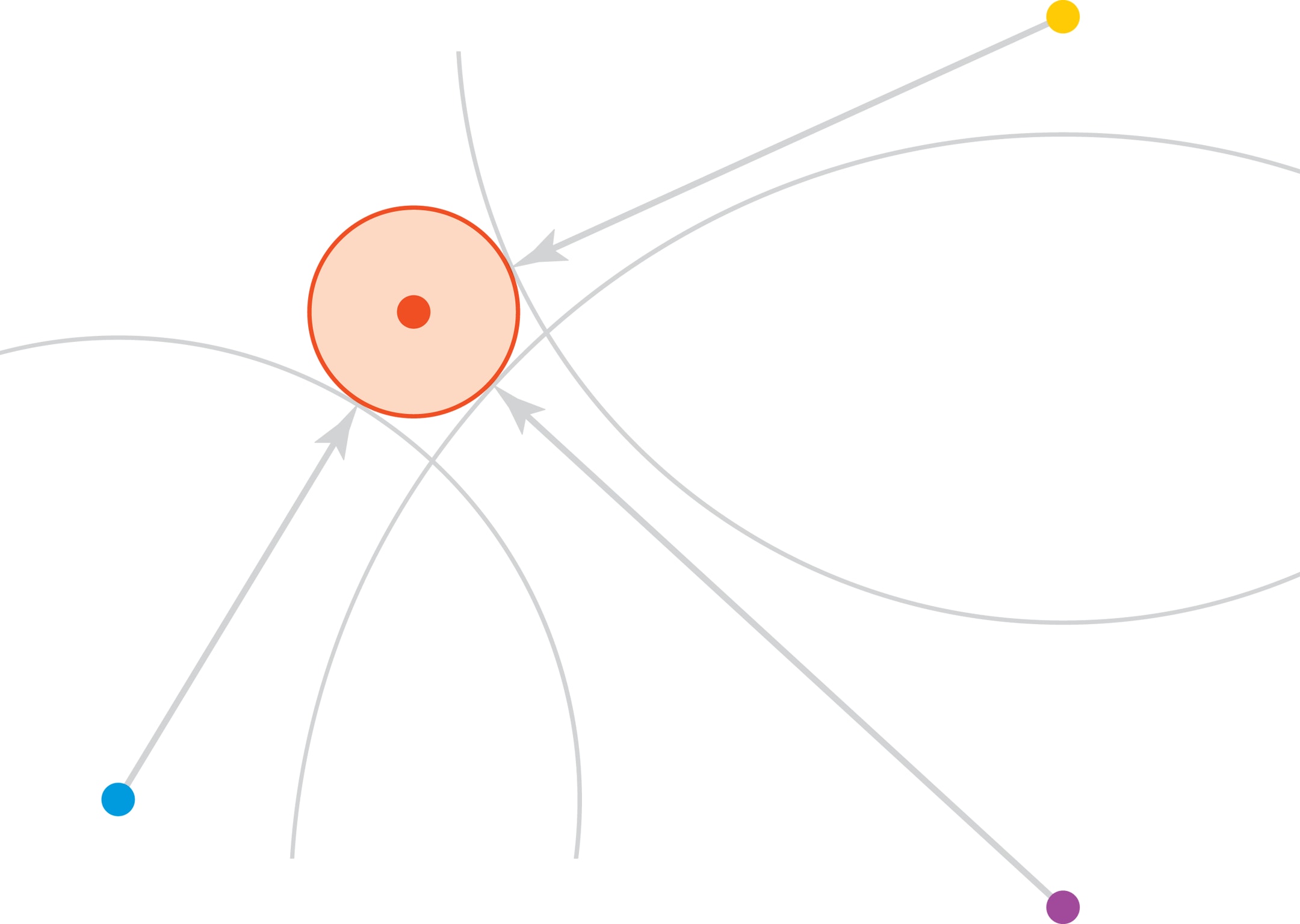
Геометрическая интерпретация решения задачи такова. Приёмник является центром сферы радиуса $r$, которая внешним образом (так как часы отставали) касается четырёх сфер радиусов $d_i$, центры которых — спутники. Такая сфера существует, а её центр — ваше местоположение. (На рисунке изображён двумерный вариант этой задачи: окружность радиуса $r$ внешним образом касается трёх окружностей.)
Вычислив координаты по этой системе, навигатор в качестве дополнительного «бонуса» получает значение общесистемного времени, корректирует свои часы и сообщает вам точное время!