Карты, схемы, путеводители обычно печатаются на больших прямоугольных листах бумаги. Для хранения и переноски эти листы складывают в несколько раз. Самый распространённый тип складывания — прямоугольный: лист разбивается на прямоугольники и складывается по линиям разбиения так, чтобы в сложенном виде у карты не было сгибов большой кратности (как у толстой пачки купюр, согнутой пополам).
При разворачивании карты или схемы проблем нет, но когда вы начинаете складывать карту, часто на каком‐то этапе оказывается, что её придётся перегибать в направлении, противоположном тому, что сохранил в своей «памяти» лист.
А можно ли придумать такое разбиение листа карты и такой способ складывания, чтобы:
1) развёрнутая карта складывалась бы «сама» и не было необходимости запоминать порядок складывания;
2) у листа карты в сложенном виде не было сгибов большой кратности.
Сформулированную задачу можно решить, используя приёмы, разработанные японскими мастерами оригами.
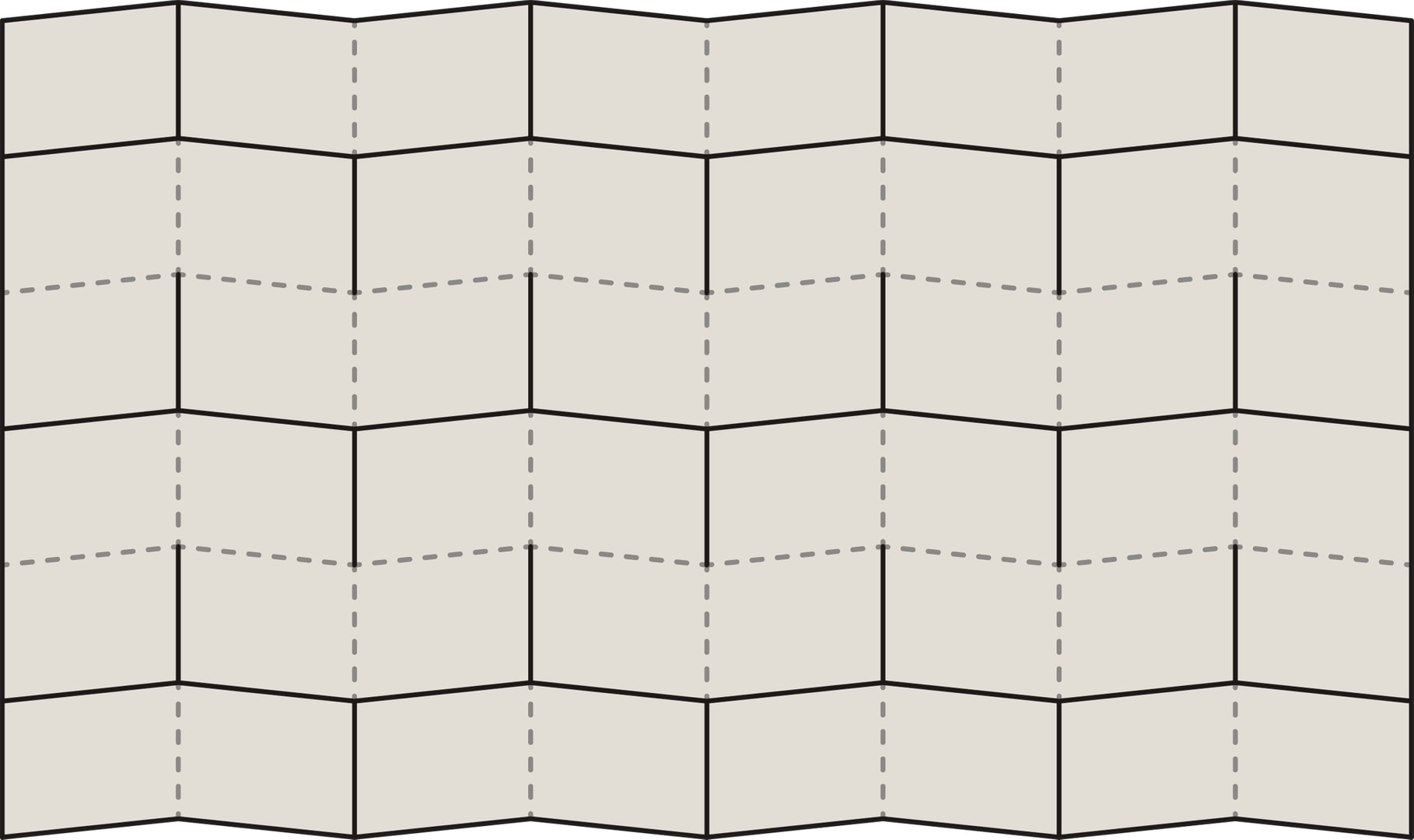
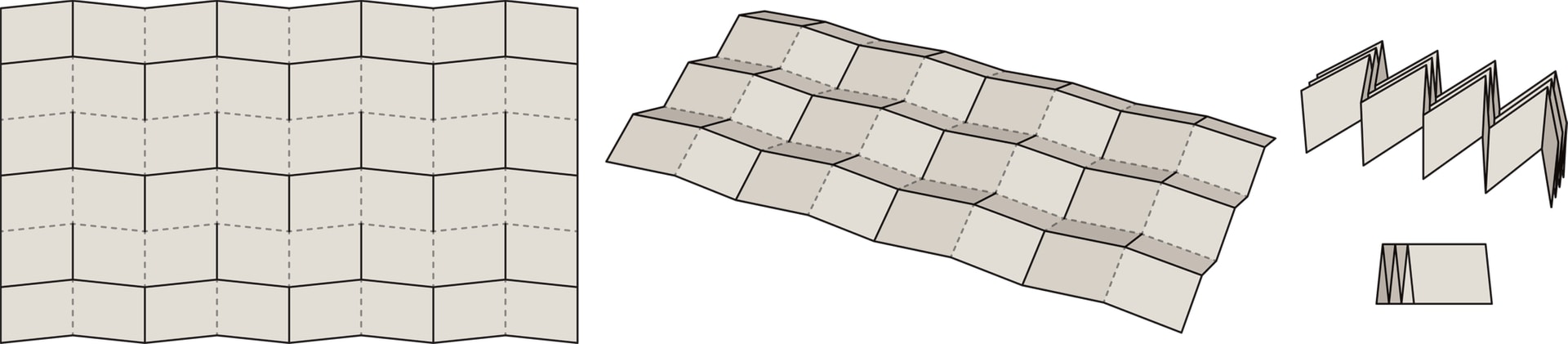
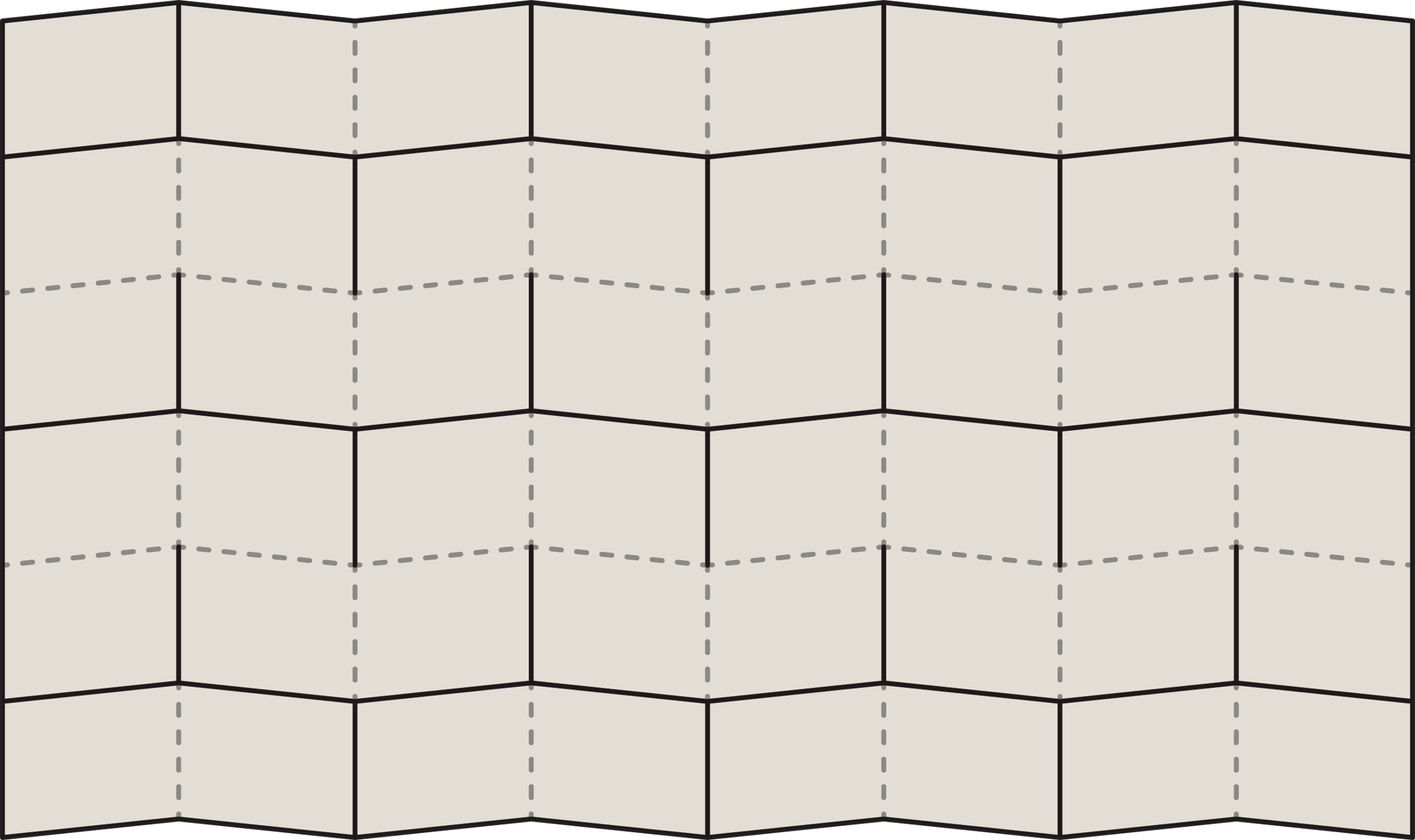
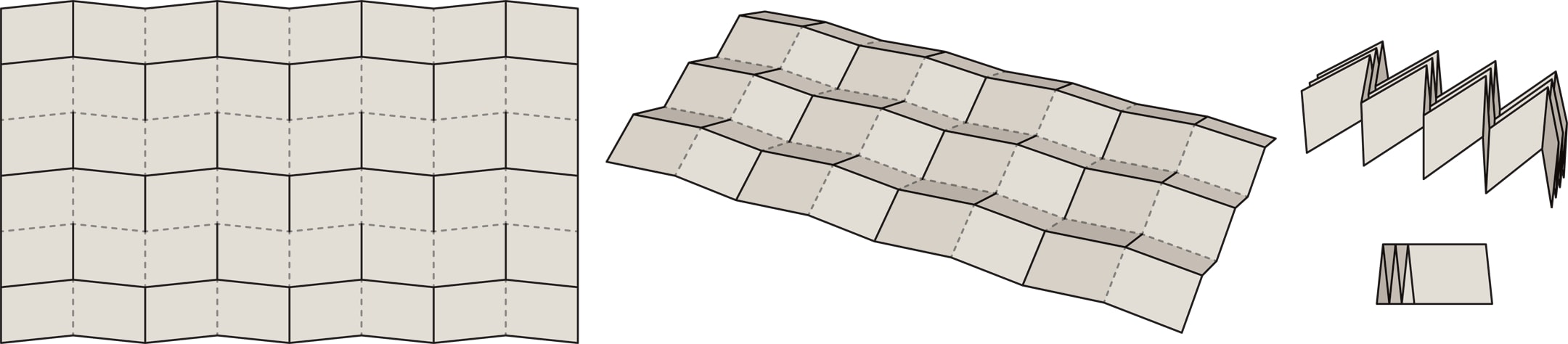
Лист карты разбивается на полосы, состоящие из параллелограммов. Если начать складывать такой лист «гармошкой» по вертикали, конструкция автоматически начнёт складываться и по горизонтали. Форма возникшей складчатой поверхности в каждый момент складывания однозначно определяется одним параметром — расстоянием между диагонально противоположными углами карты.
Приведённая конструкция замечательна ещё и тем, что параллелограммы могут быть жёсткими. Это открывает новые возможности для приложений. Например, так устроены солнечные батареи некоторых космических аппаратов.