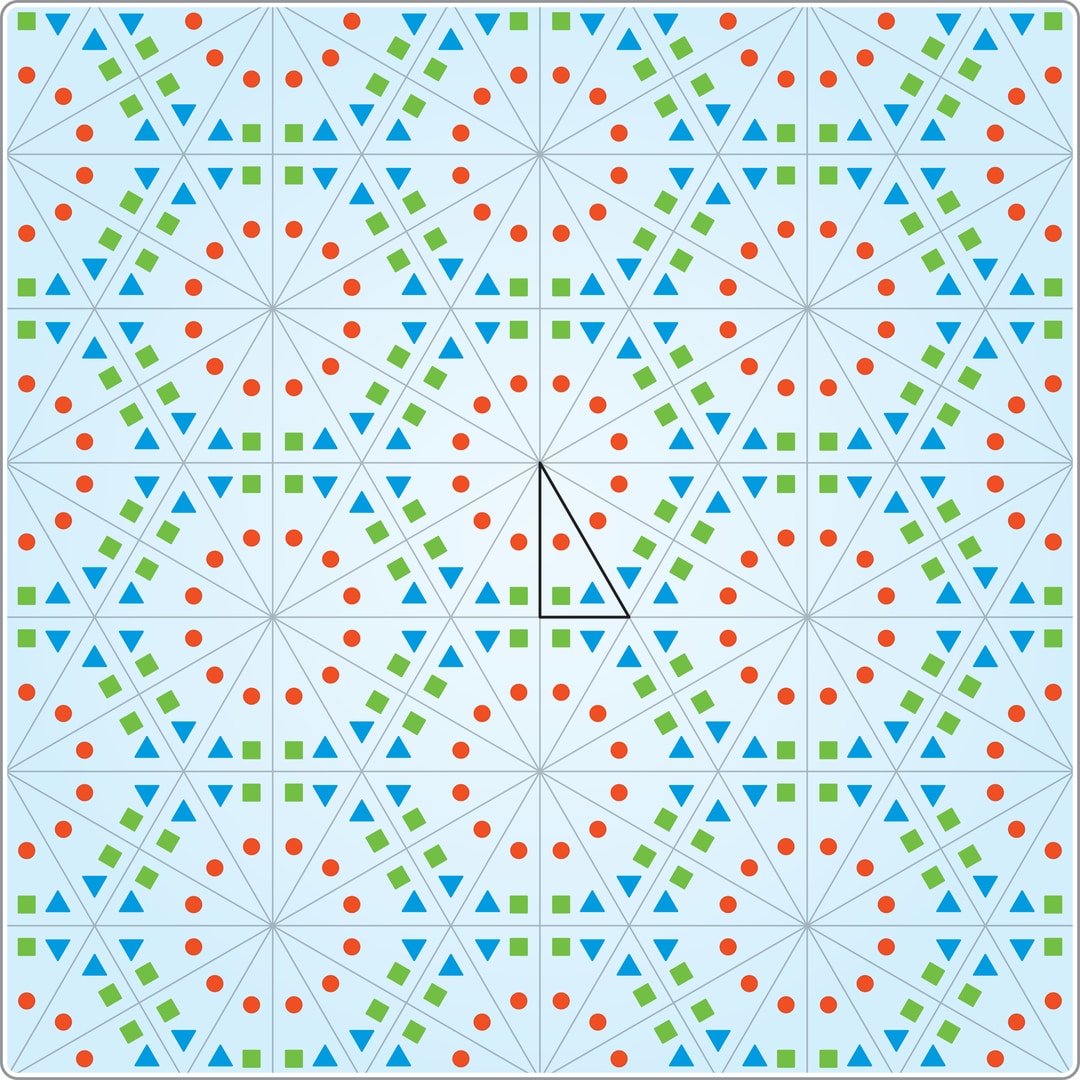
Калейдоскоп был придуман в начале XIX века. Его название происходит от древнегреческих слов καλός — красивый, εἶδος — вид, σκοπέω — наблюдаю. Это оптическое устройство, состоящее из трёх зеркал прямоугольной формы, сложенных в виде призмы («трубки») с треугольным сечением.
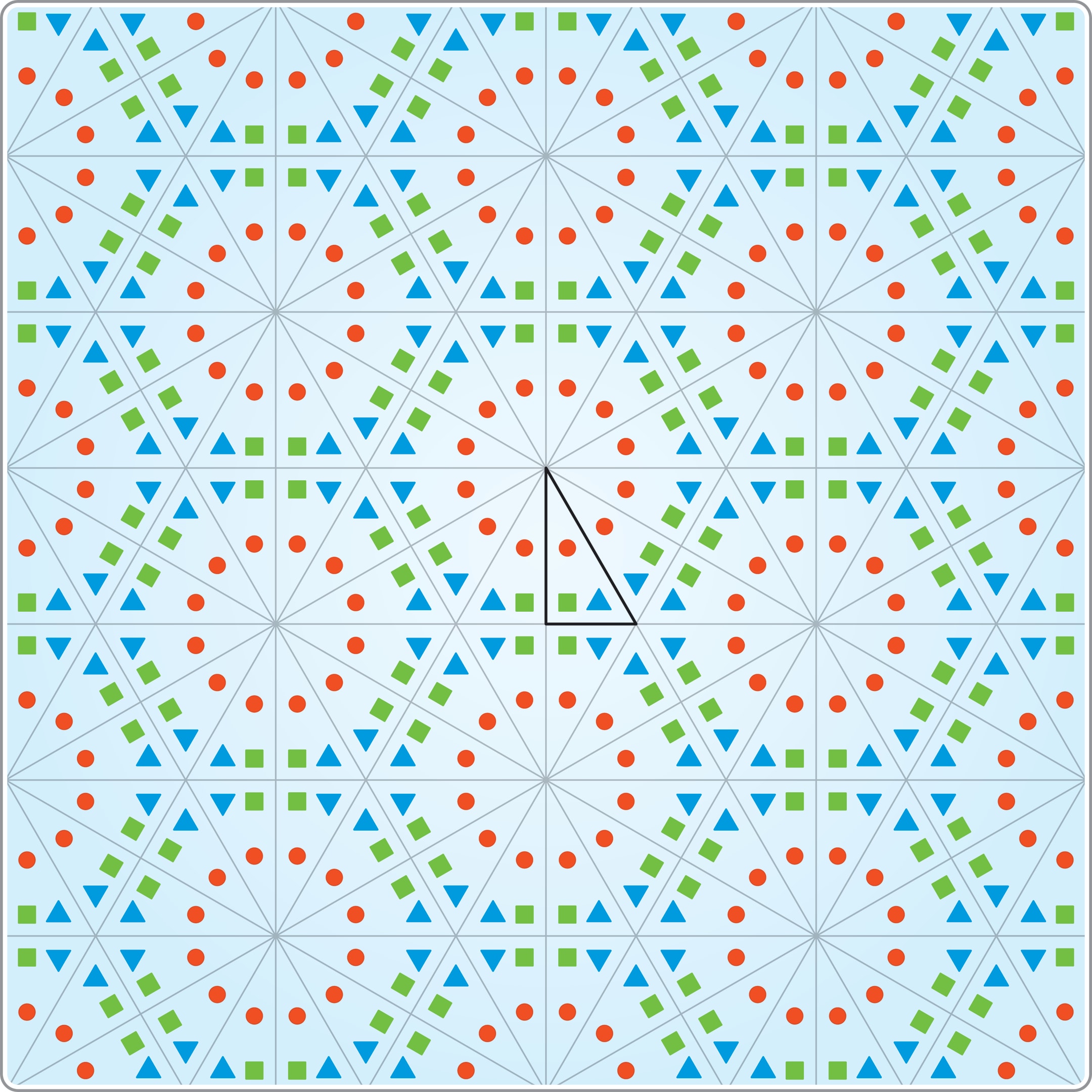
В одном из оснований призмы — двойное стеклянное дно, между стёклами насыпаны мелкие разноцветные предметы. В противоположном основании призмы — окуляр. При фиксированном положении калейдоскопа из предметов складывается картинка в «основном» треугольнике. Она многократно отражается в стенках-зеркалах, и наблюдатель через окуляр видит симметричный разноцветный узор.
При повороте калейдоскопа предметы пересыпаются, возникает новый, но тоже симметричный узор. Чтобы обеспечить симметрию узора и его «устойчивость» — лишь в этом случае устройство называют калейдоскопом, — для построения призмы подходят только три вида треугольников.
В самом распространённом типе калейдоскопов треугольник в сечении призмы равносторонний, у которого углы равны $60°$. Этот вариант удобен и с производственной точки зрения — все зеркала одинаковые.
Два других варианта — прямоугольные треугольники с углами $90°$—$45°$—$45°$ и $90°$—$60°$—$30°$.
Если рассматривать призмы не только с треугольным основанием, то калейдоскоп можно построить и на основе прямоугольника.
Чтобы понять, почему для изготовления калейдоскопа «на треугольниках» подходят только перечисленные варианты, вспомним, как формируется отражение в зеркале.
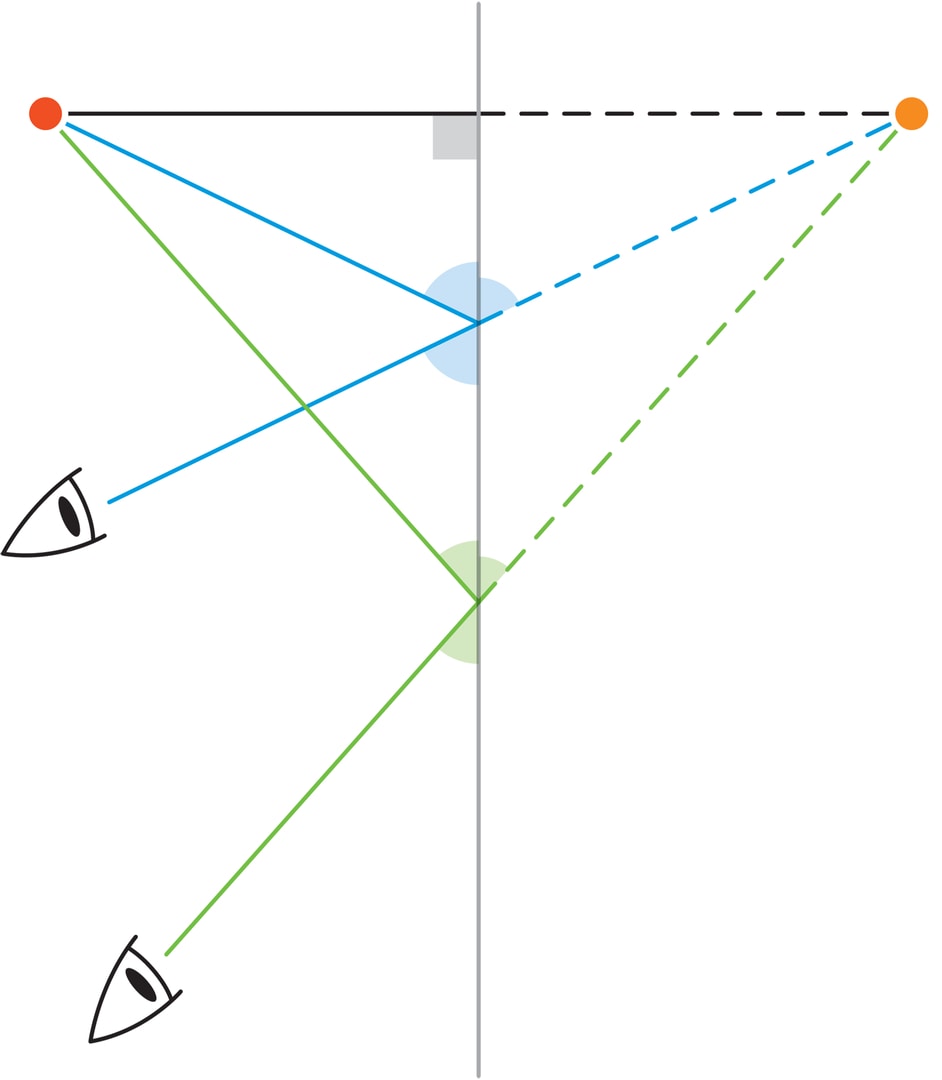
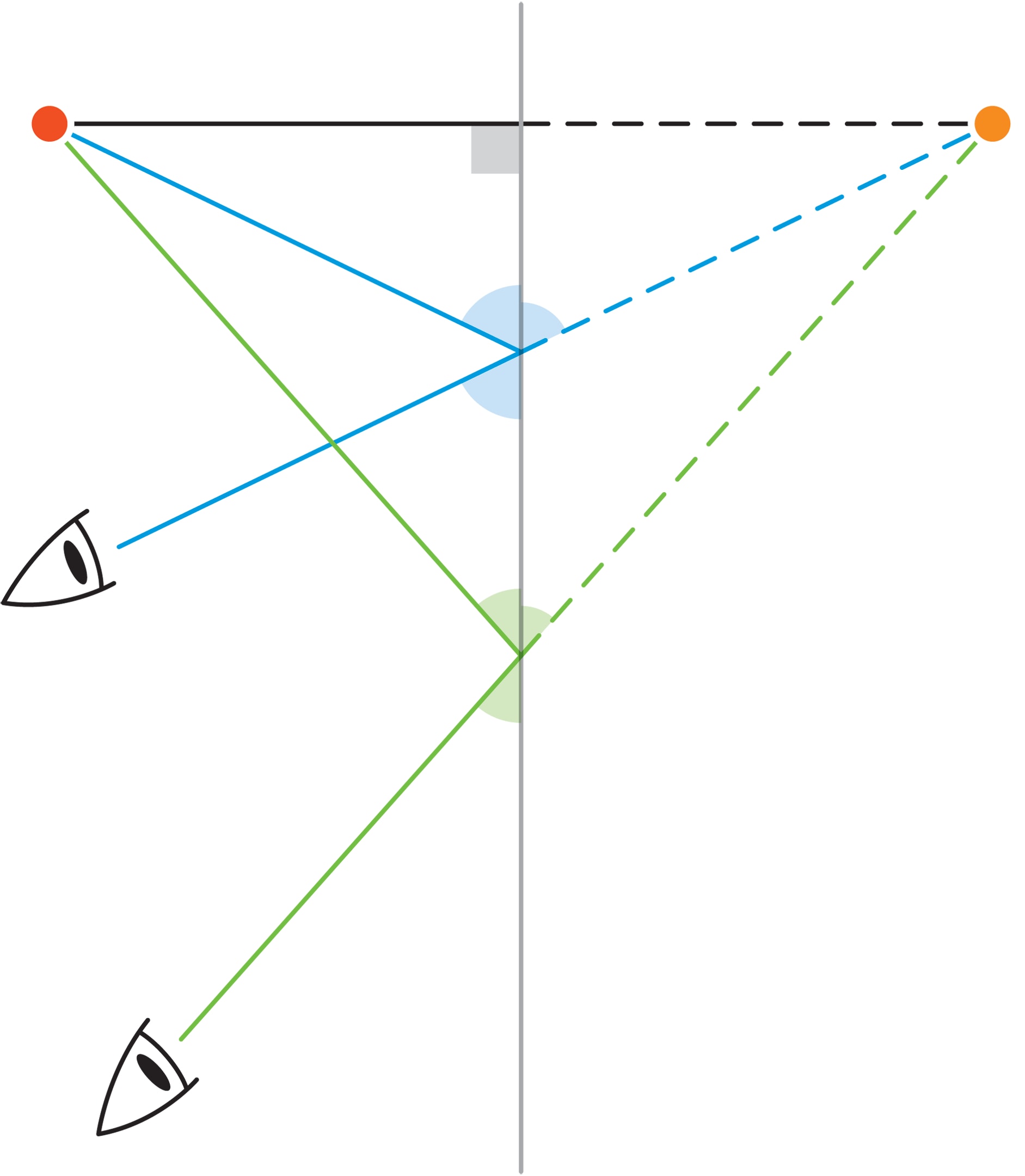
Отражение (образ) в зеркале какого-либо объекта при любом положении наблюдателя будет казаться ему реальным, неподвижным объектом, находящимся в пространстве за зеркалом и расположенным симметрично оригиналу относительно плоскости зеркала.
Реальный мир, отражаясь в зеркале, в свою копию переносит и все правила игры. В частности, отражение зеркала в зеркале будет служить зеркалом в зазеркалье, образы предметов будут отражаться в нём по обычным законам оптики.
Если имеется несколько зеркал, то их отражения друг в друге порождают цепочку виртуальных зеркал, многократные отражения в которых предмета и есть набор его видимых образов.
У калейдоскопа разноцветные предметы лежат в основании призмы, следовательно, их отражения не выходят за пределы плоскости основания. Поэтому в дальнейшем будем считать, что отражения происходят в плоском мире относительно прямых (зеркал). Самое главное — то, что два зеркальных луча, образующих угол $α$, и их взаимные отражения порождают образуют веер зеркал с общей вершиной и угловым шагом $α$.
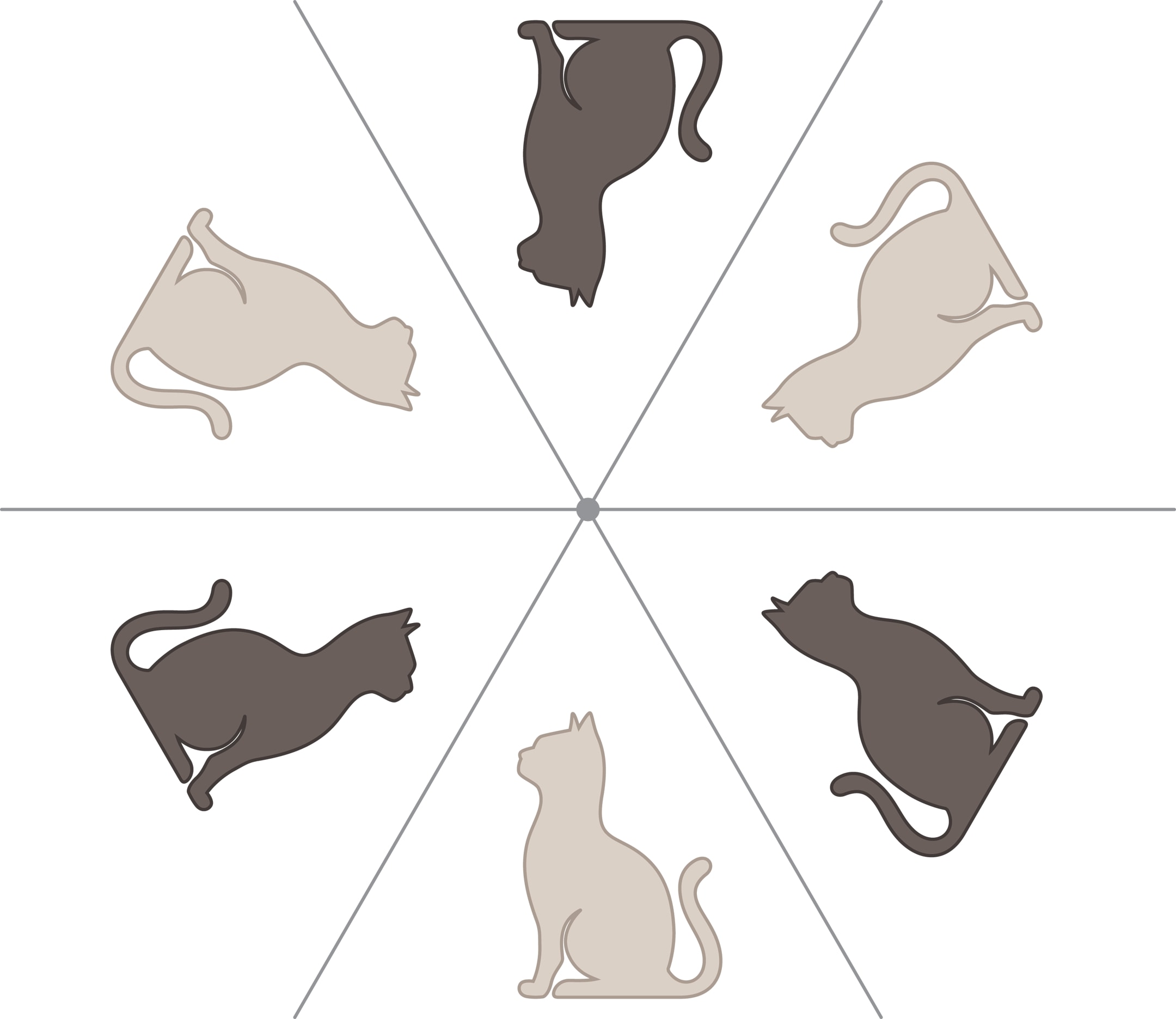
При отражении в зеркале фигуры (картинки) меняется её ориентация, но два последовательных отражения в соседних зеркалах веера — просто поворот на угол $2α$. Чтобы картинка после выполнения $n$ таких поворотов перешла в себя, должно выполняться соотношение $2α\cdot n=2π$, т. е. $α={π}/{n}$, где $n$ — натуральное число ($n\ge 2$).
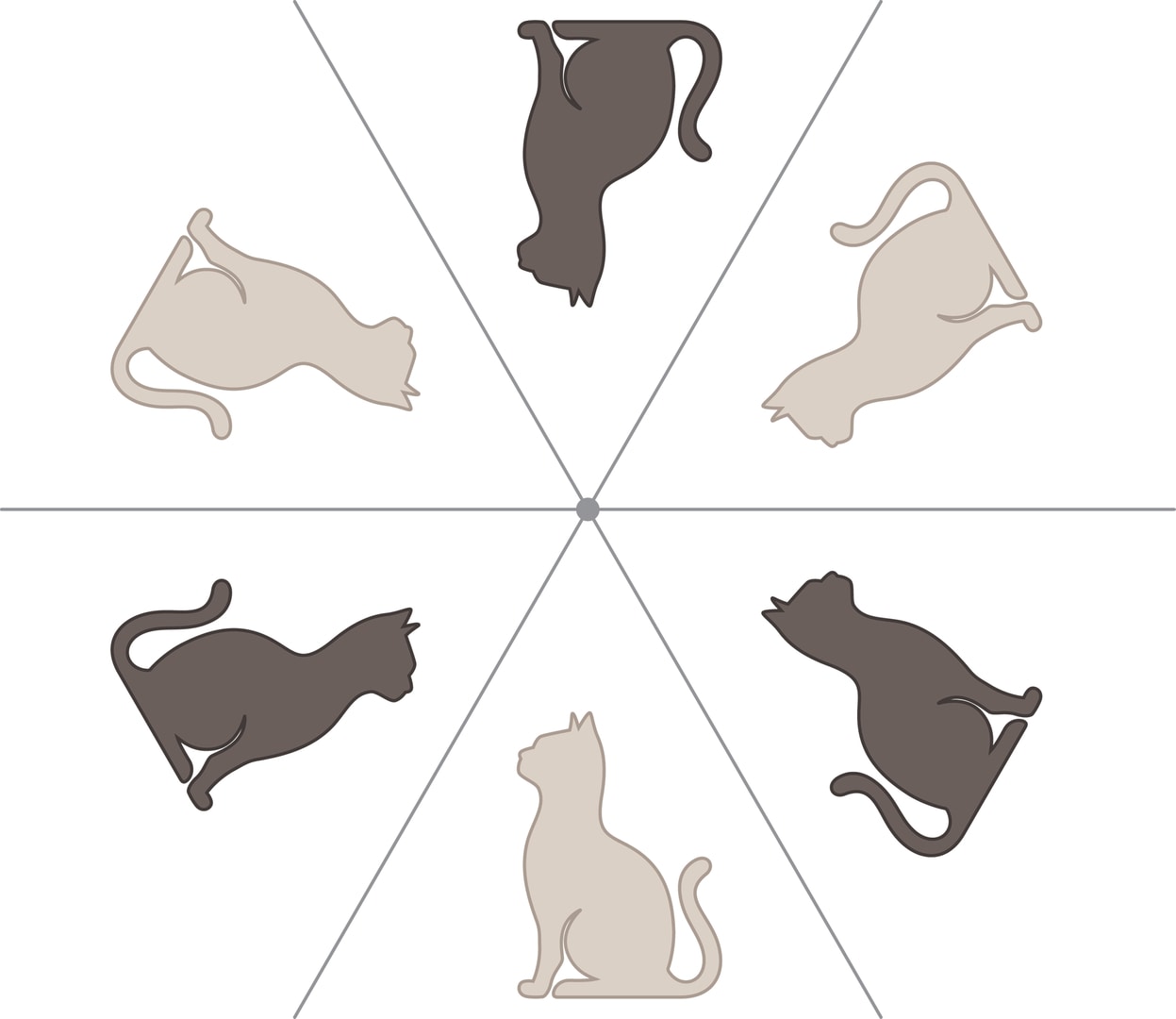
В этом случае настоящие и виртуальные зеркала разбивают плоскость на $2n$ равных углов, в каждом из которых возникает образ картинки.
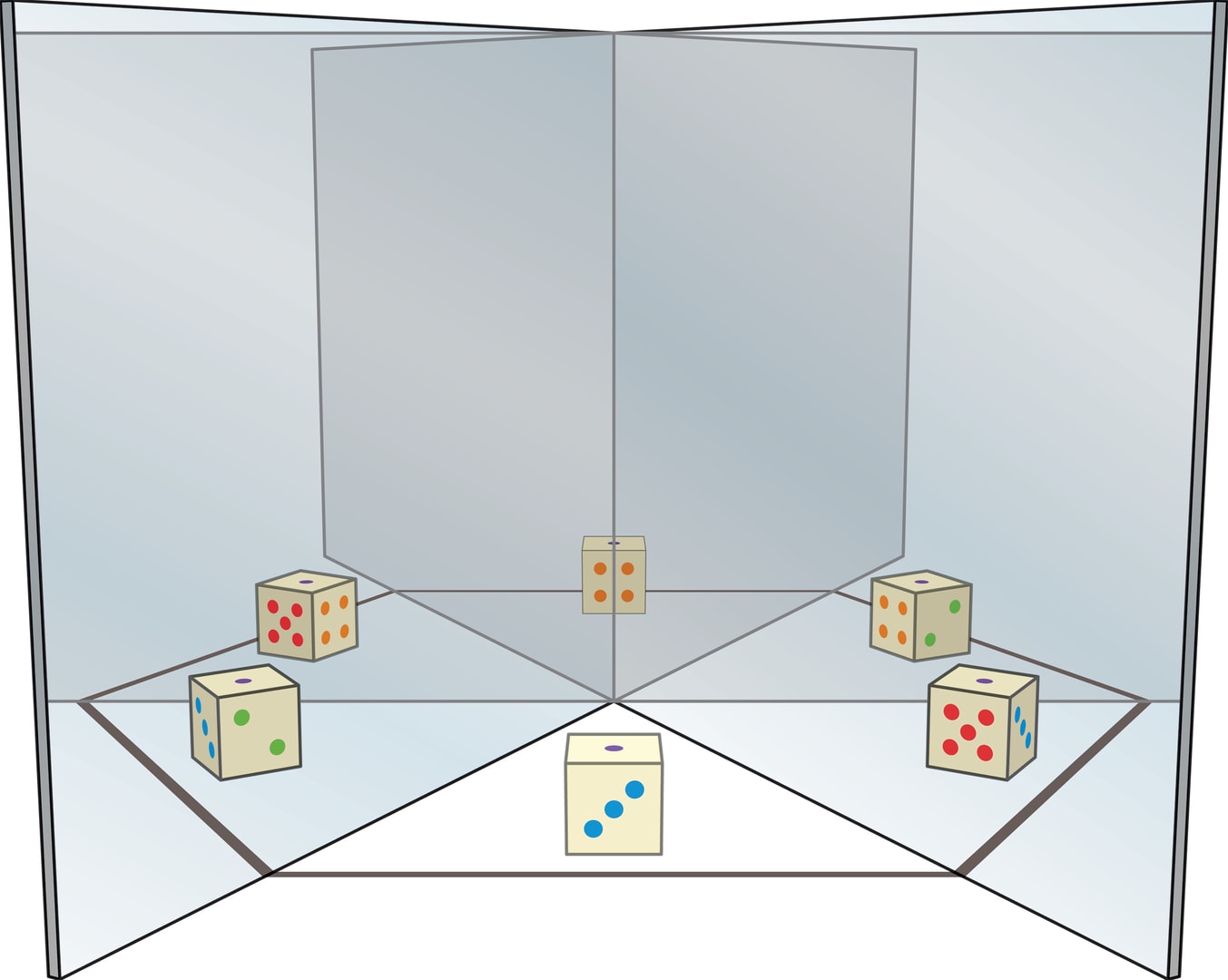
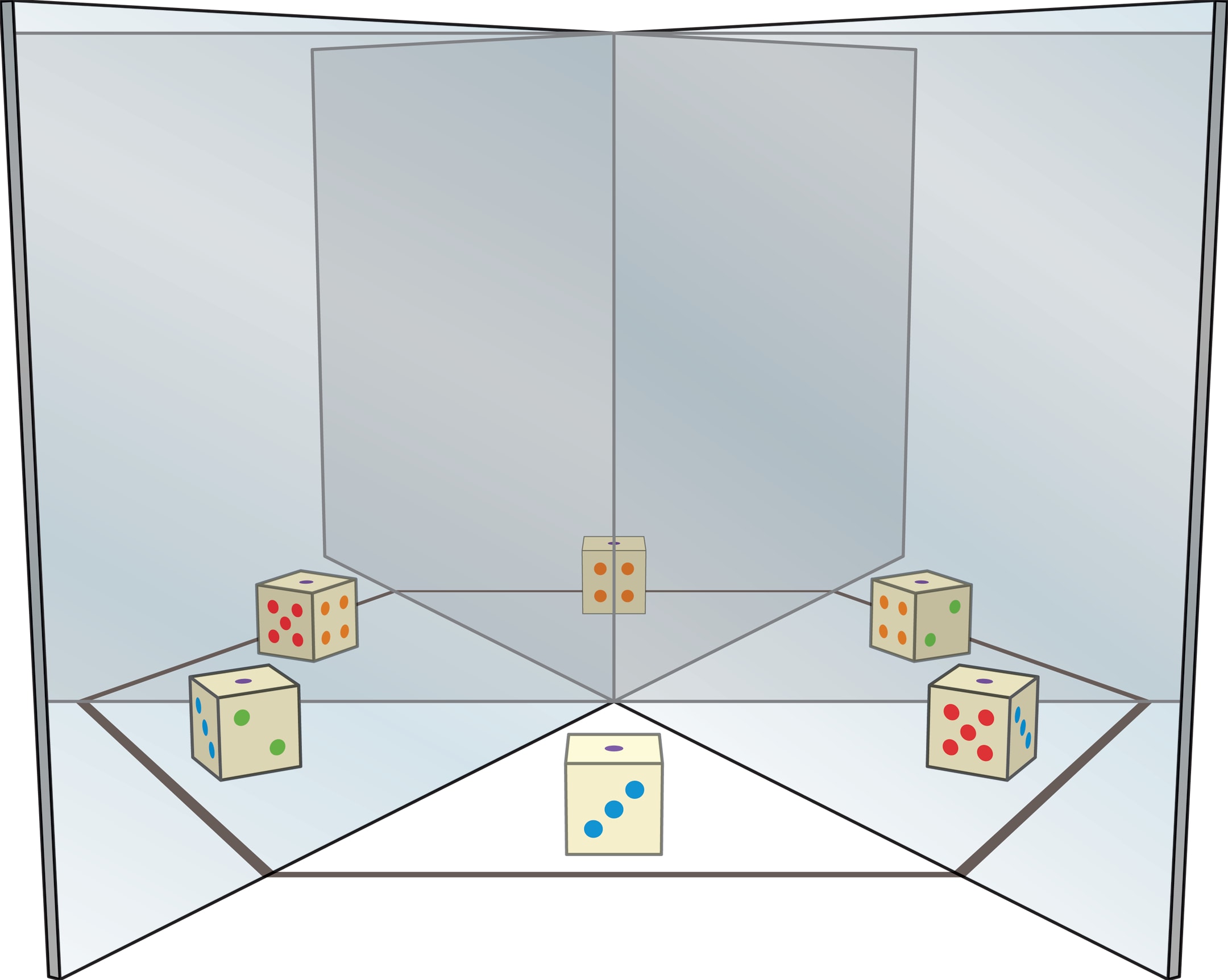
Чтобы эти факты и формулы ожили, можно провести серию опытов. Поставьте на стол два прямоугольных зеркальца, сложив их как распахнутую книжку, и загляните в неё. Вы увидите ряд виртуальных зеркал, число которых можно менять, увеличивая или уменьшая угол между зеркальными «страницами» книжки. А если междуними положить небольшой предмет, то и он будет «клонирован». Причём трёхмерный объект «клоны» представят с разных сторон. Например, у игрального кубика вы можете увидеть сразу пять граней из шести.
Отсутствие перекрытий при отражениях фигур в случае двух зеркал, образующих «правильный» угол вида $\frac{π}{n}$, является основой калейдоскопа.
Если основанием зеркальной призмы служит многоугольник, то условие «правильности» всех его углов необходимо для того, чтобы не перекрывались изображения, получаемые многократными отражениями его внутренности относительно сторон. Можно показать, что это условие является и достаточным.
Итак, задача описания всех возможных конструкций калейдоскопов сводится к описанию многоугольников-оснований, у которых все углы «правильные».
Многоугольники с числом сторон пять и более не подходят, поскольку углы вида $\frac{π}{n}$ не больше, чем $\frac{π}{2}$, при $n\ge 2$. Из четырёхугольников подходят только прямоугольники.
В случае треугольников основой решения задачи служит то, что сумма углов любого треугольника равна $π$. Если все углы «правильные», то, обозначив их $\frac{π}{k}$, $\frac{π}{m}$, $\frac{π}{n}$, получаем уравнение $$ \frac{1}{k}+\frac{1}{m}+\frac{1}{n}=1. $$
Трём его решениям (3, 3, 3), (2, 4, 4) и (2, 3, 6) соответствуют три возможных треугольных основания калейдоскопа: равносторонний треугольник с углами $\left(\frac{π}{3}, \frac{π}{3}, \frac{π}{3}\right)$, прямоугольные треугольники с углами $\left(\frac{π}{2}, \frac{π}{4}, \frac{π}{4}\right)$ и $\left(\frac{π}{2}, \frac{π}{3}, \frac{π}{6}\right)$.
Это уже упоминавшийся «модельный» набор $60°$—$60°$—$60°$, $90°$—$45°$—$45°$ и $90°$—$60°$—$30°$.
Разноцветная «начинка» таких треугольников (прямоугольника) в основании калейдоскопа может быть превращена в узор, видимый в калейдоскопе, с помощью рисования или компьютерной графики — нужно последовательно отражать треугольник (с картинкой внутри) относительно сторон, изначальных и возникающих. При этом последовательность отражений может быть любой — узор будет получаться один и тот же! А счастливый обладатель калейдоскопа увидит через окуляр этот узор как реальный и устойчивый, не меняющийся при лёгком наклоне головы наблюдателя.
Описанный калейдоскоп — по существу двумерный, поскольку видимый в нём узор — плоский. Чисто математически, не заботясь о практической реализации, можно говорить о калейдоскопах и в многомерных мирах, и в «искривлённых» пространствах, например на сфере или на плоскости Лобачевского. Эти задачи не являются искусственными, они тесно связаны с различными разделами математики (от теории групп и теории функций комплексного переменного до теории чисел и алгебраической геометрии).
Калейдоскопы в евклидовых пространствах или на сфере любой размерности уже детально изучены. А полное описание калейдоскопов в пространствах Лобачевского ещё не завершено, хотя калейдоскопические узоры на плоскости Лобачевского можно увидеть даже в музеях, на гравюрах знаменитого голландского художника Маурица Эшера.
Результатом изучения радующей глаз игрушки стало появление целого математического раздела — теории дискретных групп, порождённых отражениями.
Винберг Э. Б. Калейдоскопы и группы отражений
Винберг Э. Б. Калейдоскопы
Группа диэдра
Калейдоскоп