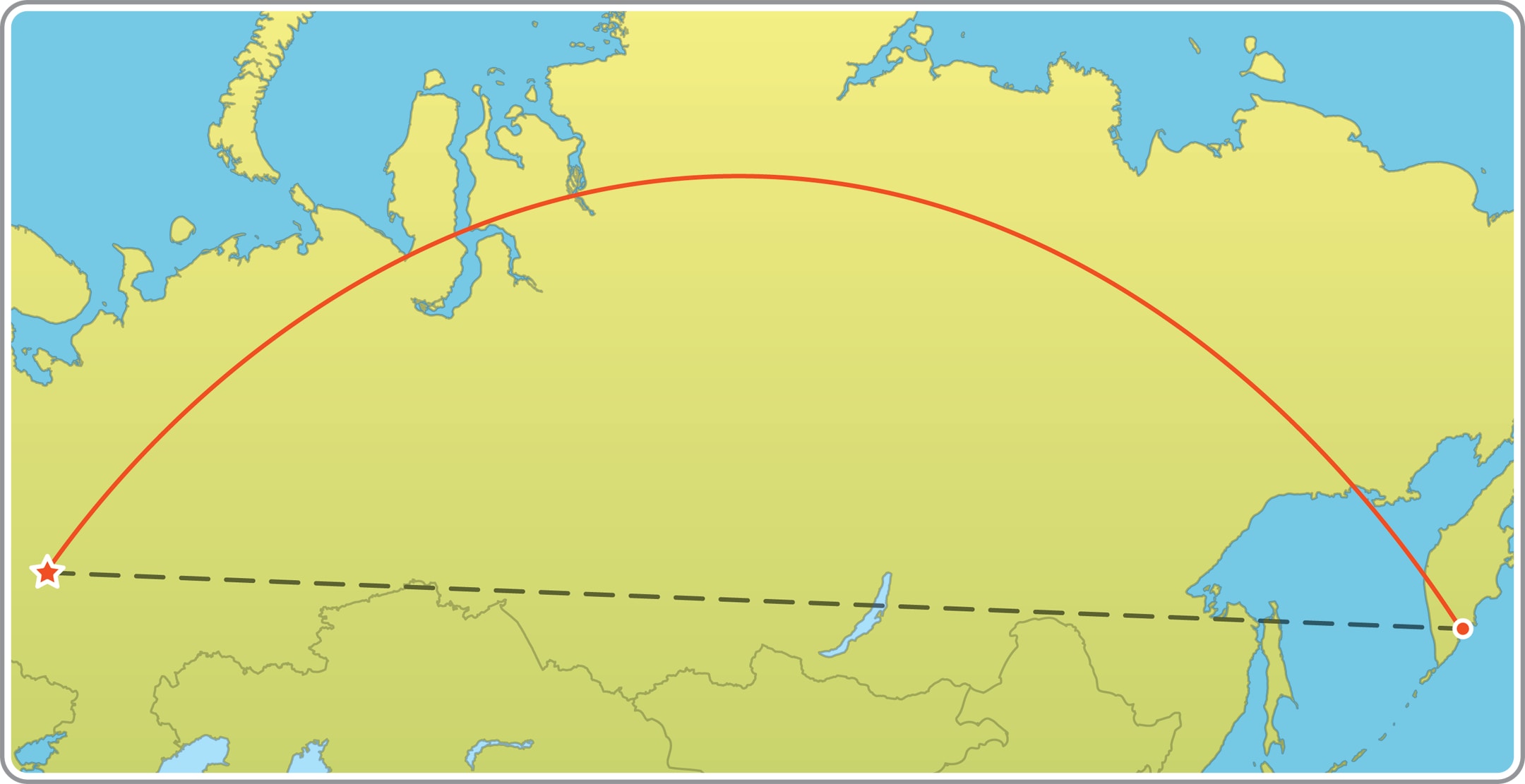
Если проследить по карте маршрут полёта самолёта из Москвы в Петропавловск-Камчатский, то можно заметить, что во время полёта самолёт забирается (по широте) высоко вверх. Кажется, что длина такого пути больше длины «прямого» пути, соединяющего на карте эти два города (координаты по широте близки: $55° 45'$ с. ш. и $53° 1'$ с. ш.).
Странно, ведь лишние сотни километров пути самолёта — дорогое удовольствие. Но и сервис «Яндекс.Карты» на запрос о расстоянии между этими городами тоже выдаёт выпуклую вверх кривую.
Всё дело в том, что понятие кратчайшего расстояния неразрывно связано с той поверхностью, по которой оно измеряется. Любая плоская карта представляет земную поверхность с искажениями. А рассмотрение соответствующих траекторий на глобусе позволит во всём разобраться.
Чтобы найти кратчайшее расстояние между двумя точками на сфере, необходимо провести через них большую окружность. Так называют окружность, образованную пересечением сферы с плоскостью, проходящей через центр сферы и выбранные точки. Меньшая из двух дуг большой окружности, соединяющая точки, является кратчайшим расстоянием на сфере между ними. В математике линию, реализующую минимальное расстояние между двумя точками на рассматриваемой поверхности, называют геодезической.
Все остальные маршруты, соединяющие Москву и Петропавловск-Камчатский, в том числе тот, который казался прямым на карте, на глобусе (и в реальности!) будут длиннее этой дуги. Итак, кратчайшая траектория полёта самолёта определяется дугой большой окружности.
На практике авиакомпании не всегда удаётся выбрать «геодезический» маршрут между двумя городами. Приходится учитывать и другие многочисленные условия и обстоятельства, постоянные и меняющиеся: наличие запретных для полёта зон; особые правила полёта над океаном и правила для самолётов с двумя двигателями (регламентируется максимальная удалённость маршрута от аэропортов); стоимость диспетчерского обслуживания при пересечении воздушного пространства той или иной страны; загруженность воздушных перекрёстков; погодные условия.
Можно ощутить, насколько реальный маршрут из Москвы в Петропавловск-Камчатский забирается на север, если отметить на карте города, над которыми он пролегает: Ярославль, Котлас, Сыктывкар, Ухта, Салехард, Норильск, Магадан.
Кривизна поверхности Земли рассматривается с точки зрения геометрии в статье «Искривлённые миры». В статье «Картографические проекции» рассказано о способах отображения земной поверхности на плоских картах.
В полётах самолётов есть математическая составляющая, в жизни пилотов — профессиональная и эмоциональная составляющие. Яркие рассказы об этом мире оставили профессиональные лётчики. Антуан де Сент-Экзюпери, которого все знают как автора «Маленького принца», написал роман «Южный почтовый». Василий Васильевич Ершов, много лет летавший в небе Восточной Сибири, написал о «лётной» жизни ряд книг, название одной из них — «Раздумья ездового пса».