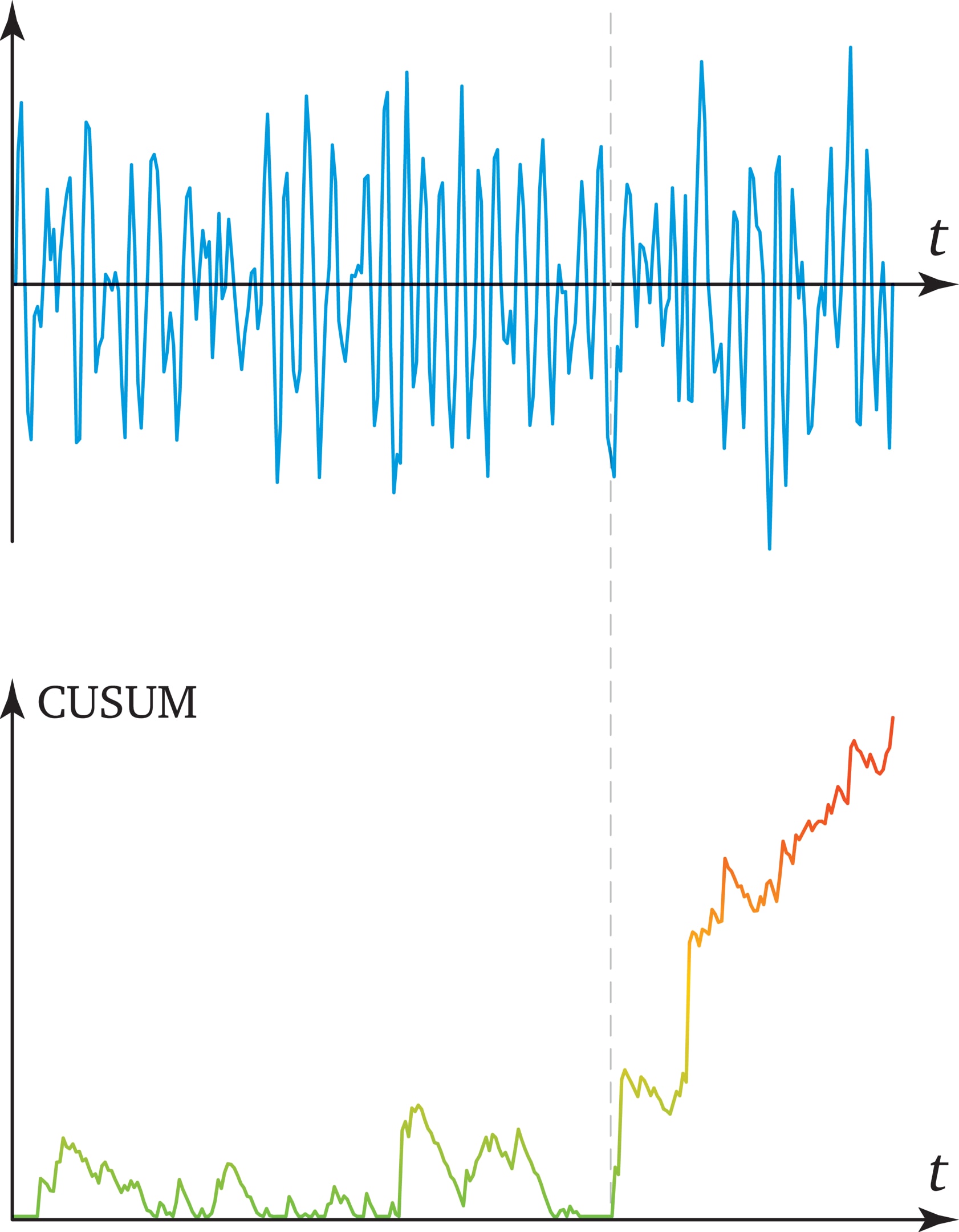
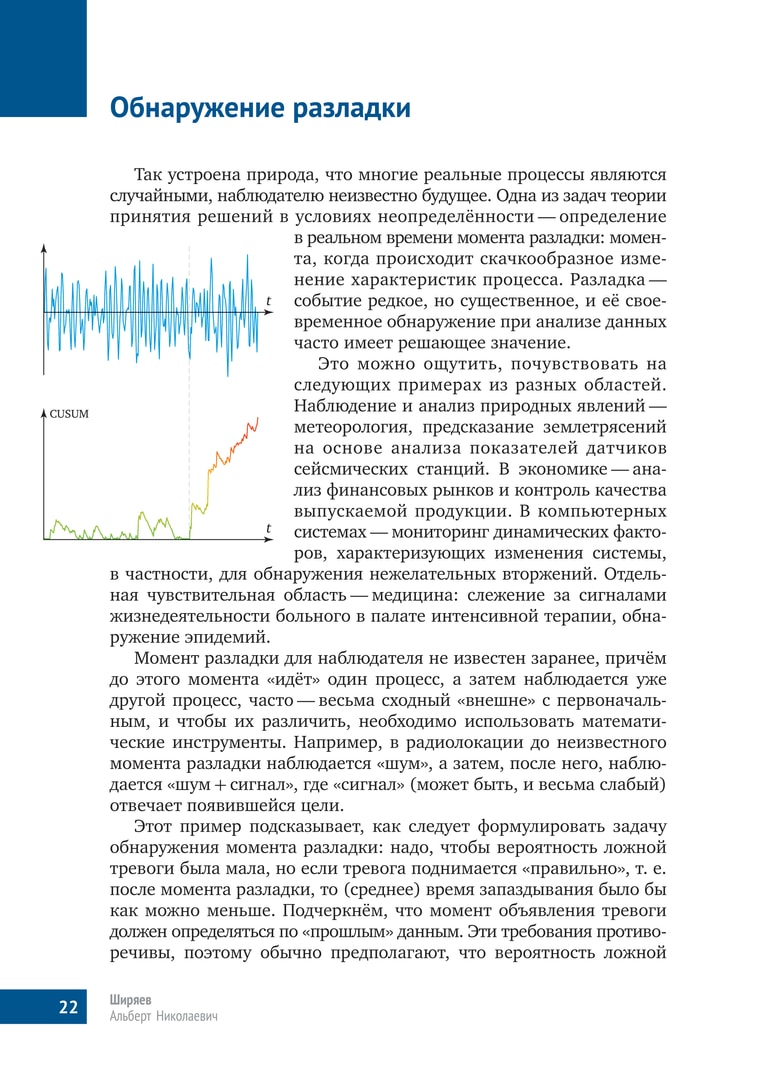
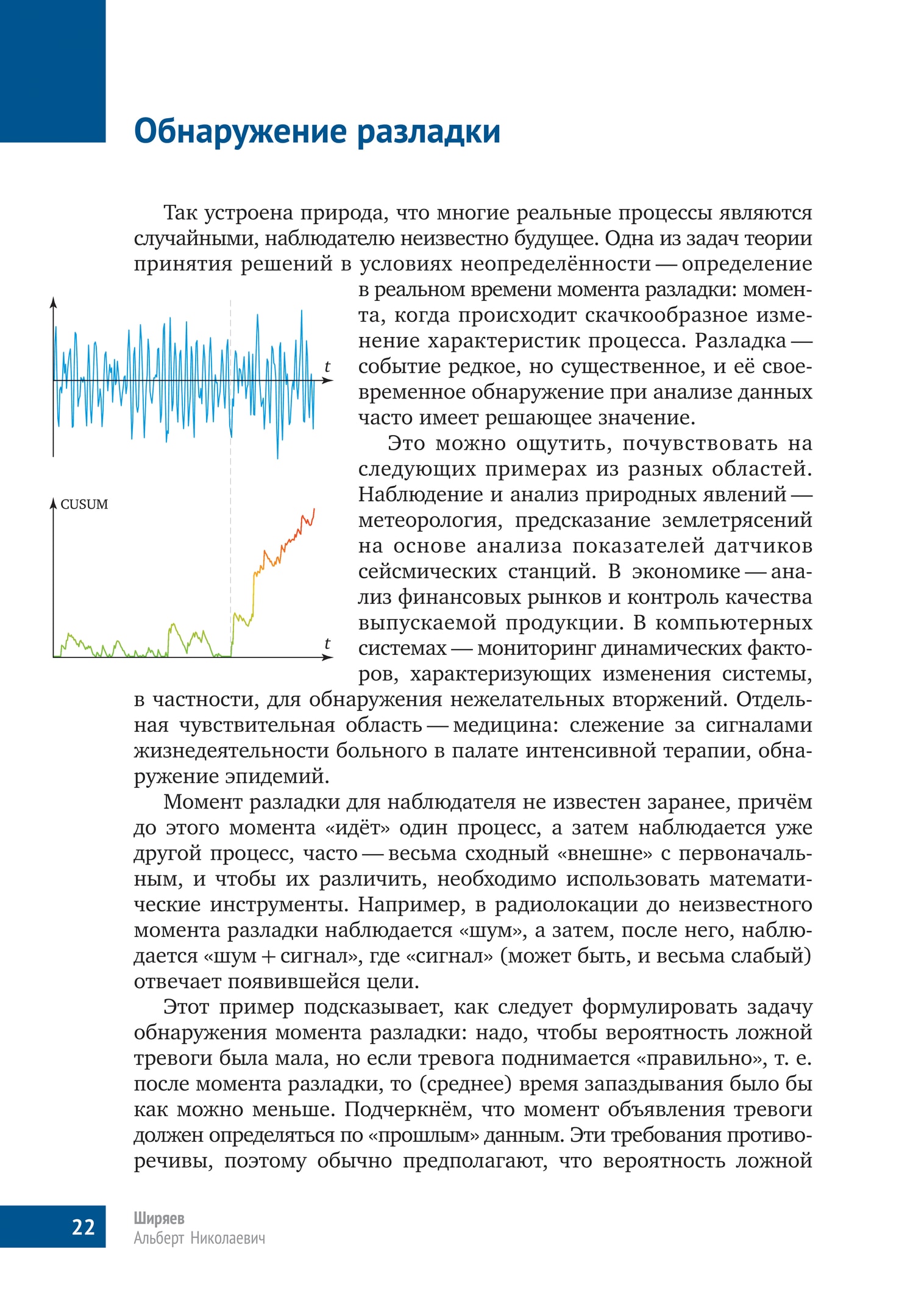
Так устроена природа, что многие реальные процессы являются случайными, наблюдателю неизвестно будущее. Oдна из задач теории принятия решений в условиях неопределённости — определение в реальном времени момента разладки: момента, когда происходит скачкообразное изменение характеристик процесса. Разладка — событие редкое, но существенное, и её своевременное обнаружение при анализе данных часто имеет решающее значение.
Это можно ощутить, почувствовать на следующих примерах из разных областей. Наблюдение и анализ природных явлений — метеорология, предсказание землетрясений на основе анализа показателей датчиков сейсмических станций. В экономике — анализ финансовых рынков и контроль качества выпускаемой продукции. В компьютерных системах — мониторинг динамических факторов, характеризующих изменения системы, в частности, для обнаружения нежелательных вторжений. Отдельная чувствительная область — медицина: слежение за сигналами жизнедеятельности больного в палате интенсивной терапии, обнаружение эпидемий.
Момент разладки для наблюдателя не известен заранее, причём до этого момента «идёт» один процесс, а затем наблюдается уже другой процесс, часто — весьма сходный «внешне» с первоначальным, и чтобы их различить, необходимо использовать математические инструменты. Например, в радиолокации до неизвестного момента разладки наблюдается «шум», а затем, после него, наблюдается «шум + сигнал», где «сигнал» (может быть, и весьма слабый) отвечает появившейся цели.
Этот пример подсказывает, как следует формулировать задачу обнаружения момента разладки: надо, чтобы вероятность ложной тревоги была мала, но если тревога поднимается «правильно», т. е. после момента разладки, то (среднее) время запаздывания было бы как можно меньше. Подчеркнём, что момент объявления тревоги должен определяться по «прошлым» данным. Эти требования противоречивы, поэтому обычно предполагают, что вероятность ложной тревоги не больше некоторого малого значения, и надо минимизировать среднее время запаздывания момента поднятия тревоги.
Великий российский математик Андрей Николаевич Колмогоров в первой половине XX века предложил аксиоматику, превратившую теорию вероятностей в стройную математическую дисциплину. В середине XX века он дал строгую постановку задачи о скорейшем обнаружении разладки для винеровского процесса (математической модели многих явлений), сформулировав её как вероятностную экстремальную проблему. Тогда же появился полностью обоснованный теоретически метод обнаружения разладки и даже сам термин «разладка». Существуют и другие методы решения задачи, но возникший в школе Колмогорова метод является и конструктивным, и востребованным на практике.
Формулировка задачи обнаружения разладки в вероятностных терминах связана со случайностью значений наблюдаемых данных. Описать их разнообразный характер как-то просто вряд ли возможно, поэтому и применяется вероятностное описание, учитывающее, что эти величины — случайные, их значения меняются от одного момента времени к другому.
Методы решения задач скорейшего обнаружения в значительной мере опираются на современный аппарат теории случайных процессов, стохастического исчисления, теории мартингалов, нелинейной фильтрации и т. д. В свою очередь, многие из этих разделов получили развитие именно на пути решения задач скорейшего обнаружения. Это служит хорошей иллюстрацией того, как происходит развитие теории, когда она нацелена на решение конкретных задач, имеющих практический интерес. В общем-то, и всё развитие вероятностных дисциплин имеет сходный характер. Из истории науки известно, что зарождение теории вероятностей было связано с оценкой благоприятных исходов в азартных играх, а началом математической статистики стали попытки разрешения вопросов геодезии и астрономии.
Превративший теорию информации в область математики Клод Шеннон писал: «Сознавая, что теория информации является сильнейшим средством решения проблем теории связи (и в этом отношении её значение будет возрастать), нельзя забывать, что она не является панацеей для инженера-связиста и тем более для представителей других специальностей. Очень редко удаётся открыть одновременно несколько тайн природы одним и тем же ключом».
Мы приводим эти слова, чтобы подчеркнуть: постановки задач и известные методы их решения должны побуждать читателя формулировать новые задачи, искать для их решения новые подходы, стимулирующие развитие и собственно теоретических исследований.