В далёкой древности было замечено, что поверхность Земли не является плоской. Об этом говорило, например, такое наблюдение: когда на горизонте появляется корабль, то сначала видны верхушки мачт, и только потом появляется весь парусник. Предположение, что форма Земли — шарообразная, возникло незадолго до Пифагора. Экспериментальное подтверждение гипотезы принадлежит, видимо, Аристотелю, приводившему следующий довод. Во время лунного затмения меняющаяся граница тени Земли в каждый момент времени является дугой окружности, а только у шара граница тени при всех проекциях круговая.
Но планета — только часть трёхмерного пространства, «живущего» в четырёхмерном пространстве-времени. И в XX веке физики пришли к выводу, что фундаментальный вопрос о природе тяготения можно объяснить если связать его с кривизной пространства.
Чтобы читатель смог подойти к понятию кривизны в многомерном пространстве, рассмотрим с разных точек зрения «привычную» кривизну поверхности. На страницах книги это понятие встречалось в сюжетах «Ломтик пиццы» и «Футбольный мяч». Во многих случаях, в том числе и в утверждении о невозможности создания плоской карты Земли без искажений («Картографические проекции»), основную роль играет теорема Гаусса о кривизне.
Начнём разговор с прямого, полученного Эйлером в середине XVIII века ещё до появления теоремы Гаусса, объяснения того, что даже небольшой участок сферы не картографируется без искажений на плоскую область, т. е. его нельзя отобразить на плоскость так, чтобы сохранялись длины всех линий (а следовательно, и площади областей). Для этого достаточно проследить за «судьбой» окружности небольшого радиуса (её длиной, кругом, который она ограничивает, и его площадью).
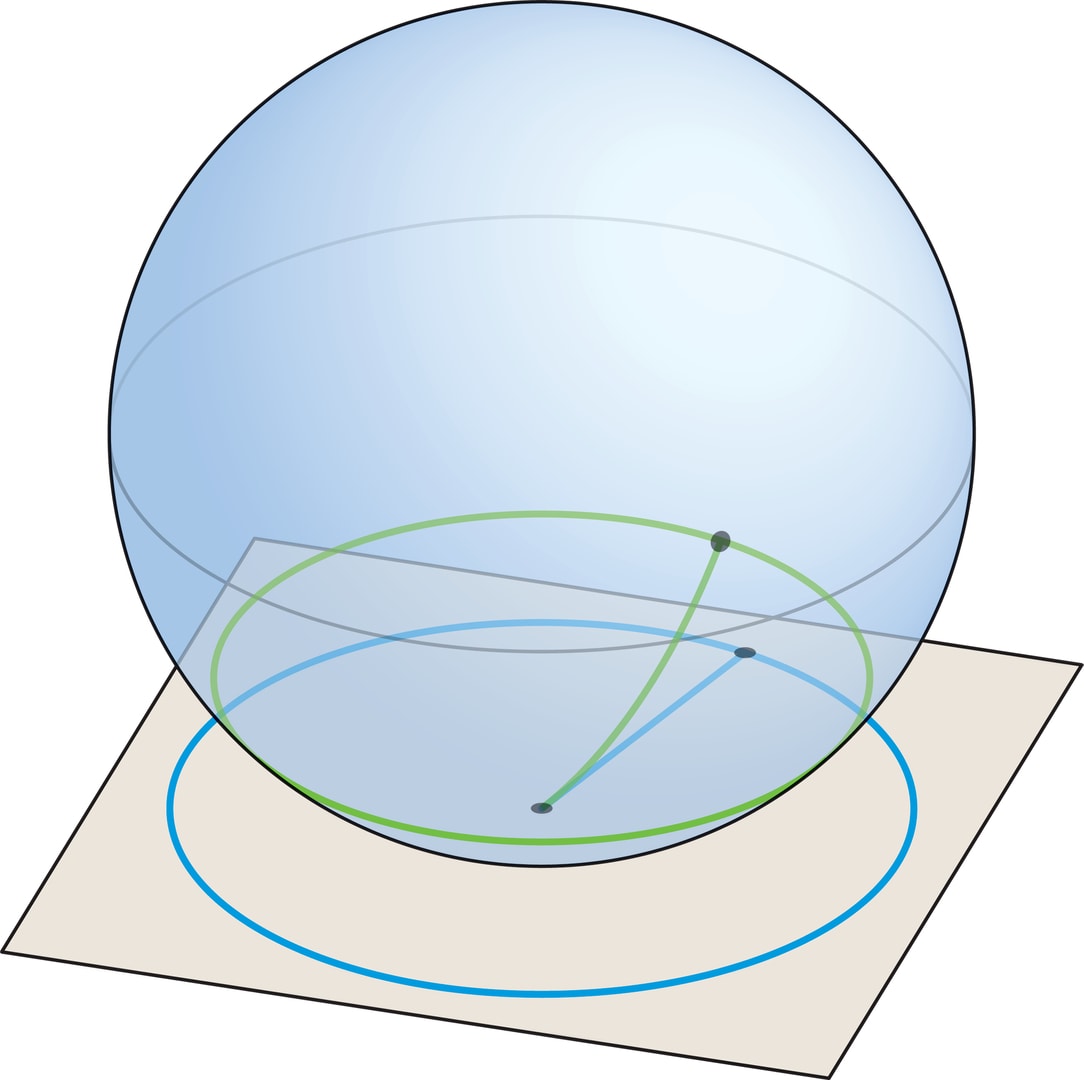
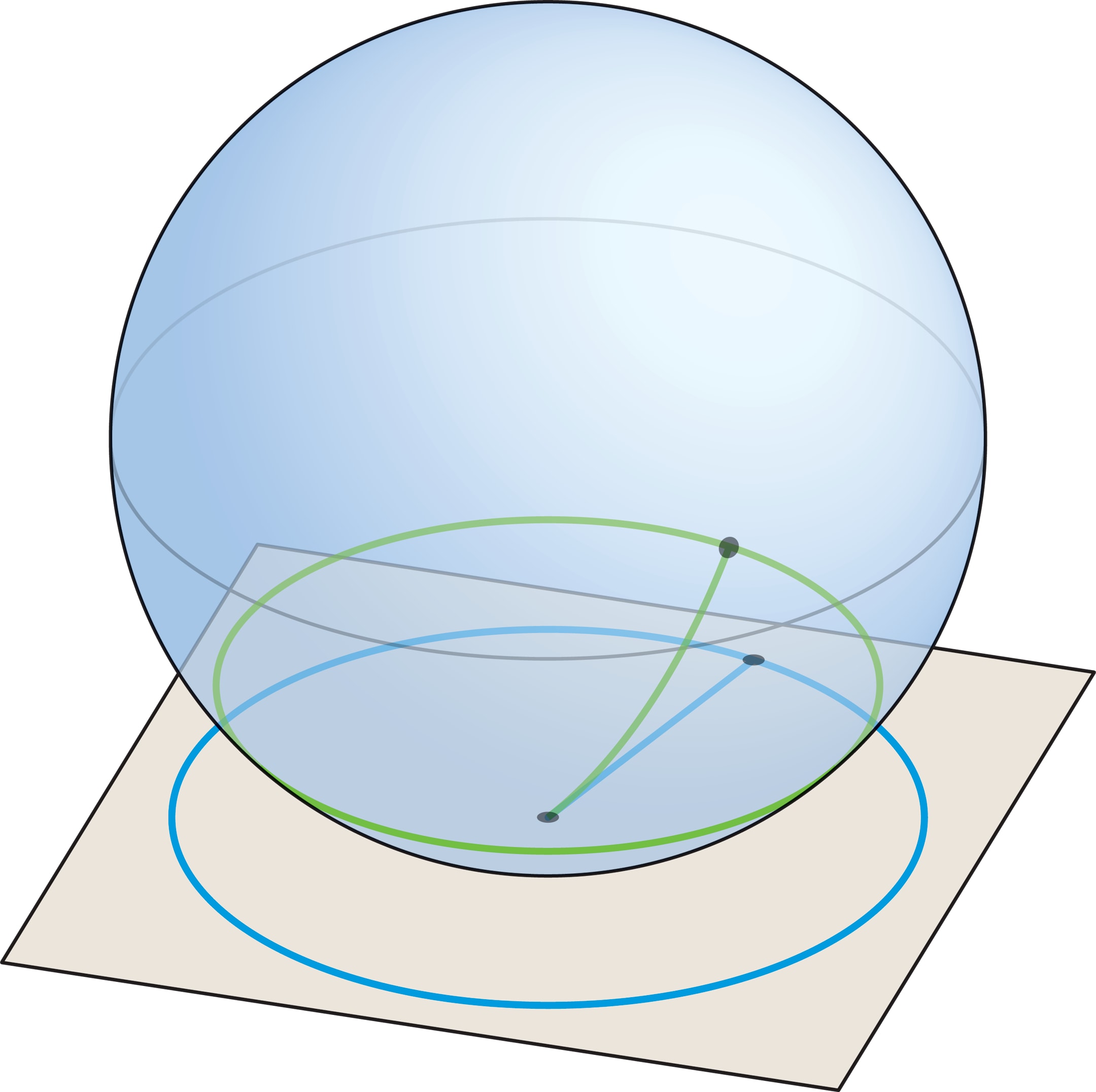
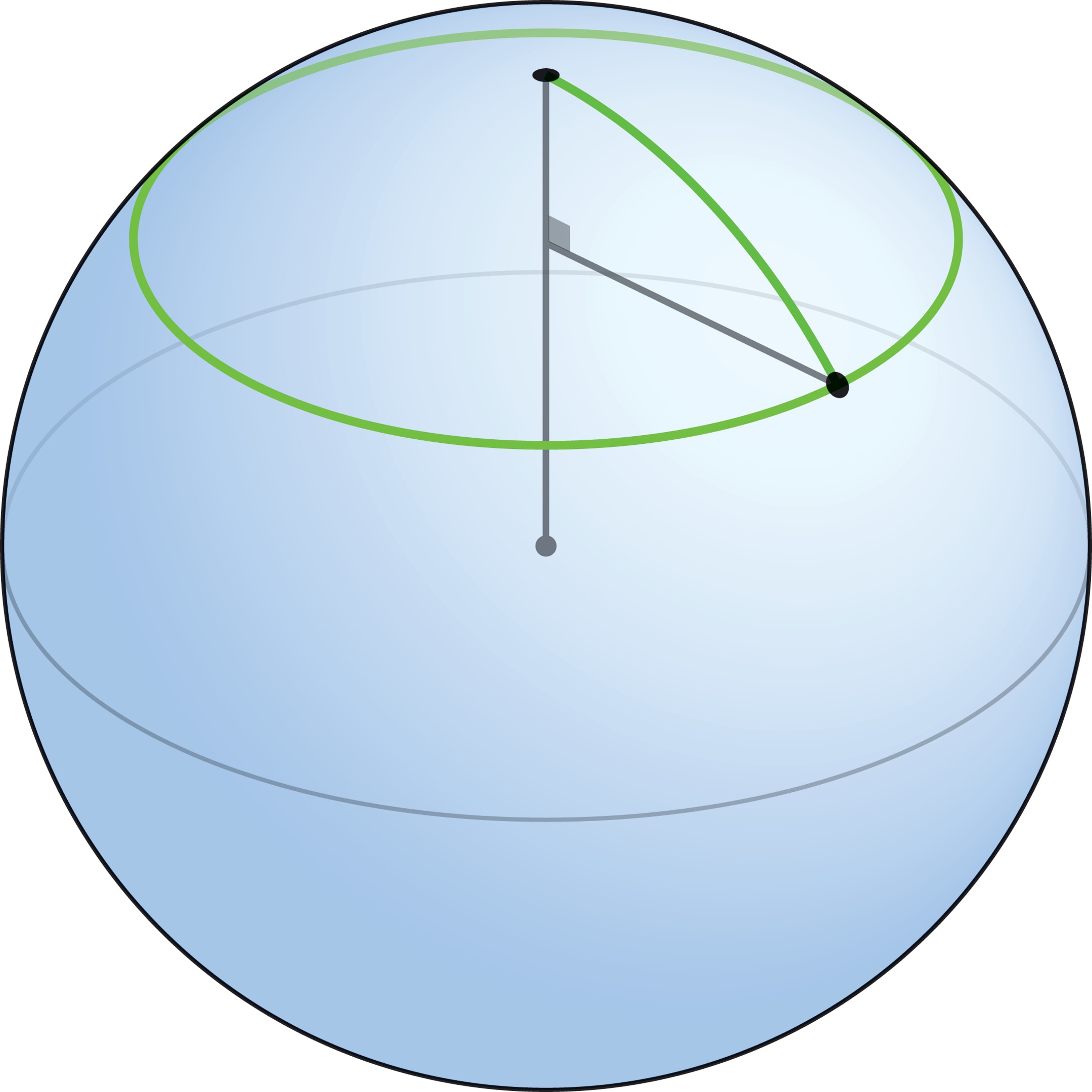
На плоскости кратчайший путь, соединяющий пару различных точек, — отрезок прямой. Точки, которые отстоят от заданной на расстояние
На плоскости окружность радиуса
Параллель состоит из точек, удалённых на расстояние
Уточним это экспериментальное доказательство с помощью аналитических формул. Из них мы увидим, как искажение длины «окружности» на сфере связано с понятием кривизны.
Расстояние между двумя точками на поверхности определяется как наименьшая из длин кривых, соединяющих эти точки и лежащих на этой поверхности. Это определение аналогично определению расстояния между точками на плоскости. На плоскости кратчайшей кривой является отрезок, соединяющий точки. На сфере кратчайшая кривая между двумя точками — это меньшая дуга большой окружности, которая получается в пересечении сферы с плоскостью, проходящей через эти точки и центр сферы.
Большие окружности на сфере и прямые линии на плоскости являются примерами геодезических. Так называются линии, у которых все достаточно короткие отрезки являются кратчайшими путями, соединящими их концы. Например, на сфере единичного радиуса большие окружности являются геодезическими, но кратчайшими путями между их концами являются дуги длины, не большей, чем
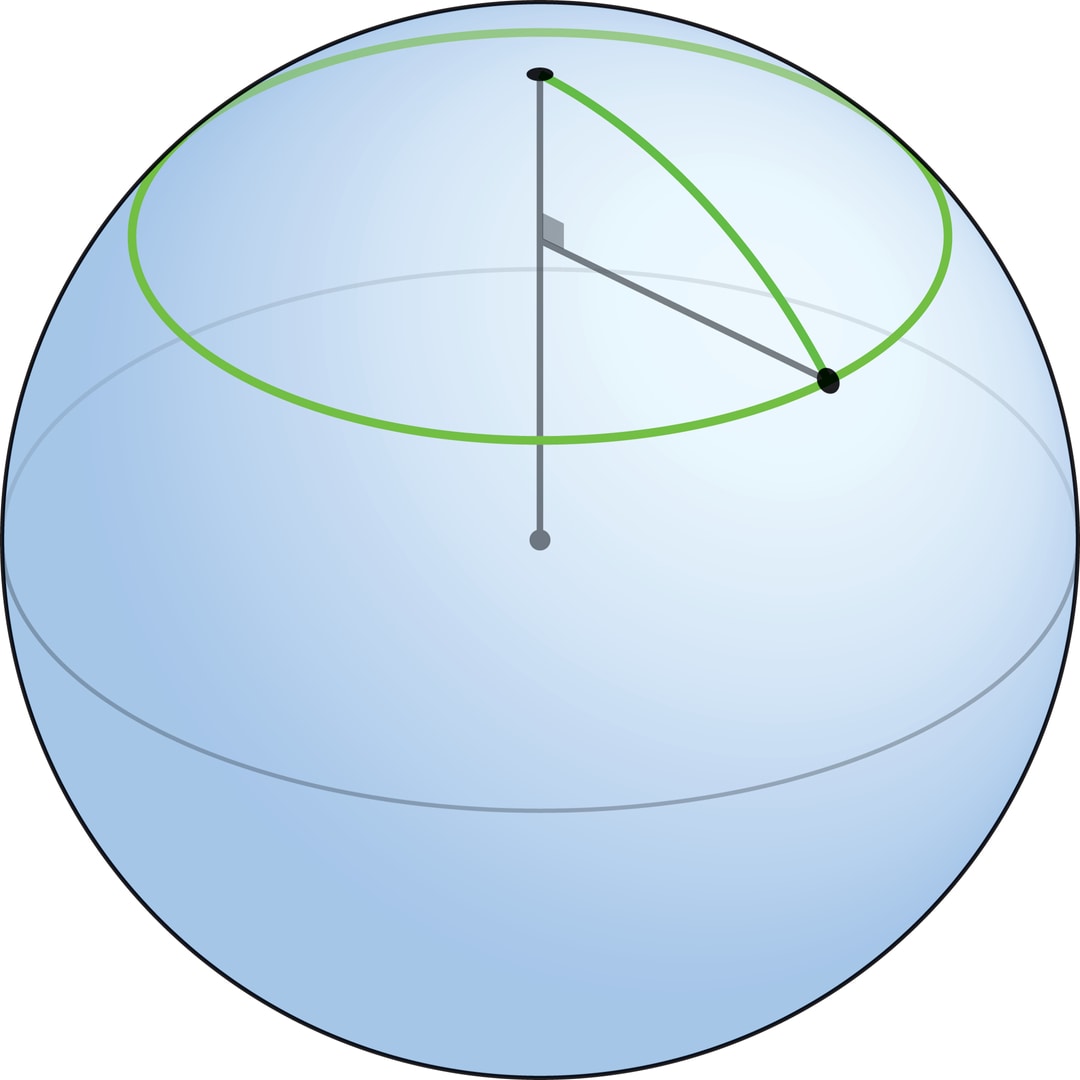
Множество точек на сфере, равноудалённых от данной точки
Вернёмся к основной задаче и ответим на вопрос, почему нельзя без искажений картографировать поверхность глобуса на плоскую область.
Например, если бы небольшую круглую шапочку, окружающую полюс на глобусе, можно было «точно» картографировать на плоскость, то образом граничной параллели
На плоскости длина окружности радиуса
Окружности радиуса
Длина параллели и площадь части сферы, которую она ограничивает, равны
Первая из формул — просто длина окружности радиуса
Углу
Подставив эти приближённые значения в формулы для
Видно, что
При малых значениях
где
В общем случае гауссова кривизна зависит от точки поверхности. Поверхностями постоянной кривизны, например, являются сферы — для них кривизна в каждой точке равна
Ещё одну трактовку кривизны даёт сравнение треугольников на плоскости и в сферическом мире. Например, отличие сферы (как и любой другой «кривой поверхности») от плоскости проявится, если сравнить на этих поверхностях результаты параллельного переноса вектора вдоль замкнутого пути.
Параллельный перенос вектора из одной точки в другую вдоль геодезической реализуется семейством векторов, приложенных ко всем точкам отрезка геодезической так, что их длины и угол между векторами и геодезической сохраняются. (В начальной точке вектор семейства совпадает с данным вектором.)
Для плоскости это определение совпадает с обычным «школьным» определением параллельного переноса. При переносе вектора вдоль сторон треугольника он перейдёт сам в себя. Но в искривлённом пространстве, например на сфере, это уже не так.
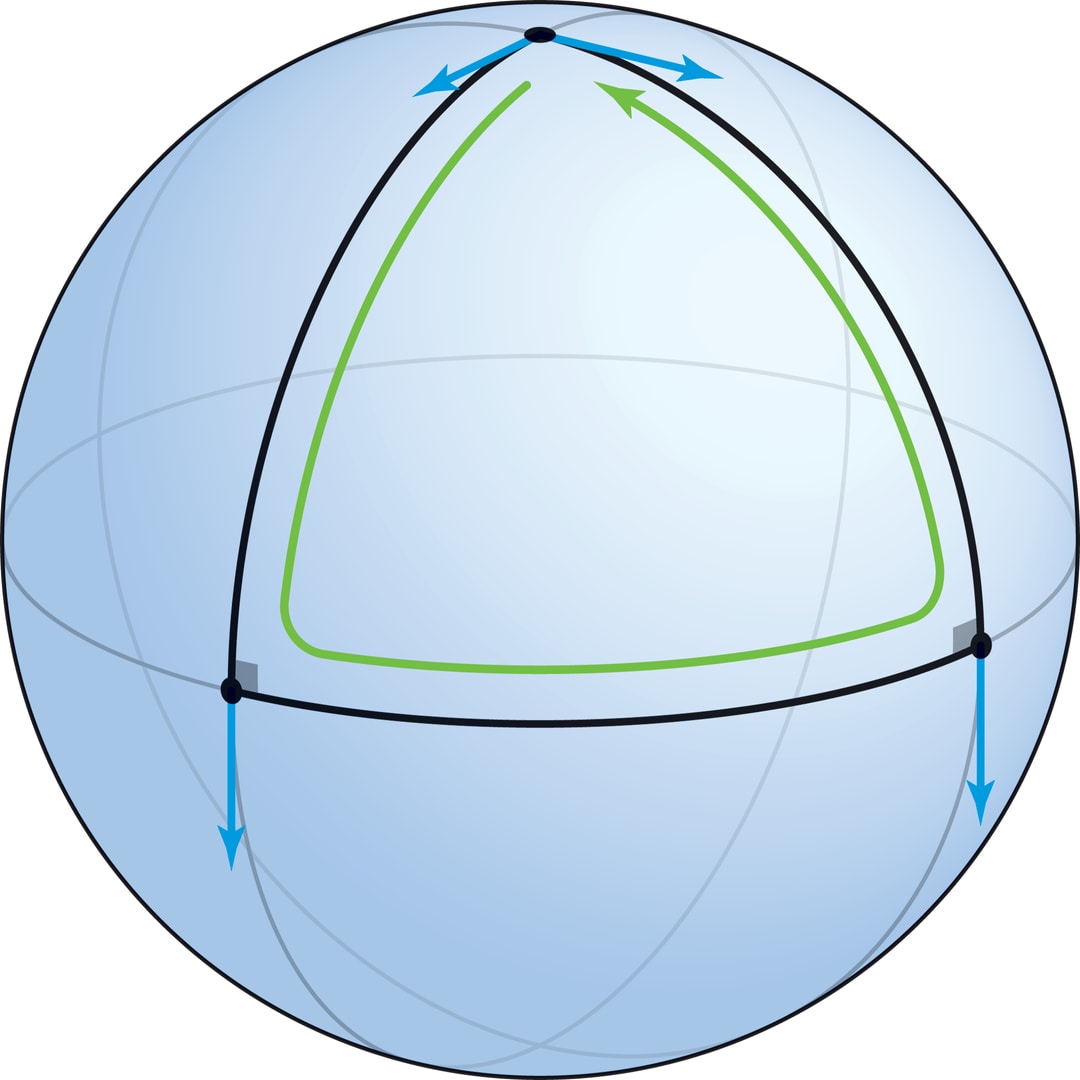
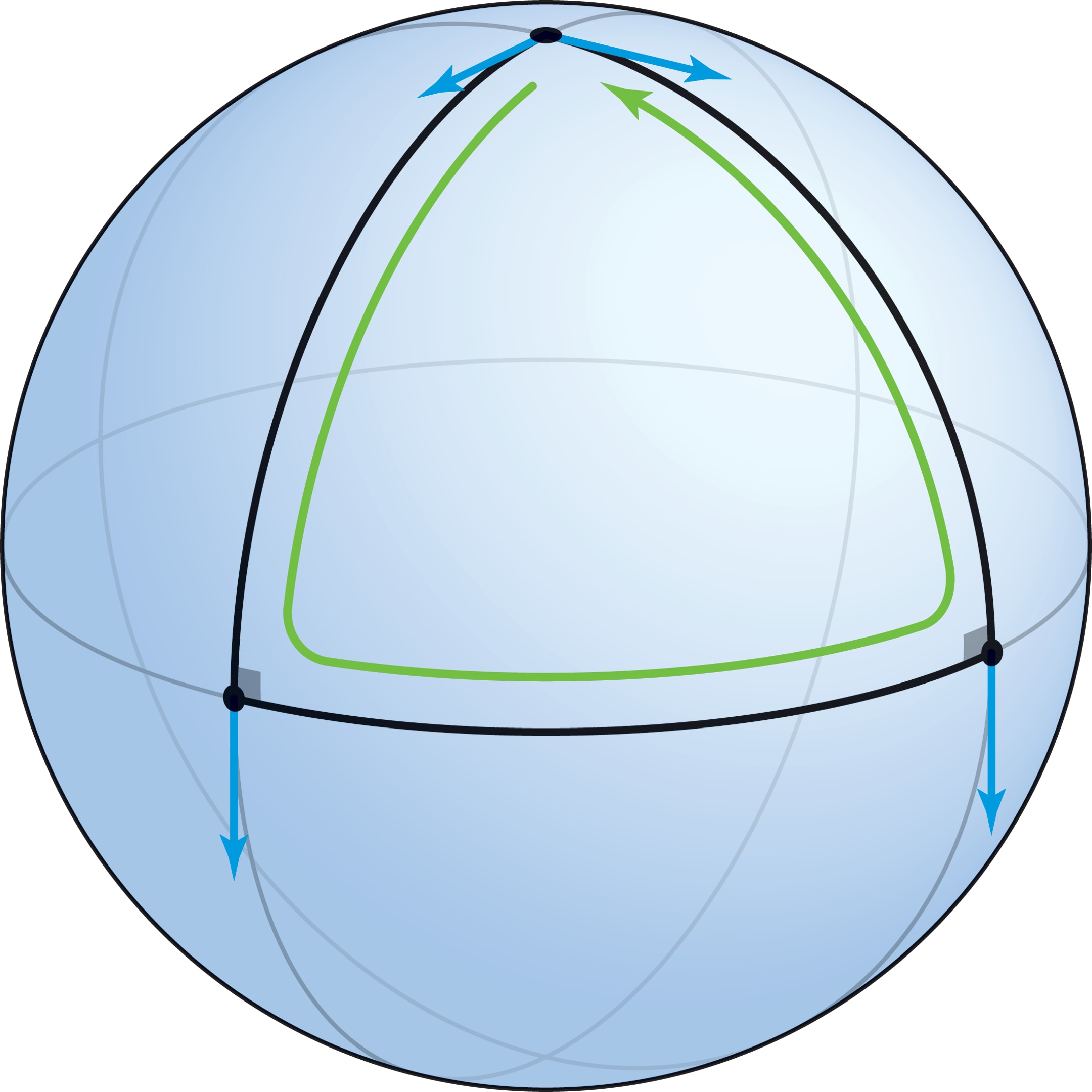
Сферическим треугольником называется фигура, ограниченная дугами трёх больших окружностей (стороны треугольника — отрезки геодезических, кратчайшие пути, соединяющие вершины). Рассмотрим треугольник, ограниченный двумя меридианами, выходящими из полюса под углом
В рассмотренном треугольнике сумма углов равна
Отталкиваясь от того, что площадь поверхности сферы радиуса
В евклидовой геометрии через точку, лежащую вне заданной прямой, можно провести прямую, параллельную данной, и притом только одну. В этом состоит аксиома о параллельных прямых (она ещё известна как «пятый постулат» Евклида). Отрицать аксиому Евклида можно двумя способами: либо утверждать, что через точку не проходит ни одна параллельная прямая, либо — что проходит несколько параллельных прямых.
Первый вариант реализуется в сферической геометрии: аналоги прямых — большие окружности (геодезические). Любая пара таких линий пересекается в двух точках, т. е. параллельных «прямых» нет. Но надо отметить, что в сферической геометрии нарушается ещё более важный принцип — единственность прямой, проходящей через две точки. На сфере через диаметрально противоположные точки проходит бесконечно много «прямых» — больших окружностей.
Другая форма отказа от постулата о параллельных прямых стала основой геометрии, теоретически построенной Николаем Ивановичем Лобачевским. (Первые примеры пространств, в которых геометрия Лобачевского реализуется, были найдены только через сорок лет после первых работ Лобачевского о «воображаемой геометрии».)
Лобачевский вывел все аналитические формулы новой теории, оснастил её вычислительными инструментами. Оказалось, что если понимать под треугольниками фигуры, составленные из трёх отрезков геодезических, то возникают нетривиальные соотношения между длинами сторон и углами треугольников, которых нет в евклидовой геометрии. В частности, сумма углов треугольника всегда меньше, чем
Французский математик Лежандр, пытаясь вывести постулат о параллельных из других аксиом Евклида, доказал, что если существует хотя бы один треугольник с суммой углов, равной
Аналоги рассмотренных на сфере функций
Правильное обобщение кривизны на многомерные пространства основано на понятии параллельного переноса. Мы уже продемонстрировали, что на круглой (обычной) сфере такой перенос вектора вдоль замкнутого пути, вообще говоря, не переводит его в себя, а различие двух векторов связано с кривизной сферы.
В современной физике одно из основных положений состоит в том, что сила тяготения (притяжения), физическое взаимодействие, по сути есть геометрическая характеристика нашего пространства — его кривизна.
