В 2011 году Нобелевская премия по химии была присуждена «за открытие квазикристаллов» — твёрдых тел с атомной структурой, не встречавшейся ранее.
Это открытие начало новую страницу в изучении твёрдых тел. Твёрдые вещества делятся на два типа: кристаллы и тела с аморфной структурой (стёкла, пластики). Различие между кристаллом и аморфным телом, замеченное в древности, состоит в том, что кристаллы имеют природную огранку, которая отчётливо проявляется иногда на микроуровне, например, у маленьких крупиц сахара, соли и т. д. У естествоиспытателей была уверенность в том, что природная огранка в кристалле обусловлена его внутренней структурой.
Знание структуры вещества важно, поскольку его свойства определяются не только химическим составом, но и тем, как расположены атомы (молекулы). Известный пример — графит и алмаз. Химически они одинаковы: оба являются формами углерода. Однако структуры этих углеродных форм совершенно различны и, в частности, имеют разные кристаллографические группы. Как следствие, эти материалы обладают различными физическими свойствами: один из них — исключительно мягкий, другой, наоборот, исключительно твёрдый, один — матово-чёрного цвета, другой — прозрачный и т. д.
Наука, изучающая строение кристаллов и вопросы кристаллообразования, называется кристаллографией. После открытия квазикристаллов появился раздел, посвящённый изучению этих новых структур.
Слово кристалл происходит от древнегреческого κρύσταλλος, которое означает «лёд», «горный лёд» или «горный хрусталь».
Отдельные элементы науки, которые в какой‐то степени можно отнести к кристаллографии, усматриваются ещё в работах древних греков (правильные многогранники). Появившийся в самом начале XVII века (1611 год) трактат И. Кеплера «О шестиугольных снежинках» рассматривается как наиболее ранний предшественник литературы по структурной кристаллографии. Только в конце XVIII века было сформулировано важнейшее положение кристаллографии о «плоскостях спайности», высказанное выдающимся французским учёным Р. Ж. Гаюи. История этого открытия подобна легенде о «ньютоновом яблоке». Кристалл кальцита при нечаянном падении из рук Гаюи разбился на многочисленные ромбоэдрические осколки. Это натолкнуло на мысль, что кристалл может раскалываться лишь вдоль плоскостей, направления которых предопределяются данным кристаллом. Дальнейшее измельчение осколков показало, что кристалл состоит из параллелепипедов и многогранников таких форм, что из них также можно сложить параллелепипеды.
Из представления о параллелепипедальном устройстве кристаллов — как множества параллелепипедов, приставленных друг к другу — выросла теория кристаллических решёток. Создателем этой теории был один из крупнейших кристаллографов О. Браве.
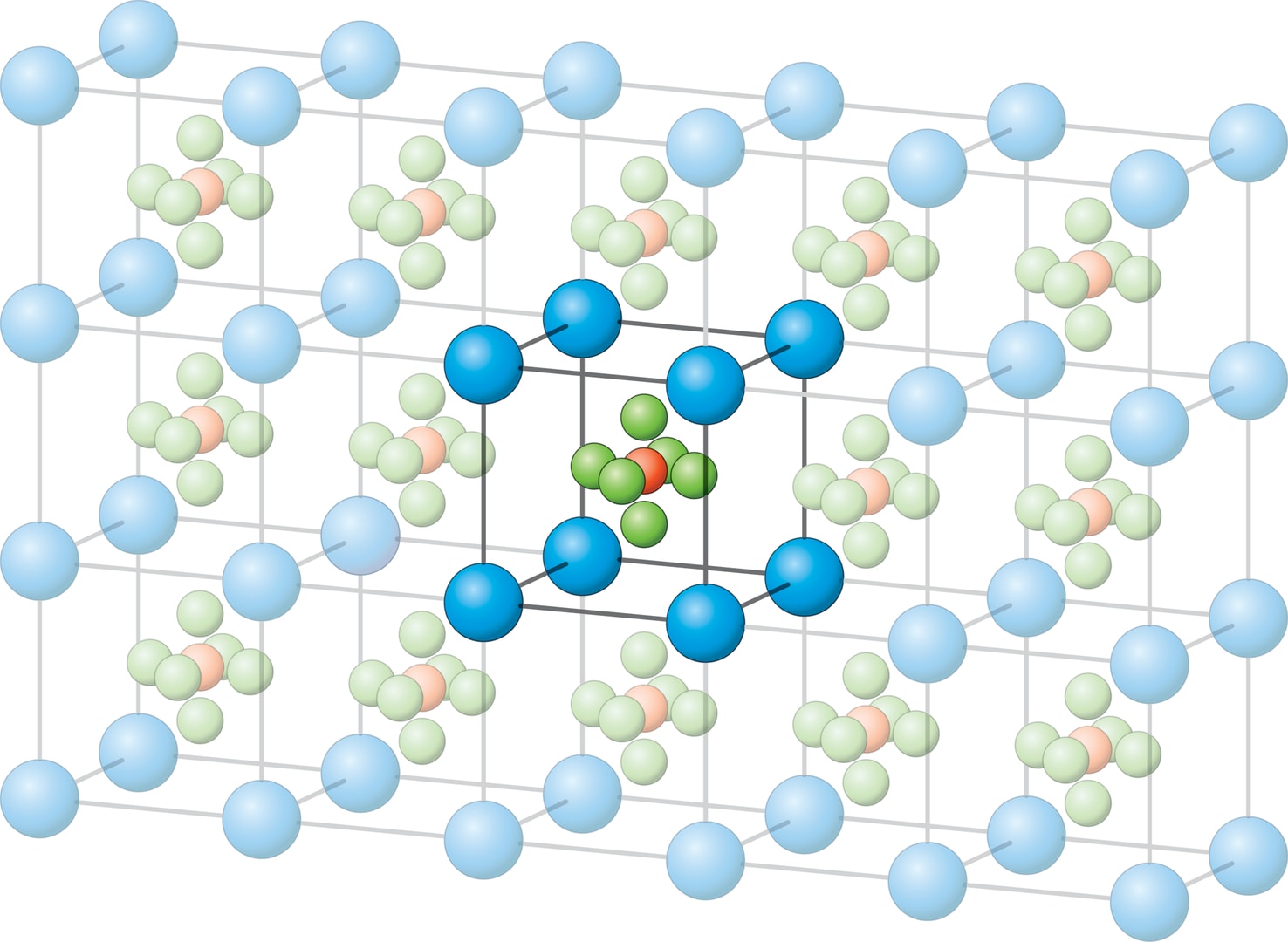
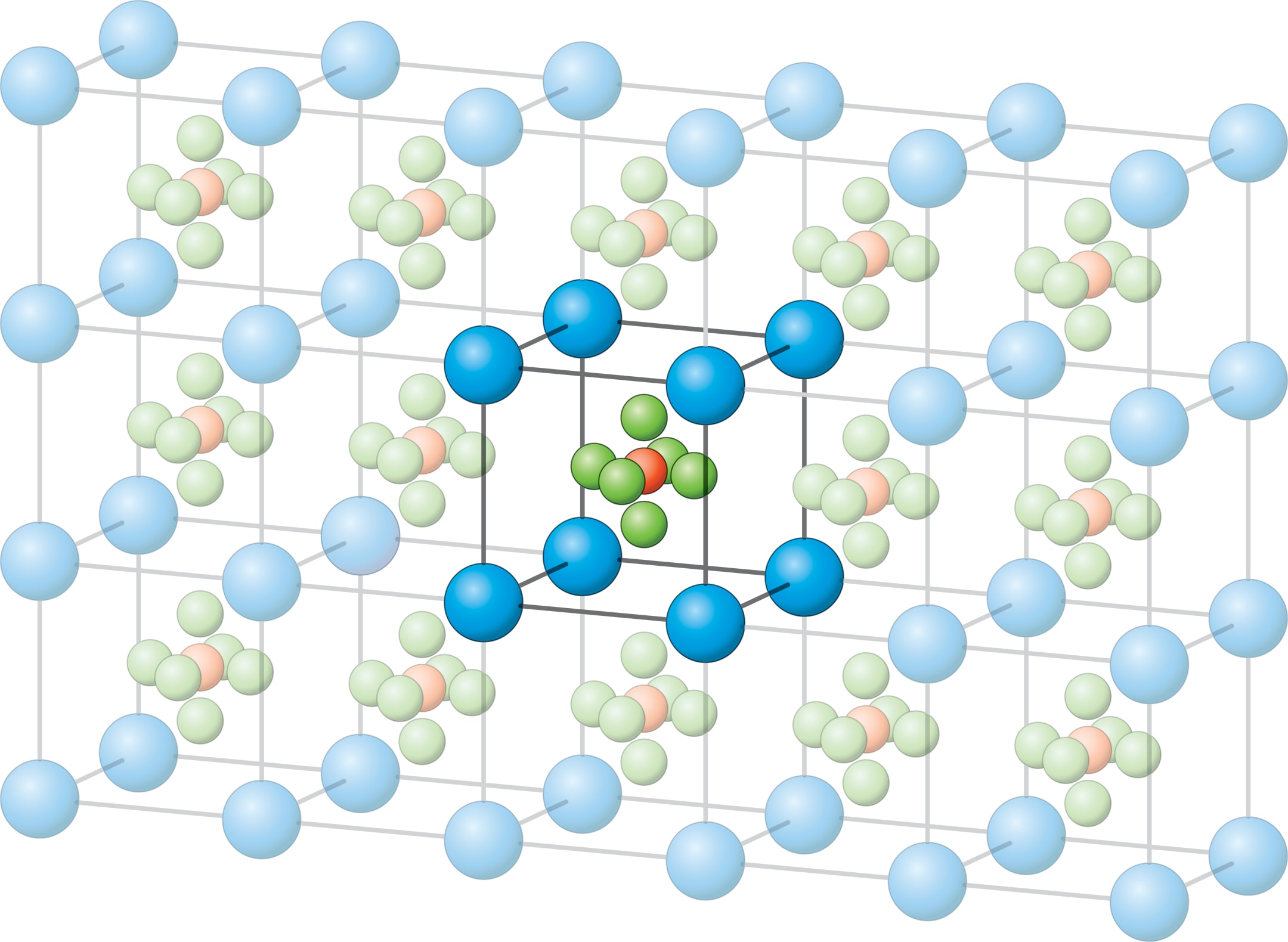
Построим на трёх некомпланарных (не лежащих в одной плоскости) векторах ${a}$, ${b}$, ${c}$ параллелепипед и разнесём его при помощи трансляций (сдвигов) на векторы $p{a} + q{b}+ r{c},$ где коэффициенты $p$, $q$, $r$ — целые числа. Решётка — это множество вершин так полученных параллелепипедов. Если в исходный параллелепипед поместить несколько точек, представляющих собой атомы вещества, то при рассмотренном «тиражировании» получим семейство нескольких параллельно ориентированных решёток. Это объединение одинаковых параллельно расположенных решёток и есть математическая модель кристалла, появившаяся в первой половине XIX века и в целом «работающая» до сих пор. Периодичность внутренней структуры кристалла в трёх линейно независимых направлениях является основным положением кристаллографии.
Центральной математической идеей всей кристаллографии является симметрия кристалла. Симметрией той или иной фигуры называется движение пространства, совмещающее фигуру с собой. Множество всех симметрий любой фигуры обладает тремя характерными свойствами:
1) произведение двух симметрий $g_1\cdot g_2$ как результат их последовательного выполнения также является симметрией фигуры;
2) так называемое тождественное движение, которое оставляет на месте любую точку пространства, а значит, оставляет неподвижной и любую фигуру, также можно рассматривать как симметрию фигуры (собственно говоря, тождественное движение — это не движение, а «стояние» на месте);
3) наряду с симметрией $g$ обратное ей движение $g^{-1}$, возвращающее каждую точку пространства на прежнее место, также является симметрией фигуры.
Множество движений с этими тремя свойствами называют группой симметрий.
Если взять точку $x$ пространства и разнести её всеми движениями из какой‐то группы симметрий $G$, то получится множество точек, которое называется орбитой $x\cdot G$ точки $x$ относительно группы $G$.
Например, группа симметрий квадрата состоит из восьми элементов: четырёх вращений, включая тождественное, и отражений относительно четырёх прямых. И орбита точки может состоять, в зависимости от выбора этой точки, из восьми, четырёх или одной-единственной точки (последнее — в случае, если эта точка — центр квадрата).
Наряду с группой всех симметрий данной фигуры рассматривают и неполные группы данной фигуры, т. е. такие подмножества симметрий полной группы, для которых выполняются условия 1)—3).
Рассмотрим произвольную решётку, одна точка которой совпадает с началом координат. Группа движений пространства, которая сохраняет начало координат и при этом совмещает решётку с собой, называется кристаллическим классом (точечной кристаллографической группой). Ещё до Браве были найдены все 32 кристаллических класса (И. Ф. Гессель, 1830 год). Очень важно, что в кристаллическом классе среди вращений могут быть оси второго порядка (поворот на 180°), третьего порядка (поворот на 120°), четвёртого (на 90°) и шестого порядка, но невозможна ось пятого порядка.
Кристаллический класс, являющийся для некоторой решётки её полной точечной группой, называется голоэдрией решётки. Среди 32 кристаллических классов имеется лишь 7 голоэдрий. Самая «бедная» голоэдрия — триклинная, она состоит из двух элементов: тождественного преобразования и симметрии относительно точки решётки (такой симметрией обладает любая решётка). Более богатые голоэдрии — моноклинная, ортогональная, квадратная, ромбоэдрическая, кубическая, гексагональная — присущи не всем, а лишь специальным решёткам. Браве обнаружил, что за исключением решёток с гексагональной голоэдрией, во всех остальных решётках можно найти параллелепипед решётки (вообще говоря, отличный от основного, по которому строилась решётка), группа симметрий которого есть голоэдрия решётки. Для каждой решётки такого типа параллелепипед минимального объёма называют параллелепипедом Браве. Для гексагональной голоэдрии (совпадающей с полной группой правильной шестиугольной призмы) параллелепипед Браве определяется особо. Браве нашёл параллелепипеды для всех решёток. Существенно различных типов оказалось 14. Соответственно, решётки также распределились по 14 типам Браве.
Классификация Браве стала основой для описания самых общих групп симметрий кристаллов — так называемых кристаллографических групп.
Группа движений пространства называется кристаллографической, если орбита любой его точки является дискретным множеством, т. е. таким, в котором точки отделены друг от друга. Кроме того, орбита относительно такой группы, по предположению, не должна иметь сколь угодно больших полостей: где бы ни был расположен шар достаточно большого фиксированного радиуса, он должен содержать хотя бы одну точку из данной орбиты.
Пример простейшей кристаллографической группы — это группа $G$, порождённая тремя сдвигами на некомпланарные векторы ${a}$, ${b}$, ${c}$. Эта, так называемая первая триклинная, группа состоит из трансляций пространства на векторы решётки $p{a} + q{b}+ r{c}$. Очевидно, что орбита $x\cdot G$ любой точки $x$ из решётки есть сама эта решётка. Таким образом, первая триклинная группа является группой симметрий решётки. Если точка $x$ не принадлежит решётке, то орбита $x\cdot G$ есть другая решётка, которая получается из исходной параллельным переносом. Так как орбита относительно первой триклинной группы есть дискретное множество (в нашем случае это решётка) и каждый шар достаточно большого радиуса содержит хотя бы одну точку из решётки, то группа кристаллографическая.
Помимо трансляций любая решётка обладает также и другими симметриями. Так, симметрия пространства относительно произвольной точки решётки, а также относительно произвольной «полуцелой» точки, т. е. точки вида $\frac{p}{2}{a} + \frac{q}{2}{b}+ \frac{r}{2}{c}$ являются симметриями решётки. Совокупность трансляций и симметрий относительно целых и полуцелых точек решётки образуют так называемую вторую триклинную группу. Это — следующая по сложности кристаллографическая группа. В самом плохом случае — несимметричной решётки — триклинная группа является максимальной группой симметрий решётки.
Другое дело, когда решётка обладает богатой точечной симметрией (голоэдрией). Например, у кубической решётки голоэдрия совпадает с полной группой симметрий куба, которая состоит из 48 вращений и вращений с отражениями. Поэтому в полной группе кубической решётки для каждой пары её точек $x$ и $y$ имеются 48 движений. Группа кубической решётки — ещё один пример кристаллографической группы.
Венцом развития кристаллографии в XIX веке стали исследования великого российского кристаллографа Е. С. Фёдорова (1857—1919). Он определил кристалл как дискретное множество точек (атомов), группа симметрий которого является кристаллографической группой. Другими словами, кристалл по Фёдорову есть совокупность орбит нескольких атомов относительно некоторой кристаллографической группы $G$.
Е. С. Фёдоров (одновременно с немецким математиком А. Шёнфлисом) в 1891 году нашёл все кристаллографические группы, которых оказалось 230. Этот сложный математический результат явился основой для последующего углублённого исследования строения кристаллов и их групп симметрий.
Заметим, что 229 из 230 кристаллографических групп содержат не только трансляции, но и более сложные движения с элементами вращения. Эти группы содержат симметрии решёток, и для их вывода была использована классификация, полученная Браве. Казалось, что подход Фёдорова к определению кристалла расширяет класс кристаллов, которые по Браве представляют собой объединение параллельно ориентированных решёток (совокупность орбит относительно группы одних лишь трансляций). Фёдоров был убеждён в том, что любая кристаллографическая группа, действующая в трёхмерном пространстве, содержит подгруппу, порождённую тремя трансляциями в некомпланарных направлениях. Строго это утверждение было доказано Шёнфлисом. Благодаря этому свойству кристалл по определению Фёдорова, как и раньше по Браве, есть совокупность нескольких одинаковых параллельно ориентированных решёток.
В начале XX века, благодаря выдающимся открытиям в области физики, было подтверждено основное положение кристаллографии о решётчатой структуре кристаллов. В 1912 году немецкий учёный М. Лауэ обнаружил дифракцию при рассеянии рентгеновского излучения на кристаллической решётке (Нобелевская премия, 1914 год). Опираясь на открытие Лауэ, британские физики У. Л. и У. Х. Брэгги, отец и сын, разработали основы рентгеноструктурного анализа кристаллов (Нобелевская премия, 1915 год).
Итак, согласно определению кристалла по Фёдорову, его внутренняя структура обладает богатейшей симметрией. Если красоту внешних форм кристаллов можно наблюдать непосредственно, рассматривая природные кристаллы где-нибудь на природе или в геологическом музее, то красоту их внутренней структуры, можно видеть лишь на моделях где-нибудь в академической лаборатории или на университетской кафедре. Эти столь прекрасные структуры образуются в результате кристаллизации, т. е. при переходе вещества из жидкого неупорядоченного состояния в твёрдое кристаллическое. Такой переход наступает при определённых физических условиях, например при охлаждении. Какая причина лежит в появлении глобального порядка при кристаллизации?
С точки зрения здравого смысла представлялось правдоподобным, что глобальный порядок атомной структуры кристалла есть следствие повторяемости локальных конфигураций в окрестностях атомов одного сорта. Возникновение идентичности фрагментов можно объяснить и с физической точки зрения. Американский физик Р. Фейнман писал: «Если атомы где‐то разместились так, что их расположения отвечают самой низкой энергии, то в другом месте атомы создадут такое же расположение. Если вы выберете атом ещё дальше, то ещё раз найдёте точно такие же условия. Порядок повторяется снова и снова, и конечно, во всех трёх измерениях…». Уверенность в происхождении глобального порядка из локального была, но каких-либо точных формулировок и доказательств не существовало.
Вера в «локальную причину» глобального порядка в кристаллах уступила место теоремам и доказательствам, полученным в результате исследований по локальной теории кристаллов, проведённых Б. Н. Делоне и его учениками-геометрами из Математического института имени В. А. Стеклова. В цикле работ, начатом в 70‐е годы, сотрудники МИАН доказали критерий кристаллографичности дискретного множества, нашли оценки на радиус окрестностей, идентичность которых гарантирует правильность структуры. Можно отметить также, что в локальной теории заложен подход к описанию свойств локальных фрагментов правильных систем и правил их «сборки» в глобально упорядоченную структуру.
Цикл работ по локальной теории, инициированный Борисом Николаевичем Делоне, явился достойным продолжением полувековой деятельности Делоне по развитию геометрической кристаллографии, в результате которой появились такие инструменты, как теория множеств Делоне, теория триангуляций Делоне и многое другое.
Роль найденных в локальной теории кристаллов точных условий, которые выделяют из семейства дискретных множеств именно периодические структуры, была по‐новому оценена с появлением так называемых узоров Пенроуза. В открытых британским физиком Р. Пенроузом в 1970‐е годы плоских структурах в целом периодичности нет, хотя локальные мотивы повторяются вновь и вновь.
Характерно, что в узорах Пенроуза содержится бесконечно много осей симметрии пятого порядка — прямых, вращением вокруг которых на угол 360°/5 некоторый фрагмент узора переходит в себя. Более того, в узорах Пенроуза можно найти сколь угодно большие фрагменты, обладающие пятикратной симметрией. С другой стороны, эти фрагменты (за исключением, быть может, одного) должны быть ограниченными. Позже математики показали, что структуры с аналогичными свойствами существуют и в трёхмерном пространстве.
То, что подобные структуры не могут представлять кристалл, следовало из свойства, известного кристаллографам ещё в XIX веке: у периодических структур не может быть оси симметрии пятого порядка.
Возникло новое направление исследований в геометрии — квазикристаллические структуры. Но вопрос о том, есть ли «реальные» квазикристаллы, оставался открытым.
В 1982 году в лаборатории израильского физика Д. Шехтмана был получен сплав алюминия и марганца, структура которого имела отчётливую осевую симметрию пятого порядка… Через три десятилетия это открытие было отмечено Нобелевской премией по химии «за открытие квазикристаллов».
В заключение отметим, что в последнее время ведутся интенсивные исследования по вопросам теоретического конструирования новых материалов, в области предсказания новых структур с предписанными характеристиками. Данное направление обещает создание материалов с новыми удивительными свойствами. И ключевым инструментом этих исследований являются геометрические методы.