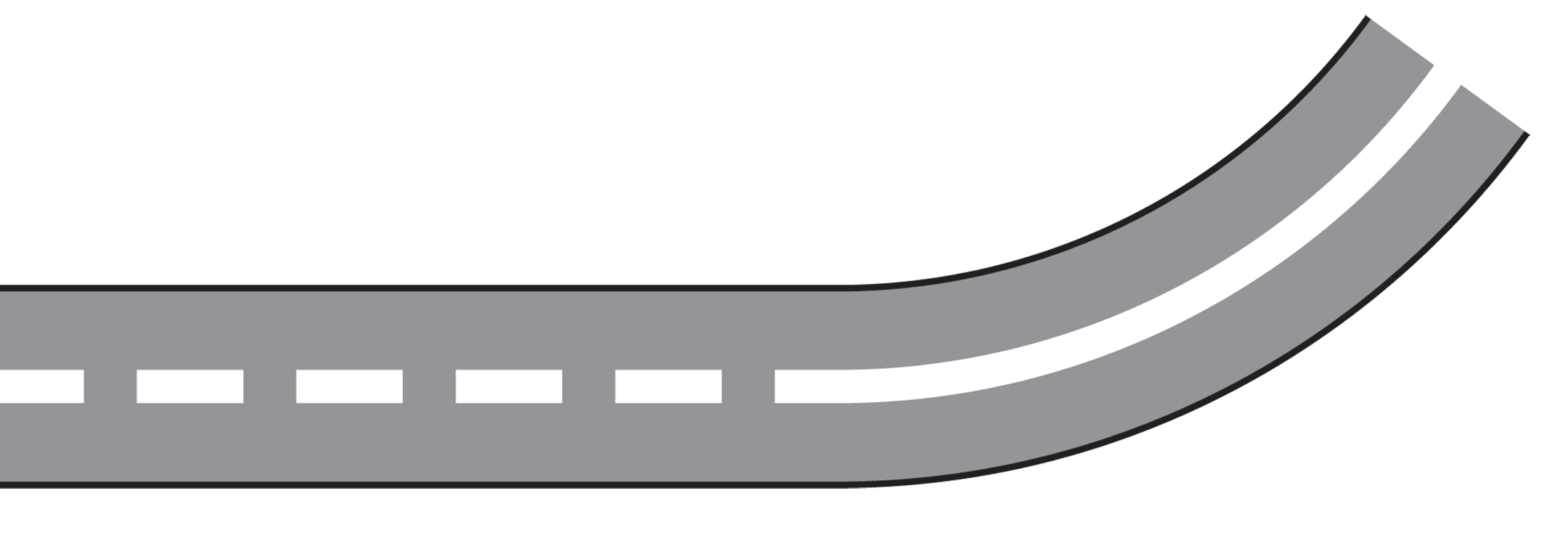
Прохождение поворота на трассе — демонстрация мастерства пилота в «Формуле‐1». Но с этой задачей ежедневно сталкиваются и рядовые водители, и машинисты поездов. А можно ли проектировать дороги так, чтобы уменьшить «стрессы» на поворотах для водителей, пассажиров и даже для техники?
Очевидно, что дорога должна быть гладкой, без изломов. Но для скоростных трасс этого недостаточно.
Представим дорогу в виде прямой, переходящей в дугу окружности. На прямолинейном участке во время движения руль не повёрнут. При въезде на участок дуги окружности его необходимо резко повернуть. Пассажиры почувствуют толчок. Понятно, что описанный «толчок» при вхождении в такой поворот испытывает и техника. Но если водитель автомашины ещё может попытаться «сгладить» ситуацию за счёт выбора траектории, то машинист поезда такого выбора не имеет, и при неудачной геометрии полотна страдать будут все — от пассажиров до рельсов (последние будут быстро изнашиваться).
Итак, непосредственная склейка прямой и окружности в данной ситуации — решение не лучшее. Возникает задача расчёта переходной кривой — части дороги, осуществляющей «плавный» переход с прямолинейного участка на дугу окружности постоянного радиуса.
В математике у кривых есть важная характеристика — кривизна. У окружности радиуса $R$ кривизна равна $1/R$, у прямой кривизна равна $0$. Для произвольной гладкой кривой на плоскости кривизна в заданной точке определяется с помощью соприкасающейся окружности, дуга которой в окрестности точки «похожа» на дугу кривой.
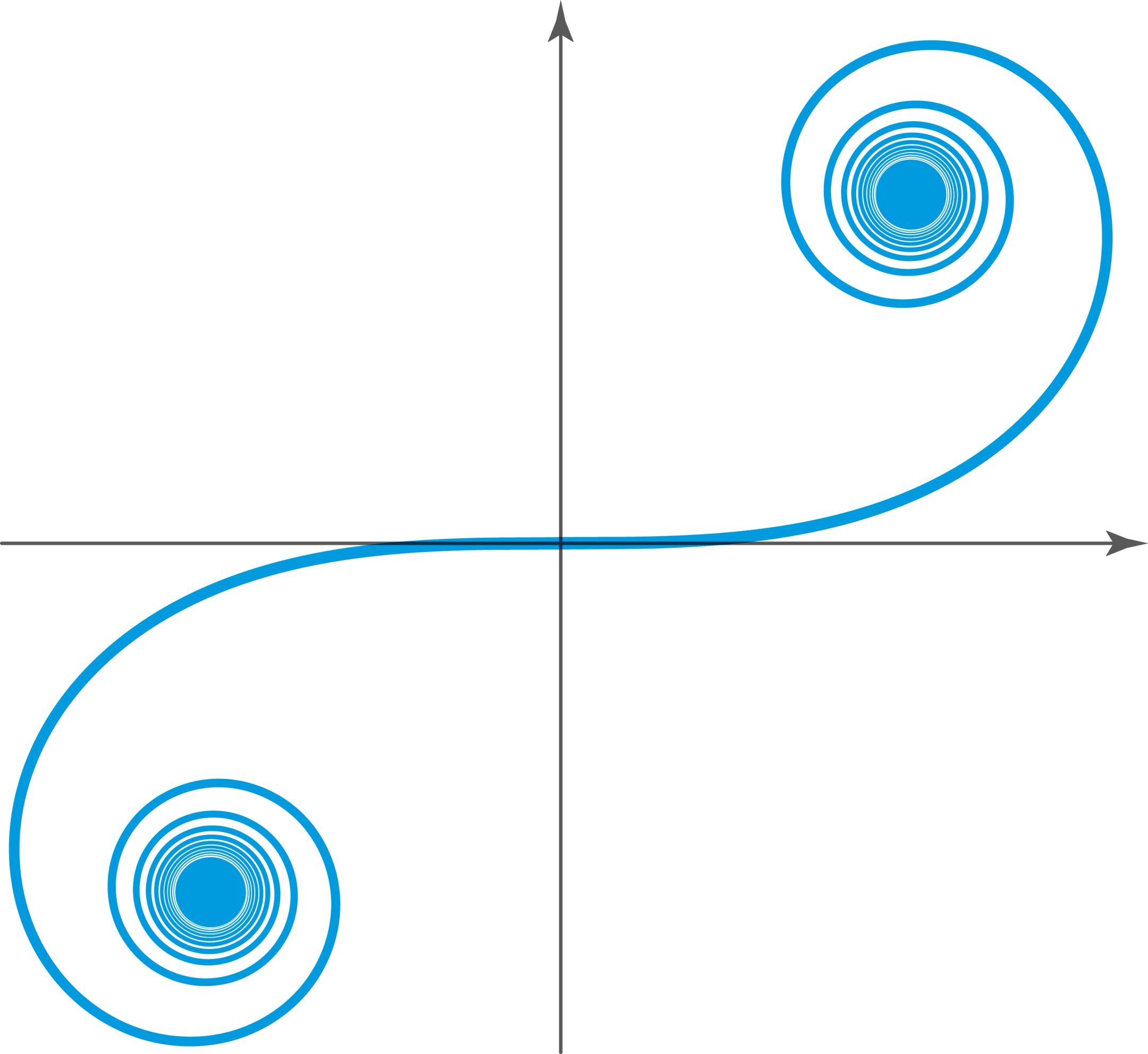
Можно ли найти такую переходную кривую, чтобы её кривизна менялась линейно в зависимости от пройденного пути? Тогда при движении с постоянной (по мо дулю) скоростью руль автомобиля нужно было бы поворачивать равномерно.
Такие кривые существуют, они называются спиралями Корню или клотоидами. Для расчётов спирали Корню сложны, но в построении переходных кривых служат важной отправной точкой.
Инженеру-строителю непросто рассчитать параметры дороги в форме клотоиды — это сложная вычислительная задача. Кроме того, приходится учитывать всевозможные внешние обстоятельства. Например, это могут быть ограничения на длину переходного участка (с прямолинейного отрезка на дугу окружности). Поэтому на практике, и в автодорожном деле, и при сооружении железных дорог, часто используют кубическую параболу, хорошо приближающую клотоиду ($y=ax^3$ — пример кубической параболы).
Замечательные кривые находят множество применений. Клотоида, «герой» поворотов автодорог, впервые была рассмотрена Якобом Бернулли в связи с задачей о форме упругой пластины. Позднее кривую изучал Эйлер, так что часто её называют спиралью Эйлера. А ещё клотоида называется спиралью Корню, в честь французского физика, использовавшего её для решения задач физической оптики. Относительно недавно эта кривая даже стала гвоздём аттракциона: в 1970‐е годы в Германии сконструировали американские горки с мёртвой петлёй, часть которой — дуга клотоиды. В отличие от прежних конструкций здесь решена проблема безопасности: посетители не рискуют получить травму, что объясняется гладкостью прохождения виражей.