Удивительный мир дикой природы иногда дарит натуралистам сюжеты, в которых явно просматриваются математические закономерности. В одних случаях эти закономерности удаётся объяснить на основе имеющихся знаний, получить их как вывод в логической цепочке рассуждений. А бывает и так, что подобный рациональный путь найти не удаётся, и тогда доказательства уступают место гипотезам.
Разберём пример из жизни насекомых, демонстрирующий, что источником гипотез могут стать математические свойства величин в наблюдаемых закономерностях. Речь пойдёт о живущих в Северной Америке цикадах, называемых периодическими. У части видов рода жизненный цикл — 13 лет, у другой части — 17 лет. Раз в 13 лет на поверхность из подземного мира выходят личинки одного типа, раз в 17 лет — другого (периодичность). Основное предположение в объяснении цифровой загадочности циклов — то, что в борьбе за выживание рода цикады «научились» использовать свойства… натуральных чисел!
Есть две гипотезы, дополняющие друг друга и объясняющие возникновение видов цикад‐13 и цикад‐17. Математическая составляющая в обеих гипотезах одна — простота чисел 13 и 17. Напомним: простые числа — те, которые нельзя представить в виде произведения двух меньших. Ключевое утверждение: если $p$ — простое число, а $n<p$, то наименьшее общее кратное чисел $n$ и $p$ равно произведению $np$.
Первая гипотеза объясняет, как числа 13 и 17 «защищают» цикад от хищных врагов. Например, если в какой‐то год появились и цикады‐17, и хищники, у которых длина жизненного цикла $n<17$, то следующая «встреча» состоится только через $17n$ лет (наименьшее общее кратное чисел $n$ и 17). Хищники не смогут ждать так долго… А подобрать мутацию вида хищников так, чтобы длина цикла была равна 17, — сложная задача даже для «естественного отбора».
С цикадами‐13 ситуация сходная. Общее важное свойство — числа 13 и 17 не только простые, но и большие, что делает встречи с хищниками редкими, разнесёнными по времени.
Вторая гипотеза анализирует возможность гибридизации цикад‐13 и цикад‐17, которая опасна и нежелательна, так как может разрушить имеющуюся цикличность. Спасает то, что пересечения происходят только раз в 221 год.
Простые числа в современных европейских языках (германских и романских) называются primes, что происходит от их наименования у Евклида — protos (первый, начальный). А в русском языке появляется слово «простое», добавляющее оттенок неразложимости, цельности — в духе основной теоремы арифметики.
Греческий учёный Эратосфен в III веке до н. э. придумал способ, алгоритм нахождения всех простых чисел, не превосходящих некоторого фиксированного числа $N$. Выпишем все натуральные числа от 2 до $N$. Вычеркнем в списке все числа, кратные 2 (кроме самой двойки); наименьшее невычеркнутое число после 2 — это 3, следующее простое число. Оставляем тройку и вычёркиваем числа, кратные 3, и т. д. Если такие действия проделать для всех чисел, не превосходящих $\sqrt{N}$, то незачёркнутыми останутся все простые числа и только они.
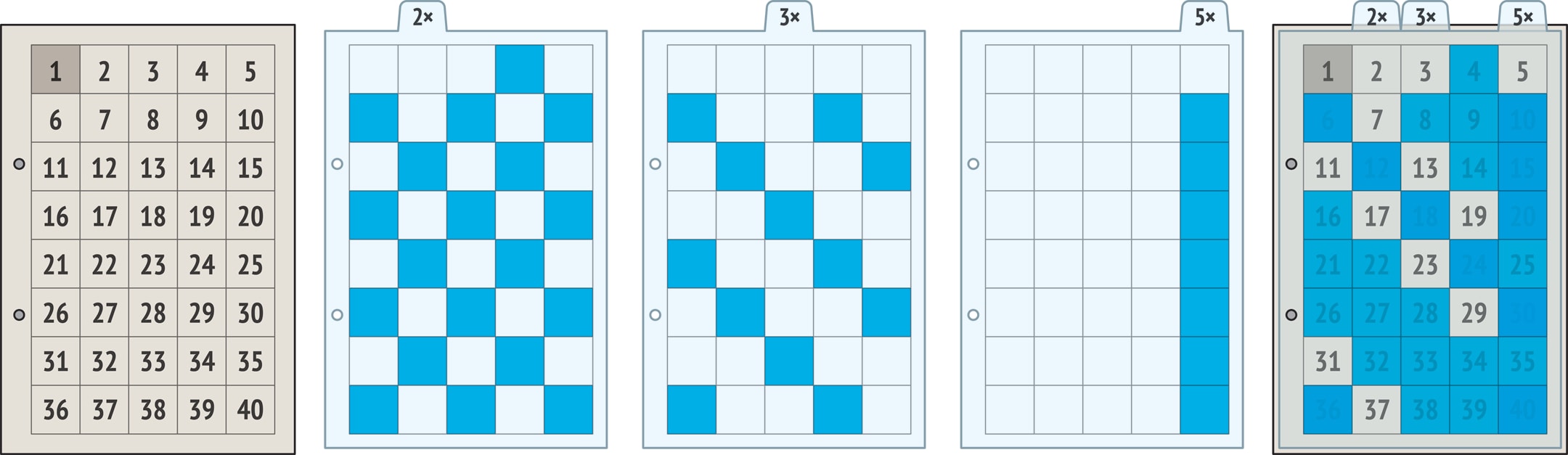
Описанный процесс можно механизировать, сделать наглядным. Напечатайте на листе бумаги числа от 1 до $N=nm$ в виде таблицы размера $n\times m$. На первой прозрачке на местах чётных чисел (кроме 2) напечатайте закрашенные области. На второй — то же с числами, кратными 3 (кроме самой тройки), и т. д. Если создать достаточно большой набор таких прозрачек, то при наложении их на основную таблицу все простые числа будут видны (пройдут через сито, решето отбора), а все составные — скрыты.
На каждом листе-прозрачке закрашенные клетки будут встречаться через одинаковое число шагов, а вот вид и расположение образуемых ими линий зависят от количества столбцов в таблице.
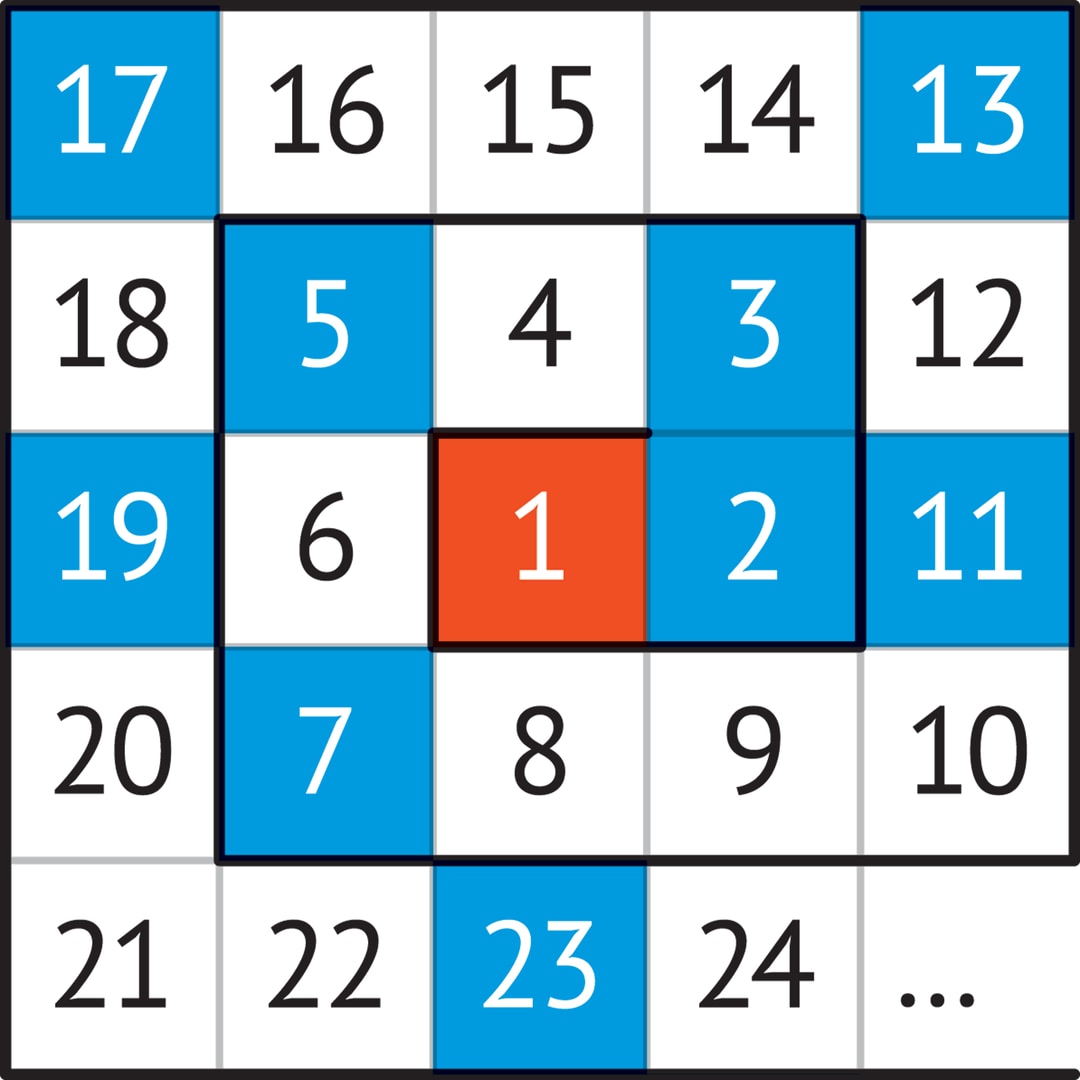
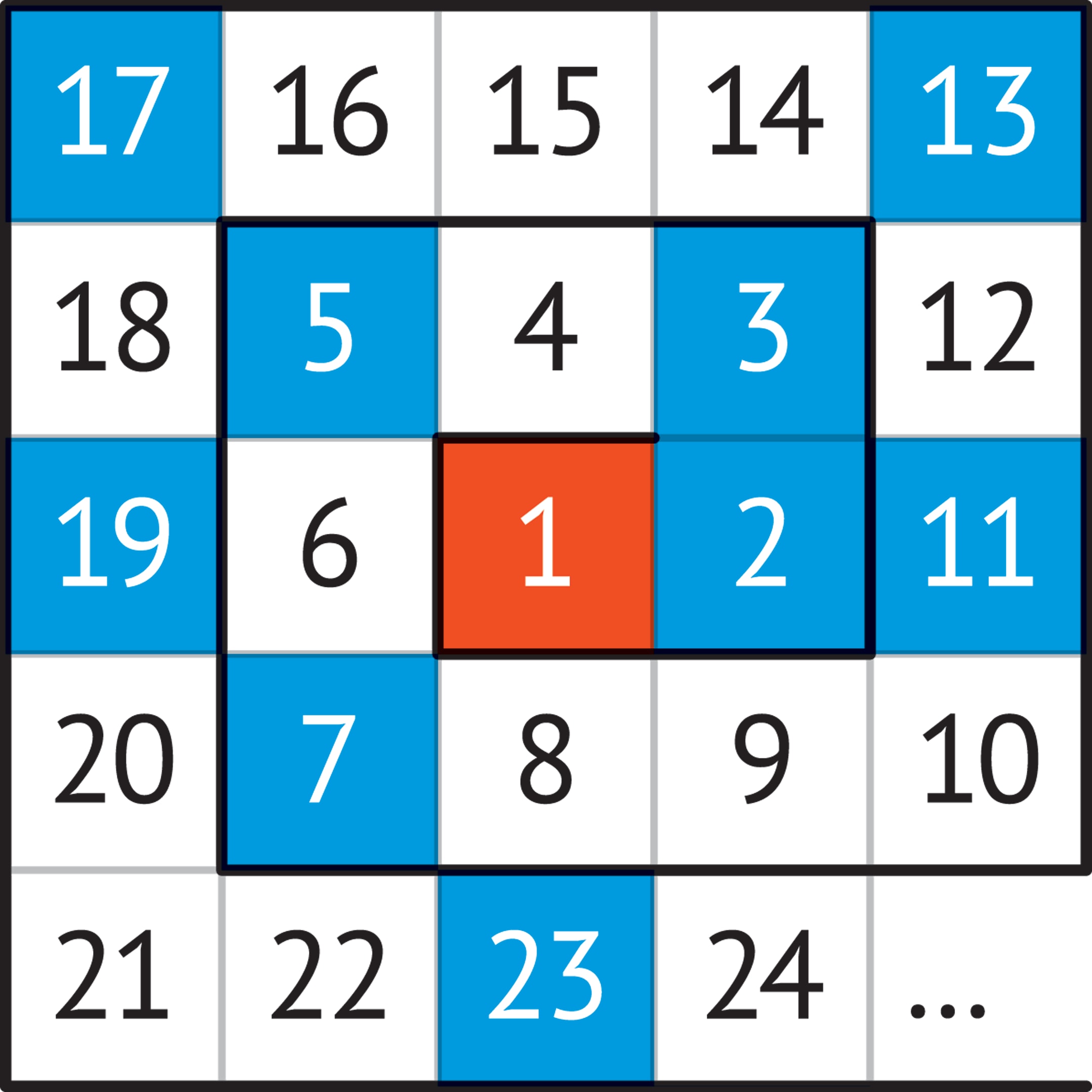
Скатерть Улама — попытка придать множеству простых чисел геометрический облик.
Возьмём клетчатый лист и занумеруем все клетки по спирали: какой-то центральной клетке дадим номер 1, клетке справа — 2, клетке над ней — 3 и т. д., двигаясь вокруг клетки «1». Если закрасить клетки, номера которых — простые числа, то получится затейливый точечный узор, который и называется скатертью Улама, в честь впервые нарисовавшего его математика Станислава Улама.
Бросается в глаза, что часть точек выстраивается в линии двух типов, параллельно диагоналям «скатерти».
Множество простых чисел устроено замысловато, но можно описать его «в целом»: указать многочлен с целыми коэффициентами от многих переменных, множество всех положительных значений которого при натуральных значениях переменных есть в точности множество всех простых чисел. Первые такие многочлены были построены в начале 1970‐х годов, на сегодняшний день минимальное количество переменных — 10 (результаты Ю. В. Матиясевича, одного из авторов этой книги).