Чем объясняется повышенная точность результатов измерения штангенциркулем в сравнении с измерениями при помощи обычной линейки? На первый взгляд — всё дело в точной фиксации объекта, но больший вклад вносит математическая составляющая конструкции штангенциркуля.
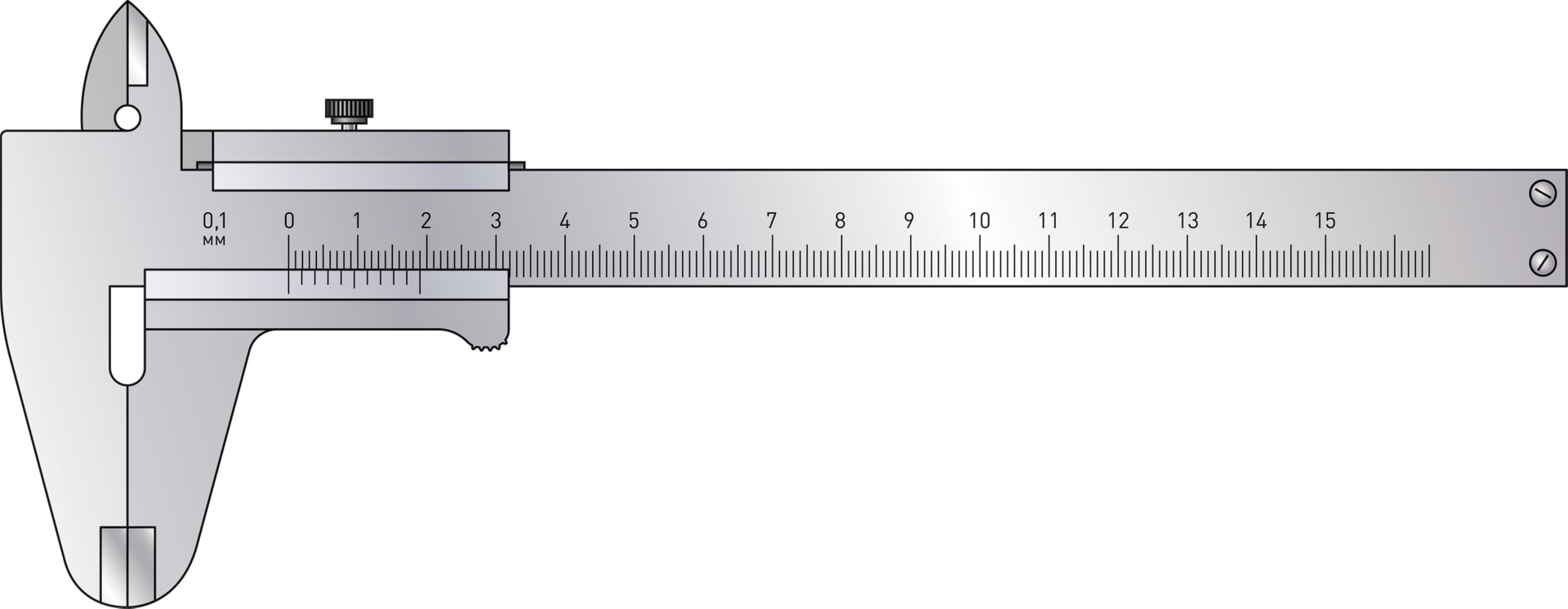
Основное отличие от обычной линейки — дополнительная шкала на подвижной рамке. Если бы на подвижной рамке вместо набора делений была лишь одна риска, то по сути штангенциркуль был бы обычной линейной, а риска — служила бы указателем-«курсором». При измерении объекта риска, показывающая сдвиг рамки относительно штанги, может попасть между делениями основной шкалы, и размер можно будет определить только с точностью до миллиметра, округлив результат либо в меньшую, либо в большую сторону.
Идея, не усложняющая устройство, но позволяющая получать более точные результаты измерения, появилась несколько веков назад. Она заключается в нанесении на подвижную рамку специальной дополнительной шкалы — нониуса.
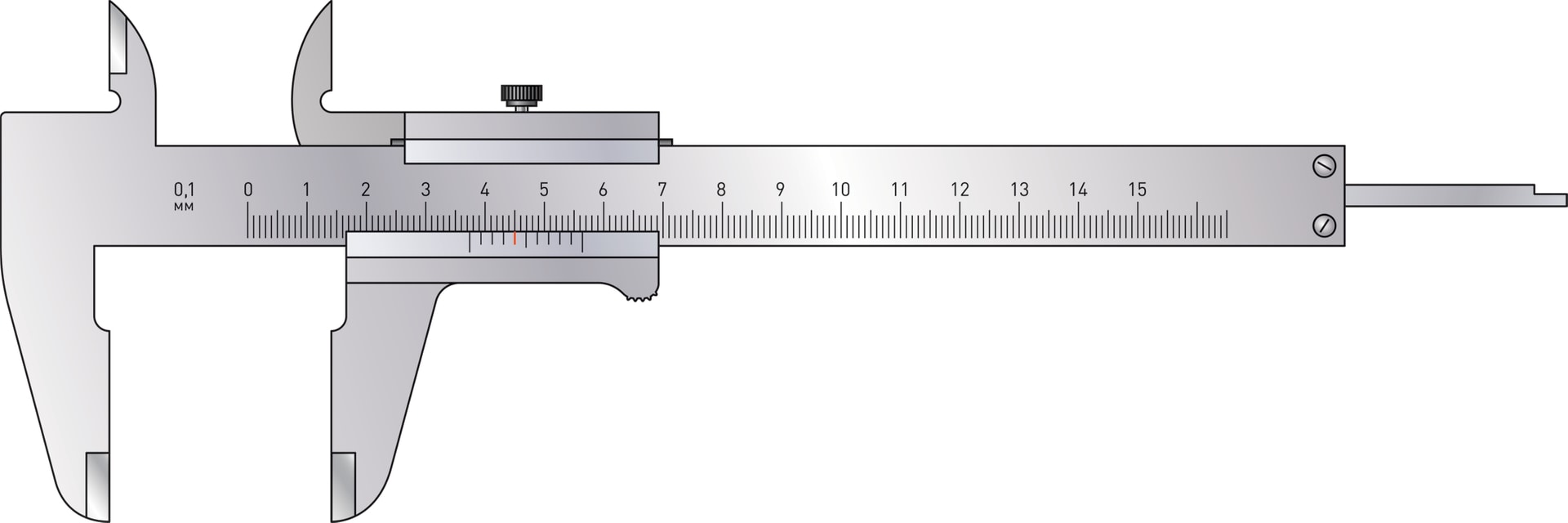
Десять делений шкалы на подвижной рамке по длине совпадают с 19 делениями основной шкалы, расположенной на штанге. Шкала, построенная по такому принципу, и называется нониус — в честь португальского математика П. Нуниша (латинизированное имя — Nonius), придумавшего сам принцип. Современный вид такой шкалы был предложен французским математиком П. Вернье, и поэтому второе название — верньер.
Удивительным образом эта простая конструкция увеличивает точность результатов измерений на порядок — до $0{,}1$ мм!
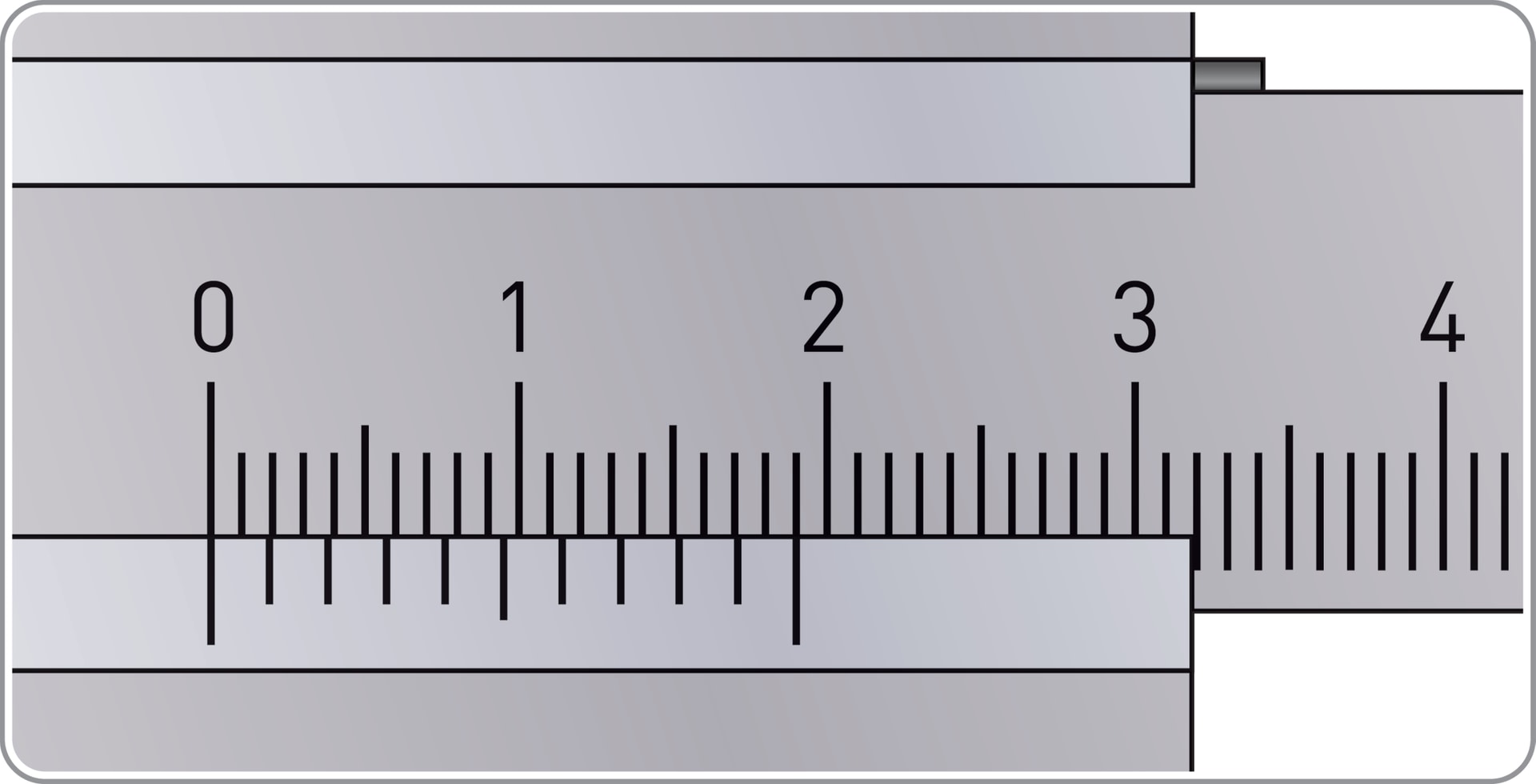
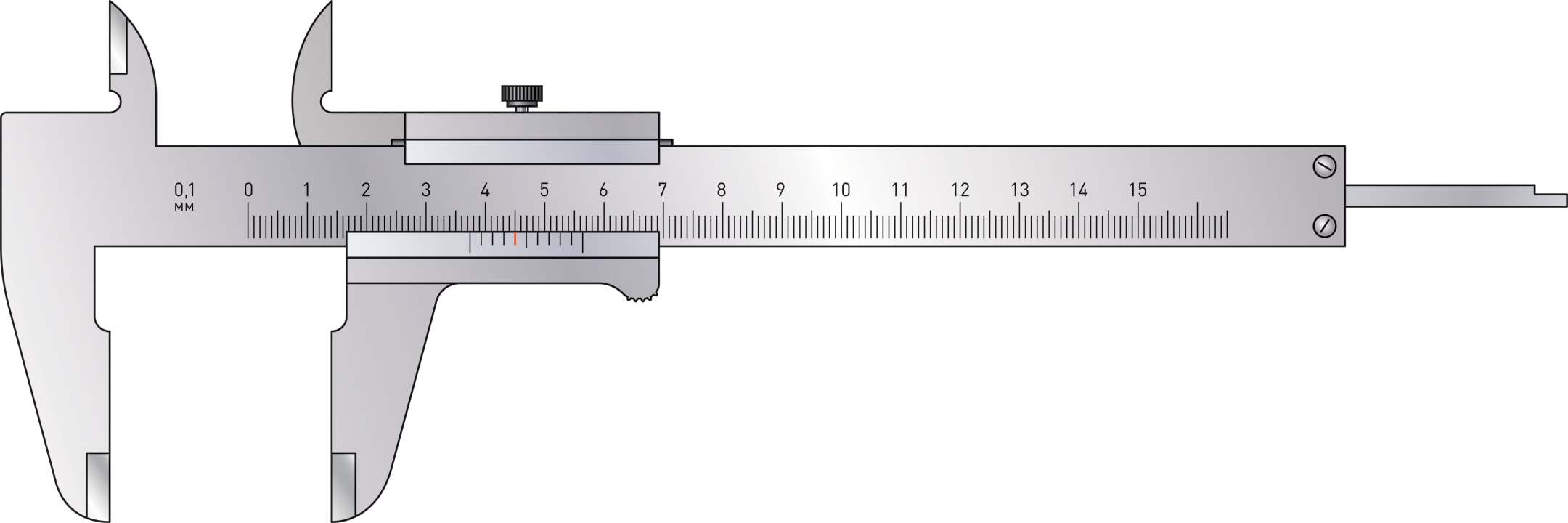
В изображённом на рисунке случае нулевая риска дополнительной шкалы указывает на основной шкале размеры детали: больше 37 мм, но меньше 38 мм. Обозначим размер детали (показатель риски) через $37+x$.
Будем двигаться по делениям дополнительной шкалы слева направо и найдём то деление, которое совпадает (или почти совпадает) с каким-нибудь делением основной шкалы. Допустим, деление $k$ дополнительной шкалы совпало (почти совпало) с делением $l$ основной шкалы (где $l$ считается от отметки 37).
Из совпадения делений основной и дополнительной шкал получаем уравнение $$ 37+l≈ 37+x+k\cdot\frac{19}{10}. $$
Поскольку на два деления основной шкалы приходится приблизительно одно деление подвижной, а $k$ и $l$ — целые числа, то $l=2k$.
Отсюда $x≈ k \cdot 0{,}1 $.
В изображённом на рисунке случае $k=4$. Значит, размер детали примерно равен $37+4\cdot 0{,}1=37{,}4$ (мм).
Бросается в глаза, что в уравнении у числа 37 — роль статиста: оно сразу сокращается. Если в общем случае обозначить размеры детали в миллиметрах через $N+x$, где $N$ — целое число, $0\le x<1$, то вывод будет тот же: $x≈ k\cdot 0{,}1$, размер детали приближённо равен $N+k\cdot 0{,}1$ (мм).
Из последней формулы видно, что $0{,}1$ — шаг в этой записи — точность получаемого результата. Эта величина — следствие соотношений между делениями дополнительной шкалы и основной шкалы. Например, при пропорции $10:9$ (а не $10:19$, как в примере), точность не изменится ($0{,}1$ мм), но считывать данные будет труднее из-за мелкого шага нониуса. А вот при пропорции $20:39$ (встречается в штангенциркулях) точность возрастает до $0{,}05$ мм!
Дополнительная шкала как источник дополнительной точности применяется и в других измерительных инструментах.