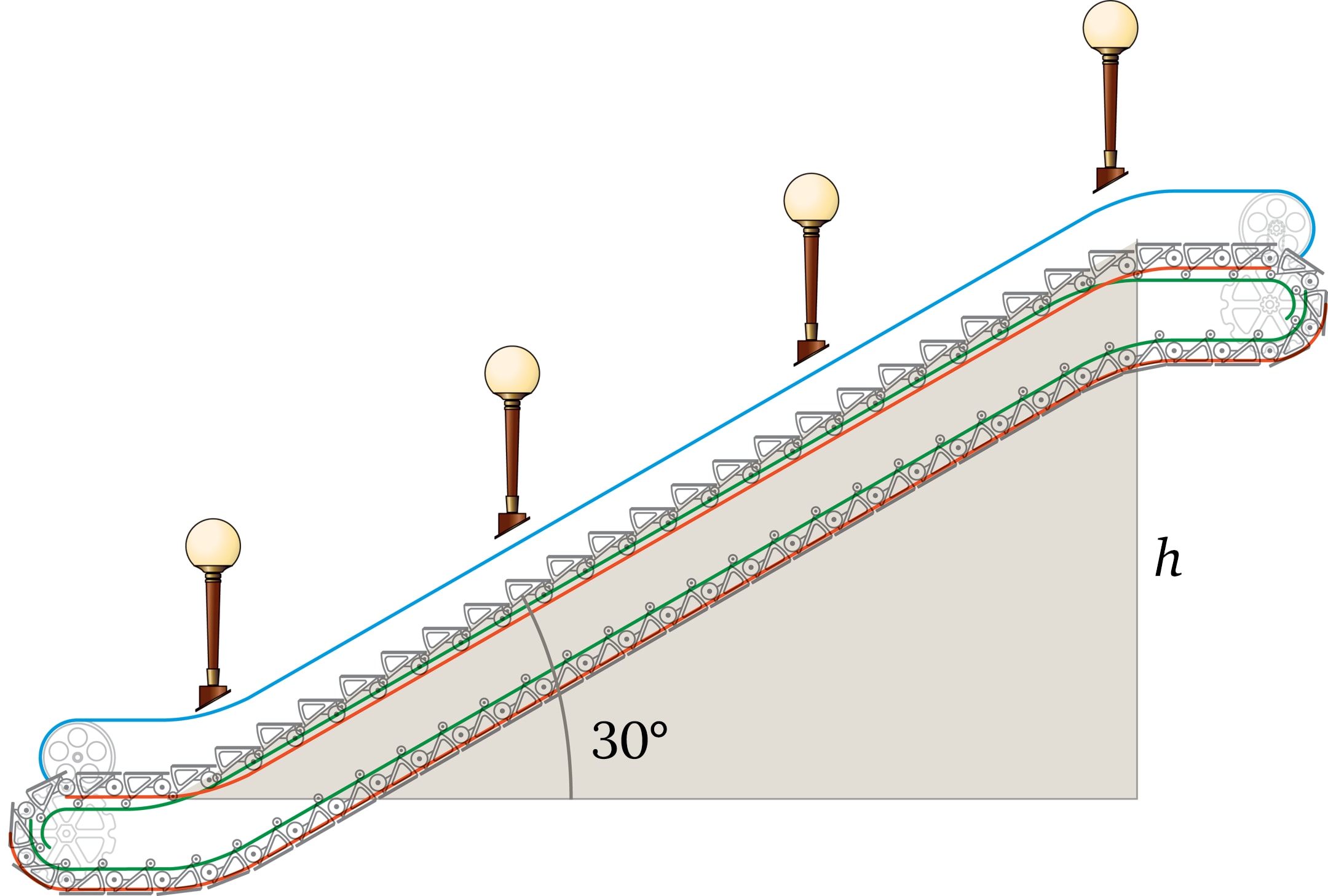
Как оценить глубину заложения станции метро, на которую вы спускаетесь по эскалатору?
Все российские эскалаторы, с самых первых моделей и до производимых в наше время, имеют угол наклона в 30 градусов.
Достроим мысленно эскалатор до естественного прямоугольного треугольника. Длина его гипотенузы — это длина эскалатора, а длина меньшего из катетов будет примерно равна глубине заложения той станции метро, на которую ведёт этот эскалатор.
Как посчитать длину эскалатора, спускаясь по нему? Можно засечь время, но тогда для вычисления пути нужно точно знать скорость движения, а она меняется в пределах от $0{,}75$ м/c до $1$ м/c (в зависимости от типа эскалатора).
Другой возможный способ решения — измерить длину эскалатора в ступеньках. Размеры одной ступеньки найти нетрудно. Но сосчитать число ступенек, находясь на движущемся полотне эскалатора, не так‐то просто…
Что ещё можно придумать? Спускаясь или поднимаясь по эскалатору, мы проезжаем вдоль ряда ламп, расположенных на равных расстояниях друг от друга. Нормативами задаётся освещённость тоннеля, исходя из которой устанавливается и расстояние между соседними лампами. Оно составляет примерно 5 метров, но его несложно измерить и самому.
Пусть $s$ — расстояние между лампами, $n$ — число ламп, тогда длина эскалатора равна $(n-1)s$, так как число промежутков между лампами равно $n-1$.
Применив известные формулы из школьной математики, находим примерную глубину заложения $$ h=(n-1) s \sin 30°=\frac{1}{2} (n-1)s. $$
Впрочем, эту формулу для $h$ можно написать и не зная «синусов» — о том, что катет, противолежащий углу в 30°, равен половине гипотенузы, школьники узнают ещё до изучения тригонометрии.
Приняв $s$ равным 5 метрам, получим простую для применения и легко запоминающуюся формулу для оценки глубины заложения станции метро.
Слово «градус» к нам пришло из латыни, а туда попало из работ вавилонских жрецов. Изучая движение Солнца, они делили его путь на 360 градусов — шагов в движении по кругу (180 днём и 180 ночью). Всё это связано и с применявшейся в Месопотамии шестидесятеричной системой. В Европе градус как научный термин появился в XVI веке.
Так что если в вашем смартфоне есть шагомер, можете называть его «градусником».