Компьютерная томография — одно из наиболее впечатляющих научных достижений ХХ века. Оно оказало революционное воздействие на всю современную медицину. За разработку компьютерной томографии А. Кормак и Г. Хаунсфилд были удостоены Нобелевской премии 1979 года в области медицины и физиологии.
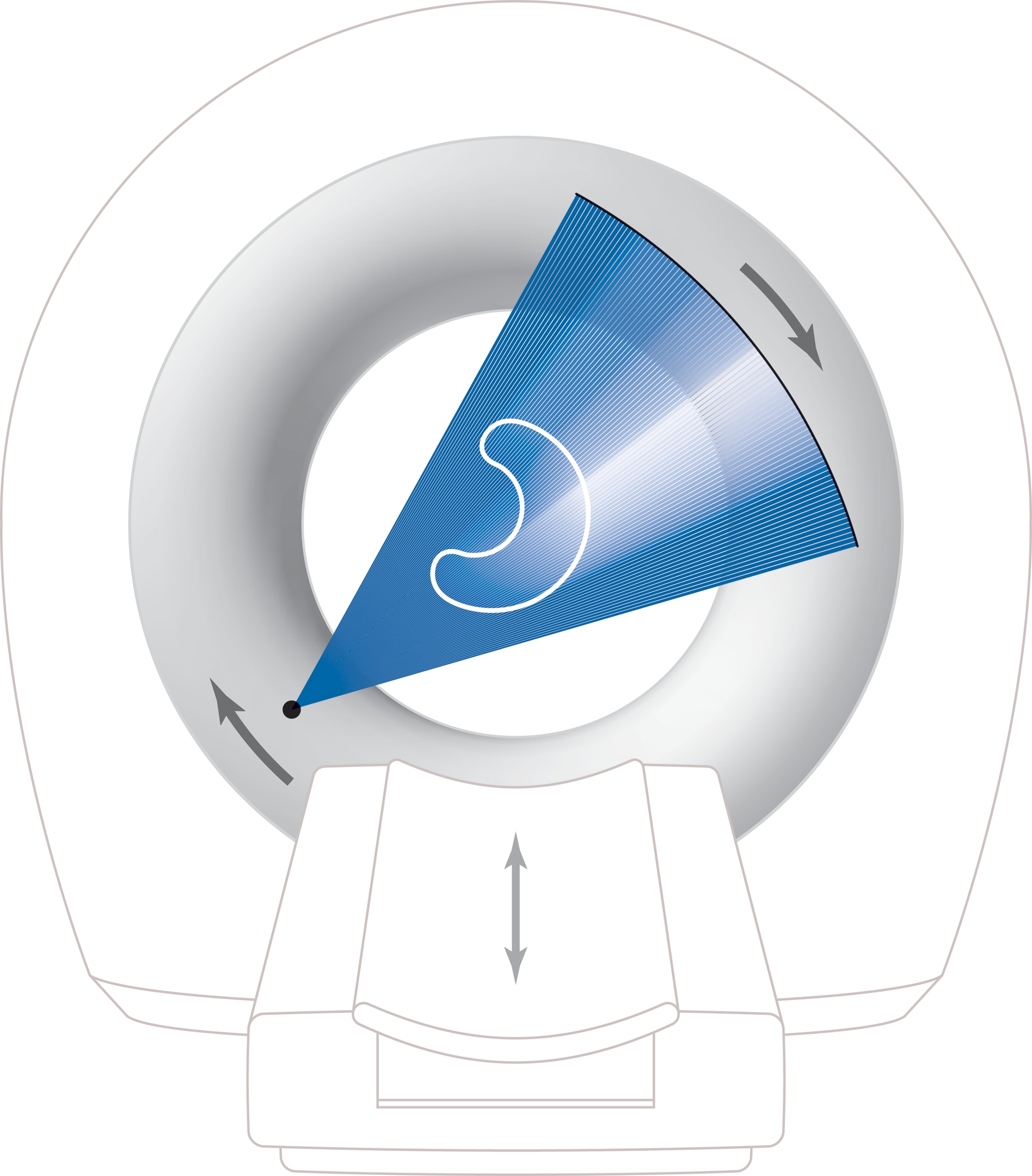
При снятии томограммы изучаемую часть тела человека микросдвигами перемещают сквозь кольцо сканирующего устройства. Сканер, состоящий из источника рентгеновского излучения и ряда детекторов, находится в корпусе, имеющем форму тора («бублика») и может вращаться в нём по кругу.
На древнегреческом τομή означает «сечение». При фиксированном относительно томографа положении тела происходит следующее. При каждом повороте сканера из источника излучения веером выходят лучи, а данные детекторов характеризуют ослабление излучения вдоль соответствующих направлений. Коэффициент поглощения в каждой точке зависит от плотности тканей организма, а интеграл от функции «коэффициент поглощения» по отрезку движения луча от источника до детектора определит суммарное поглощение луча. Если по значениям таких интегралов удастся восстановить значения интегрируемой функции, то в рассматриваемом сечении человеческий организм будет представлен картой плотности тканей. Набор изображений, полученных в серии параллельных сечений, даёт трёхмерное представление. Расположение и размеры участков с «неправильно» изменённой плотностью позволяют врачу поставить диагноз.
С математической точки зрения восстановление функции на плоскости по её интегралам вдоль всевозможных прямых — классическая задача, решённая Иоганном Радоном в 1917 году. Однако практическая реализация томографических возможностей формулы Радона стала возможной только с приходом эры компьютеров. Задача является трудной не только из‐за гигантского объёма данных, для её решения помимо компьютеров потребовались математические методы, развивавшиеся в течение всего XX столетия. Отметим, что высокая стоимость современных компьютерных томографов больше связана не с инженерной сложностью конструкций, а с зашитыми в них нетривиальными математическими алгоритмами, представляющими основную коммерческую тайну.
Современные томографы работают в режиме реального времени и отличаются высокой точностью, выявляя малейшие отличия в плотности исследуемых тканей (порядка долей процента).
Однако применение рентгеновской компьютерной томографии не всегда показано из‐за жёсткости рентгеновского излучения (например, её не рекомендуется применять для диагностирования беременных женщин). В этой ситуации приходится прибегать к менее жёсткому ультразвуковому исследованию. Ультразвук не обладает мощью рентгеновского излучения, переменная плотность тканей приводит к тому, что ультразвуковое излучение распространяется вдоль кривых линий, а не прямых. Но криволинейная задача Радона — задача о восстановлении функции на плоскости по её интегралам вдоль всевозможных кривых определённого вида, — до сих пор остаётся нерешённой. По этой причине приходится пользоваться формулой Радона для прямолинейного случая, что сказывается на точности ультразвуковых томографов по сравнению с их рентгеновскими собратьями. Усовершенствование работы ультразвуковых томографов напрямую зависит от прогресса в решении сформулированной математической задачи.
Криволинейная задача Радона имеет важное значение не только в медицине, но и, например, в геологии, где она возникает при сейсморазведке полезных ископаемых. Допустим, требуется найти рудное тело, находящееся на большой глубине. С этой целью на земной поверхности производится серия микровзрывов, эффект от которых фиксируется прилегающими сейсмическими станциями. По скорости распространения сейсмических волн можно получить данные для постановки криволинейной задачи Радона. Её решение в этом случае позволило бы локализовать разыскиваемое полезное ископаемое. Таким образом, и в случае сейсморазведки дальнейший прогресс зависит от решения криволинейной задачи Радона.
Приведено только два примера использования математических методов томографии — в медицине и геологии. На самом деле, таких применений намного больше.
Сформулированные задачи относятся к области математики, называемой интегральной геометрией. В этой науке остаётся ещё много нерешённых задач, но можно не сомневаться, что любой прогресс в их решении найдёт важные практические применения.