Популярные в XX веке кроссворды в веке XXI сменило новое увлечение — пришедшая из Японии игра судоку. Существуют различные варианты игры и множество «патентованных» рекомендаций игрокам. Удивительно, но знание математических терминов, даже только по названиям, позволяет создавать эффективные приёмы разгадывания судоку.
Задание в классическом варианте судоку — заполнить цифрами от 1 до 9 клетки квадратной таблицы $9\times 9$, которая разделена на девять квадратов $3\times 3$. В каждой строке и в каждом столбце таблицы, в каждом квадрате $3\times 3$ цифры должны быть различными.
Ряд вариантов игры получается из классического простым добавлением условий, например: «диагонали» — в каждой из двух диагоналей таблицы цифры также не должны повторяться; «неравенства» — соседние клетки таблицы связаны знаками «больше» и «меньше», которые относятся к «обитателям» этих клеток; «суммы» — вся таблица разделена не только на девять квадратов $3\times 3$, но и на области, для каждой из которых приведена сумма всех её цифр.
Начальные условия могут отличаться числом заранее «прописанных» цифр. Как правило, уменьшение числа начальных цифр усложняет задачу, но для «cумм» и иногда для «неравенств» их нет вообще.
Игровое поведение начинающего любителя судоку можно сравнить с методикой начинающего шахматиста, быстро тонущего в океане расчётов по принципу «он — туда, я — сюда…». Умение отбрасывать лишние, ненужные варианты в расчётах — проводить перебор с ограничениями — одно из главных преимуществ «обученного» игрока и в шахматах, и в судоку.
Перебирать варианты всё равно придётся, без этого не обойтись, но с помощью ряда приёмов можно сократить объём работы во много раз. Разберём несколько таких приёмов на примерах.
Метод крайнего элемента. Это словосочетание известно каждому, кто посещал занятия в математическом кружке. В нашем случае слово «крайний» будет означать «экстремальный» (т. е. наименьший или наибольший).
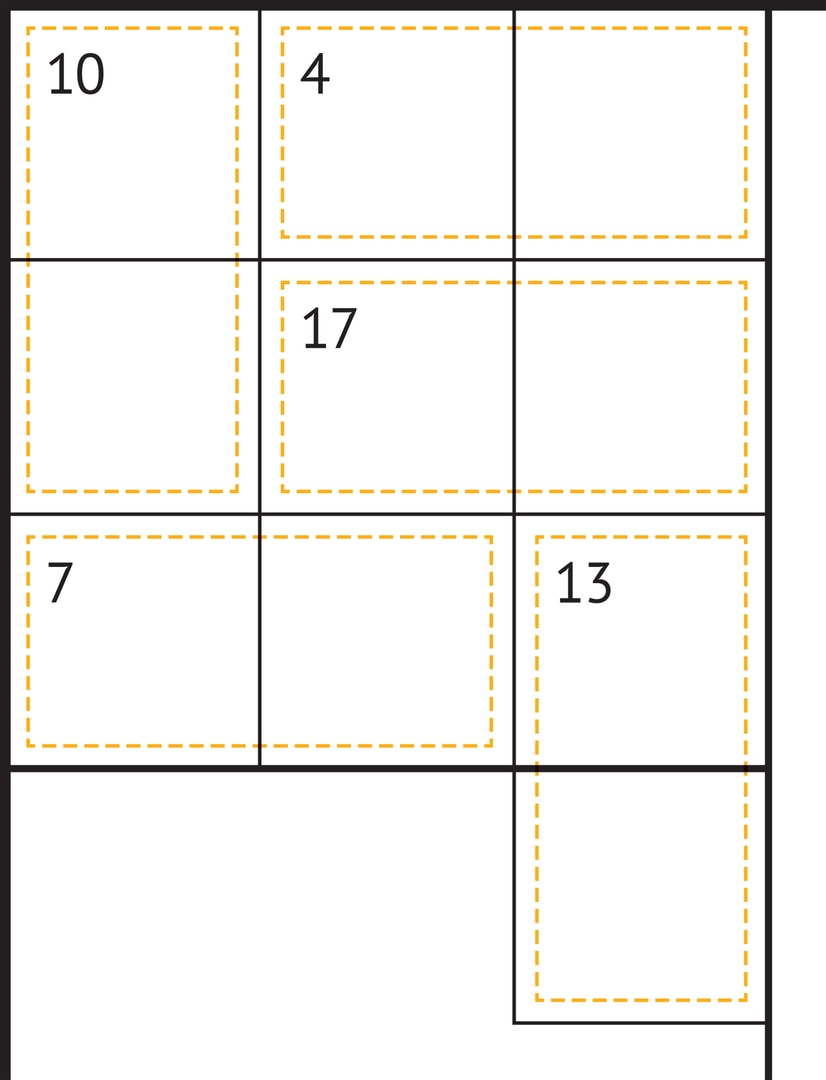
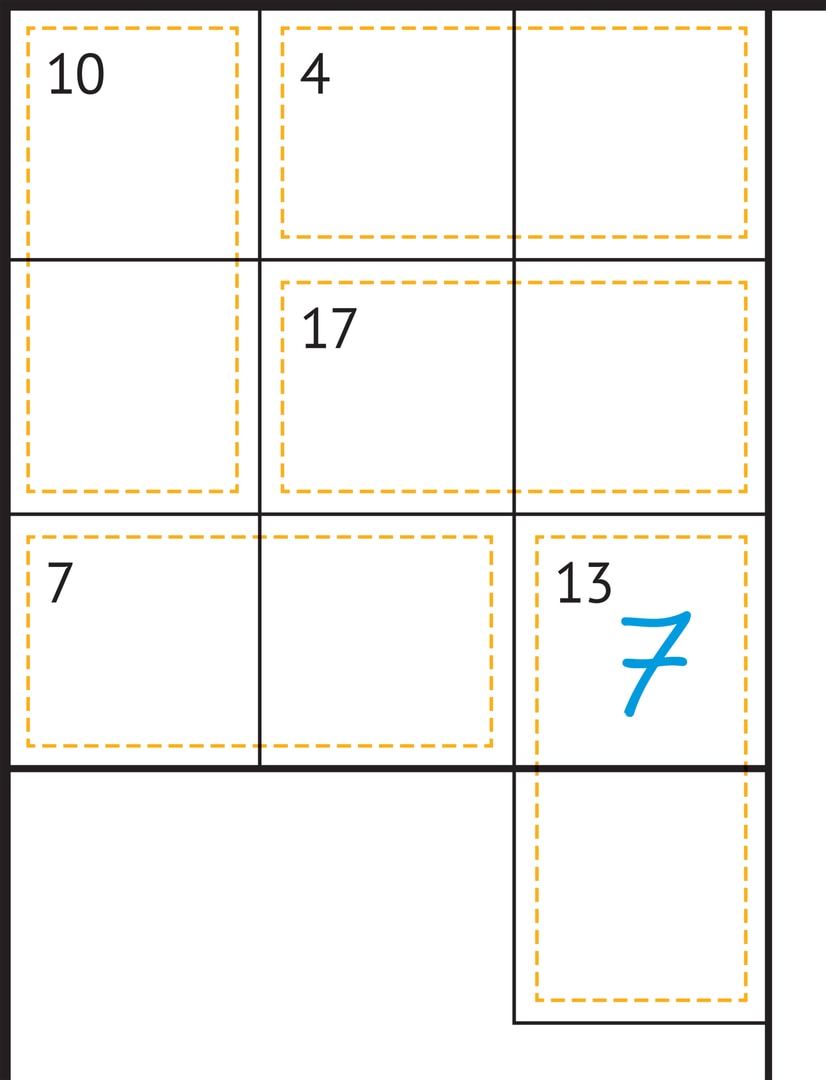
Например, при разгадывании судоку «суммы» ограничения в переборе можно получить, отметив в таблице все блоки из двух клеток, суммы в которых равны 3, 4, 16, 17. Это и есть «крайние» элементы, наименьшие и наибольшие. Каждое из этих чисел единственным образом представляется в виде суммы двух разных цифр (отличных от нуля): $$ 3=1+2,\quad 4=1+3,\quad 16=7+9,\quad 17=8+9. $$
А для других чисел вариантов было бы больше, например, $7=1+6=2+5=3+4$.
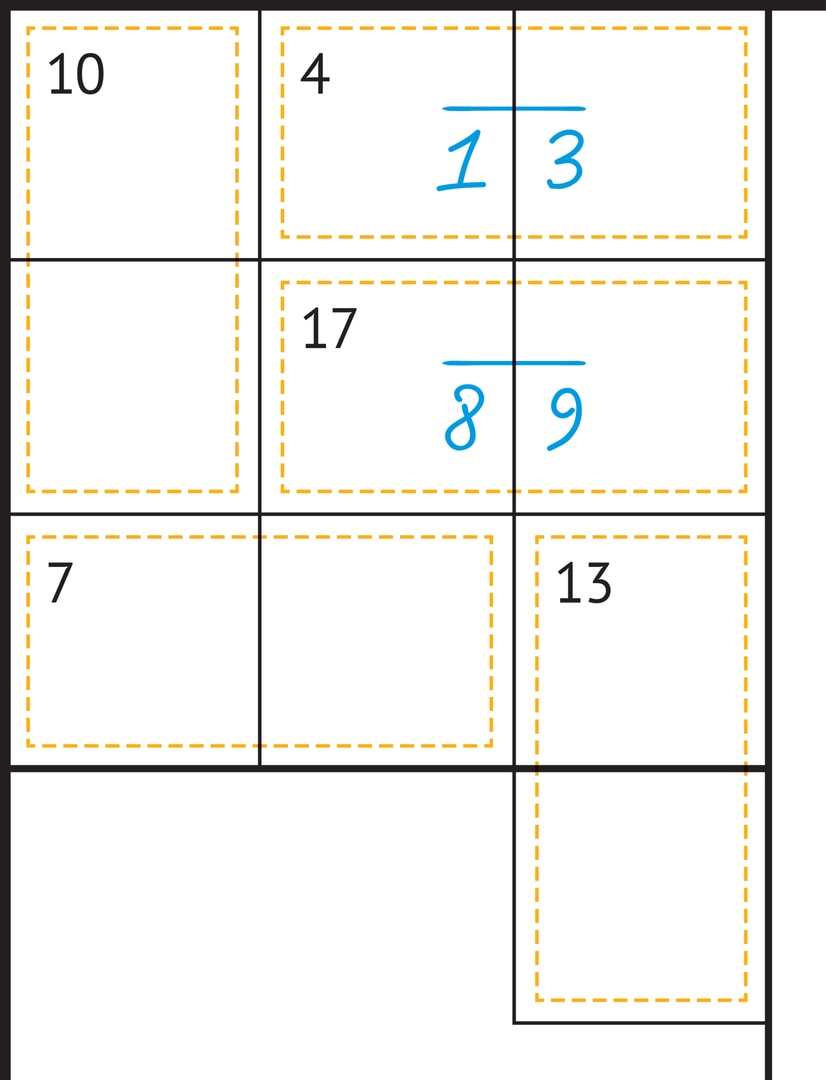
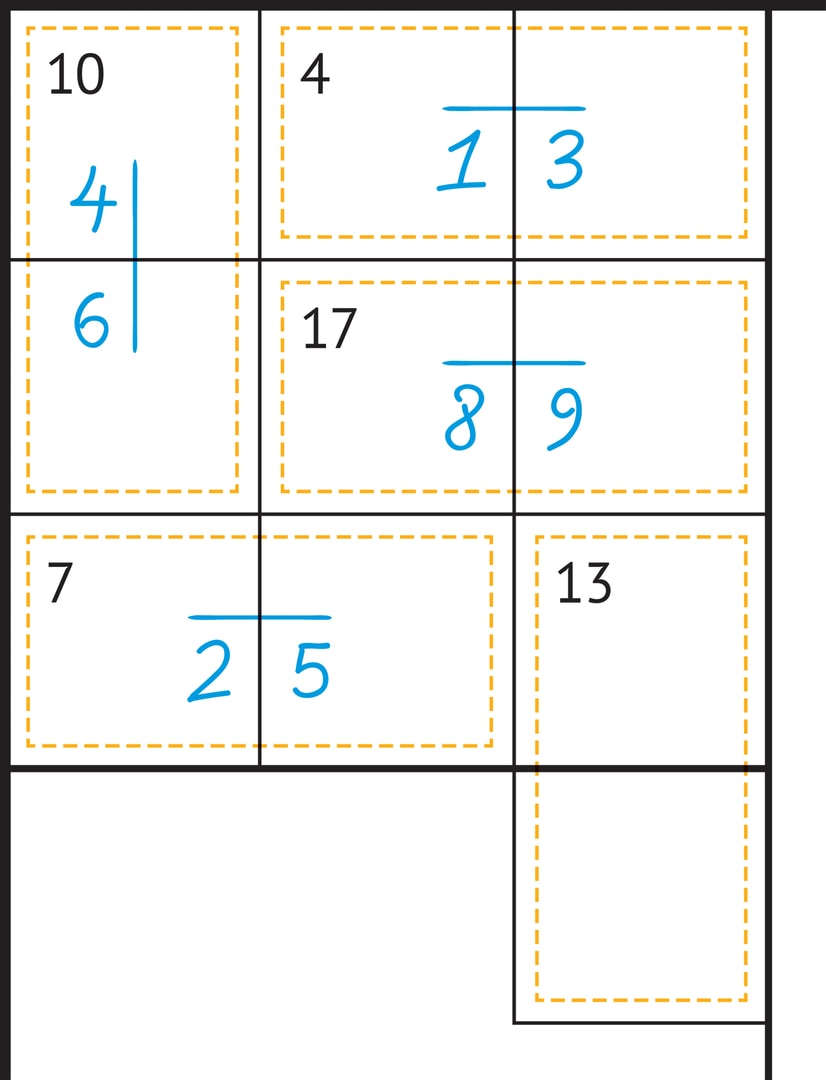
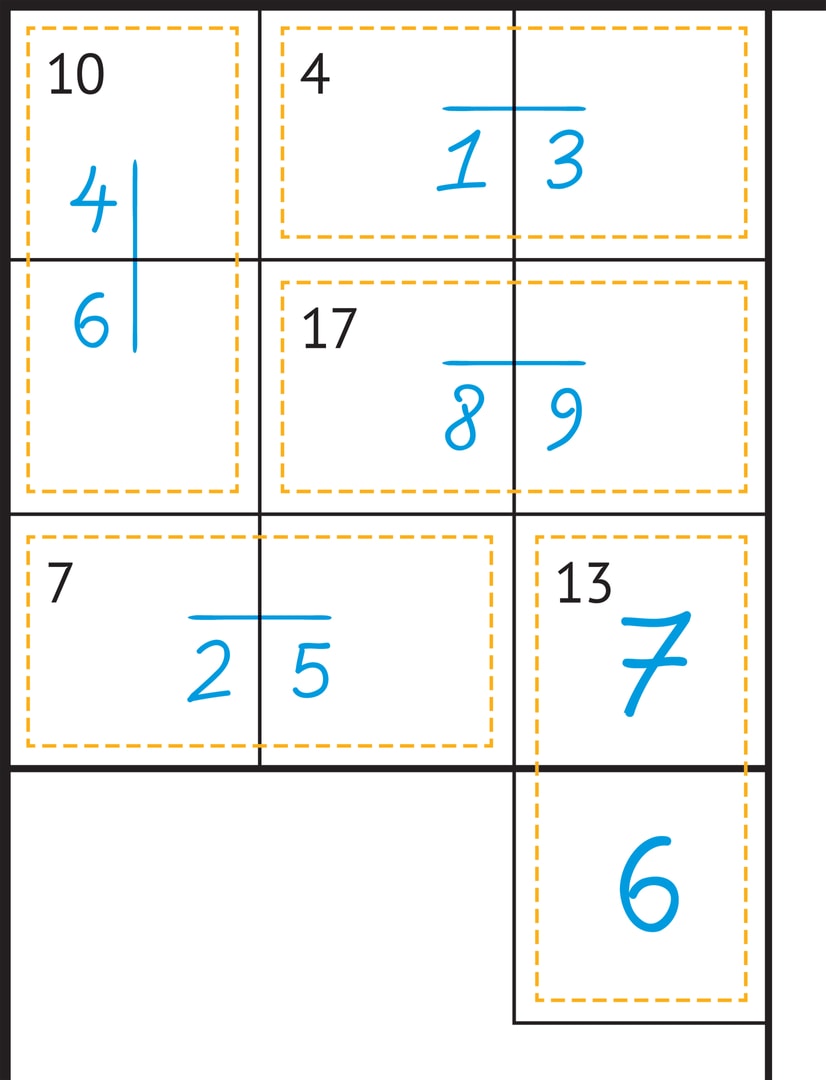
На рисунке, иллюстрирующем подобный пример, две такие «крайние» области, в соответствующих клетках будут находиться (в неизвестном нам пока порядке) цифры 1, 3 и 8, 9. Это сразу даёт «ограничение» для выделенного квадрата — числа 7 и 10 из неиспользованных цифр можно сложить единственным образом: $7=2+5$, $10=4+6$. Теперь в этом квадрате $3 \times 3$ осталась неиспользованной только цифра 7, которая и отправляется в правый нижний угол. После этого определяется и сосед цифры 7 по выделенной области — цифра 6.
Переход к дополнению. Идея состоит в том, что для изучения части данного множества может быть полезным изучение дополняющей части. Вот поясняющий пример, навеянный знаменитой историей про Архимеда. Даны мерный стаканчик и шарик, объём которого надо быстро определить. Кладём шарик в стакан, заливаем водой с верхом, запоминаем отметку на шкале, вынимаем шарик, смотрим на новую отметку. Разность объёмов, определяемых первой и второй метками, равна объёму шарика.
Вернёмся к разобранному ранее примеру. Цифру 7 в правом нижнем углу квадрата $3\times 3$ можно «поставить на место» и с помощью приёма «переход к дополнению».
Правая нижняя клетка квадрата является частью «языка», уходящего в соседний квадрат, а все остальные области с обозначенными суммами за пределы квадрата $3\times 3$ не выходят. Cумма цифр по всем клеткам любого квадрата разбиения $3\times 3$ равна $$1+2+…+9=45,$$ а сумма цифр во «внутренних» областях с суммами данного квадрата равна $10+4+17+7=38$. Эти цифры «дополняют» цифру в правом нижнем углу квадрата, она равна $45-38=7$.
Блочный метод. В нашем случае блоки — это одинаковые наборы цифр.
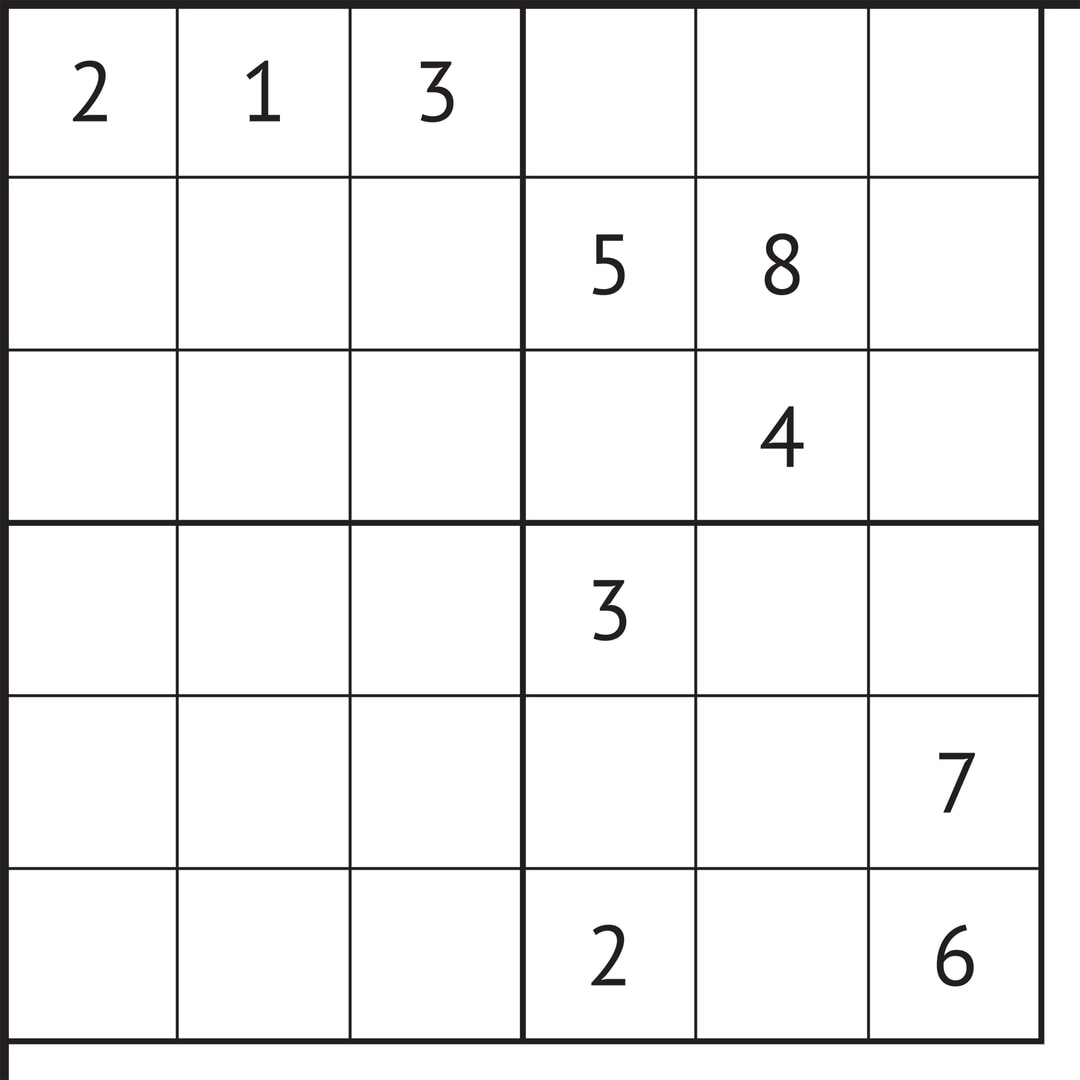
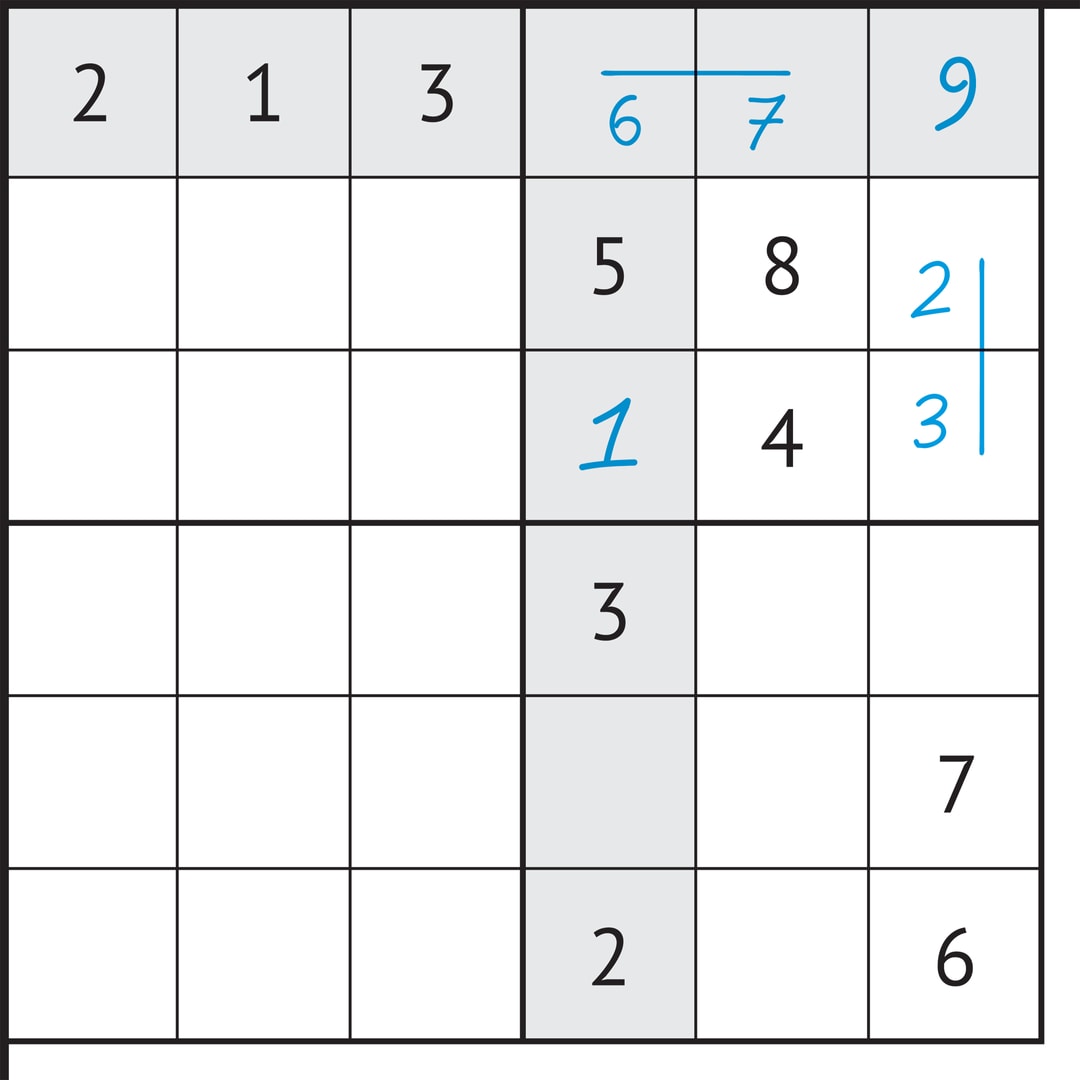
В следующем примере из классического варианта судоку блок (2, 3) встречается в первой строке и в четвёртом столбце. В правом верхнем квадрате $3\times 3$ упомянутые строка и столбец «закрывают» для цифр блока $(2, 3)$ все клетки, кроме двух. Затем, в этом квадрате последовательно определяем место 1, место блока $(6, 7)$, место 9.
Можно считать, что место для 9 было найдено методом перехода к дополнению — другими цифрами были заняты восемь из девяти мест в квадрате $3\times 3$.
Связность. В математике линейная связность множества — свойство, означающее, что любые две его точки можно связать непрерывной кривой, не выходящей за границы множества.
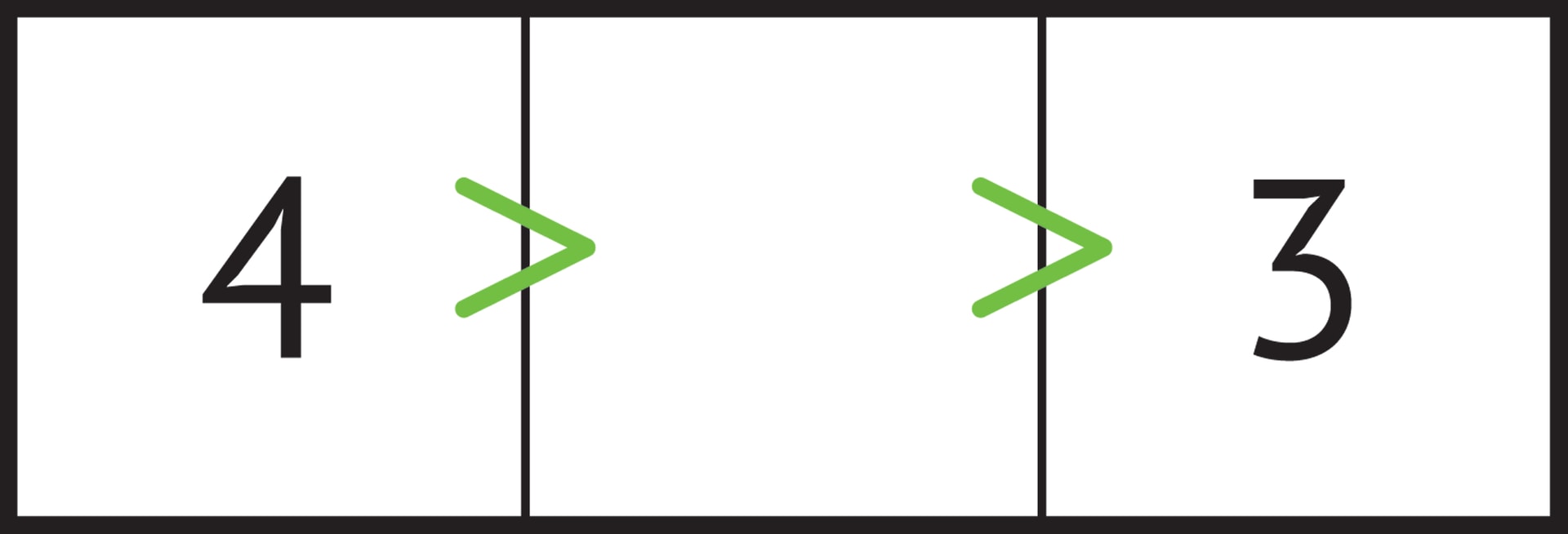
В судоку «неравенства» такой линией можно считать цепочку неравенств, связывающую группу подряд идущих цифр. Идею метода иллюстрирует приведённый пример. Такая ситуация в расчётах должна быть исключена, так как между 3 и 4 цифр нет, связность нарушается.
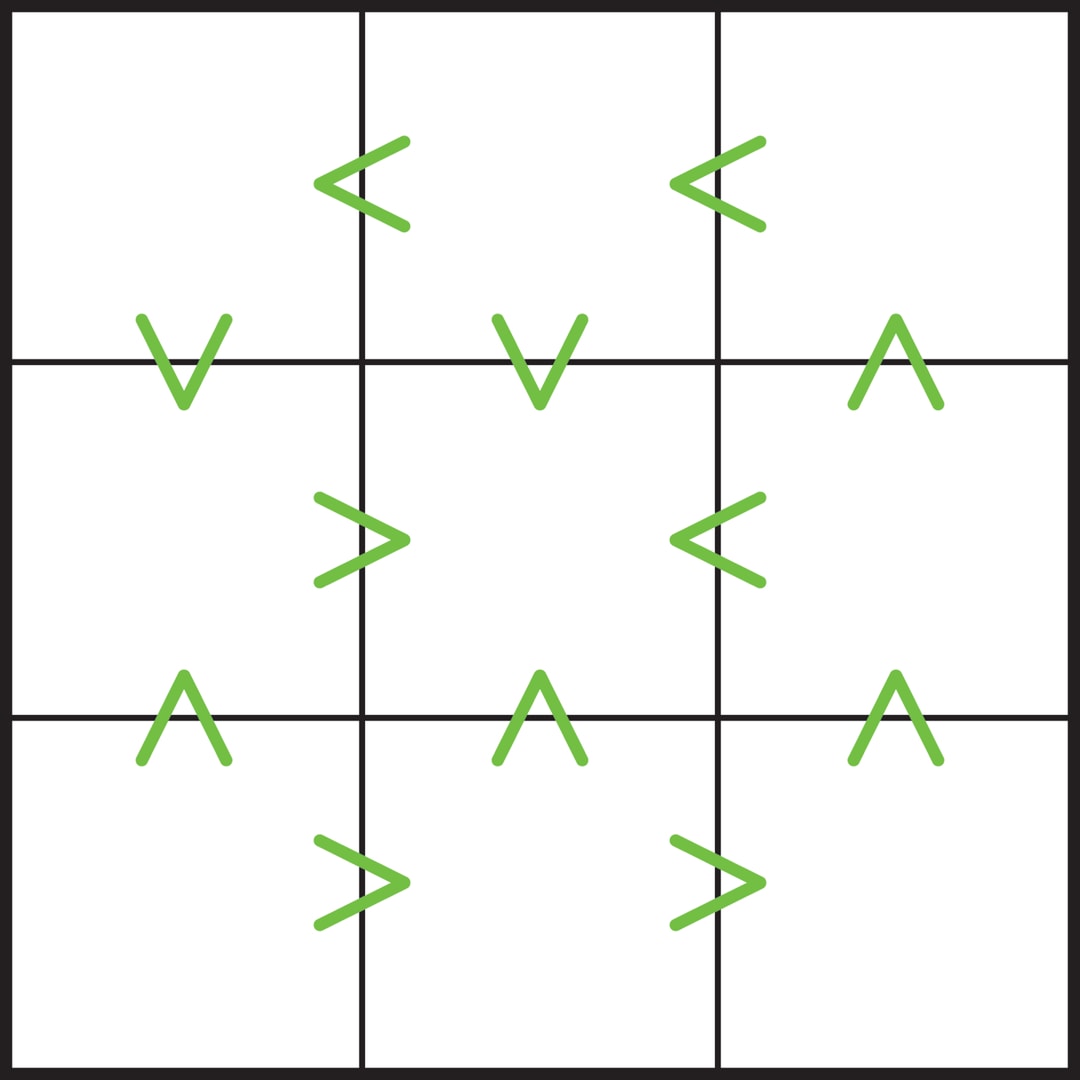
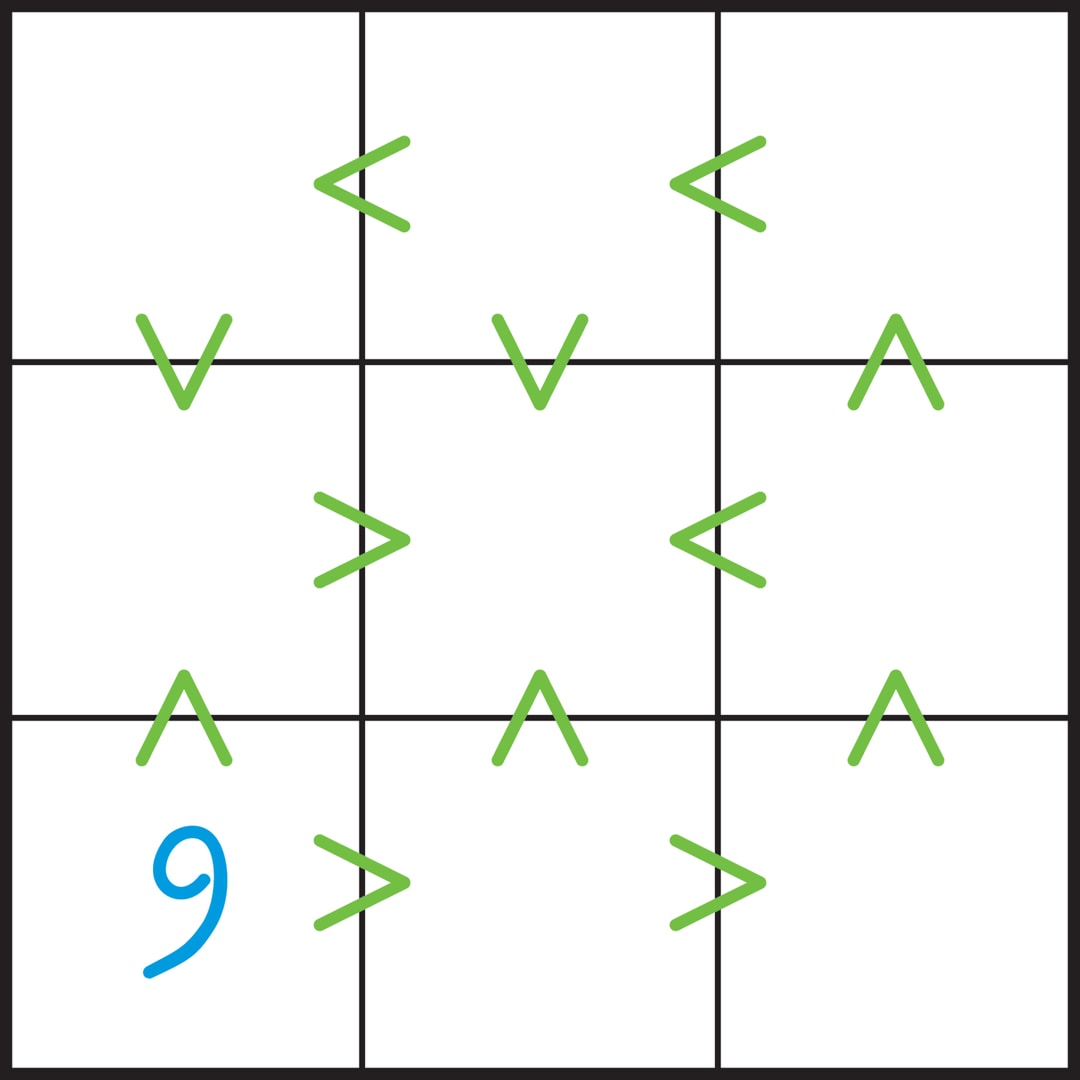
В судоку «неравенства» важен и метод крайнего элемента, в частности 1 и 9 играют особую роль. Комбинируя эти методы, можно решать задачи, в которых в начальной позиции нет ни одной цифры!
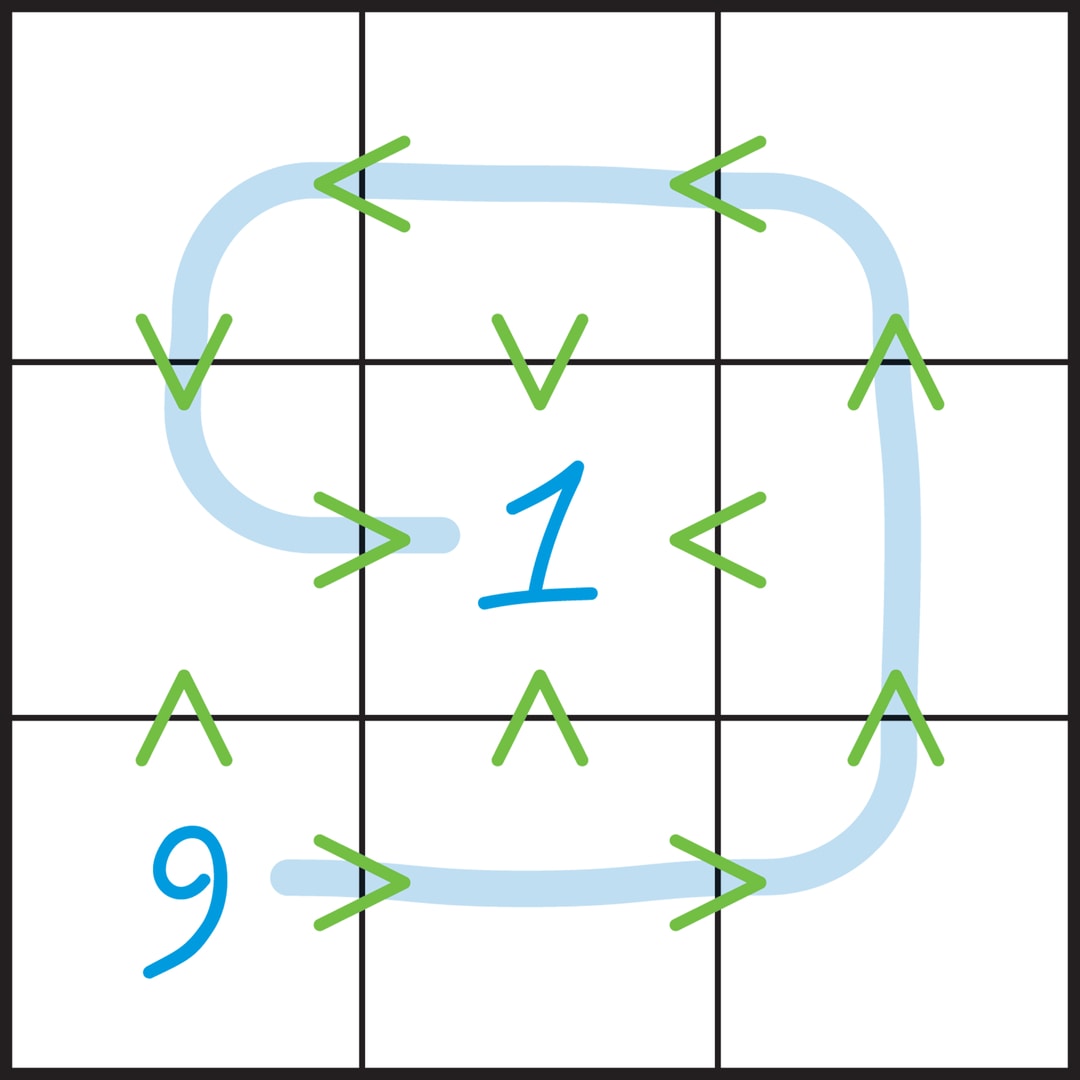
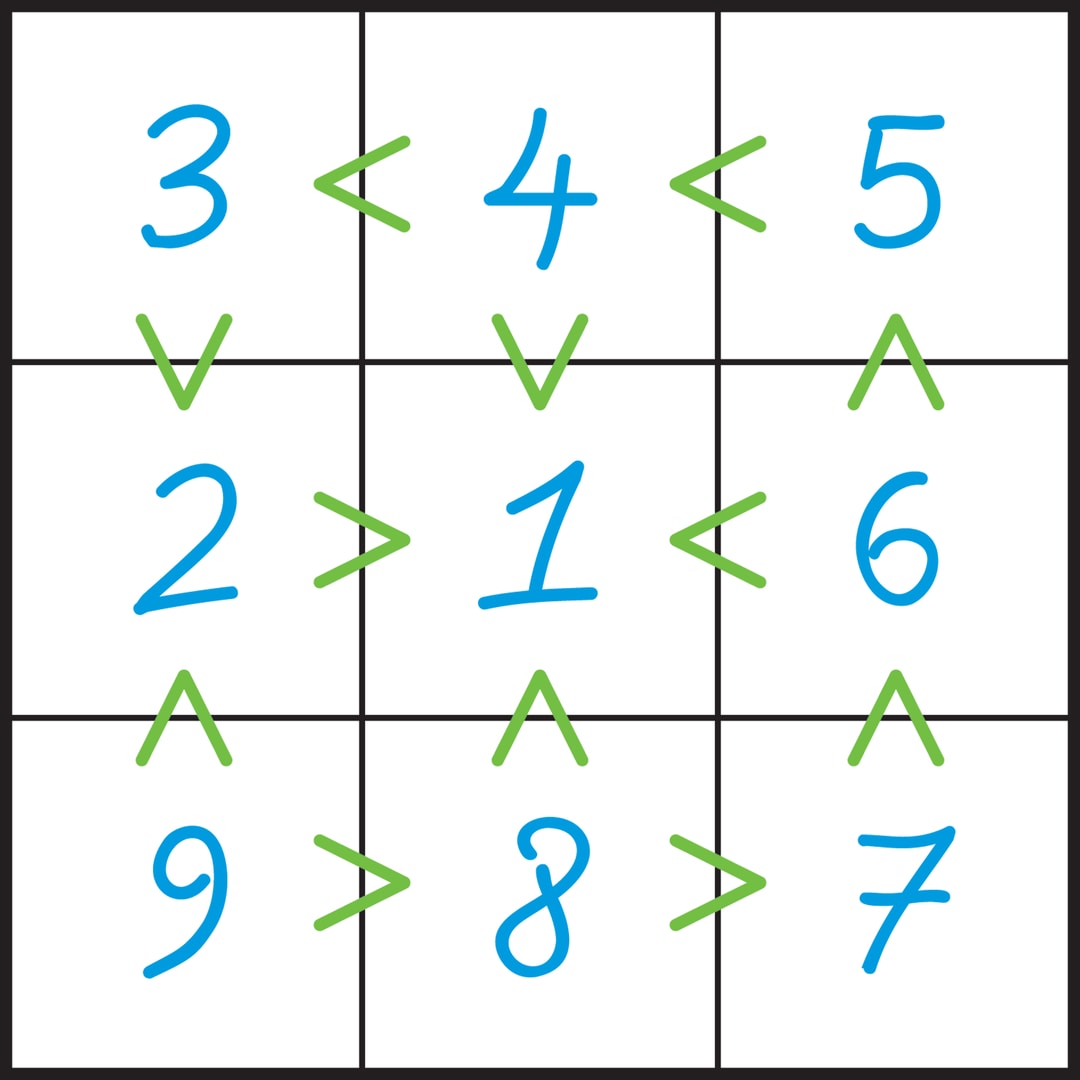
Сначала определим крайние элементы. Единственная клетка, из которой выходят только знаки «больше», — левая нижняя клетка, значит, в ней находится цифра 9. Это своеобразный источник, вершина горы. Аналогично, средняя клетка — единственная, обитатель которой меньше соседей, — в ней находится 1. Теперь становится очевидным то, что клетки с 9 и с 1 связывает «ручей», который заполняют цифры 8, 7, …, 2.
Конечно, в реальных задачах вида «неравенства» (как, впрочем, и во всех других видах) учитываются и соображения, связанные с неповторяемостью цифр в строках и столбцах таблицы $9\times 9$.
Приведённые примеры превращений математических терминов в игровые приёмы судоку подтверждают справедливость латинского изречения nomen est omen: имя — уже значение.