Крышки люков, спасающие пешеходов от падений в колодцы и мешающие автомобилистам, чаще всего имеют круглую форму. Выбор такой формы объясняется соображениями безопасности — квадратная крышка при сдвиге может провалиться, поскольку сторона квадрата меньше его диагонали. А у круга есть замечательное свойство — это фигура постоянной ширины.
Постоянная ширина означает, что при «обхвате» фигуры двумя параллельными прямыми ширина полученной полосы будет постоянной, не зависящей от выбора направления прямых.
А есть ли на плоскости, помимо круга, другие фигуры постоянной ширины? Оказывается, есть, и их бесконечно много.
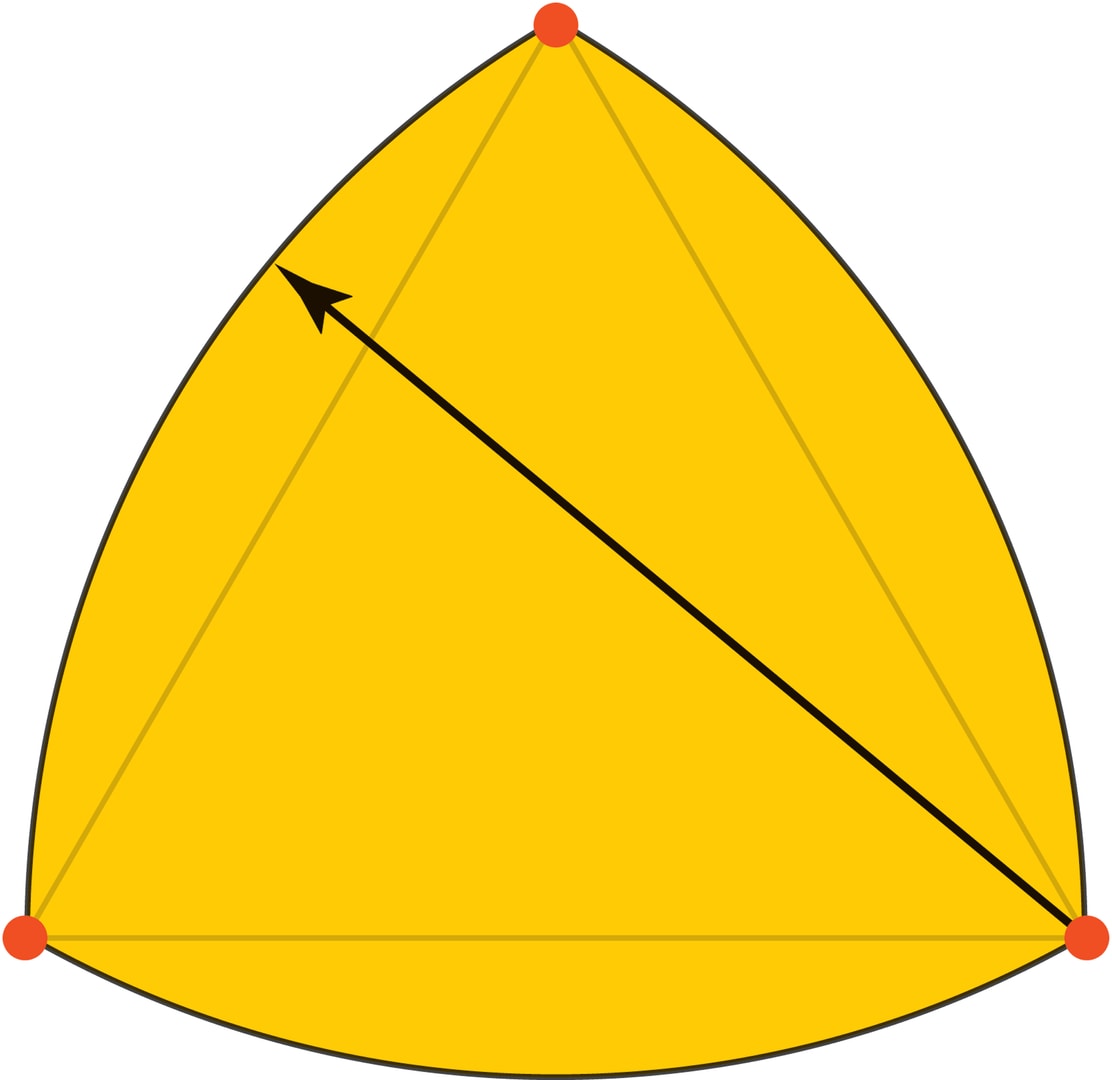
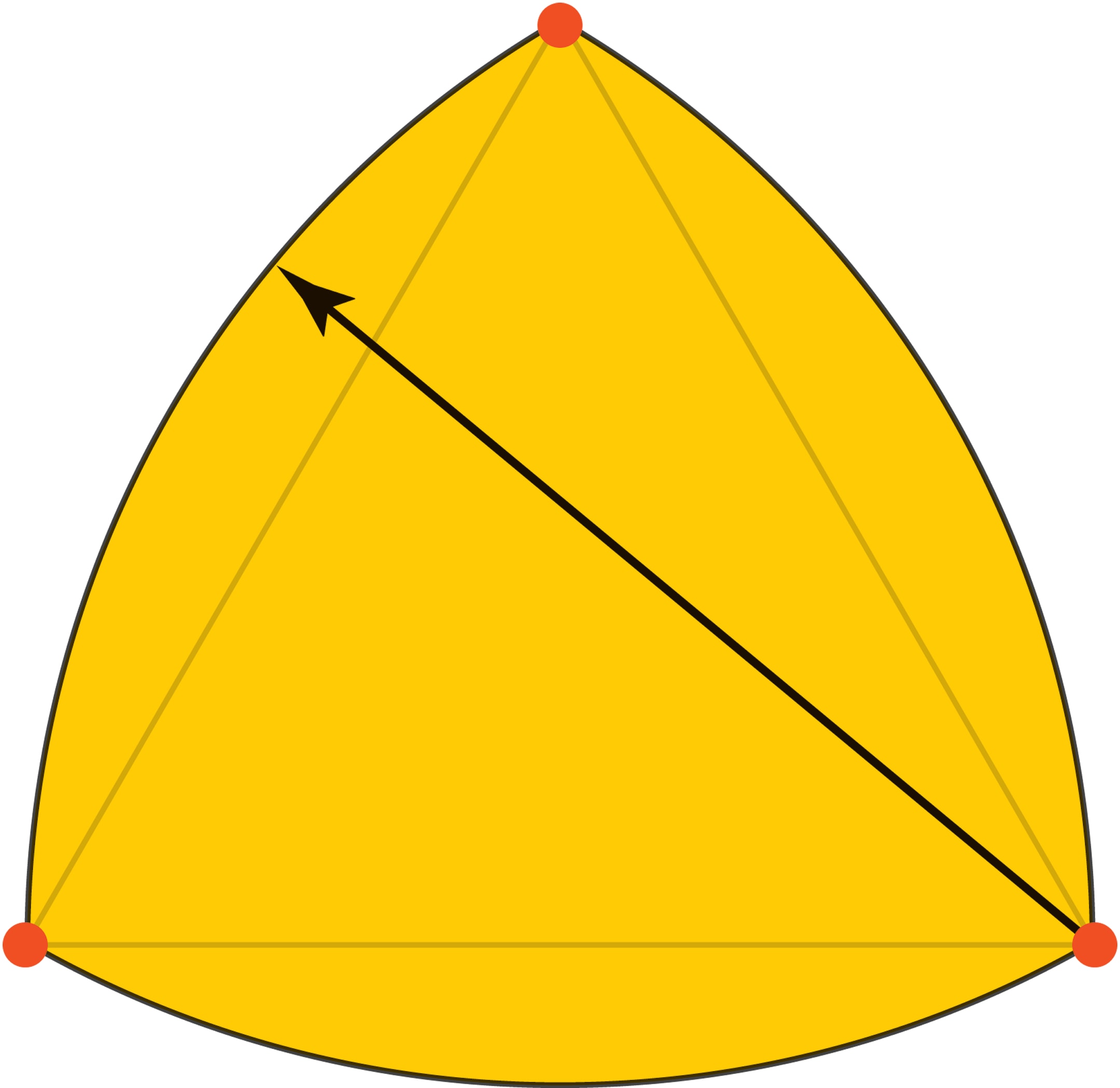
Самая простая и самая знаменитая такая фигура — треугольник Рёло. Точнее говоря, эта фигура только напоминает треугольник, её граница — дуги трёх окружностей с центрами в вершинах правильного треугольника и одинаковых радиусов, равных длине стороны треугольника. Можно показать (и «проверить» с помощью штангенциркуля), что при обхвате фигуры параллельными прямыми точками касания прямых для треугольника Рёло будут одна из его вершин и какая‐то точка на противолежащей этой вершине дуге окружности. Так как радиусы всех дуг равны, то результат «измерения» всегда будет одинаков.
По той же схеме, что и для треугольника, фигуру постоянной ширины можно построить на любом правильном $n$‐угольнике, имеющем нечётное число вершин. Можно построить и несимметричные фигуры постоянной ширины.
Житейски, свойство постоянной ширины фигуры можно продемонстрировать, изготовив набор роликов с профилями различных фигур фиксированной постоянной ширины. Если положить ролики на горизонтальную поверхность и накрыть дощечкой, то при качении роликов дощечка будет перемещаться горизонтально.
У фигур постоянной ширины немало интересных свойств. Например, все фигуры данной постоянной ширины имеют одинаковый периметр. Есть у таких фигур и своеобразная иерархия. А именно, среди фигур данной постоянной ширины наибольшая площадь — у круга, наименьшая — у треугольника Рёло.
Благодаря своим геометрическим свойствам, фигуры постоянной ширины находят применение в различных областях.
Первый пример. Вы опускаете монету в автомат и она отправляется в путь по монетоприёмнику. Чтобы монета не застряла, можно, конечно, расширить трубку. А можно изготавливать монеты в виде фигур постоянной ширины, тогда монета не застрянет, даже вращаясь.
Простейшая фигура постоянной ширины, как мы знаем, — круг, форму которого имеет большинство монет. Но есть и исключения. В Великобритании 20‐ и 50‐пенсовые монеты имеют форму фигуры постоянной ширины, построенной на правильном семиугольнике. Такую же форму имеет и монета достоинством в полдинара, имеющая хождение в Иордании. Изготовление монет в виде фигур постоянной ширины, отличных от круга, позволяет экономить металл: ведь как мы знаем, при фиксированной ширине круглая монета — самая металлоёмкая.
В двух других примерах треугольник Рёло скрыт от глаз, но является главной идейной составляющей конструкции.
До наступления цифровой эпохи фильмы снимали на плёнку. И в кинокамерах, и в кинопроекторах были грейферные механизмы, обеспечивавшие скачкообразное движение плёнки вдоль объектива (стандартно 18 скачков в секунду). Движение этих механизмов задавал треугольник Рёло.
В автомобилестроении в конце 1940‐х годов Ф. Г. Ванкель придумал схему двигателя без коленчатого вала — устройства, преобразующего поступательное движение поршней во вращение вала мотора. В этом двигателе, называемом роторным, нет цилиндров. Тело, называемое ротором, при вращении постоянно касается стенок камеры двигателя, разделяя рабочее пространство на три части. В двигателе Ванкеля форма ротора в сечении — треугольник Рёло.
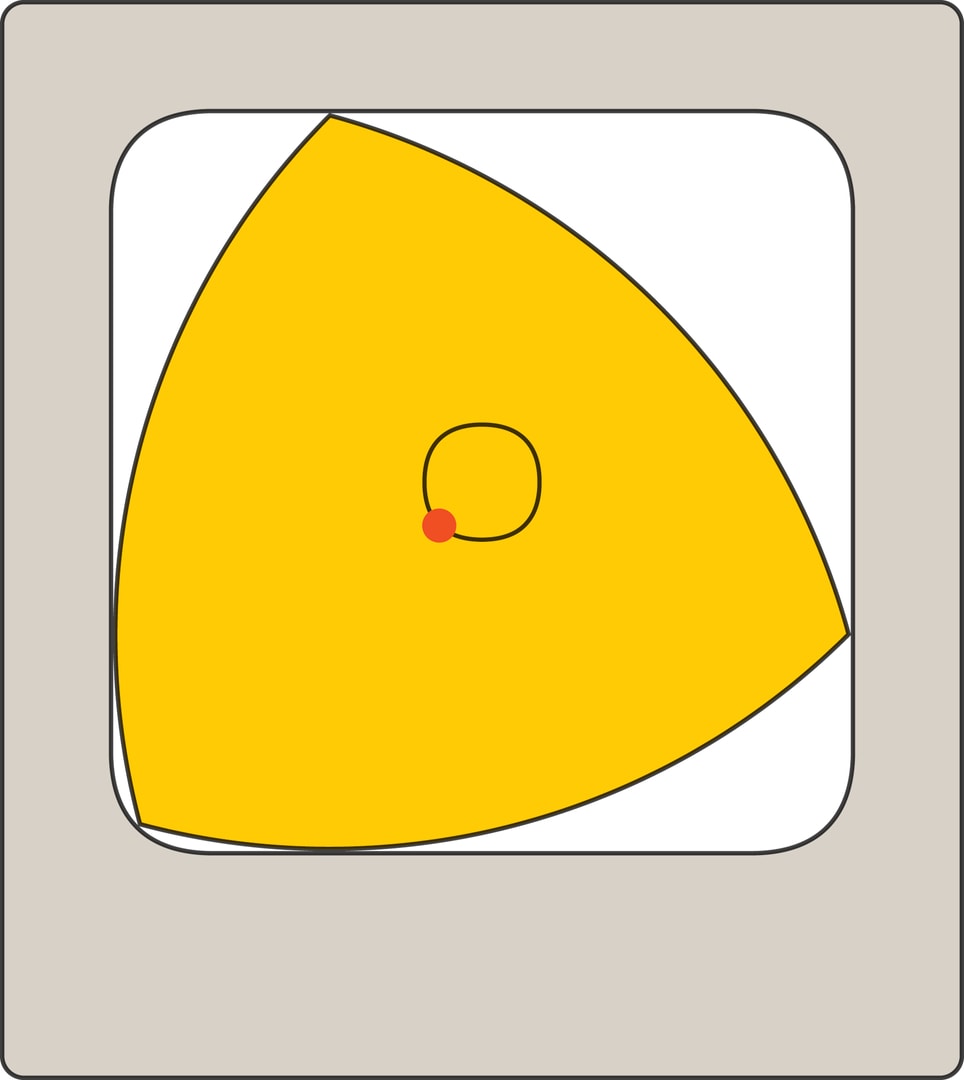
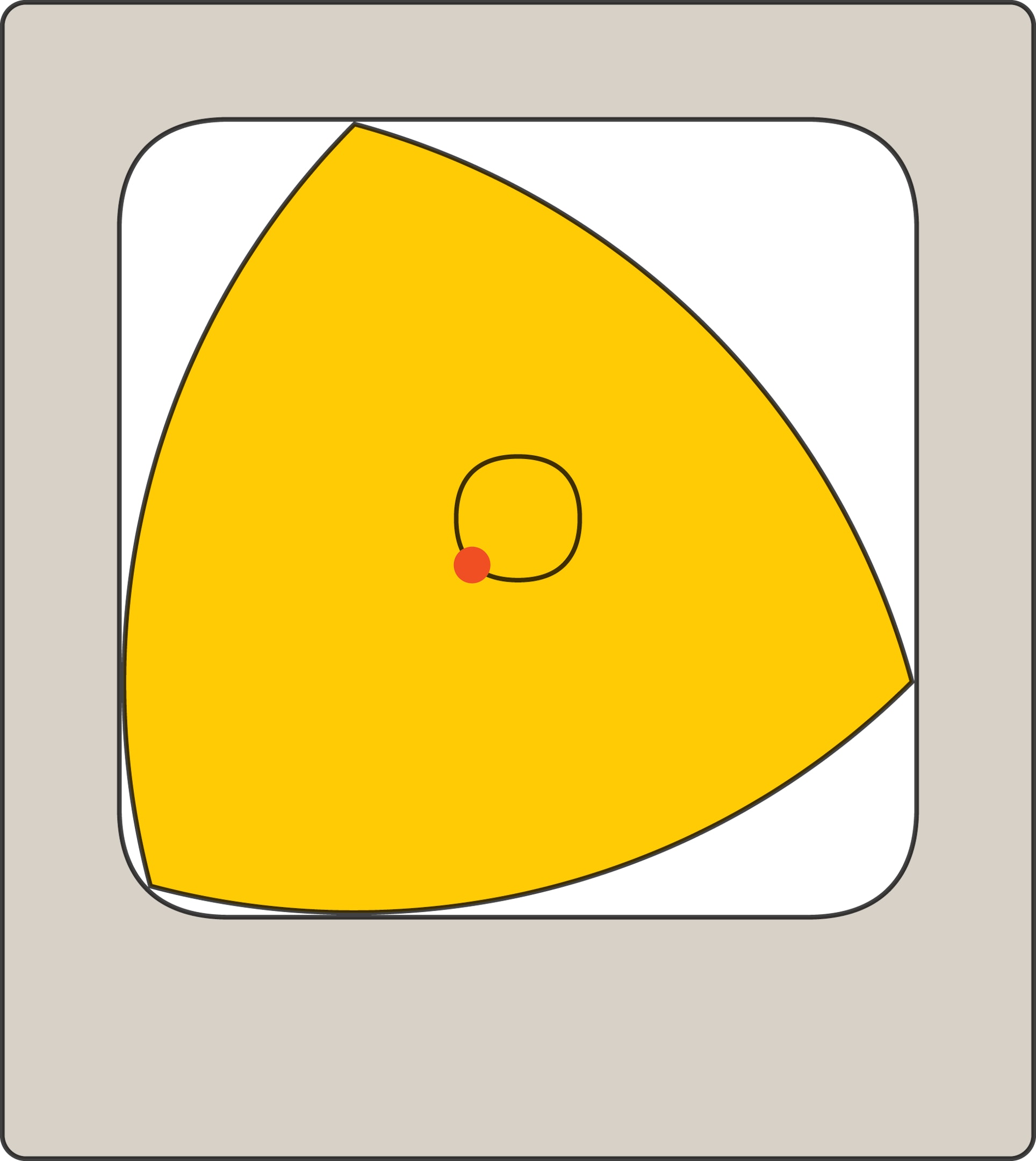
Возвращаясь к геометрии заметим, что если центр треугольника Рёло двигается по специальной замкнутой кривой, а сам треугольник при этом вращается вокруг центра, то заметаемая область имеет форму квадрата, углы которого немного закруглены. С использованием этой идеи разработано и запатентовано сверло, позволяющее получать почти квадратные отверстия!
На плоскости у фигур постоянной ширины $d$ одинаковый периметр, равный $π d$, как у окружности диаметра $d$ (теорема Барбье). А площадь может быть разной: наименьшая — у треугольника Рёло, наибольшая — у круга.
В трёхмерном пространстве можно выделить класс тел постоянной ширины, только обхват фигуры производится не параллельными прямыми (как в двумерном случае), а параллельными плоскостями. Примеры: шар и тело, получающееся при вращении треугольника Рёло вокруг оси симметрии. У этих фигур при одинаковой ширине площадь поверхности разная, т. е. у теоремы Барбье аналога нет. Остались и нерешённые задачи, например: среди тел постоянной ширины $d$ найти тела с наименьшей поверхностью и наименьшего объёма.
Было отмечено, что круг имеет наибольшую площадь среди фигур заданной постоянной ширины. Но исторически раньше появились и были изучены изопериметрические задачи, в которых надо найти фигуру наибольшей площади при заданном периметре и при заданных ограничениях на форму границы (популярное изложение см. в книгах: Тихомиров В. М. «Рассказы о максимумах и минимумах» и Протасов В. Ю. «Максимумы и минимумы в геометрии»). Если ограничений нет, то это круг. А если частью границы является отрезок, длина которого не учитывается как часть периметра, то это полукруг (задача Дидоны). Из изучения подобных задач родилась целая математическая дисциплина — вариационное исчисление.
Задача Дидоны названа так в честь легендарной финикийской царевны, основательницы Карфагена. Бежавшая из города Тир царевна остановилась на берегу современного Туниса и на встрече с местными вождями попросила их продать немного земли. Те «дружелюбно» ответили, что Дидона может взять столько земли, сколько можно покрыть шкурой быка, на которой они сидят. Однако Дидона разрезала шкуру на тонкие ремни, связала их и огородила большой участок на берегу моря. Основанная крепость Карфагена носила название Бирса, что означало «шкура». В «Энеиде» римского поэта Вергилия приплывший в Карфаген Эней слышит такой рассказ:
В эти приплыли места, где теперь ты могучие видишь
Стены, где ныне встаёт Карфагена новая крепость.
Здесь купили клочок земли, сколько можно одною
Шкурой быка охватить (потому и название Бирса).
Яглом И. М., Болтянский В. Г. Выпуклые фигуры. — М.—Л.: ГИТТЛ, 1951. — (Библиотека математического кружка; Вып. 4).
Радемахер Г., Тёплиц О. Числа и фигуры: Опыты математического мышления. — М.: ОНТИ, 1936. — (Библиотека математического кружка; Вып. 10). — [Переиздания: 1938, 1962, 1966, 2020]. — [§ 25 «Кривые постоянной ширины»].
Кривые (фигуры) постоянной ширины