Ориентация, ориентироваться — эти слова связаны с определением положения объекта относительно сторон света (латинское oriens — восток), более широко — в некоторой системе координат. Задача управления ориентацией возникает и для реальных объектов (космические аппараты, самолёты, корабли, беспилотные устройства), и для виртуальных (например, в компьютерных играх). Во всех случаях изменение ориентации — результат движения тела в пространстве.
Рассмотрим задачу с математической точки зрения. Сначала разберёмся в структуре движения, узнаем, из каких элементов оно состоит.
Великий Леонард Эйлер доказал, что если движение (твёрдого) тела имеет неподвижную точку, то это поворот тела вокруг некоторой оси. Неподвижными оказываются все точки данного объекта, лежащие на этой оси!
Если тело вращается вокруг оси, которая не имеет с ним общих точек, то неподвижных точек нет (тело «летает» вокруг оси по кругу подобно кордовой модели самолёта). Ещё один пример движения без неподвижных точек — параллельный перенос. В начале XIX века было установлено, что любое движение тела — композиция (последовательное выполнение) переноса и поворота, ось которого параллельна направлению переноса.
Говоря об ориентации твёрдого тела, можно считать, что есть неподвижная точка (например, центр масс). В этом случае по теореме Эйлера набор движений сводится к поворотам, каждый задаётся осью и углом. Технически описать повороты можно разными способами. Самые популярные инструменты — углы Эйлера и кватернионы.
Углы Эйлера представляют поворот тела как результат трёх последовательных вращений вокруг координатных осей, связанных с телом. В приложениях и в теоретической механике разработаны различные реализации этой идеи.
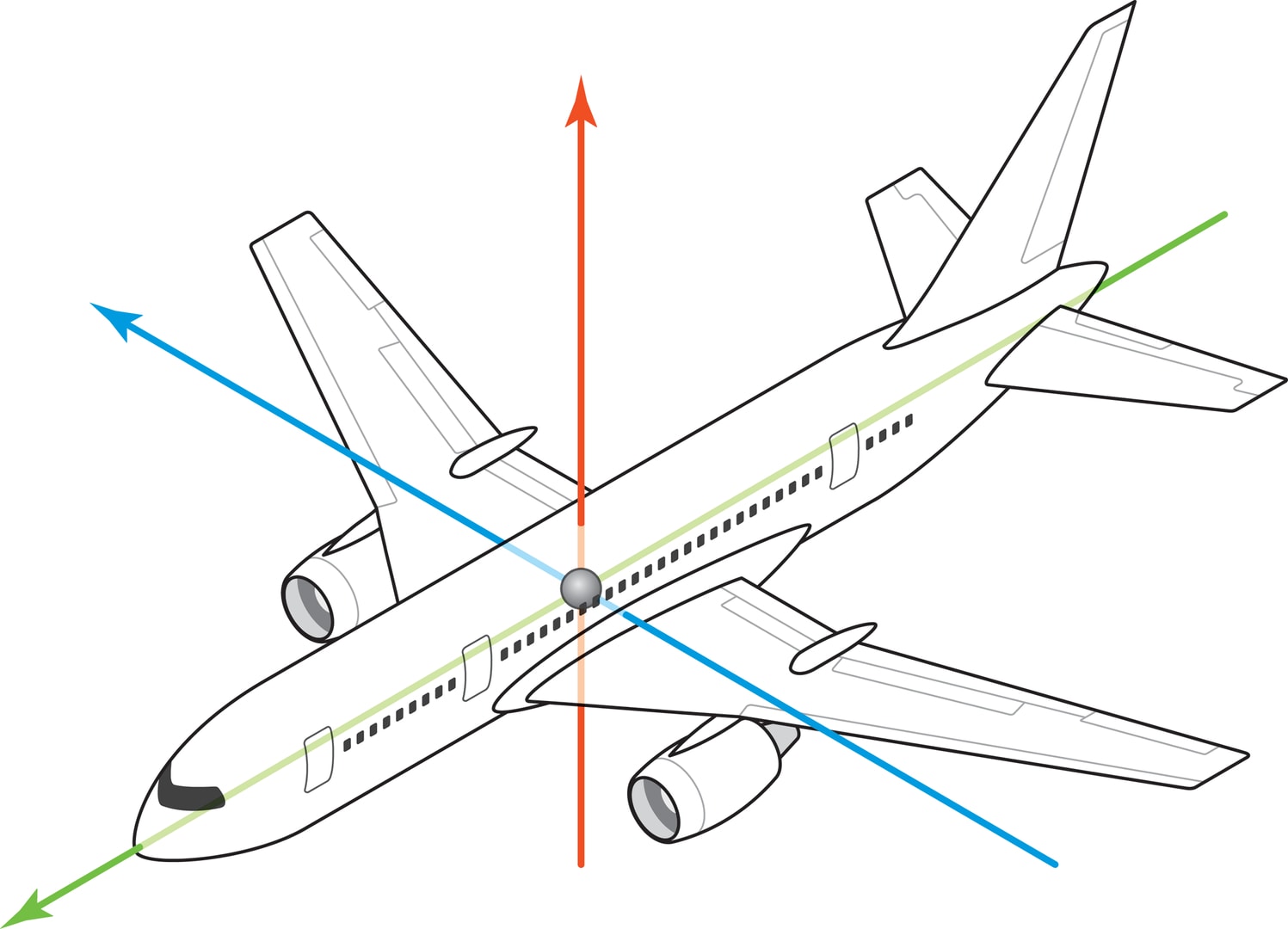
Например, в авиации и в морском деле традиционно используется система координат, оси которой естественно связаны с корпусом самолёта (корабля): $Ox$ — ось движения, $Oy$ — перпендикулярная плоскости крыльев (палубы) ось,} $Oz$ — ось, перпендикулярная плоскости $Oxy$.
Поворот (ориентация) самолёта или корабля определяется тремя последовательными вращениями вокруг оси $Ox$, вокруг оси $Oy$, вокруг оси $Oz$ (углы поворотов относительно этих осей называются крен, рыскание, тангаж). Порядок поворотов важен, поскольку перестановка двух вращений может изменить результат. Данную модификацию углов Эйлера обычно связывают с именем математика и кораблестроителя А. Н. Крылова.
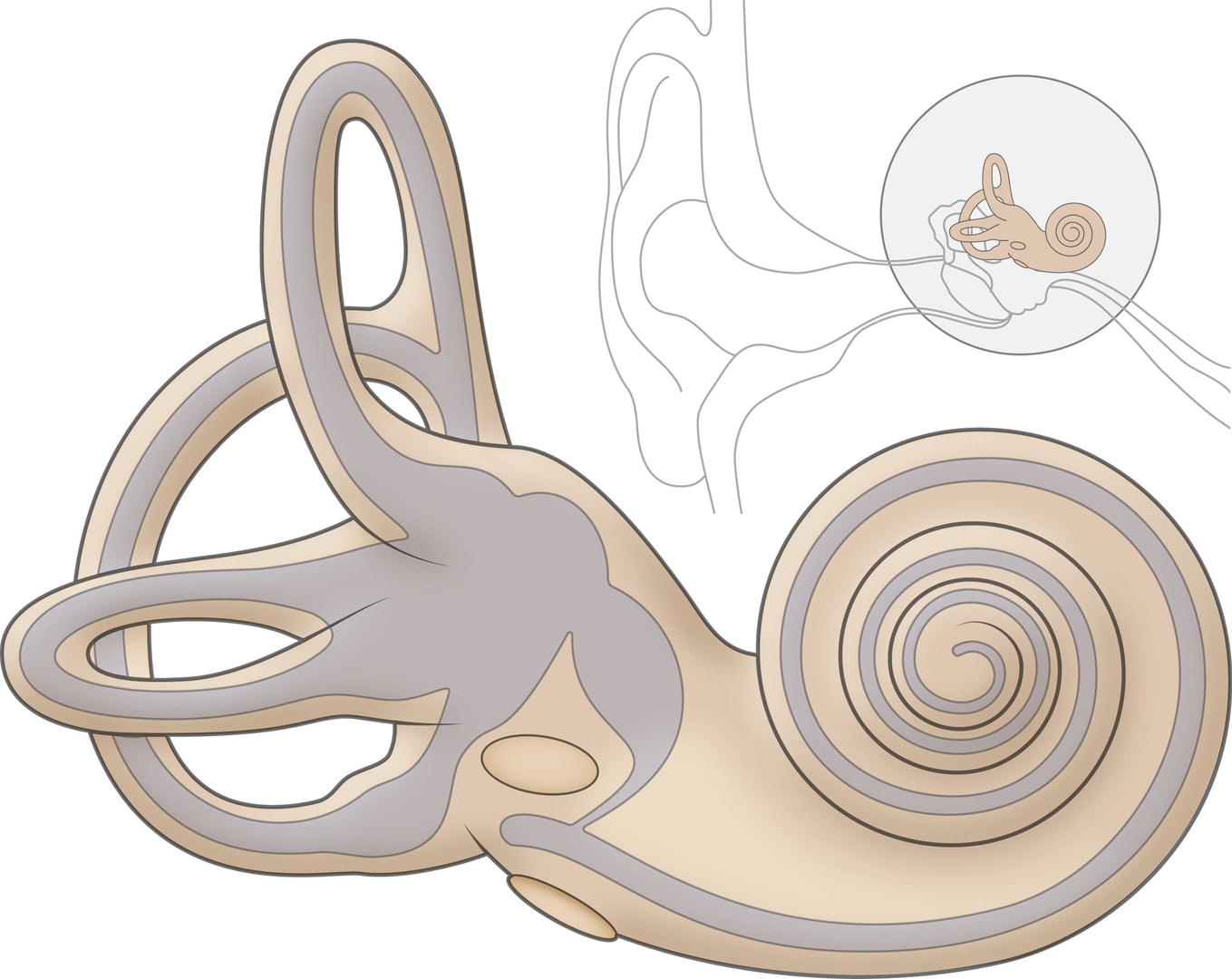
Применение углов Эйлера популярно в силу наглядности и удобства управления этими параметрами. Да и в природе такое решение уже существует. За ориентацию в пространстве у человека отвечает вестибулярный аппарат, «антенны» которого называются полукружными каналами — три кругообразные дуги в каждом ухе, расположенные во взаимно перпендикулярных плоскостях.
То, что углов Эйлера мало, всего три, конечно, удобно. Но это обстоятельство является и недостатком: можно доказать, что для математически «правильного» представления поворотов в трёхмерном пространстве трёх параметров не хватает. Следствием этих математических нестыковок являются проблемы практические, возникающие при использовании углов Эйлера.
Серьёзные трудности могут возникнуть в стандартной задаче управления ориентацией. В неподвижной системе координат (которую «хранит», например, бортовой гироскоп) задаются начальное и конечное положение объекта, а изменению ориентации надо сопоставить углы Эйлера. Такое соответствие должно быть однозначным и устойчивым. А как раз эти свойства могут оказаться под угрозой при некоторых заданных начальном и конечном положениях. Одна из подобных проблем носит название «складывание рамок» (происходит от термина из теории гироскопов). Поясняющий пример: вы следите за приближающейся стаей птиц, и когда она оказывается прямо над вашей головой, придётся резко повернуться, потому что запрокинуть голову дальше не удастся.
Процессы изменения ориентации, задаваемые углами Эйлера, обладают и другими неприятными свойствами, пусть и не катастрофическими. Разделённо-последовательное вращение вокруг трёх осей приводит к движениям, далёким от оптимальных, экономичных. В технике, скажем при управлении космическими аппаратами, будет перерасход горючего и увеличится время выполнения задания. А в анимационном фильме его герои предстанут комично-роботизированными существами с неестественными движениями.
Кватернионы — это алгебраические объекты, которые «приходят» из четырёхмерного мира и дают возможность представить движения точек мира трёхмерного как результат чисто арифметических действий с участием координат.
Вначале рассмотрим аналогичный, но более простой пример: задачу «алгебраизации» движений на плоскости.
Точки плоскости, т. е. пары вида $(a; b)$, «становятся» комплексными числами — традиционное обозначение $a+bi$ — после введения операций сложения (покоординатного) и умножения (в соответствии с таблицей умножения элементов базиса $\{1,i\}$). Элемент $i$, называемый мнимой единицей, оправдывает своё название тем, как ведёт себя его квадрат: $i^2=-1$. Оказывается, что параллельный перенос плоскости — это «прибавление» к каждому комплексному числу некоторого фиксированного комплексного числа, а поворот плоскости вокруг начала координат — умножение каждого комплексного числа на фиксированное число $a+bi$, у которого $a^2+b^2=1$ (модуль равен единице). Известно, что любое движение плоскости (не меняющее ориентации) является композицией параллельного переноса и поворота вокруг некоторой фиксированной точки (например, начала координат). Поэтому появляется возможность представления движений плоскости как алгебраических действий над комплексными числами. С этой точки зрения становится геометрически наглядной формула $i^2=-1$: умножение на $i$ — это поворот на угол $90°$, следовательно, $i^2$ переводит произвольную точку $z$ в $(-z)$, т. е. $i^2z=-z$, или $i^2=-1$.
Великий российский математик и замечательный популяризатор науки Владимир Игоревич Арнольд и на лекциях, и в книгах подчёркивал важность геометрического понимания такого подхода. Он писал: «Комплексные числа — математический аппарат для описания движений плоскости».
Одним из создателей теории комплексных чисел был ирландский математик Уильям Гамильтон. Следующим шагом стала естественная попытка «превратить в числа» и точки трёхмерного пространства так, чтобы эти «числа» играли в трёхмерной геометрии ту же роль, что и комплексные числа на плоскости.
Несмотря на многолетние усилия, такую теорию создать не удалось. Позднее было доказано, что в трёхмерном мире это в принципе невозможно.
Но размышления над трёхмерной задачей не были бесплодными: они привели Гамильтона к решению проблемы для четырёхмерного пространства — к созданию теории кватернионов.
Формально кватернион — это четвёрка действительных чисел $(a; b; c; d)$, которую по традиции записывают в виде $q = a + bi+ cj + dk$. Эту запись можно воспринимать как разложение четырёхмерного вектора по базису $\{1, i, j, k\}$ (в отличие от комплексных чисел, здесь одна «обычная» единица и целых три мнимых!). Кватернионы можно складывать — покоординатно. А если удастся придумать согласованные правила умножения базисных векторов, то появится алгебра кватернионов.
Таблица умножения мнимых базисных кватернионов и есть открытие Гамильтона. Главным условием согласованности, корректности правил умножения является цепочка формул $i^2=j^2=k^2=ijk=-1$, которая впервые была нацарапана Гамильтоном на каменном мосту в Дублине. Правило чтения таблицы: в клетке стоит произведение элемента из строки на элемент из столбца, например, $ij=k$, $ji=-k$. Видно, что произведение кватернионов зависит от порядка сомножителей.
Именно это непривычное свойство кватернионов объединяет их с движениями в трёхмерном пространстве. Но чтобы использовать это сходство, сопоставить кватернионы движениям, придётся сделать ещё один шаг — «выйти» из нашего трёхмерного мира в четырёхмерный.
Оказывается, если обычную точку $(x;y;z)$ записать как мнимый кватернион $p=(0;x;y;z)$, то параллельный перенос точки описывается сложением с фиксированным мнимым кватернионом, а поворот связан с умножением $p$ на кватернион, в координатах которого «заложена» информация об оси и угле поворота (вспомним теорему Эйлера!). В обоих случаях $p$ переходит в чисто мнимый кватернион, три последние координаты которого — координаты точки, в которую переводит точку $(x;y;z)$ данное движение.
Описание последовательности движений сводится к выполнению цепочки алгебраических действий над кватернионами. Выполнение двух переносов (их «сумма») — это добавление суммы соответствующих кватернионов. Если $q_1$ и $q_2$ — кватернионы, сопоставленные двум вращениям, то произведение $q_2q_1$ будет задавать композицию этих вращений, их «произведение». В свою очередь, алгебраические операции с кватернионами — простые, так как сводятся к чисто арифметическим действиям с их компонентами, обычными числами.
Одно из важных преимуществ кватернионов перед углами Эйлера — на этом языке легко найти и описать оптимальную траекторию для изменения ориентации тела в пространстве.
В статье были отмечены проблемы, возникающие при описании вращений в трёхмерном пространстве тремя параметрами. Кватернионы предлагают четыре параметра, и этого достаточно для практических применений. Но математически корректным кватернионное представление не является: одному повороту соответствует два кватерниона — нет однозначности. Только в середине XX века было доказано, что пяти параметров достаточно для корректной параметризации вращений в трёхмерном пространстве.
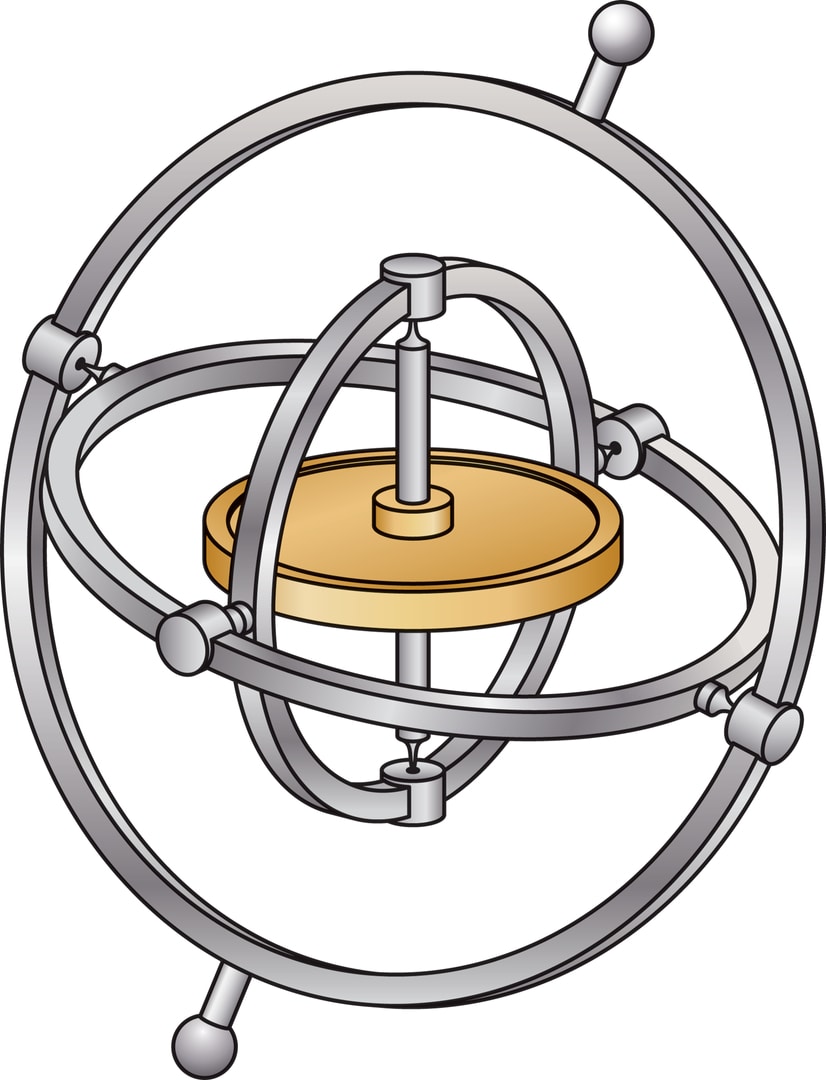
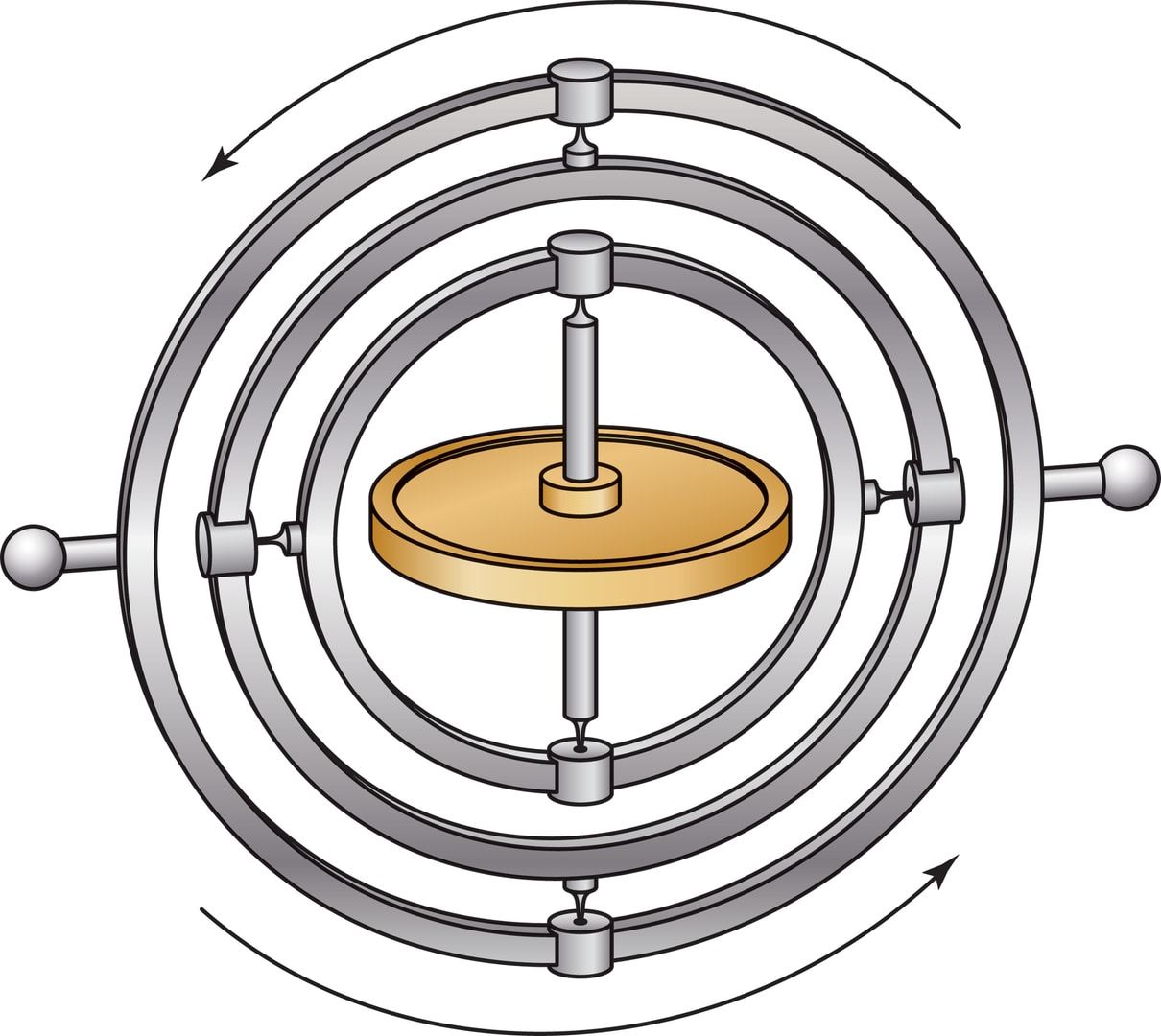
Для решения задач управления движением используют гироскопы (соединение древнегреческих слов γῦρος — круглый и σκοπέω — смотрю). В классическом гироскопе двумя основными составляющими являются карданов подвес и закреплённый в нём быстро вращающийся маховик (скорость может составлять и 500 оборотов в секунду).
Согласно одной из теорем Эйлера, раскрученный маховик стремится сохранить направление оси вращения. Именно поэтому сохранять равновесие на движущемся велосипеде проще, чем на неподвижном, а при большой скорости можно даже не держаться за руль. Почувствовать теорему позволяет известный опыт. Раскрутив колесо, насаженное на длинную ось со втулками, и взявшись за них, вы ощутите, что попытка изменить положение оси вызовет сопротивление колеса, оно будет «упираться».
Карданов подвес — это три вложенные друг в друга рамки-кольца, соединённые осями: внешняя рамка крепится осью к движущемуся аппарату, а ось маховика крепится к внутренней рамке. Такой подвес позволяет раскрученному маховику сохранять направление оси вращения при любых движениях аппарата.
Ориентацию корабля, самолёта или космического аппарата определяют по положению объекта относительно «неподвижной» оси вращения гироскопа. Информация складывается из трёх параметров — углов между осью маховика и осями рамок.
Упомянутая в статье опасность «складывания рамок» соответствует ситуации, когда внутренняя и внешняя рамки карданова подвеса оказываются в одной плоскости. Их оси в такой момент тоже совпадают, и у конструкции теряется одна степень свободы. Ось гироскопа оказывается в плоскости внешней рамки и не сможет сохранять направление при некоторых движениях объекта. Например, при вращении аппарата в плоскости сложенных рамок придётся повернуться и оси маховика — утрачена способность сравнивать текущую ориентацию с начальной (стартовой).
Проблема «складывания рамок» проявилась и в лунной миссии «Аполлон‐11». Во время полёта возникла ситуация, близкая к критической, и хотя всё обошлось, после возвращения один из астронавтов в шутку попросил у коллеги из ЦУПа четвёртый параметр: «Как насчёт того, чтобы подарить мне на Рождество четвёртую рамку?».
Арнольд В. И. Геометрия комплексных чисел, кватернионов и спинов. — М.: МЦНМО, 2014.
Конвей Дж., Смит Д. О кватернионах и октавах, об их геометрии, арифметике и симметриях. — М.: МЦНМО, 2019.
Полак Л. С. Уильям Гамильтон: 1805—1865. — М.: Наука, 1993.
Бранец В. Н., Шмыглевский И. П. Применение кватернионов в задачах ориентации твёрдого тела. — М.: Наука, 1973. — [Для специалистов в области систем управления движением летательных аппаратов].