Передача равномерного вращательного движения с одной оси на другую — одна из основных задач в теории механизмов. В наручных часах важна точность преобразования угловых скоростей, в «серьёзных» машинах необходимо передавать и силовые функции.
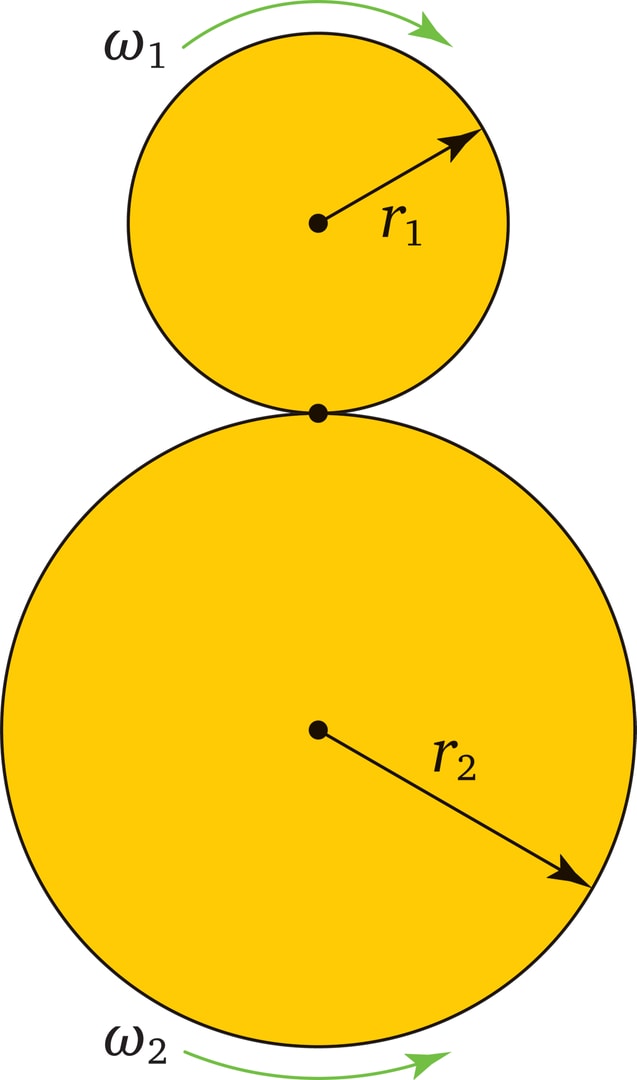
Наглядный способ решения задачи — два касающихся диска, служащих «передаточными» звеньями от их осей. В идеальной модели, при отсутствии проскальзывания, второй диск тоже будет вращаться равномерно. Отношение угловых скоростей дисков будет обратно пропорционально отношению радиусов: $\frac{\omega_1}{\omega_2}=\frac{r_2}{r_1}$ (так как в точке соприкосновения совпадают линейные скорости: $r_1\omega_1=r_2\omega_2$).
Но в реализации такой модели проскальзывание устранить не удаётся. Превращение дисков в зубчатые шестерёнки — техническое решение проблемы. Его можно рассматривать как модификацию наглядной схемы с касающимися кругами.
Зубья двух шестерёнок должны друг другу соответствовать, хотя их форма может быть и различной. Во‐первых, для передачи равномерности движения необходимо, чтобы контакт (зацепление) между зубчатыми колёсами ни на миг не прерывался. Во‐вторых, трение между зубьями должно быть минимальным, чтобы уменьшить износ деталей. Второе требование не является абсолютным, поскольку ещё Леонард Эйлер в 1752 году доказал, что при передаче равномерного движения добиться полного отсутствия трения скольжения невозможно.
В 1762 году Эйлер предложил использовать в зубчатых передачах эвольвентное зацепление, оказавшееся весьма удачным и ставшее самым распространённым, в основном, в больших механизмах.
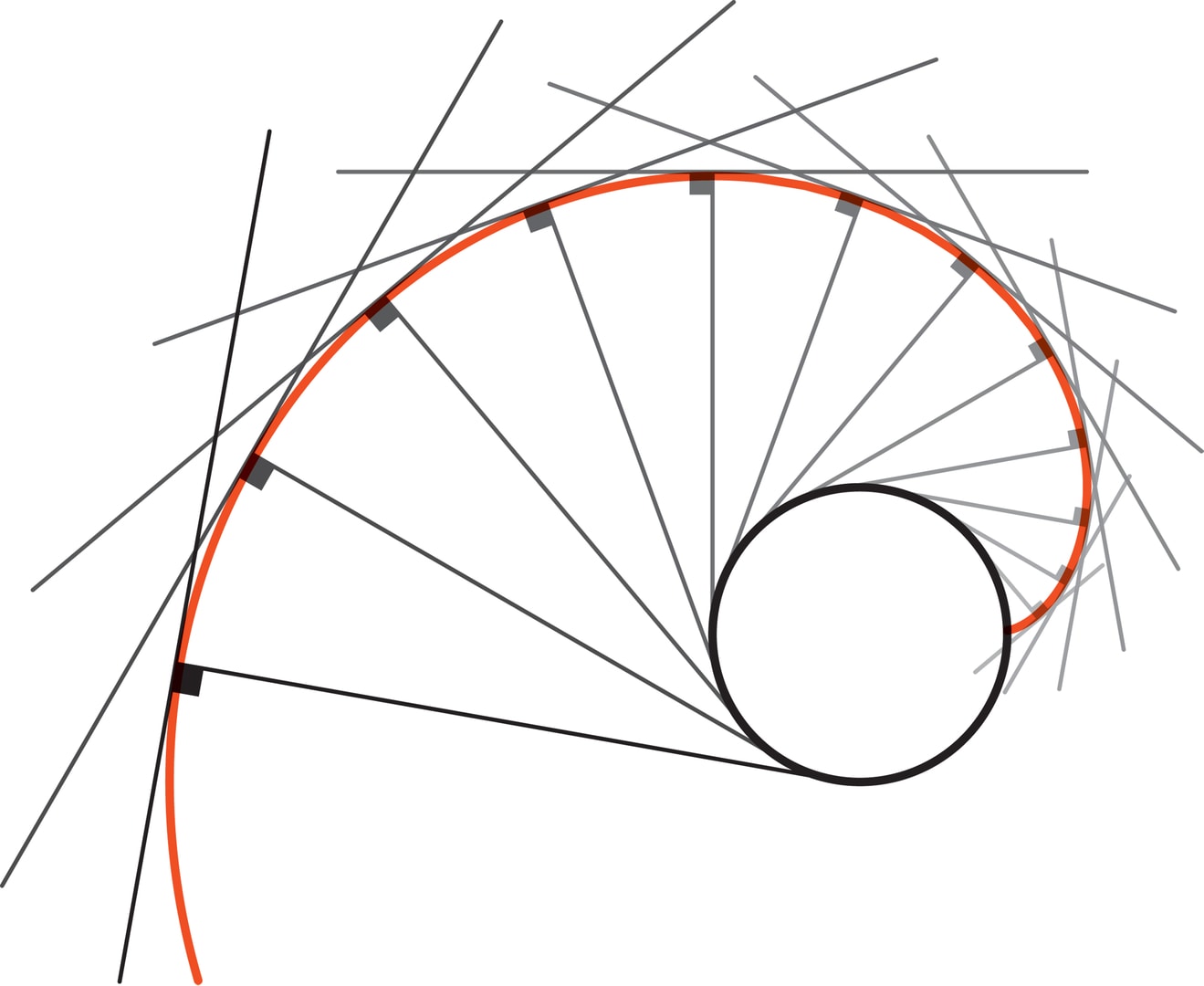
Эвольвента окружности — кривая, которую описывает конец натянутой нити, сматываемой с диска. В этом эксперименте можно «увидеть» и эвольвенту, и главное для нас геометрическое свойство: при сматывании в каждый момент времени нить будет касательной к окружности и перпендикулярна эвольвенте.
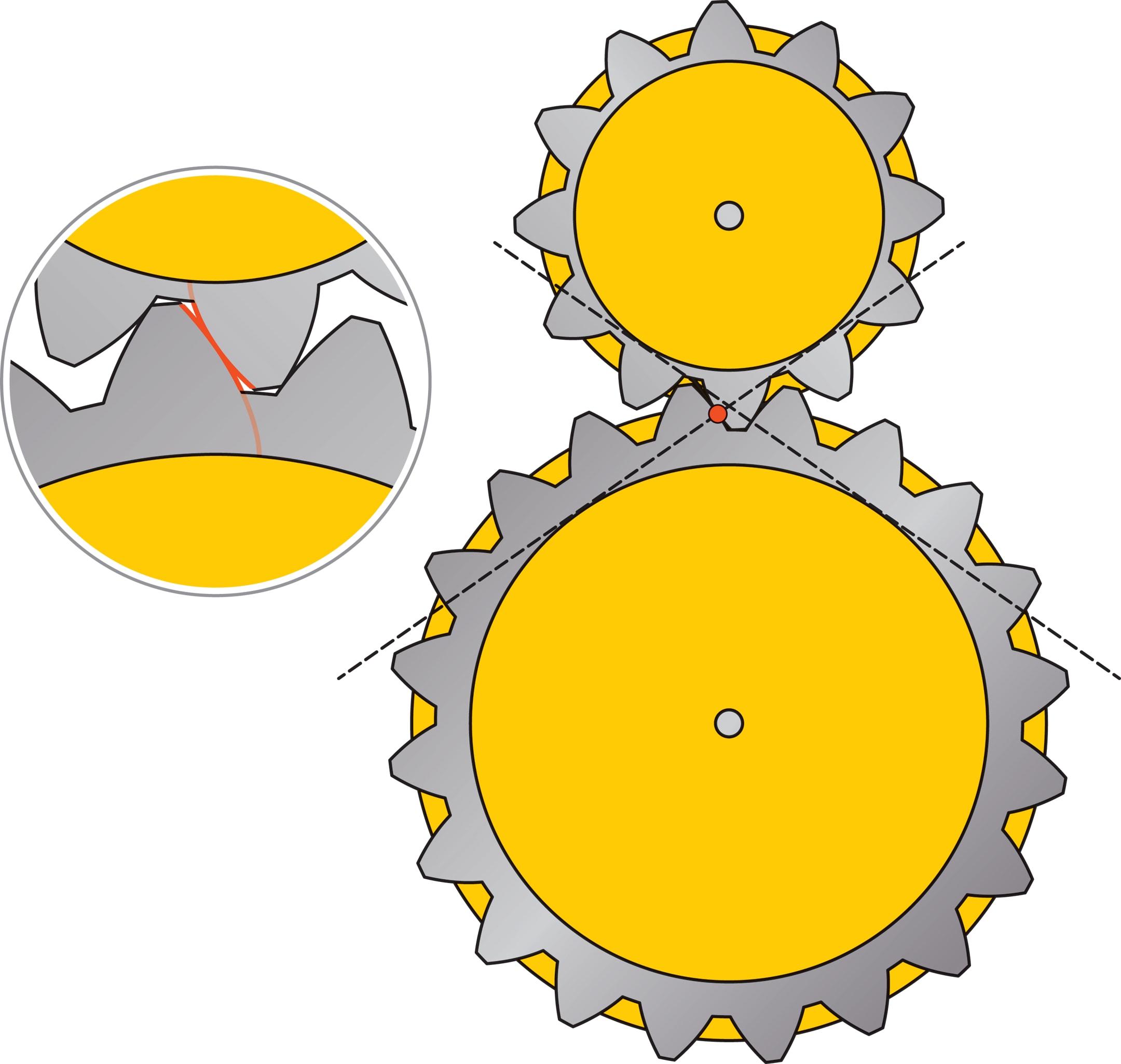
Для «изготовления» пары работающих шестерёнок с зубьями эвольвентного профиля уменьшим пропорционально радиусы двух касающихся кругов, а получившиеся меньшие круги «оснастим» зубьями, форма которых определяется эвольвентами малых окружностей. Во время взаимного обкатывания двух зубьев (эвольвент) разных шестерёнок точка их касания бежит по общей касательной малых окружностей. В каждый момент времени эта касательная будет перпендикулярна в точке соприкосновения зубьев каждому из них: это следует из приведённого геометрического свойства. Следовательно, передача движения будет происходить вдоль касательной, малые колёса с зубьями взаимодействуют так, словно это касающиеся диски. «Касательное» взаимодействие шестерёнок означает, что в их соприкосновении нет отталкивания, энергия тратится на передачу вращения. Трение между зубьями есть, но невелико.
Другой популярный тип шестерёнок — с циклоидальными зубьями. «Механическое» определение циклоиды: траектория точки на ободе колеса, которое катится по прямой. Эпициклоида и гипоциклоида, определяющие профили зубьев циклоидального зацепления: траектория точки на ободе колеса, которое катится по другой окружности снаружи (эпициклоида) или изнутри (гипоциклоида). Циклоидальные профили чаще встречаются в часовых механизмах.
У зацеплений различных типов есть свои преимущества. Для эвольвентного зацепления можно выделить: простоту изготовления профилей зубьев по методу обкатки, что повышает их прочность; изношенные колёса легко заменить новыми, любые два подходят друг к другу. Превосходство циклоидального зацепления, например, в том, что коэффициент перекрытия колёс больше, это позволяет использовать шестерёнки с небольшим числом зубьев.
В передачу равномерного вращательного движения шестерёнки вносят «рациональное» начало: отношение радиусов равно отношению чисел зубьев на шестерёнках (передаточное отношение).
В рассмотренных конструкциях считалось, что оси параллельны; «наглядные» цилиндры служили заготовкой, основой для конструирования шестерёнок. Но зубчатые передачи служат и в других ситуациях. Если оси пересекаются (что часто встречается в технике), то место цилиндров занимают конусы, если оси скрещиваются — гиперболоиды. А профили зацеплений становятся ещё более замысловатыми.