В далёкой древности было замечено, что поверхность Земли не является плоской. Об этом говорило, например, такое наблюдение: когда на горизонте появляется корабль, то сначала видны верхушки мачт, и только потом появляется весь парусник. Предположение, что форма Земли — шарообразная, возникло незадолго до Пифагора. Экспериментальное подтверждение гипотезы принадлежит, видимо, Аристотелю, приводившему следующий довод. Во время лунного затмения меняющаяся граница тени Земли в каждый момент времени является дугой окружности, а только у шара граница тени при всех проекциях круговая.
Но планета — только часть трёхмерного пространства, «живущего» в четырёхмерном пространстве-времени. И в XX веке физики пришли к выводу, что фундаментальный вопрос о природе тяготения можно объяснить если связать его с кривизной пространства.
Чтобы читатель смог подойти к понятию кривизны в многомерном пространстве, рассмотрим с разных точек зрения «привычную» кривизну поверхности. На страницах книги это понятие встречалось в сюжетах «Ломтик пиццы» и «Футбольный мяч». Во многих случаях, в том числе и в утверждении о невозможности создания плоской карты Земли без искажений («Картографические проекции»), основную роль играет теорема Гаусса о кривизне.
Начнём разговор с прямого, полученного Эйлером в середине XVIII века ещё до появления теоремы Гаусса, объяснения того, что даже небольшой участок сферы не картографируется без искажений на плоскую область, т. е. его нельзя отобразить на плоскость так, чтобы сохранялись длины всех линий (а следовательно, и площади областей). Для этого достаточно проследить за «судьбой» окружности небольшого радиуса (её длиной, кругом, который она ограничивает, и его площадью).
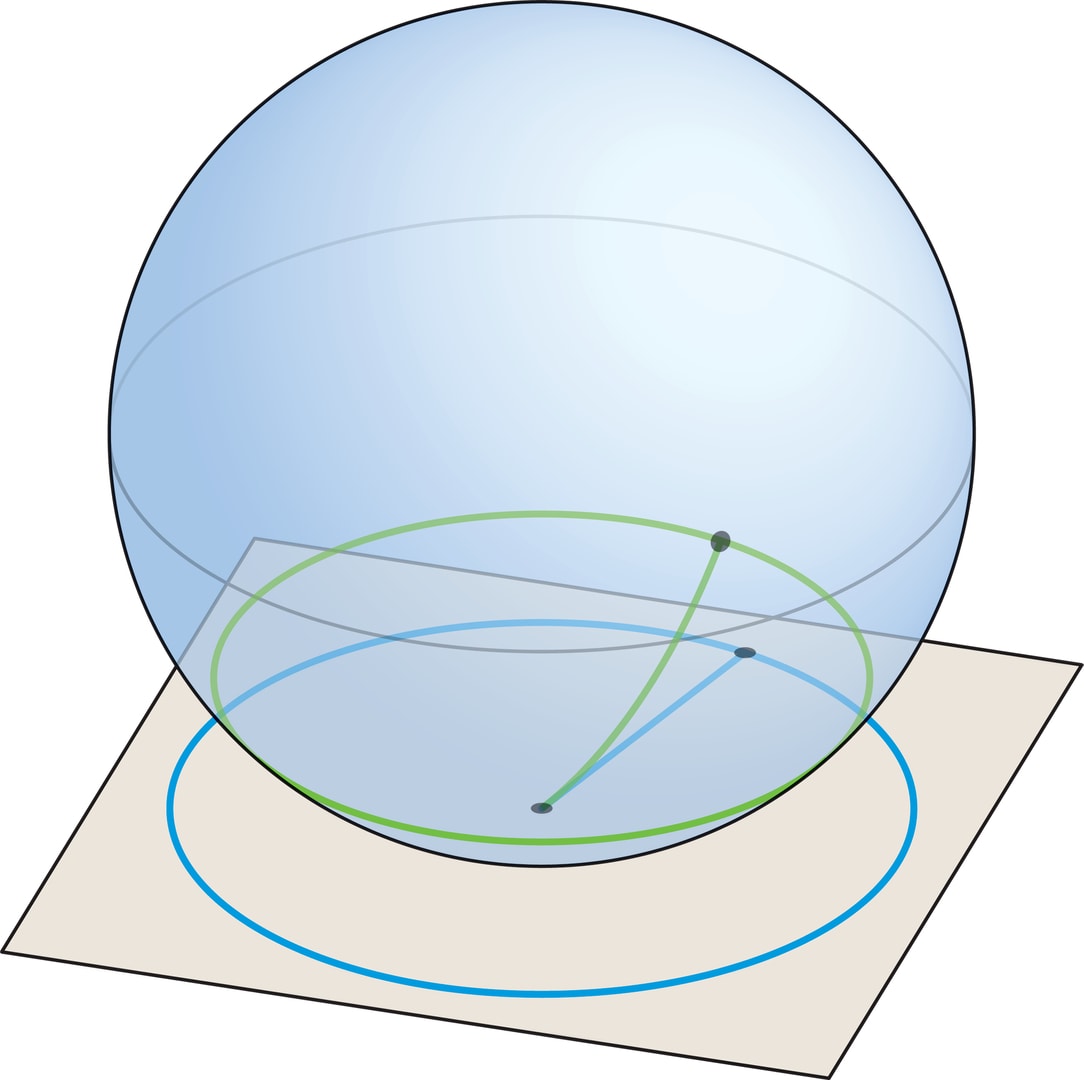
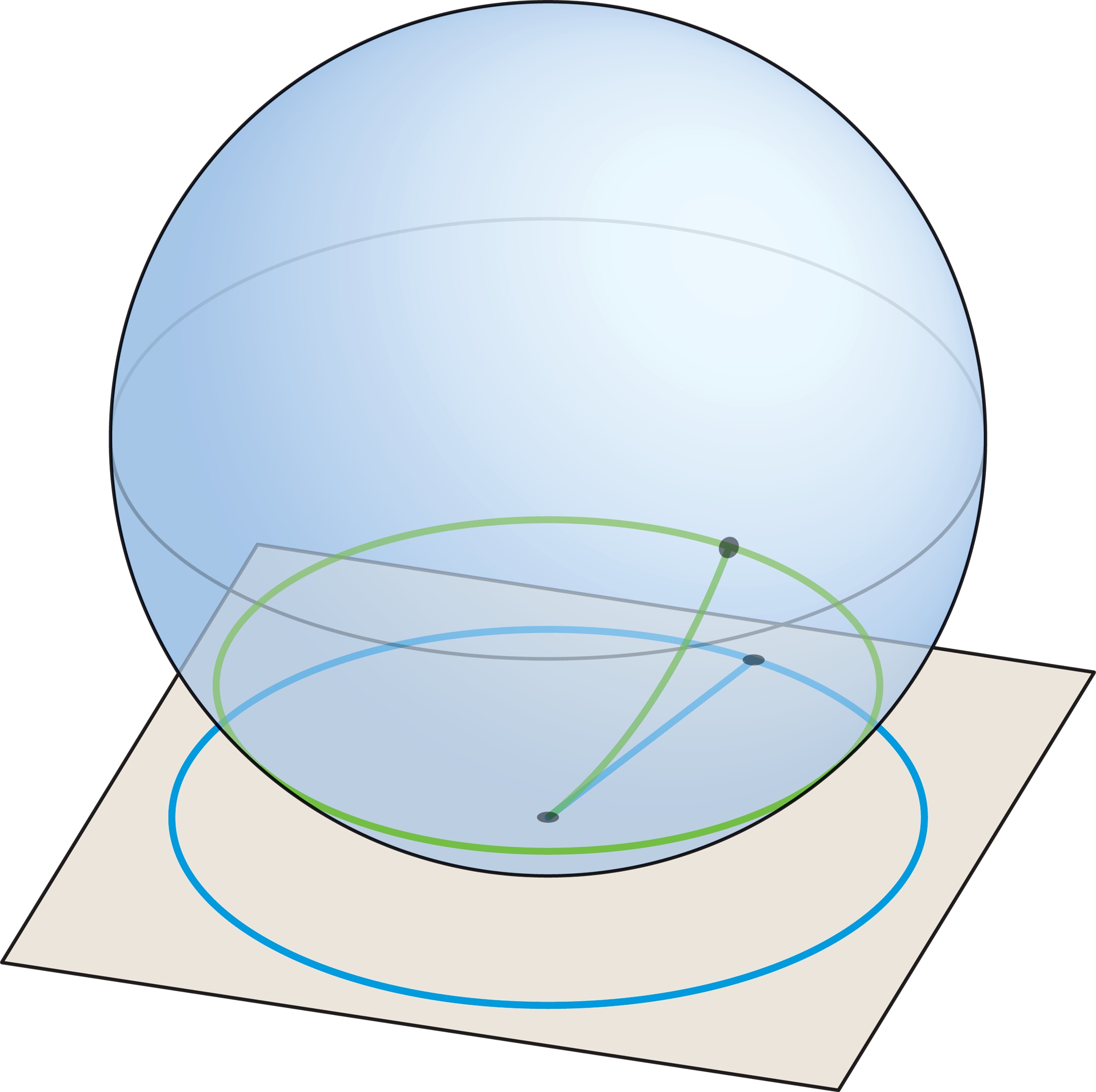
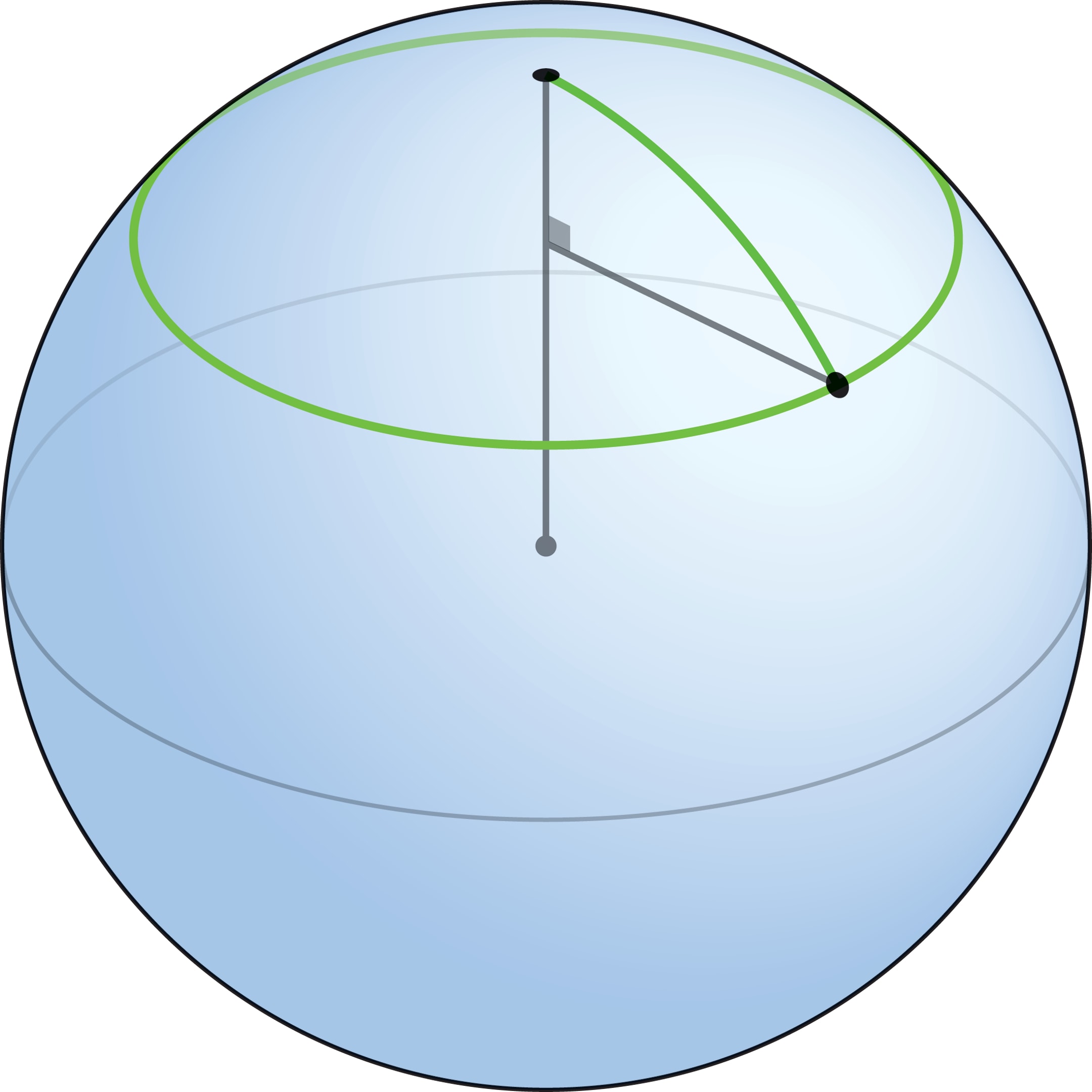
На плоскости кратчайший путь, соединяющий пару различных точек, — отрезок прямой. Точки, которые отстоят от заданной на расстояние $r$, образуют окружность радиуса $r$ с центром в данной точке. Чтобы узнать, как выглядят на сфере кратчайшие пути и множества точек, равноудалённых от данной, проведём геометрический эксперимент.
На плоскости окружность радиуса $r$ можно нарисовать с помощью натянутой нити длины $r$, один конец которой закреплён. На глобусе, закрепив один конец достаточно короткой нити в полюсе и натянув её вдоль поверхности, получим отрезок меридиана. Длина этого отрезка — кратчайшее расстояние между точками, в которых оказались концы нити. Всевозможные положения незакреплённого конца натянутой нити составляют одну из параллелей на глобусе, это и есть множество точек, равноудалённых от полюса на расстояние, равное длине нити.
Параллель состоит из точек, удалённых на расстояние $r$ от данной, поэтому должна перейти в окружность радиуса $r$ на плоскости (такая окружность определяется распрямлением нити). Но длины должны сохраняться не только вдоль меридианов, в частности, длина параллели должна равняться длине её образа — окружности радиуса $r$, а это, очевидно, не так.
Уточним это экспериментальное доказательство с помощью аналитических формул. Из них мы увидим, как искажение длины «окружности» на сфере связано с понятием кривизны.
Расстояние между двумя точками на поверхности определяется как наименьшая из длин кривых, соединяющих эти точки и лежащих на этой поверхности. Это определение аналогично определению расстояния между точками на плоскости. На плоскости кратчайшей кривой является отрезок, соединяющий точки. На сфере кратчайшая кривая между двумя точками — это меньшая дуга большой окружности, которая получается в пересечении сферы с плоскостью, проходящей через эти точки и центр сферы.
Большие окружности на сфере и прямые линии на плоскости являются примерами геодезических. Так называются линии, у которых все достаточно короткие отрезки являются кратчайшими путями, соединящими их концы. Например, на сфере единичного радиуса большие окружности являются геодезическими, но кратчайшими путями между их концами являются дуги длины, не большей, чем $π$. Заметим, что две противоположные точки на сфере связаны бесконечным числом кратчайших линий — отрезков меридианов.
Множество точек на сфере, равноудалённых от данной точки $P$ на расстояние $r$, естественно назвать окружностью (с центром в точке $P$ и радиуса $r$). В геометрии окружающего трёхмерного пространства — это параллель $Z_r$, которая получается при пересечении сферы с плоскостью, т. е. обычная окружность. Отметим, что если $R$ — радиус сферы, то с ростом $r$ от 0 до $π R/2$ (до «экватора») «физические» размеры параллели $Z_r$ увеличиваются, а с дальнейшим увеличением $r$ начинают уменьшаться и при $r=π R$ окружность превращается в точку. Употребление слова «параллель» не на глобусе, а на сфере оправдано «равноправием» её точек. При вращении сферы вокруг её центра сферические расстояния между точками не меняются, а в выделенную точку «полюс» таким преобразованием можно перевести любую точку.
Вернёмся к основной задаче и ответим на вопрос, почему нельзя без искажений картографировать поверхность глобуса на плоскую область.
Например, если бы небольшую круглую шапочку, окружающую полюс на глобусе, можно было «точно» картографировать на плоскость, то образом граничной параллели $Z_r$ была бы обычная окружность радиуса $r$ на плоскости. При этом точность картографирования должна была бы обеспечить совпадение длин путей и, как следствие, площадей областей. Сравним длины линий в паре «параллель—окружность» и площади в паре «шапочка—круг».
На плоскости длина окружности радиуса $r$ и площадь ограниченного ею круга равны соответственно $$ \ell(r)=2π r, \qquad S(r)=π r^2. $$
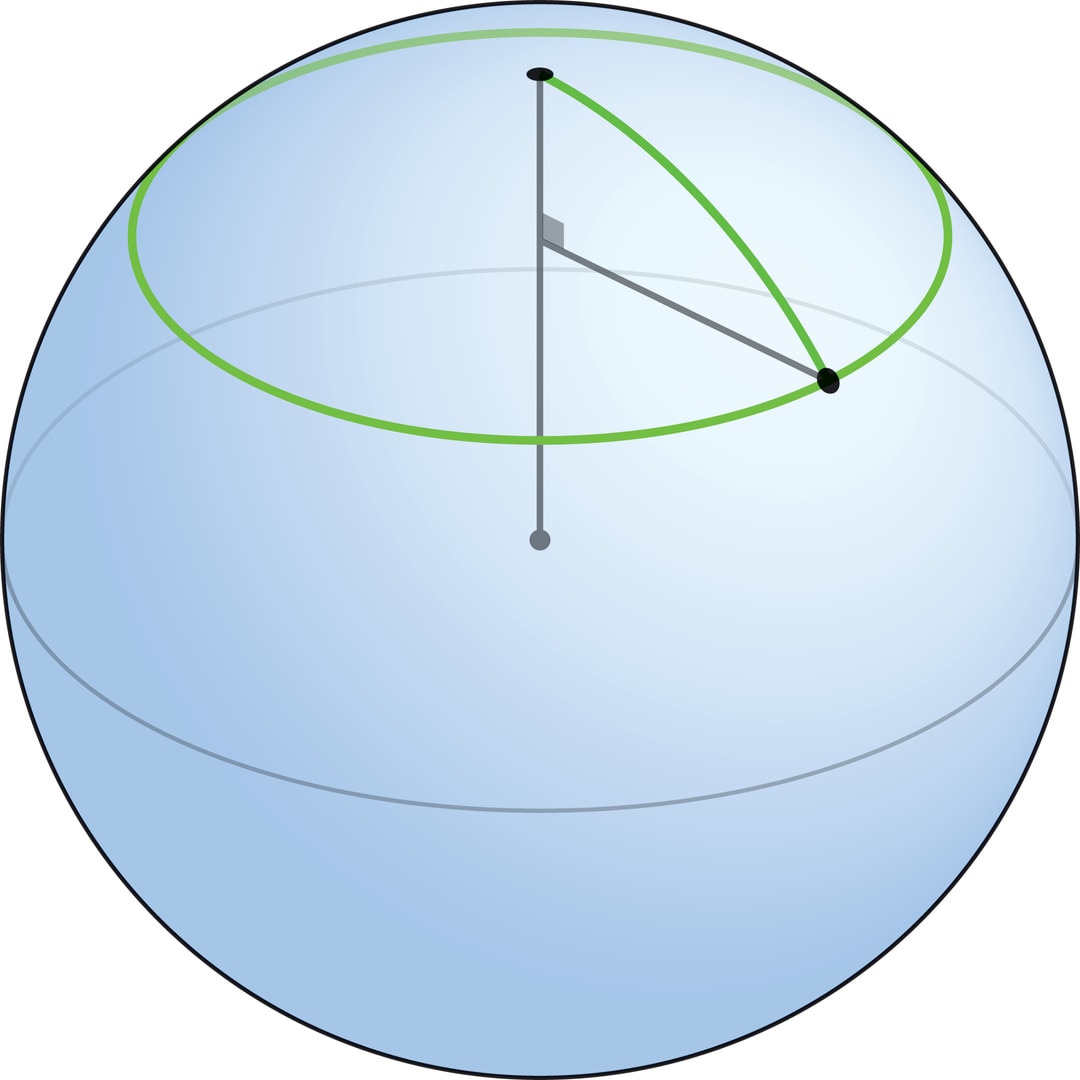
Окружности радиуса $r$ на плоскости соответствует на сфере параллель $Z_r$ — окружность, радиус которой равен $R\sin α$ (где $α$ — угол между осью и образующими конуса, который получается, если провести радиусы к точкам на параллели $Z_r$).
Длина параллели и площадь части сферы, которую она ограничивает, равны $$ \skew4\tilde \ell (r)=2π R \sinα, \qquad \tilde S(r)= 2(1-\cosα) \>π R^2. $$
Первая из формул — просто длина окружности радиуса $R\sin α$. Вторую формулу можно получить, если вспомнить, что площадь поверхности шара равна $4π R^2$, и если решить задачу о том, какую часть поверхности сферы вырезает конус с вершиной в её центре и углом при вершине конуса, равным $2α$.
Углу $α$ можно дать и другое толкование: это центральный угол в окружности радиуса $R$, опирающийся на дугу длины $r$. Следовательно, по определению радианной меры $α=\frac{r}{R}$. При малых значениях $α$ ($r\ll R$) $$ \sinα≈ α- \frac16α^3, \qquad \cosα≈ 1- \frac12α^2 + \frac{1}{24}α^4. $$
Подставив эти приближённые значения в формулы для $\skew4\tilde \ell (r)$ и $\tilde S(r)$, получим $$ \skew4\tilde \ell (r) ≈ 2π R {\left(α - \frac{α^3}{6}\right)} =2π r - \frac{π}{3R^2} r^3, \qquad \tilde S(r)≈ π r^2 - \frac{π}{12R^2}r^4. $$
Видно, что $\ell(r) \ne \skew4\tilde \ell (r)$ и $S(r) \ne \tilde S(r)$ даже при малых значениях $r$. Поэтому никакой сколь угодно малый участок сферы нельзя отобразить на плоскость с сохранением длин и площадей.
При малых значениях $r$ в первом приближении длины окружностей и площади кругов совпадают с их аналогами на сфере, а в поправки входит кривизна сферы: $$ \skew4\tilde \ell (r) ≈ \ell (r) - \frac{π K}{3} r^3, \qquad \tilde S(r)≈ S(r) - \frac{π K}{12}r^4, $$
где $K=\frac{1}{R^2}$ — гауссова кривизна сферы.
В общем случае гауссова кривизна зависит от точки поверхности. Поверхностями постоянной кривизны, например, являются сферы — для них кривизна в каждой точке равна $\frac1{R^2}$, а также плоскости — в этом случае кривизна в каждой точке равна нулю.
Ещё одну трактовку кривизны даёт сравнение треугольников на плоскости и в сферическом мире. Например, отличие сферы (как и любой другой «кривой поверхности») от плоскости проявится, если сравнить на этих поверхностях результаты параллельного переноса вектора вдоль замкнутого пути.
Параллельный перенос вектора из одной точки в другую вдоль геодезической реализуется семейством векторов, приложенных ко всем точкам отрезка геодезической так, что их длины и угол между векторами и геодезической сохраняются. (В начальной точке вектор семейства совпадает с данным вектором.)
Для плоскости это определение совпадает с обычным «школьным» определением параллельного переноса. При переносе вектора вдоль сторон треугольника он перейдёт сам в себя. Но в искривлённом пространстве, например на сфере, это уже не так.
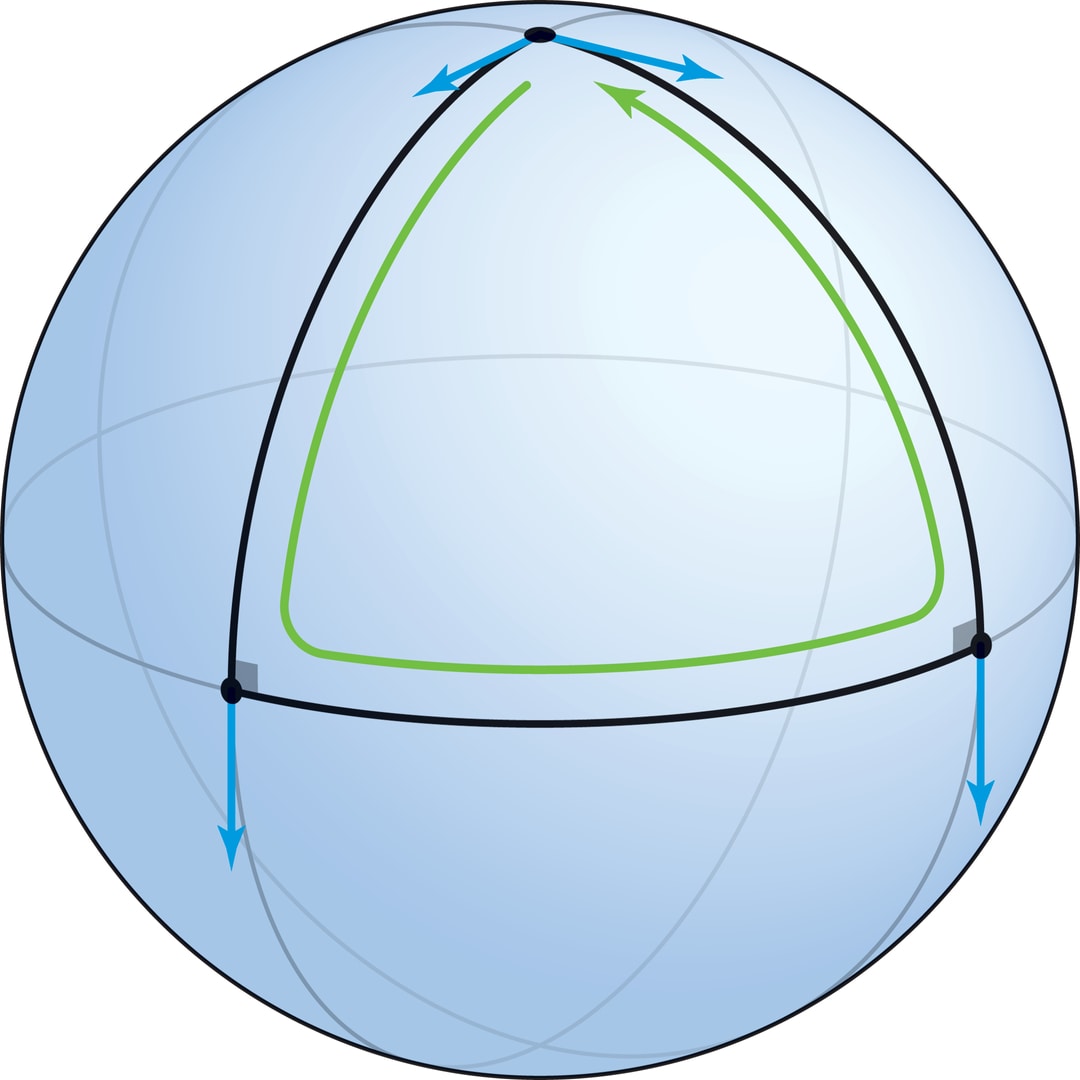
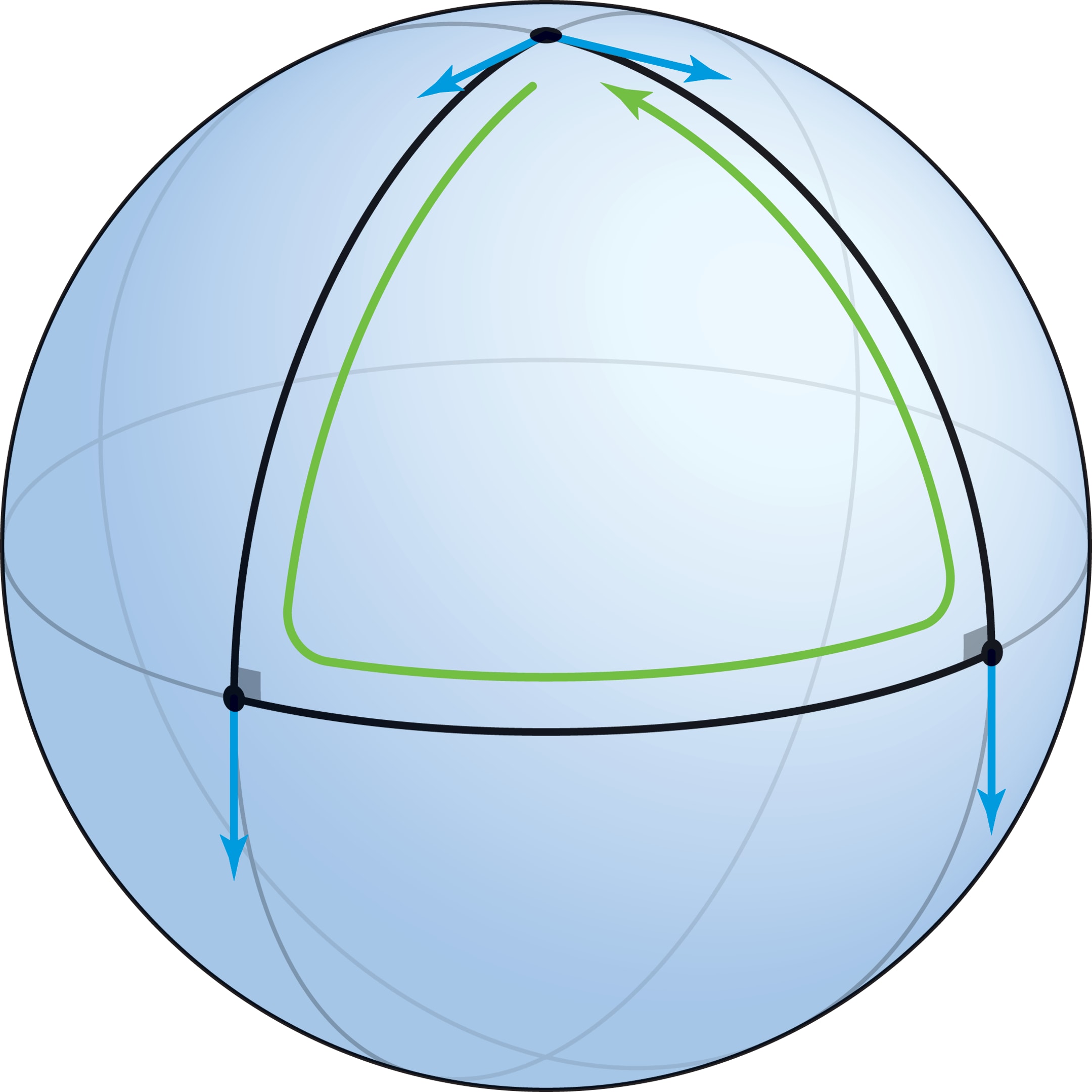
Сферическим треугольником называется фигура, ограниченная дугами трёх больших окружностей (стороны треугольника — отрезки геодезических, кратчайшие пути, соединяющие вершины). Рассмотрим треугольник, ограниченный двумя меридианами, выходящими из полюса под углом $α$, и вырезаемым ими отрезком экватора. Вектор (ненулевой), выходящий из полюса вдоль стороны треугольника, после параллельного переноса вдоль меридиана в вершину на экваторе окажется перпендикулярен плоскости экватора. При переносе вдоль экватора в следующую вершину перпендикулярность вектора экваториальной плоскости сохранится, а после параллельного переноса вдоль меридиана в полюс получим вектор, направленный вдоль этого меридиана. Полученный вектор отличается от исходного (они образуют угол $α$), в этом несовпадении проявляется кривизна сферы.
В рассмотренном треугольнике сумма углов равна $\frac{π}{2}+\frac{π}{2}+α=π+α$, т. е. больше, чем $π$ (это в радианной мере, а в градусной получается, что сумма углов больше $180°$). В частности, эта конструкция при $α=\frac{π}{2}$ даёт пример треугольника на сфере с тремя прямыми углами.
Отталкиваясь от того, что площадь поверхности сферы радиуса $R$ равна $4π R^2$, можно найти площадь рассмотренного треугольника: $S(α)=α R^2$. Гауссова кривизна сферы постоянна, $K=\frac{1}{R^2}$. С помощью этих соотношений для суммы углов этого треугольника получается формула $π+α=π+K\>S(α)$, т. е. гауссова кривизна и здесь выступает как мера отличия поверхности от плоскости. Это частный случай формулы Гаусса—Бонне, позволяющей даже на поверхности с кривизной, меняющейся от точки к точке, связать отклонение суммы углов треугольника от $π$ с гауссовой кривизной.
В евклидовой геометрии через точку, лежащую вне заданной прямой, можно провести прямую, параллельную данной, и притом только одну. В этом состоит аксиома о параллельных прямых (она ещё известна как «пятый постулат» Евклида). Отрицать аксиому Евклида можно двумя способами: либо утверждать, что через точку не проходит ни одна параллельная прямая, либо — что проходит несколько параллельных прямых.
Первый вариант реализуется в сферической геометрии: аналоги прямых — большие окружности (геодезические). Любая пара таких линий пересекается в двух точках, т. е. параллельных «прямых» нет. Но надо отметить, что в сферической геометрии нарушается ещё более важный принцип — единственность прямой, проходящей через две точки. На сфере через диаметрально противоположные точки проходит бесконечно много «прямых» — больших окружностей.
Другая форма отказа от постулата о параллельных прямых стала основой геометрии, теоретически построенной Николаем Ивановичем Лобачевским. (Первые примеры пространств, в которых геометрия Лобачевского реализуется, были найдены только через сорок лет после первых работ Лобачевского о «воображаемой геометрии».)
Лобачевский вывел все аналитические формулы новой теории, оснастил её вычислительными инструментами. Оказалось, что если понимать под треугольниками фигуры, составленные из трёх отрезков геодезических, то возникают нетривиальные соотношения между длинами сторон и углами треугольников, которых нет в евклидовой геометрии. В частности, сумма углов треугольника всегда меньше, чем $π$ (в сферической геометрии — больше, чем $π$).
Французский математик Лежандр, пытаясь вывести постулат о параллельных из других аксиом Евклида, доказал, что если существует хотя бы один треугольник с суммой углов, равной $π$, то постулат о параллельных выполняется.
Аналоги рассмотренных на сфере функций $\skew4\tilde \ell (r)$ и $\tilde S(r)$ в геометрии Лобачевского выглядят точно так же, как в сферической геометрии, только вместо тригонометрических функций появляются гиперболические (геометрию Лобачевского часто называют гиперболической). Вид приближённых формул для $\skew4\tilde \ell (r)$ и $\tilde S(r)$ тоже сохраняется, надо только учесть, что гауссова кривизна в этой геометрии отрицательная: $K<0$.
Правильное обобщение кривизны на многомерные пространства основано на понятии параллельного переноса. Мы уже продемонстрировали, что на круглой (обычной) сфере такой перенос вектора вдоль замкнутого пути, вообще говоря, не переводит его в себя, а различие двух векторов связано с кривизной сферы.
В современной физике одно из основных положений состоит в том, что сила тяготения (притяжения), физическое взаимодействие, по сути есть геометрическая характеристика нашего пространства — его кривизна.