Источником звука могут служить музыкальные инструменты различных типов (струнные, духовые и др.), но с точки зрения математики все способы извлечения звука можно представить с помощью одной, общей для всех них модели — колебаний струны.
Модельным устройством генерации звука можно считать монохорд, в древности служивший не только научным прибором, но и музыкальным инструментом. Монохорд — это деревянный резонатор, над которым натянута струна, закреплённая в двух точках. Длину звучащей части струны можно менять с помощью передвигающейся подставки.
Было установлено, что при неизменных характеристиках струны (материал, натяжение) частота её колебаний обратно пропорциональна длине ($f\sim 1/\ell$). Частота — главная математическая характеристика звука, определяющая его восприятие человеком на слух. Получается, что уменьшение длины струны увеличивает частоту её колебаний и, следовательно, высоту звука. Громкость звука связана с другой характеристикой колебаний струны — амплитудой.
В музыке очень важно то, как воспринимает слушатель сочетания звуков. Простейший вариант — пара звуков (музыкальный термин — «интервал»). Опытным путём были найдены приятные для слуха так называемые чистые интервалы.
Например, можно проводить эксперименты с двумя одинаковыми монохордами, один из которых служит эталоном, а на втором — менять длину звучащей части струны.
К чистым интервалам относятся: унисон, октава, квинта, кварта (расположены по убыванию благозвучия). Перечисленные интервалы можно описать, приводя отношения длин струн монохордов, участвующих в эксперименте: унисон — длина добавочной струны равна длине эталонной, октава — отношение длины добавочной струны к длине основной равно 1/2, квинта — отношение равно 2/3, кварта — 3/4.
А поскольку частота колебаний струны обратно пропорциональна её длине, то приведённые интервалы можно описать так: у октавы частоты звуков отличаются в 2 раза, у квинты — отношение частот добавочной и эталонной струн равно 3/2, у кварты — 4/3.
Мы считали, что у колебаний струны есть только одна частота (в дальнейшем будем называть её основной), но так дело обстоит только в идеальной модели. В зависимости от свойств струны к основному звуку неизбежно добавляются дополнительные звуки — обертоны.
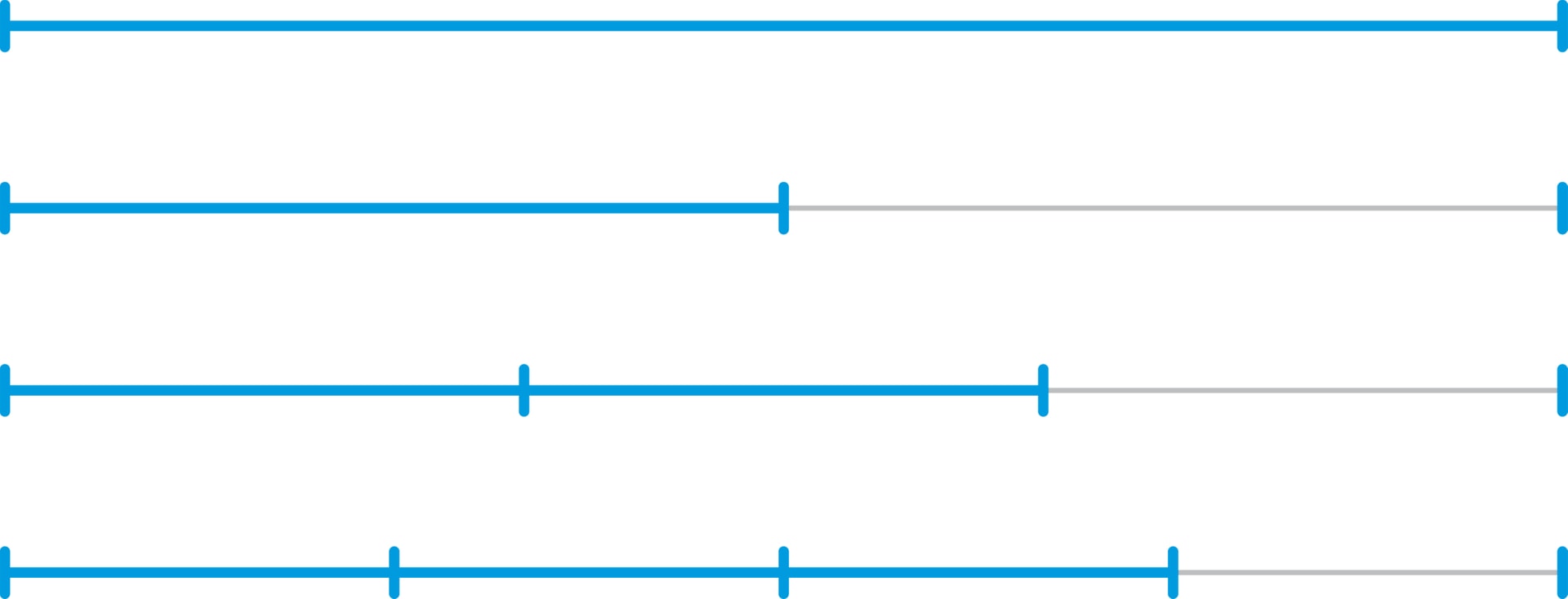
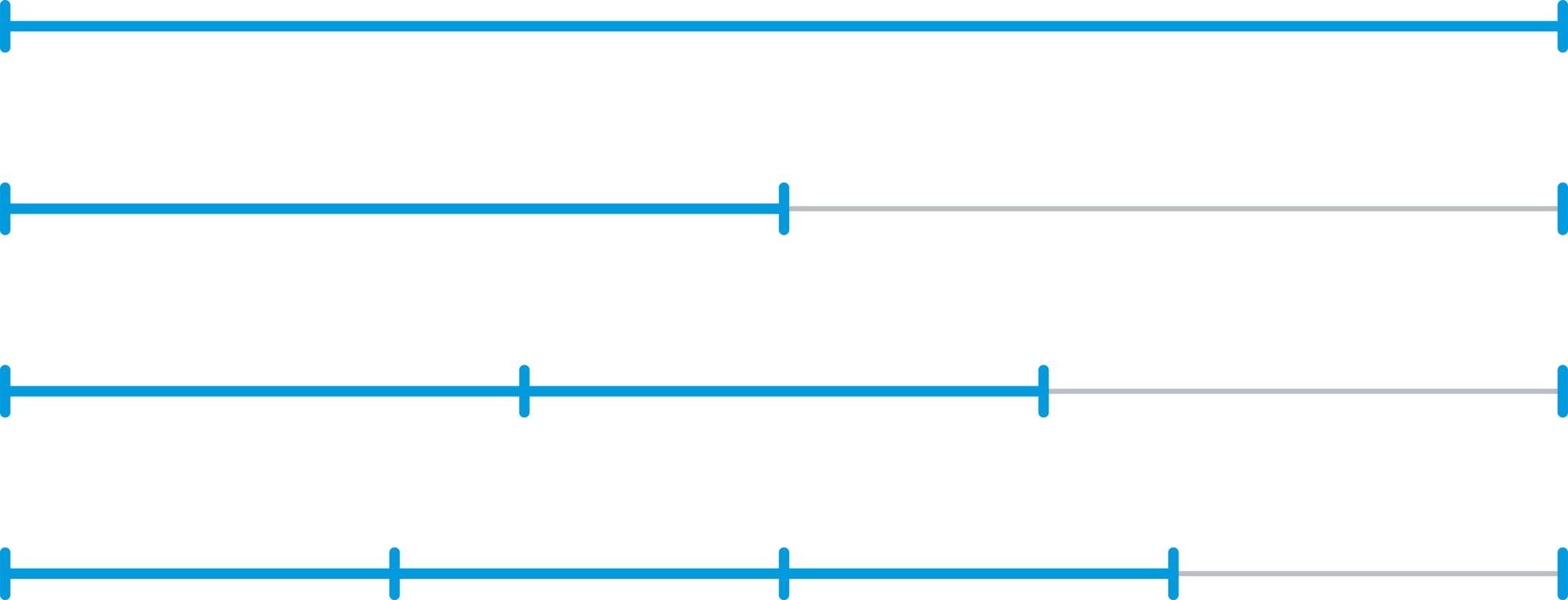
Наблюдаемые колебания струны с закреплёнными концами можно представить как результат наложения так называемых стоячих волн с незакреплёнными, но неподвижными точками (узлами) и однотипными колебаниями равных по длине участков между узлами.
Основной тон (определяемый значением $f$ — основной частотой струны) представляет стоячую волну без узлов, неподвижны только концы струны.
Первый обертон (т. е. первый «верхний тон») — стоячая волна с единственным узлом в середине струны. Фактически происходят колебания двух одинаковых струн половинной длины, частота колебаний этих «половинок» — $2f$. Второй обертон — стоячая волна с двумя узлами, которые делят струну на три равные части. Частота звука, порождаемого колебаниями каждой из трёх частей, втрое больше частоты полной струны.
В общем случае у обертона с номером $n$ имеется $n$ неподвижных узлов, которые делят струну на $(n+1)$ равных частей. Частота этого обертона равна $(n+1)f$. Полным набором частот реальной струны будет $\{f, 2f, 3f, 4f, …\}$.
Звучание струны, её тембр, складывается не только из набора частот, но и из соотношения громкостей обертонов. Громкости обертонов ниже, чем громкость основного тона, и убывают с возрастанием номера обертона. «Природная» согласованность основного тона и обертонов приводит и к согласованности совместного звучания, наилучшие результаты — у обертонов с небольшими номерами. Взаимодействие основного тона и обертонов оказывается полезным при изучении того, почему благозвучны, хотя и в разной степени, чистые интервалы. Можно предложить такое объяснение.
У одинаковых струн один и тот же тембр, поэтому звучат они неразличимо (унисон). При изучении модели «одинаковость» — вещь понятная и достижимая. Но в реальной музыкальной жизни у «одинаковых» струн частотные наборы совпадают, а громкости обертонов могут чуть-чуть отличаться. Следовательно, их тембры близки, но не совпадают. Совместное звучание таких инструментов тоже будет унисоном, но интереснее, чем у каждого из них в отдельности, тембр — богаче.
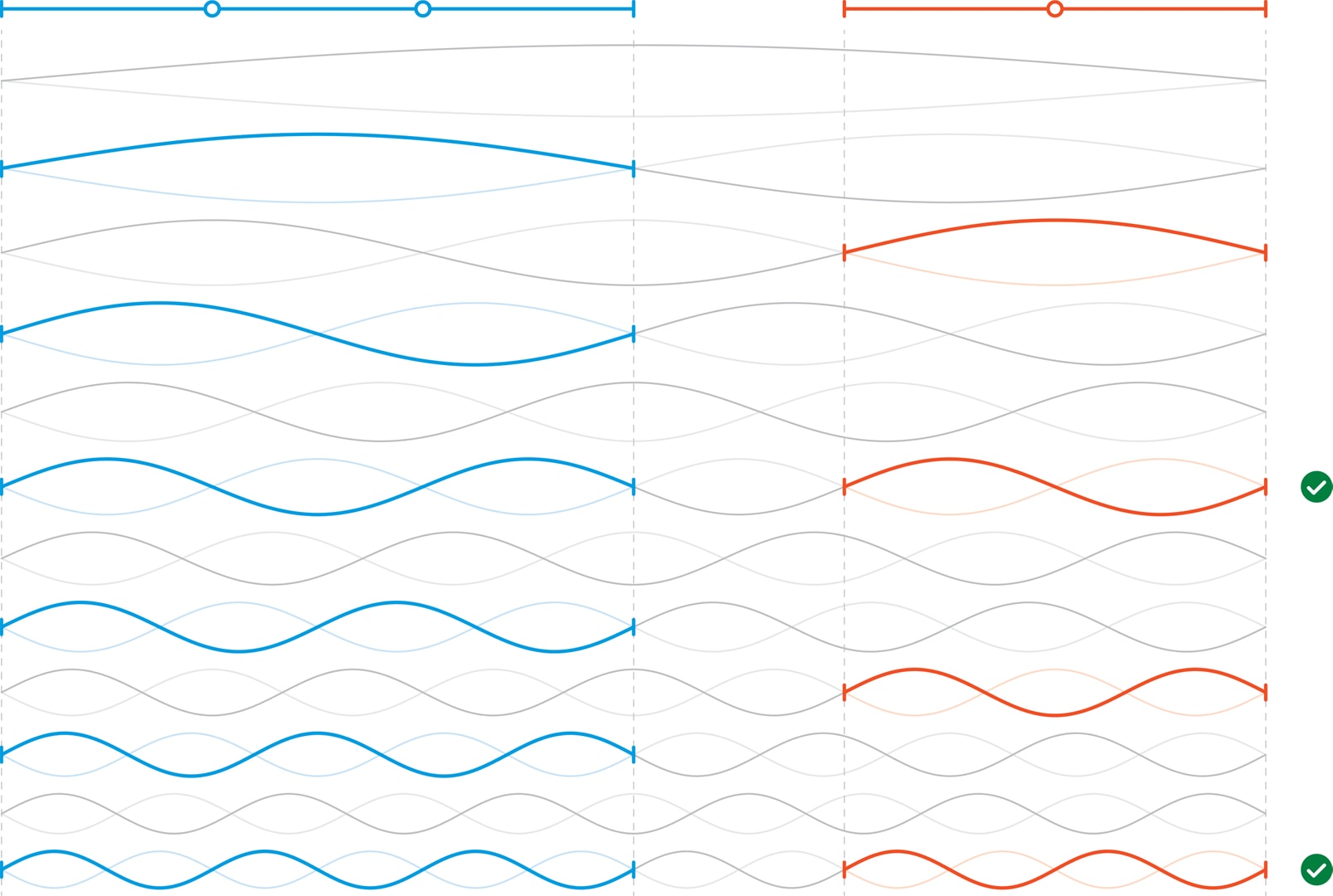
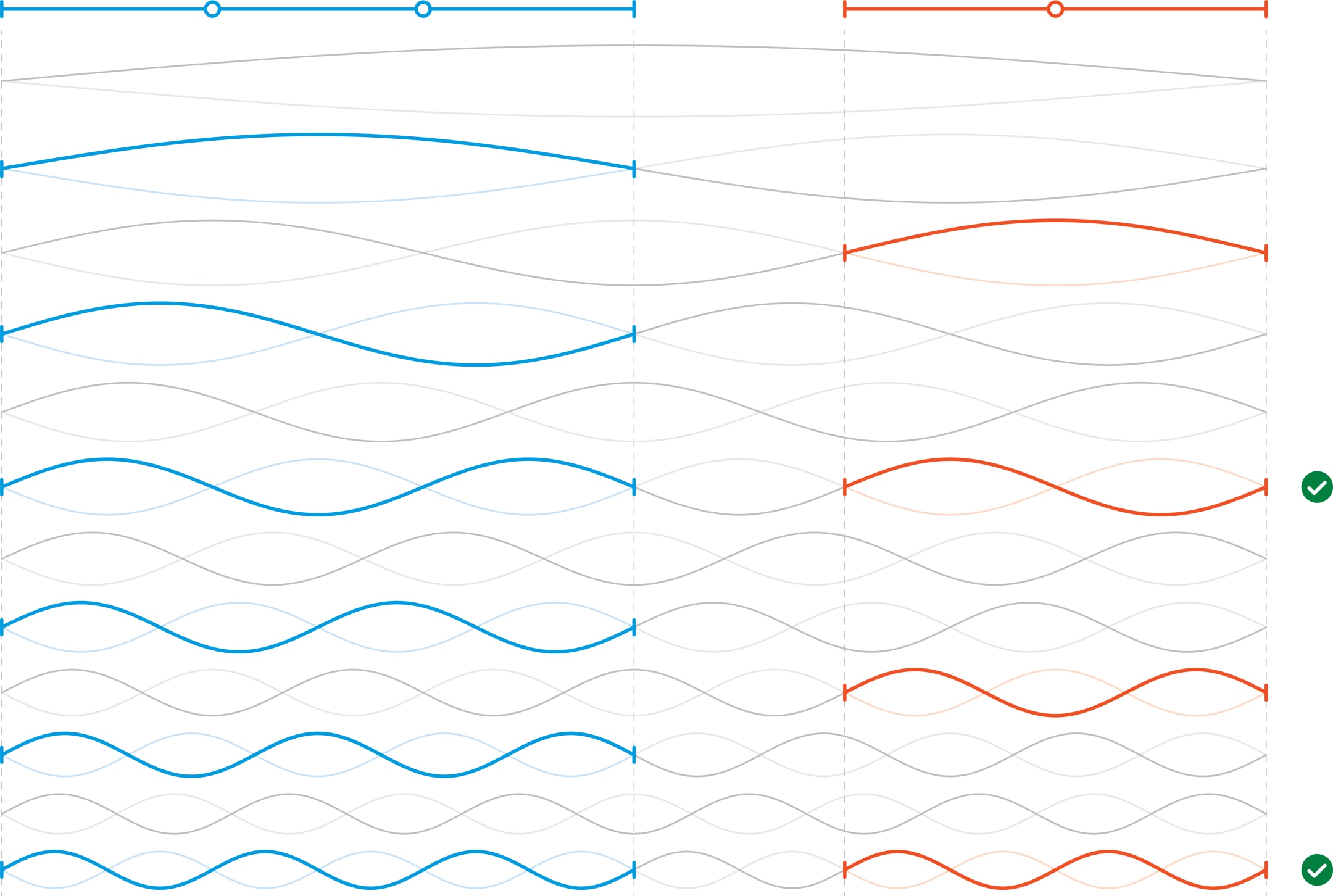
В октаве длины струн отличаются в два раза, и если набор частот у большей струны $\{f,\ 2f,\ 3f,\ 4f,\ …\}$, то у половинной струны — $\{2f,\ 4f,\ 6f,\ 8f,\ …\}$. Второй набор является частью первого, что объясняет согласованность звуков в октаве — они воспринимаются как похожие, хотя и отличаются по высоте.
В отличие от унисона, в октаве громкость (амплитуда) меняется только у «чётных» обертонов большей струны, а у её основного тона $\{f\}$ и «нечётных» обертонов $\{3f,\ 5f,\ 7f,\ …\}$ — не меняется.
Перейдём к квинте. Если $\{f,\ 2f,\ 3f,\ 4f,\ …\}$ — частотный набор струны длины $\ell$, то $\Bigl\{\frac{3}{2} f,\ 2\cdot\frac{3}{2} f,\ 3\cdot\frac{3}{2} f,\ …\Bigr\}$ — частоты струны длины $\frac{2}{3}\ell$. Видно, что даже основной тон малой струны $\frac{3}{2} f$ не входит в число обертонов большей струны. Следовательно, рассмотренный подход, объяснивший благозвучие октавы, непосредственно на квинту не переносится.
Но при восприятии звуков происходит их сопоставление, сравнение, в первую очередь — основных тонов. И возникает воображаемая «объединяющая» струна длины $2\ell$, в частотный набор которой $\Bigl\{\frac{f}{2},\ 2\cdot\frac{f}{2},\ 3\cdot\frac{f}{2},\ …\Bigr\}$ погружаются и основные тоны струн $\ell$ и $\frac{2}{3}\ell$, и даже все их обертоны.
Важно, что длина «объединяющей» струны — $2\ell$, что относительно близко к длинам струн квинты. Длина $2\ell$ — наименьшая, в которую целое число раз укладываются отрезки длины $\ell$ и длины $\frac{2}{3}\ell$, можно сказать, это их наименьшее общее кратное. Следствием близости числа $2\ell$ к $\ell$ и $\frac{2}{3}\ell$ является то, что основные тоны струн квинты оказываются обертонами струны $2\ell$ с небольшими номерами, т. е. являются благозвучными и «заметными» игроками в тембре объединяющей струны.
Включение частот обеих струн квинты в гармоничный мир обертонов объединяющей струны вызывает у слушателя ощущение благозвучности и согласованности.
С другой стороны, при восприятии звуков происходит и прямое сопоставление частот струн квинты: $\{f,\ 2f,\ 3f,\ 4f, …\}$ у струны $\ell$, $\Big\{\frac{3}{2} f,\ 2\cdot\frac{3}{2} f,\ 3\cdot\frac{3}{2} f,\ …\Big\}$ у струны $\frac{2}{3}\ell$.
Все «чётные» обертоны малой струны являются обертонами большей, а основной тон и все «нечётные» обертоны малой струны — нет. Эти «непарные» тоны малой струны — причина того, что гармония становится неполной: квинта благозвучна, но уступает октаве.
Анализ звучания кварты проводится аналогично. Для струн длиной $\ell$ и $\frac{3}{4}\ell$ длина объединяющей струны возрастёт и будет равна $3\ell$. Результат — кварта является чистым интервалом, но звучит менее гармонично, чем квинта.
Описание звука струны как композиции основного тона и обертонов математически означает представление периодической функции суммой гармоник $\sin nx$, $\cos nx$. Эта сумма может быть «внешне» совсем непохожей на гармоники-составляющие. Из простых по звучанию тонов складывается богатый, выразительный тембр звука.
Развитие идеи разбиения звука на гармоники (функции вида $\sin nx$, $\cos nx$) привело в XVIII веке к возникновению новой математической дисциплины — гармонического анализа. Для решения различных задач основным методом нахождения периодических решений стало разложение искомой функции в тригонометрический ряд.
В гармоническом анализе одно из базовых утверждений — то, что при разложении «хорошей» функции в тригонометрический ряд (называемый в этом случае рядом Фурье) в гармониках $a_n\cos nx + b_n\sin nx$ коэффициенты $a_n$ и $b_n$ стремятся к нулю при $n \to \infty$. Отмеченное уменьшение амплитуд (громкостей) у обертонов с ростом номера наглядно иллюстрирует приведённое утверждение, которое называется леммой Римана о коэффициентах Фурье.